流体阻力和抛射高度对抛射体运动规律的影响研究*

易 婉 周 琪

(湖南科技大学物理与电子科学学院 湖南 湘潭 411201)

陆振烟

(湖南科技大学物理与电子科学学院 湖南 湘潭 411201;智能传感器与新型传感材料湖南省重点实验室 湖南 湘潭 411201)

麻志君 周海霞

(湖南科技大学物理与电子科学学院 湖南 湘潭 411201)

在物理学中,抛体运动的相关研究是极为重要的内容,其中最简单也是最常见的模型为:不考虑流体阻力的影响,且抛出点与落地点处在同一水平线上,此时的抛体运动的轨迹是一条关于通过最高点的垂线左右对称的抛物线,最佳抛射角为45°[1],且该角度与抛体初速度和质量均无关.但当抛射点与落地点不在同一条水平线上时,抛体的最佳抛射角会随着抛射高度的增加而减小.在忽略空气阻力的前提下,文献[2]研究了运动员身高和手臂长度对铅球运动成绩的影响,结果表明运动员肩膀高度的差异对抛射速度的影响非常小,但对最大射程有一定影响,差别约为几十厘米,且肩膀高度越高,最佳抛射角越小而最大射程越大.在将理论计算结果与国内著名铅球运动员的比赛数据进行比较后,发现假若运动员的实际抛射角越接近理论预测的最佳抛射角,则射程越远,反之则射程越近.这表明理论计算结果的可信赖程度高.

自然界和军事活动中,常常能见到高速飞行的物体.而当流体密度比较大或飞行物体速度很大时,流体阻力对飞行物体的影响将变得不可忽略[3].在文献[4]中,考虑空气阻力与速度成正比的条件下,利用拉格朗日乘子法推导和研究了斜面上抛射物体运动规律,而文献[5-6]则考虑了空气阻力与速度的平方成正比情形下,通过 Matlab 数值求解其常微分方程,分析了射程、射高和飞行时间与初始角度之间的关系.但这些讨论仅局限于斜面抛体或抛出点和落地点在同一水平线上的情形,而且并没有将阻力、初速度、抛射高度对抛体运动的影响进行综合考虑.因此,本研究将从抛体动力学方程出发,推导一般情形下抛体运动轨迹方程,并进行数值计算和作图,从理论上探究阻力、初速度和抛射高度对抛体运动最佳抛射角的影响.

1 考虑阻力的抛体运动模型

我们假设抛体的质量为m,抛射速度为v0,抛射高度为L.如图1所示,建立直角坐标系xOy,质量为m的物体从原点O正上方L处以大小为v0的初速度抛出,初速度与x轴方向的夹角为θ,运动时间为t时的速度为v.当抛体轨迹与直线y=0相交时,交点与原点的水平距离即为抛体的射程,记为X.

在流体中运动的物体,其所受阻力通常与运动速度的幂次相关[7].为了简单起见,我们考虑阻力大小与抛体速度成正比关系[8-9],即

f=-kv

(1)

对于抛体运动,我们可以将运动分解为沿着x和y轴方向的变速直线运动.根据牛顿第二定律,考虑阻力的x和y方向的动力学方程为

(2)

当t=0时,有初始条件x=0,y=0,vx=v0cosθ,vy=v0sinθ.对式(2)进行分离变量,并结合初始条件积分得到抛体运动在x和y方向的速度大小为

(3)

进一步对式(3)进行积分,可得到物体在x和y两个方向的运动学方程为

(4)

再利用消元法消去时间t可求得抛体运动的轨迹方程为

(5)

假设物体落到水平地面的射程为X,由式(5)可知抛体射程X满足如下超越方程

(6)

很显然,无法从上述超越方程中直接反解出抛体射程的显式表达式.与文献[8]中采用近似法求解超越方程的解不一样,我们利用数学软件编写代码对其数值求解,并最终通过作图软件进行绘图,更加详细及直观展示阻力及抛射高度对抛体最佳抛射角的影响,具体数值计算结果将在下面进行详细展示和讨论.

2 数值计算结果及分析

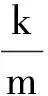
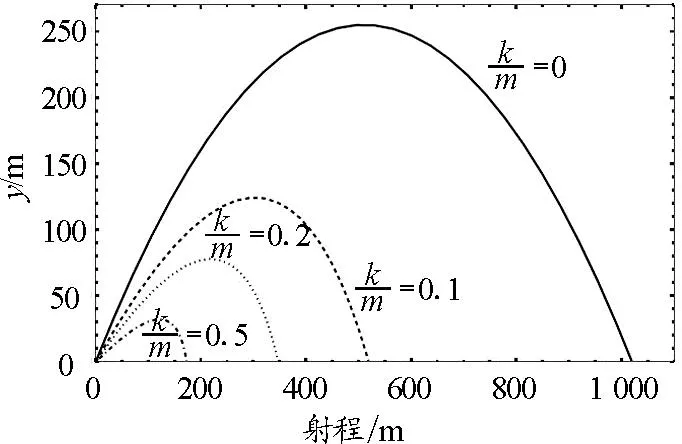
图2 抛体运动轨迹与流体阻力的关系

2.1 阻力及初速度对抛体最佳抛射角的影响

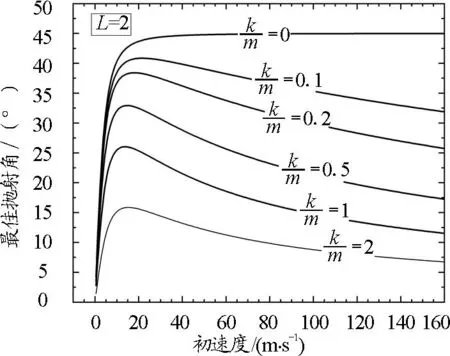
图3 抛射高度L=2 m时,最佳抛射角随初速度的变化关系

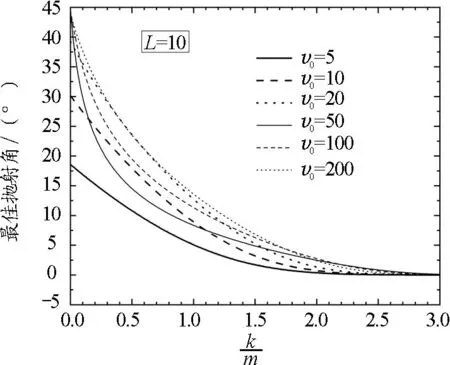
图4 抛射高度L=10 m时,最佳抛射角随阻力系数的变化关系

2.2 流体阻力、初速度及抛射高度对抛体最佳抛射角的影响

为了从多方面展示最佳抛射角随阻力系数的变化关系,我们在图5中描绘了初速度v0=100 m/s以及抛射高度L=2 m、5 m、10 m、20 m、50 m、100 m、200 m的条件下所得到的最佳抛射角与阻力系数的变化曲线.这几条单调下降的曲线表明最佳抛射角随空气阻力系数的增大而减小:当抛射高度较小时,其对应的最佳抛射角较大,并且曲线的下降相对而言也较为平缓;而当抛射高度较大时,曲线下降的速度更大一些,其中对应于L=100 m、200 m的两条曲线甚至几乎呈直线型下降.但无论抛射高度是大还是小,在抛射高度与初速度确定的情况下,最佳抛射角都是随着空气阻力系数的增大而减小,且变化趋势逐渐变得平稳,最后趋于一个稳定的值.

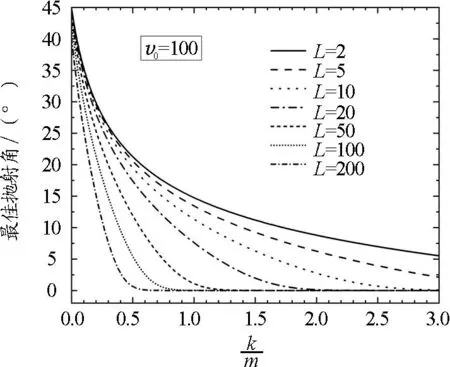
图5 初速度v0=100 m/s时,最佳抛射角随阻力系数的变化关系

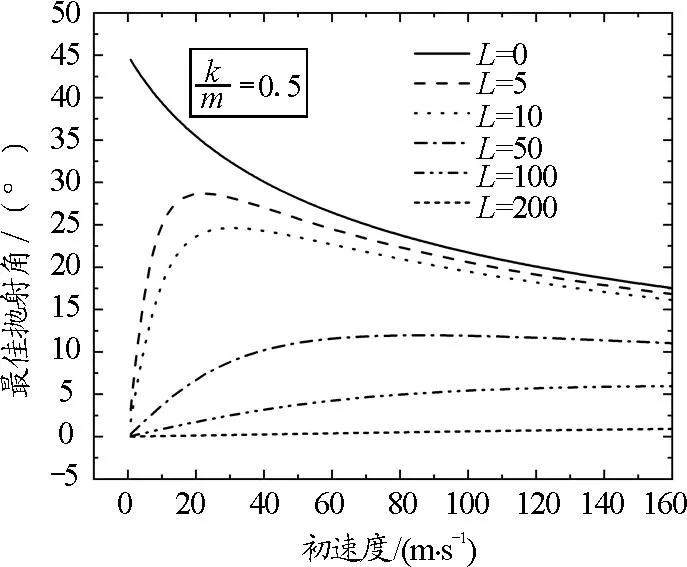
图6 阻力系数时,最佳抛射角随初速度的变化关系

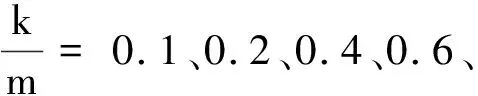
图7 初速度v0=100 m/s时,最佳抛射角随抛射高度的变化关系

3 结论

流体阻力对高速飞行物体的影响通常不可忽略.本文从抛体的动力学方程出发,推导考虑阻力和抛射高度影响下抛体运动的轨迹方程,借助数学软件进行数值计算和绘图,定量研究了阻力和抛射高度对抛体运动规律的影响,得出以下结论.