基于混合效应模型的林分优势木平均高-平均胸径模型研究

谢仕奎

凉山州仕汇林农发展规划有限公司, 四川 凉山 615000

树高与胸径是描述林木生长状况的主要调查因子，他们之间往往存在正相关的相关关系[1-3]。林分是指林木的内部结构特征[4]，林分优势木平均高是反映林分状态重要指标，他是最稳定的调查因子之一[5-6]。现地调查可以准确测量出林分优势木平均高，但相较于胸径，树高的测量难度更大[7]。通过胸径来推算树高在一定程度上为林业调查提供了便利[8-10]。

目前，多数树高—胸径模型的构建多是围绕林木开展[11-13]，以林分为研究对象的较少。树高胸径的相关关系在不同树种之间也会存在差异[14-16]。传统的回归模型在复杂的计算中不适用，林分优势木平均高—平均胸径之间的相关关系受多种因素的影响使其不再是一个简单的变化，使用传统回归模型来预测林分优势木平均高，其结果可能是有偏的[17-19]。随着数学、统计学软件的发展，混合效应模型逐渐被应用于林业领域[20-21]，混合效应模型应用于重复测量数据时，在考虑固定效应的同时考虑了随机效应，不仅能描述数据整体的变化规律，还能反映数据之间的变化，估计结果时更为准确[22]。

通过会理市“二调”数据分析，选择树种面积占木材树种面积之比最多的5 个乔木树种（云南松54.0%，其他硬阔12.2%，桤木11.6%，栎类6.5%，华山松3.3%）为研究对象，布设123 块样地，通过模型拟合来研究林分优势木平均高—平均胸径的相关关系，以期为类似林分的优势木平均高的估算提供参考。

1 研究区概况及数据来源

1.1 研究区概况

研究区位于会理市，东经101°52′～102°38′，北纬26°5′～27°12′，属中亚热带西部半湿润气候区，阳光照射充足，年均日照2400h，年均气温15.1℃，有丰富的光热资源，蒸发旺盛；雨量集中，干湿季分明；气温年较差小，日较差大；冬暖无严寒，夏凉无酷暑；气候垂直变化大，高山积雪、峡谷炎热；气温回升和下降波动大。

1.2 数据来源

5 个主要树种分布范围内布设实测样地，样地为方形，面积666.7m2（见图1），各样地点位基本信息见表1，林分优势木平均高（算术平均高）和平均胸径（算术平均胸径）因子统计结果见表2。

表1 各样地基本信息一览表Tab. 1 Basic information of various sample plots

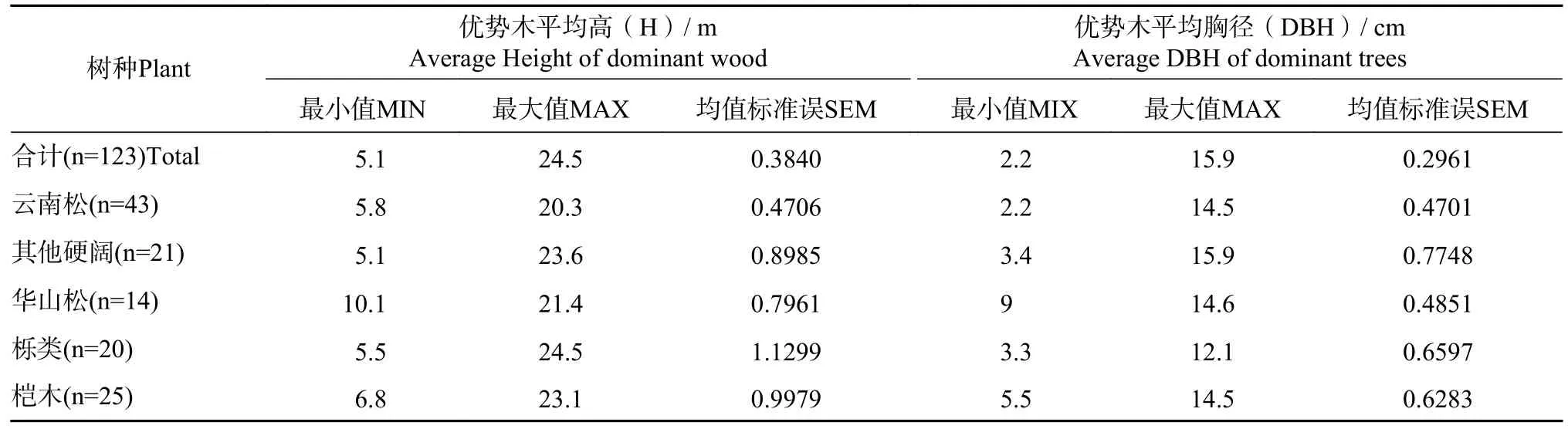
表2 各树种调查因子统计一览表Tab. 2 Statistical investigation results of various tree species

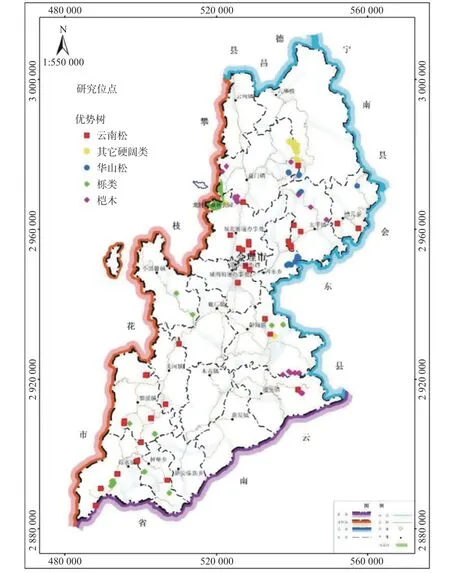
图1 样地布设位置示意图Fig. 1 Schematic diagram of sample plots layout position

2 研究方法

2.1 林分优势木平均高—平均胸径模型构建

采用常见的5 个函数模型，通过IBM SPSS Statistics 的曲线估计来构建林分优势木平均高—平均胸径模型，各模型表达式如下：

线性：H=β1×DBH

二次函数：H=β1×DBH2+β2×DBH

三次函数：

幂函数:H=DBHβ1

对数函数：H=β1×lnDBH

式中：H为林分优势木平均高、DBH为林分优势木平均胸径，β1、β2、β3为估计参数。

模型评估通过决定系数R2进行评价。R2越大，模型拟合效果越好。

式中：Hi为林分优势木平均高实际值，分别为预测值和平均值。

2.2 林分优势木平均高—平均胸径混合效应模型构建

以全部样地为研究对象，分别以线性、对数函数、二次函数、三次函数、幂函数来构建林分优势木平均高—平均胸径模型，选择决定系数最高的模型作为基础模型，加入随机效应参数，构建林分优势木平均高—平均胸径混合效应模型。

混合效应模型的拟合精度以赤池信息准则AIC、贝叶斯信息准则BIC两个指标进行评价。

3 结果分析

3.1 林分优势木平均高—平均胸径模型构建

从表3 可以看出，从不同函数来看，5 个函数模型均能较好地拟合林分优势木平均高—平均胸径模型，各树种拟合的R2均在0.879 以上，幂函数模型表现最好。对数函数、线性函数在拟合林分优势木平均高—平均胸径时表现较差；从不同树种来看，华山松林分优势木平均高—平均胸径模型拟合精度最高，其中，华山松林分幂函数模型的R2最高，达0.997，栎类林分优势木平均高—平均胸径模型拟合精度最低，其中栎类林分对数模型的R2最低，仅有0.879。各树种林分优势木平均高与平均胸径的相关关系均为极显著，最优模型拟合结果见表4。

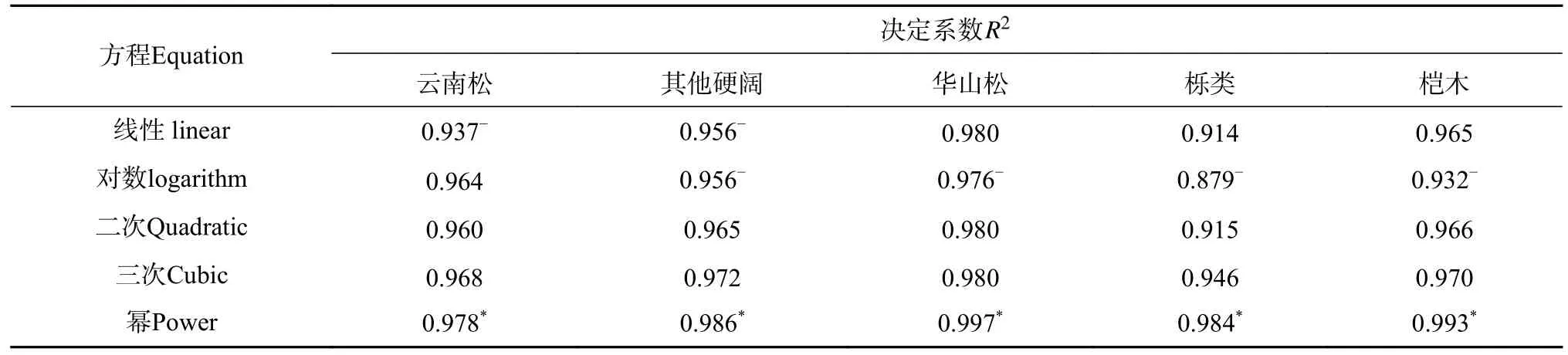
表3 林分优势木平均高—平均胸径拟合结果Tab. 3 Fitting results of average height and average DBH model of dominant trees in forest stands

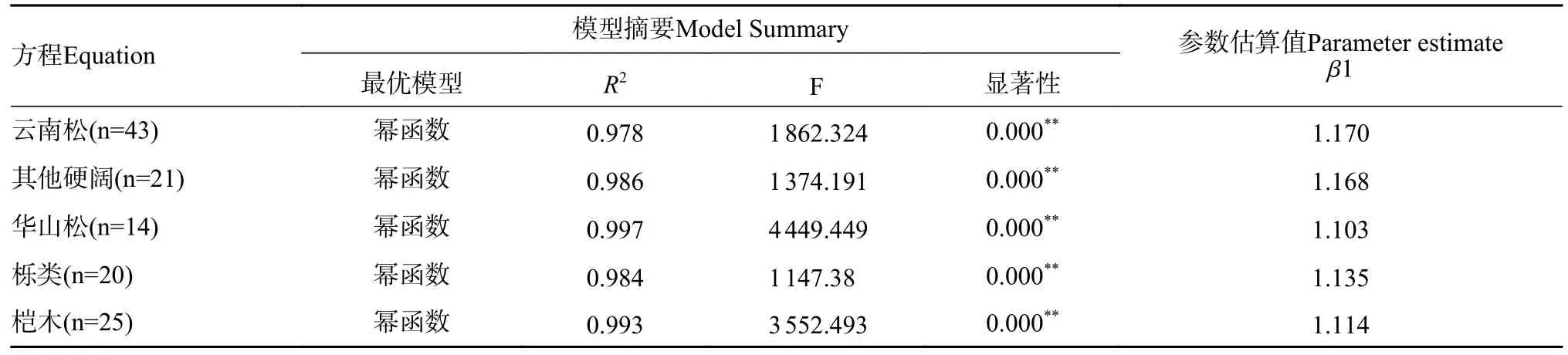
表4 各树种最优林分优势木平均高—平均胸径模型Tab. 4 Average height and average DBH model of dominant trees in the best stands of each tree species

3.2 林分优势木平均高—平均胸径线性混合效应模型构建

（1）基础模型选型

从表5 可以看出，幂函数模型的R2最高，拟合效果最好，故选择幂函数模型作为基础模型来构建混合效应模型。

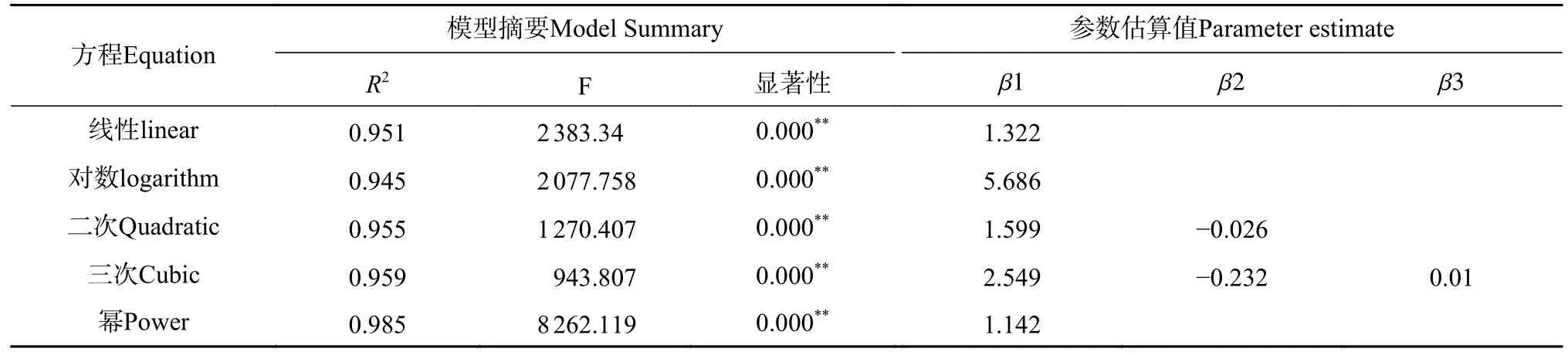
表5 林分优势木平均高—平均胸径模型的参数估计及模型评价Tab. 5 Parameter estimation and model evaluation of average height and average DBH of dominant trees in forest stands

（2）混合效应模型构建

从表6 可以看出，将参数 β1作为混合参数时，AIC 、BIC大于不考虑混合参数的基本模型，即将β1作为混合参数不能提高模型的拟合精度。将 β2作为混合参数，或者将β1、β2同时作为混合参数时，AIC 、BIC均小于不考虑混合参数的基本模型，模型拟合效果更好。在考虑随机效应的混合效应模型中，参数 β2作为混合参数时，模型的拟合效果最好。则混合效应模型 表达式如下：

表6 林分优势木平均高—平均胸径混合效应模型评价Tab. 6 Evaluation of Mixed Effect Model of average height and average DBH of dominant trees in forest stands

混合模型:H=DBHβ1+β2′

式中：H为林分优势木s、DBH为林分优势木平均胸径， β1为固定效应参数， β2’为包含截距随机效应的混合参数。

（3）混合效应模型优化

混合效应模型考虑不同的协方差结构，可以提高模型的拟合精度，选用方差成分、对角以及复合对称来考虑模型的协方差结构来优化混合效模型，从表7 可以看出，使用复合对称的方差结构来参与模型拟合，AIC 、BIC最小，模型效果最优。最优模型拟合结果见表8。

表7 林分优势木平均高—平均胸径混合效应模型评价Tab. 7 Evaluation of Mixed Effect Model of average height and average DBH of dominant trees in forest stands

表8 林分优势木平均高—平均胸径混合效应模型拟合结果Tab. 8 Fitting results of Mixed Effect Model of average height and average DBH of dominant trees in forest stands

基础模型与最优混合模型预测—实测散点图详见图2，从图2 可以明显看出，最优混合模型考虑了截距 β2’作为混合参数来参与模型拟合。

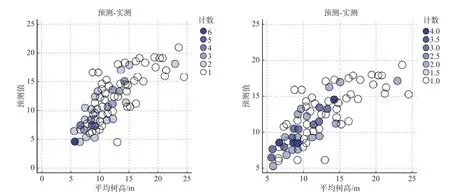
图2 基础模型（左）与最优混合模型（右）预测—实测散点图Fig. 2 Basic model (left) and optimal mixed model (right) prediction - measured scatter plot

4 讨论

李明华等使用模型法来研究上海市主要造林树种胸径与树高之间的变化关系，各模型的拟合效果均较好[23]。刘浩等以18 块落叶松人工林为研究对象，使用6 个方程来拟合树高—胸径模型，各方程的R2均在0.81 以上[24]。多位学者的研究均表明树高与胸径的相关关系极显著，与本次研究结果一致。许多学者研究树高—胸径模型均得出相同的结论：幂函数模型的拟合效果最好[25-26]，本次研究也是幂函数模型的拟合精度最高，其中，华山松林分的幂函数模型拟合精度最高，达到了0.997。栎类对数函数模型的拟合精度最低，仅有0.879。华山松样地为人工，海拔跨度353 m，在研究的5 个树种中海拔跨度最小，郁闭度跨度也较小，而栎类林分起源为天然，海拔跨度最大，达到1 379 m，这些环境因素应该对模型拟合精度产生了一定的影响。刘春云等学者研究中国落叶松林胸径与树高的相关关系时发现胸径与树高受温度的影响极显著，不同的环境因子均能对树高胸径的相关关系产生影响[27]。混合模型应用于木材碳密度变化时表现出更好适用性[28]，混合效应模型在研究林分平均高与林分优势木平均高的相关性上不仅反映了其整体变化趋势，还能体现立地条件之间的差异。模型拟合效果更好[29]，多数关于树高与胸径之间的相关关系研究都是针对单一树种，此次研究考虑林分优势木平均高与平均胸径的相关关系时，将不同树种作为一个整体，考虑树种之间的差异作为随机效应参与模型拟合，混合模型的AIC 、BIC的表现更优，模型拟合效果更好，说明在类似林分条件下混合模型不仅可以反映林分优势木平均高在平均胸径上的整体变化趋势，还能体现不同树种对其产生的影响。