面向车辆与参数服务器双向选择的联邦学习算法
庄 琲,韩志博,聂锦标,李子怡,林尚静
(北京邮电大学 安全生产智能监控北京市重点实验室,北京 100876)
0 引言
近年来,基于人工智能的模型训练方法主要使用传统的基于云的集中式学习框架。然而,这种将训练数据传输到云服务器进行处理的方法存在一系列问题,包括传输质量、数据隐私和高消耗[1]。因此,领域内提出了边缘计算来改善这些问题,并将数据处理和其他任务放在离设备更近的边缘服务器上。联邦学习[2]作为一种分布式框架,促进了边缘计算的发展。它允许用户在本地保存数据,边缘服务器作为参数服务器,将训练模型参数上传到参数服务器进行参数融合。目前,联邦学习已广泛应用于物联网,如入侵检测[3]、网络流量分类[4]和自动驾驶汽车[5]。车联网作为特殊的物联网场景,也逐渐得到关注,车辆可以通过车对基础设施技术(Vehicle-to-Infrastructure,V2I)[6]与路边单元、基站等基础设施进行数据交换。联邦学习应用在车联网中,保护车辆用户个性化隐私数据的同时,可以避免将大量训练数据上传至云服务器,提高了通信效率。
在车联网场景下,拥有云服务器的服务提供商为车辆提供车载娱乐、自动驾驶和路径规划等服务[7-8],需要利用车辆的私有数据进行联邦学习共同训练一个机器学习模型,再部署到车辆上为其提供服务。
车联网下的联邦学习面临许多挑战:
一方面,由于车辆设备的异构性,联邦学习参与者的设备条件参差不齐,容易造成通信和计算效率低下、资源浪费的问题。现有文献主要考虑到车辆自身条件以及信道条件等因素进行车辆节点选择,Wang等人[9]提出了一种基于数据集内容的车辆选择和资源分配方案,提高了模型精度与收敛速度。文献[10]提出了基于内容均衡性的车辆选择方法,综合考虑了车辆本身数据集内容分布不均衡、车辆计算能力以及无线信道的影响。文献[11]设计了一种分布式数据流抽样算法来进行车节点选择,能够保证车节点最大可能地参与模型训练。文献[12]提出了一种基于链路时长预测的联邦训练节点选择机制。该机制首先根据车辆上传的相关指标预测出边缘节点与车辆剩余的通信时长,将其与模型训练时长综合考虑来决定车辆是否参与训练。Saputra等人[13-14]在联邦学习的每一轮中,根据车辆的当前位置来进行车辆选择,确定联邦学习过程中的一组最佳车辆集合。其中,文献[14]更进一步考虑了车辆的信息历史的影响。Yu等人[15]提出了一种基于近端策略优化(Proximal Policy Optimization, PPO)的用户选择方法,综合考虑了用户本地数据质量、能耗和通信延迟,解决了车联网中联邦学习的用户选择问题。Lu等人[16]将车辆节点选择建模为一个时间成本的优化问题,采用深度强化学习求解,提高了联邦学习效率。尽管有研究将车辆位置考虑进车辆选择,但车辆位置是快速实时变化的,算法需要捕捉移动性带来的长期影响,且全面考虑设备的通信与计算条件。
另一方面,大量车辆参与联邦学习,短时间内与参数服务器频繁通信,高并发的访问会造成通信拥塞,进一步导致训练瓶颈。为了实现负载均衡,车辆可以切换接入的参数服务器,选择最优的参数服务器上传梯度数据。 演化博弈是解决用户选择行为动力学的一个有效工具。演化博弈与传统的博弈论不同,它不要求参与者完全理性。Fan等人[17]在空天地一体化网络场景下引入演化博弈理论研究用户的动态网络选择行为和演化均衡。Luong等人[18]在智能反射面辅助无线网络场景下,采用演化博弈分析用户的服务提供商和服务选择行为。Van等人[19]在基于6G的支持速率分割多址的网络中,利用演化博弈解决移动用户的动态网络资源选择问题。赖成喆等人[20]在车联网下应用演化博弈解决车辆是否参与数据包转发的问题,证明演化博弈在车联网下具有优势:由于车辆的移动性,车辆节点通信链路不一定稳定且完整,车辆为有限理性状态,演化博弈对车辆行为建模,车辆节点会动态根据网络状况调节自身策略实现利益最大化。进一步,由于网络环境是动态的,文献[21]采用基于演化博弈和双层博弈的车载异构网络选择方法解决了动态网络环境中异构网络切换时出现的大规模乒乓效应。现有研究对参数服务器的选择问题关注较少,车联网中,大量的车辆接入参数服务器,会导致通信拥塞,在联邦学习场景下,也面临着模型准确度与训练成本之间的权衡。
针对上述问题,提出一种考虑移动性和资源的基于模糊逻辑的车辆选择方案和基于演化博弈的参数服务器选择方法。在大量移动车辆场景下,选择计算能力强、数据量多的车辆参与训练,降低移动车辆对全局模型准确度产生的影响,采用演化博弈对车辆自主选择参数服务器的过程建模,通过复制者动态刻画车辆决策的动态性和有限理性,解决易产生通信拥塞的问题,降低通信和计算成本。
1 系统模型
车联网中,云服务提供商通过边缘服务器向底层的车辆用户发布计算任务,通过联邦学习协同训练特定的智能模型,如图1所示。

图1 车联网下的联邦学习框架Fig.1 Federated learning framework for internet of vehicles
车联网下的联邦学习框架主要包括任务发布者层、边缘层和用户层。边缘层由多个边缘服务器组成,例如基站和路边单元,由边缘服务器调动大量车辆用户参与联邦学习。
为了提高通信效率,推动联邦学习有效进行,本文提出了一个移动感知的高效分布式系统模型,即基于模糊逻辑的车辆选择和基于演化博弈的参数服务器选择方法,如图2所示。
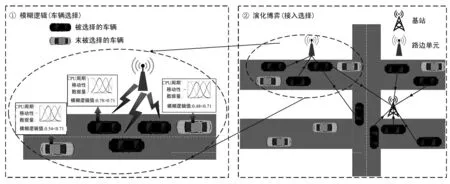
图2 移动感知的高效分布式系统模型Fig.2 Efficient distributed System model for mobile sensing
1.1 联邦学习

ωi(t)=argminFi(ω),
(1)
式中:Fi(ω)表示车辆i的损失函数,本文采用交叉熵损失函数作为车辆本地训练模型的损失函数。损失函数的反向传播是机器学习训练过程中调整权重和参数的必要条件。第i辆车在t轮迭代中更新参数的过程如下:
ωi(t)=ωi(t-1)-η∇Fi(ωi(t-1)),
(2)
式中:η为学习率,η∈[0,1]。在每一轮全局迭代后,车辆将训练的本地模型上传至参数服务器。
全局模型更新:在每一轮全局迭代后,参数服务器接收到来自所有车辆的本地模型,并进行全局模型更新。模型参数更新算法可以选择联邦平均算法、联邦加权平均算法和联邦随机梯度下降算法等方法。由于模型参数更新算法不是本文的研究重点,所以选取基础的联邦平均算法进行全局模型的更新。因此,在t轮迭代中全局模型的更新过程为:
(3)
式中:D为联邦训练的总数据量大小。将更新后的全局模型参数下发到所有车辆,车辆在该全局模型的基础上开始下一轮迭代训练,重复迭代过程,直至达到最大迭代次数或全局模型收敛。
1.2 模糊逻辑法

1.3 演化博弈
在通过模糊逻辑法选出参与联邦学习的车辆后,为了实现进行联邦学习时参数服务器的负载均衡,采用演化博弈推动车辆自主选择最优的参数服务器。在博弈过程中,用户需要贡献自己的数据并消耗自己的资源,而参数服务器需要动员更多的车辆加入协同训练模型,从而提升模型训练准确度。初始所有车辆随机选择一个参数服务器加入,并计算当前选择策略能够获得的收益。在每一轮迭代后,车辆都会调整他们的策略,倾向于加入能够获得更高收益的参数服务器。
在传统博弈理论中,假设参与者是完全理性的,且博弈在完全信息条件下进行。但在现实中,参与者的完全理性与完全信息的条件是很难实现的,且参与者之间具有差异性。与传统博弈理论不同,演化博弈理论不要求参与者是完全理性的,也不要求完全信息的条件。演化博弈所刻画的是具有有限理性的群体通过各种具体的动态学习模仿行为,最终达到稳定均衡状态的过程。
2 算法设计
先通过模糊逻辑法选择参与联邦学习的车辆,再采用演化博弈建模被选择的车辆动态选择参数服务器的过程。
2.1 基于模糊逻辑的车辆选择
在车辆的选择中考虑了三个因素:车辆的设备条件、数据量和移动性,分别用车辆计算的CPU周期频率、车辆本地私有数据量大小和车辆速度数据来衡量。设备条件因素确保了总是可以选择计算能力更强的车辆,降低训练时的计算时延;数据量因素确保了所选车辆具有更大的数据量,有利于提高模型训练的准确度;考虑移动性因子可以尽可能选择速度接近全体车辆平均车速的车辆,确保车辆之间的通信连接更稳定。由于车辆的移动性,车辆获取的信息往往不完整或不精确,因此采用模糊逻辑来进行车辆选择,使用了较为主观的模糊规则,具有鲁棒性和较强的容错能力。
2.1.1 模糊逻辑因素
计算三个模糊逻辑因素的影响因子值,分别用来代表车辆的设备条件水平、数据量大小和移动稳定性。
① 设备条件因素:采用车辆的CPU周期频率值来衡量车辆的计算能力,对车辆的CPU周期频率进行归一化处理得到设备条件影响因子值。
(4)
式中:车辆i的CPU周期频率记为fi,CFi表示车辆算力相对大小,CFi的值越大,代表车辆i的计算能力越强。CFi值较大的车辆更有可能被选择,因其拥有更丰富的计算资源,可以减少联邦学习时的计算时延。
② 数据量因素:对车辆本地私有数据量大小进行归一化处理得到数据量影响因子值。
(5)
式中:车辆本地拥有的私有数据量大小为Di,DFi表示车辆拥有数据量的相对大小。DFi值越大,代表车辆i的拥有的数据量越多。由于联邦学习时大量的训练数据有利于提高训练模型的准确度,倾向于选择DFi值较大的车辆。
③ 移动性因素:主要采用车辆的速度值来衡量车辆的移动水平。车辆的移动性影响因子值计算如下:
(6)

2.1.2 隶属度函数
转化后得到的设备条件影响因子值、数据量影响因子值和移动性影响因子值为数字格式,本节通过隶属度函数转化为模糊数据,以便描述对车辆评价的高低,三个影响因子值的隶属度函数如图3所示。

(a) 设备条件因素

(c) 移动性因素

2.1.3 模糊规则
在将输入模糊化后,需要定义一组规则,来确定输入模糊变量和输出模糊变量之间的关系,定义的模糊规则如表1所示。

表1 模糊规则
在得到输出模糊变量后,需要通过解模糊化方法将其模糊格式重新转化为数字格式,以此来表示车辆属性的优劣,从而做出车辆选择决策。采用重心法进行解模糊化,通过输出隶属度函数得到输出变量具体的数值,输出隶属度函数如图4所示。定义阈值STh,将车辆的输出变量与阈值STh比较,若大于阈值则该车辆会被选为联邦学习的参与车辆。STh的大小可根据实际场景需求进行调整,从而控制参与车辆的数量和质量。
由于车辆环境是动态的,并且在每辆车上获取的信息是不完整或不精确的,因此很难使用简单的数学模型来解决车辆选择问题。车辆的选择过程考虑三个因素,即移动性因素、设备条件因素和数据量因素,每个因素对系统性能的影响也取决于其他因素的值。如果某个车辆一个因素的值很低,那么无论其他两个因素如何,选择该车辆的可能性都不高。所提出的基于模糊逻辑的方法能够根据定义的模糊隶属度函数和模糊规则来联合考虑这三个因素。当输入不精确或矛盾时,模糊逻辑可以做出很好的决策,从而为问题提供灵活的解决方案。
2.2 基于演化博弈的参数服务器选择
针对本文的场景,将车辆进行联邦训练时选择参数服务器的动态过程建模为演化博弈。
2.2.1 演化博弈要素
演化博弈包含四个基本要素:种群、适应度函数、动态和均衡。

② 适应度函数:适应度函数是指选择接入不同参数服务器的车辆所获得的收益。这与车辆所选择的参数服务器和当前的策略分布有关。将适应度函数定义为接入参数服务器所获得的奖励与通信、计算所产生的成本之间的差值。适应度函数的设计在下节进行了进一步的讨论。

④ 均衡:演化博弈的结果是达到一个收敛的稳定状态,即选择每个参数服务器的车辆比例收敛到一个唯一且稳定的点,最终车辆种群的策略分布向量表示为x*=(x1*,x2*,…,xM*)。
2.2.2 动态过程建模
本节详细描述定义的适应度函数。在参与联邦训练时完成一次迭代后选择接入参数服务器j的车辆群体的适应度为:
(7)

在使用分布式模型训练时,车辆越多,数据越多,模型准确度越高。拟合出数据量和全局模型准确度的关系[22]如图5所示,横坐标代表参与联邦训练的图片数,纵坐标代表联邦学习全局模型的准确度,每个数据点为联邦训练100次得到的均值,车辆在私有数据集上的本地训练轮数epoch设置为30,一次训练所选取的样本数Batch Size为128。

图5 数据量与模型准确度的关系Fig.5 Relationship between data size and model accuracy
所拟合的关系式表达如下:
Rj=0.057 1lg(D)+0.746 8,
(8)
式中:D为联邦训练的总数据量大小。
在每轮迭代结束后和下一轮迭代开始前,车辆与参数服务器之间进行参数交互,本文采用所交互的参数量作为一次迭代产生的通信开销,针对参数服务器j,其通信开销为所有与其交互的参数量总和。则参数服务器j一次迭代产生的通信成本表示如下:
(9)
式中:T为一次迭代交互参数的次数,一般情况下T=2,表示在每轮迭代结束后车辆向参数服务器上传一次本地模型参数,在下一轮迭代开始前车辆从参数服务器下载一次全局模型参数;|ω|为模型参数的大小,由于所有车辆本地所采用的机器学习模型结构相同,所有车辆交互的参数大小也近似相等。
在联邦学习的计算阶段,每个车辆在本地数据Di上训练本地模型。选择参数服务器j的所有车辆一次迭代产生的计算成本表示如下:
(10)
式中:εi为车辆i处理一单位数据所需的CPU周期数,fi为车辆i的CPU周期频率。
更进一步可得所有车辆在第t轮的平均适应度为:
(11)
在博弈过程中,车辆可以交换通过接入不同的参数服务器获得的适应度值信息,即净收入信息,从而与当前参数服务器进行比较。相比之下,车辆更倾向于加入能提供更高净利润的参数服务器。本文采用复制者动态去捕捉和建模车辆选择参数服务器的动态过程。
(12)
式中:α为车辆的学习率,控制车辆适应策略的速度。当种群规模较大时,车辆往往需要更多的时间来获得和传递信息和状态,学习速度往往较慢,α值设置得更小。

车辆之间的博弈最终会演化到一个唯一且稳定的均衡点,即种群从任何初始策略分布开始演化都可以收敛到相同的平衡点,且不再改变。
2.2.3 算法过程实现
上节对车辆进行了动态博弈过程的建模,本节对车辆动态演化博弈算法进行具体的阐述。不同于传统的演化博弈,由于车辆有限的规模,实际车联网下种群的策略分布是离散状态。
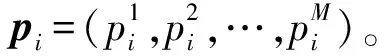
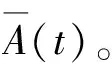
(13)
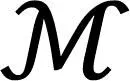
(14)

在策略分布收敛且所有车辆的策略概率分布向量收敛后,得到最终的策略分布x*=(x1*,x2*,…,xM*)。算法1给出了车辆动态演化博弈算法的伪码。

算法1 车辆动态演化博弈输入:车辆集合,策略集合,初始策略分布x(0)输出:演化博弈达到均衡时,种群的策略分布向量x∗1.t=0,车辆根据初始策略分布x(0)随机选择参数服务器2.WHILE ∀j∈,Aj(xj(t))-A(t) 考虑一个具体的城市街道车辆环境,由两个参数服务器和若干车辆构成,参数服务器分别为路边单元和基站。路边单元可以通过短距离直接通信接口PC5汇集道路上行驶车辆的信息,上传至V2X(Vehicle to Everything)平台,经过计算后将消息广播至车辆,通信覆盖范围设置为600 m。基站可以通过通信接口Uu实现与车的更大范围的长距离可靠通信,可以收集车辆信息同时具备计算能力,以4G基站为例,通信覆盖范围设置为2 000 m。在实验分析中,用A替代基站,B替代路边单元,假设所有车辆都在A和B的通信覆盖范围内,则有A和B两个参数服务器选择,分别对应车辆的A策略和B策略。 车辆之间的演化博弈过程建立在车辆进行联邦学习的背景下,考虑车辆训练MNIST图像数据集,采用卷积神经网络(Convolutional Neural Network,CNN)对图像数据分类和预测,模拟车联网的目标识别场景。以1∶1为所有车辆分配200或400张不同图片作为训练集,测试集是相同的1 000张图片。仿真设置车辆总数大于50,模拟高密度车辆环境,所采用的车辆CPU周期ε为5,CNN模型参数|ω|为0.02 MByte。实验环境使用Python 3.7.0利用 pytorch深度学习框架构建。在车辆动态演化博弈算法中所设定的阈值Th=0.001。 将演化博弈算法与其他算法获得的收益进行对比,对比算法包括K-means算法[23]和谱聚类算法[24]。K-means算法和谱聚类算法是分簇算法,谱聚类相比传统的K-means算法,对数据分布的适应性更强、计算量更小。采用这两种分簇算法按照车辆位置将车辆划分为两簇,分别接入A和B两个参数服务器。在进行算法对比时,随机在参数服务器通信范围内生成车辆位置,分别模拟50、75、100辆车的场景。 图6给出了在不同的初始策略分布下,B策略分布的演化最终收敛到纳什均衡点的过程。给定种群选择B策略的初始比例分别为0.2、0.3、0.4,种群中的车辆不断改变自身的策略选择,最终趋于稳定,选择最有利于自己的策略。可以看出,不同初始比例下最终都收敛到相同的平稳点0.44,则对应地选择A策略的种群比例为0.56。 图6 不同初始比例时B策略分布变化Fig.6 Changes in the distribution of strategy B at different initial proportion 图7分析了不同的车辆密度下的策略分布变化。在同一初始比例下,给出了50、75、100辆车的情境下,演化博弈的收敛过程,分别在第6、第22和第53次迭代时收敛。可以看出,无论何种车辆密度,演化博弈最终都可以达到收敛,参与的车辆数量越多,收敛的速度越慢。另外,不同数目的参与车辆最终的收敛点也不相同。由此可得,车辆越多,车辆需要更多的时间去适应策略,且演化博弈适用于大量车辆场景,在不同种群规模下都能达到稳定状态,个体都可以学习到最佳策略。 (a) 50辆车 (c) 100辆车 图8给出了相同初始条件下,设定不同的学习率α值时车辆选择不同策略的概率变化,体现学习率对演化博弈达到稳定需要迭代次数的影响。可以看出,学习率α越大,选择A、B策略的概率收敛越快,即种群适应策略的速度越快,且最终收敛值为0或1,验证了演化博弈算法的准确性。 图8 不同学习率时车辆选择不同策略的概率变化Fig.8 Probability variation of vehicle selecting different strategies under different learning rates 模型准确度反映了车辆选择A和B可以获得的利润,通信量反映了车辆接入A和B的通信拥塞程度,模型准确度与通信量的差值则反映了车辆的净收益。图9给出了不同车辆密度下车辆选择A和B对应的三个指标的变化。可以看出,随着车辆数的增加,通信量增加即通信拥塞程度上升,而模型准确度提高是由于训练数据的增加。收益在逐渐降低,这是因为随着车辆的增多,准确度提高速度比通信量增加速度慢。因此在实际应用中,应根据对准确度和通信开销的需求和容忍程度来选择参与训练的车辆数。 图9 不同车辆数适应度、准确度和通信量的变化Fig.9 Changes in fitness, accuracy, and communication cost of different number of vehicles 图10给出了在不同车辆数下,不同算法的总收益对比,选择不同策略的收益根据式(7)计算得出,求和得到总收益。 图10 不同车辆数下不同算法的收益对比Fig.10 Comparison of benefits of different algorithms under different number of vehicles 与K-means算法、谱聚类算法相比,采用演化博弈算法得到的总收益更高。当车辆数为50时,演化博弈与K-means算法、谱聚类算法的差距并不明显;当车辆数为100时,演化博弈相比其他算法收益明显更高。由此可得,随着车辆数的增加,演化博弈的效果更加显著,这恰恰证明了所提出的演化博弈理论的有效性。K-means和谱聚类算法由于在聚类时没有考虑准确度和通信计算成本,仅考虑车辆的位置因素,导致无法平衡准确度和通信计算成本,最大化车辆和整体利益。 提出了面向车辆与参数服务器双向选择的联邦学习算法,针对参数服务器调动大量车辆进行联邦学习时通信效率低下的问题设计算法。设计基于模糊逻辑的车辆选择算法,解决了车辆移动条件下通信连接不稳定以及车辆设备条件和数据量参差不齐的问题,设计较为主观的模糊规则,便于实际场景中根据具体需求更改车辆选择规则。此外由于车辆移动下通信质量较差,从车辆获取到的信息可能不完整或者不精确,模糊逻辑算法的容错能力可以弥补这一缺陷。进一步提出基于演化博弈的参数服务器选择算法,设计收益函数来平衡联邦学习模型准确度和通信与计算成本,利用复制者动态理论对车辆的动态自主决策过程建模,体现出车辆具有有限理性的特点,解决通信拥塞问题,同时最大化个体和整体利益。 由仿真结果可以看出,在演化条件相同时,演化博弈最终可以收敛到唯一且稳定的均衡点,并且随着车辆规模的增大演化速度会降低,学习率也是可以影响演化速度的重要因素。与简单的车辆分簇算法相比,通过演化博弈算法将车辆分配给不同的参数服务器可以使收益最高、利益最大化。未来会进一步研究车联网下多种群的合作和竞争机制,并在其中考虑车辆的移动性因素,切实解决车联网下的移动性难题。3 仿真分析
3.1 实验场景及参数设置
3.2 演化博弈稳定性能分析
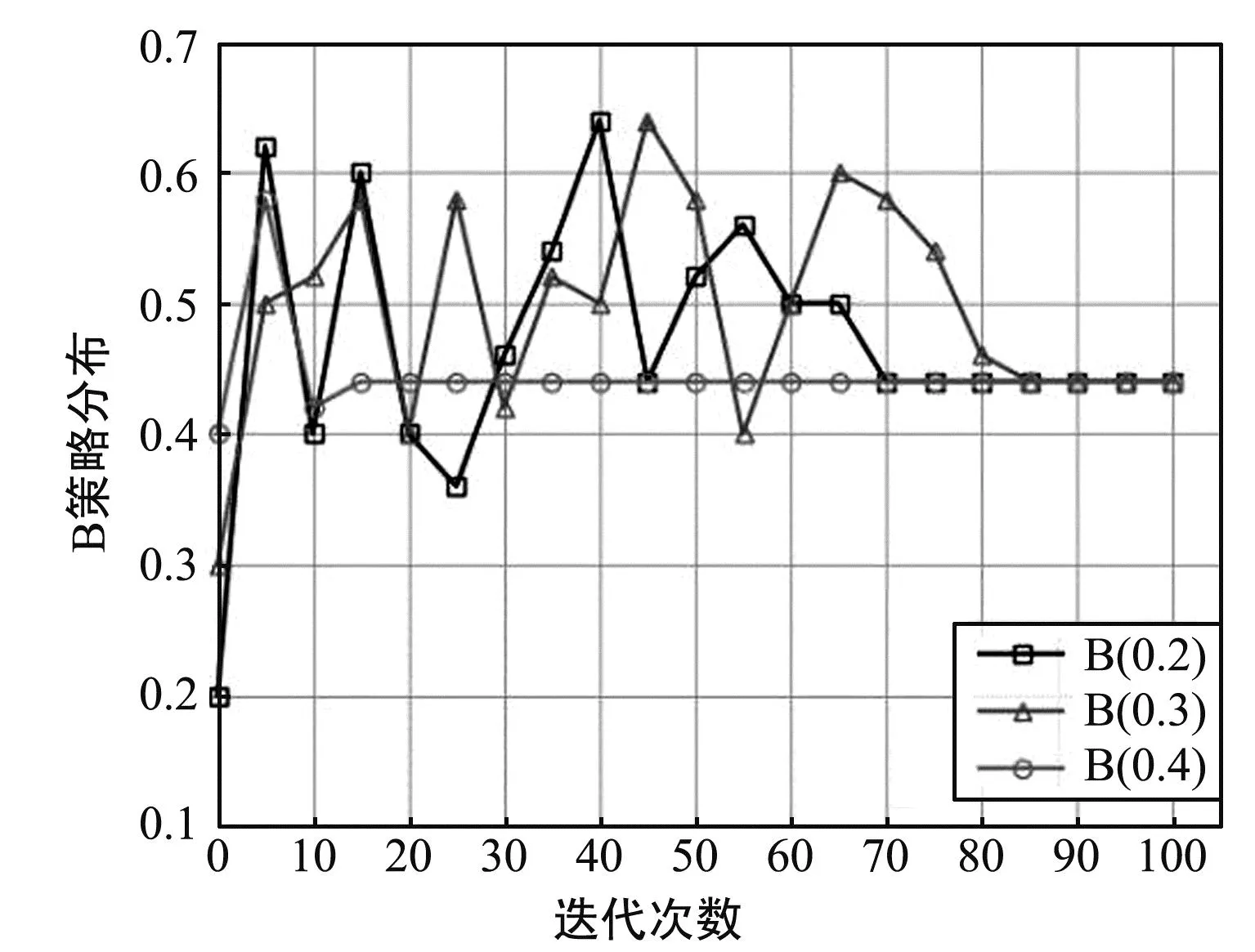
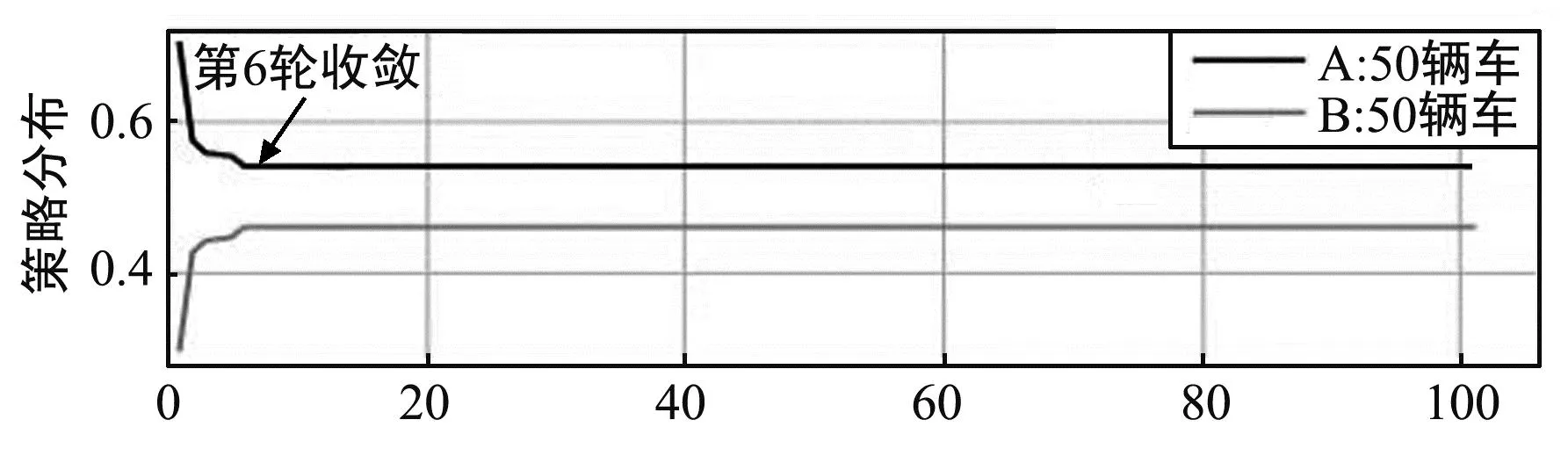


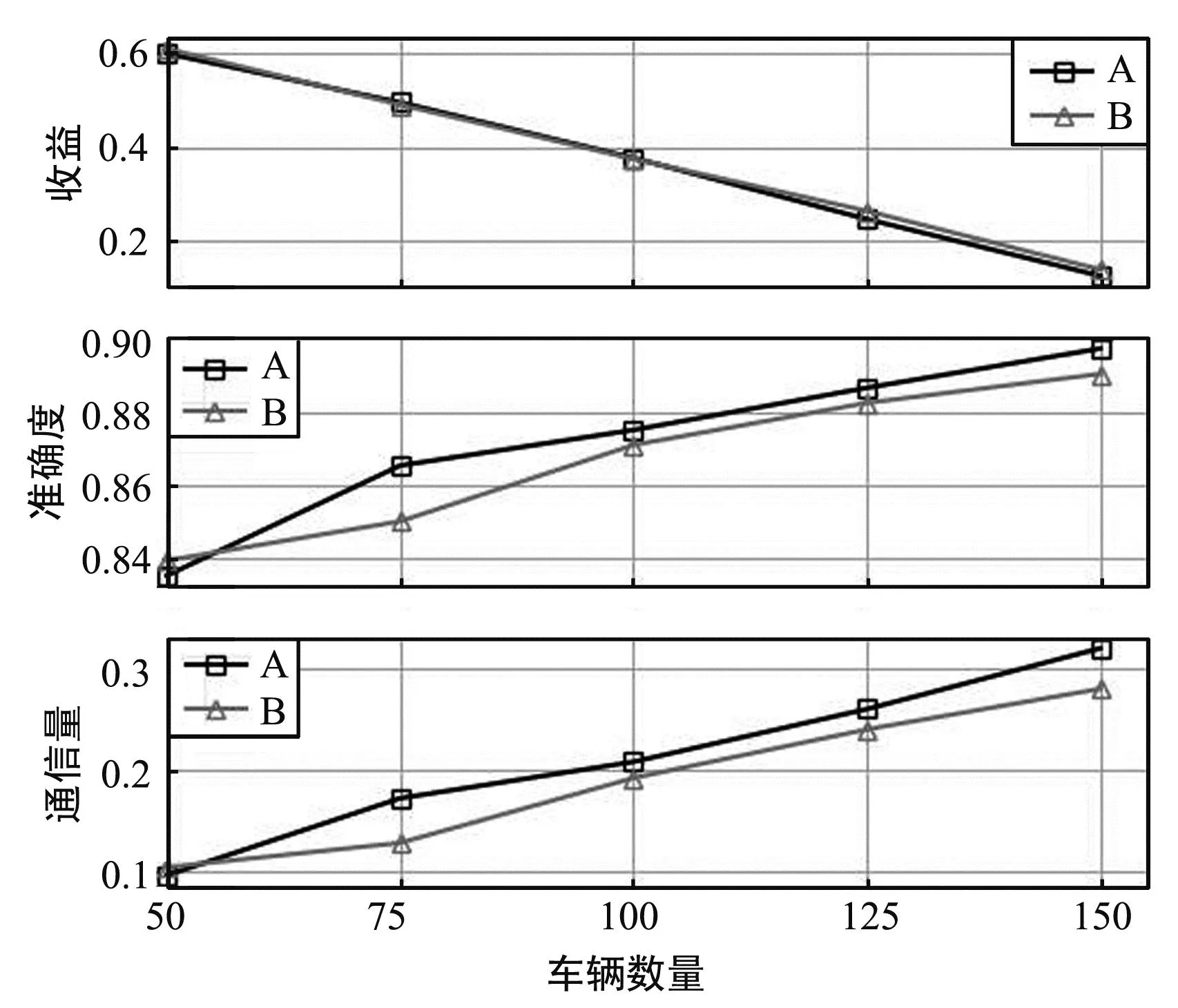
3.3 对比算法性能分析

4 结束语

