基于深度强化学习的多目标跟踪技术研究
杨麒霖,刘 俊,管 坚,莫倩倩,陈华杰,谷 雨,石义芳
(杭州电子科技大学 通信信息传输与融合技术国防重点学科实验室,浙江 杭州 310018)
0 引言
多目标跟踪问题是指由于目标的出现和消失,目标的数量及其轨迹随时间变化,根据传感器接收的量测数据联合估计目标数量及其轨迹的问题[1]。其本质是将量测和目标进行对应匹配,也就是数据关联问题。当杂波密集并且同时跟踪多个密集目标时,数据关联尤为困难。目前,广泛采用的多目标跟踪算法包括概率数据关联(Probability Data Association,PDA)、联合概率数据关联[2-3](Joint Probability Data Association,JPDA)滤波器、多假设跟踪[4](Multiple Hypothesis Tracking,MHT)和随机有限集[5](Random Finite Set,RFS)等算法。传统的多目标跟踪算法如JPDA和MHT侧重于数据关联,但在目标关联困难时很难有效解决问题,并且会消耗大量计算资源。
因此,基于RFS理论的滤波器应运而生。 Mahler[6]采用有限集统计理论提出了多目标贝叶斯滤波器的一种易于计算的近似方法——概率假设密度滤波器。它通过传递多目标后验密度实现多目标状态的估计。RFS不再过多关注数据关联,而是直接寻求多目标状态的最优和次优估计。RFS理论通过把多目标状态表示为一个RFS,从而使多目标能够在单目标贝叶斯估计相同的框架下进行处理[7]。在这一框架下,基于RFS的跟踪算法能够处理非常复杂的多目标跟踪问题。
但是,在RFS理论中多目标的状态是无法区分的,因此无法输出不同目标各自的航迹信息。为了解决这一问题,Vo等人[8]提出了标签RFS的概念,并提出了一种广义标签多伯努利(Generalized Labeled Multi-Bernoull,GLMB),它可以为每个目标的状态添加唯一的标签。由于GLMB分布是标准多目标似然函数的共轭先验,因而极大地方便了贝叶斯多目标滤波公式的计算,最终在GLMB分布的基础上,Vo等人[9]推导出能够输出目标航迹的 δ-GLMB滤波器。针对GLMB滤波器计算复杂度高的问题,Reuter等人[10]提出一种与之性能相近的近似实现方法——标签多伯努利(Labeled Multi-Bernoull,LMB)滤波器。之后,Vo等人[11]和Reuter等人[12]提出了一种将预测和更新结合为一的GLMB和LMB滤波器的有效实现方法,对于每次迭代只需要一个截断过程,便可以使用标准的分配算法来执行。
传统的多目标跟踪中采用的分配算法主要有Murty算法和Gibbs采样等。Murty算法的最优时间复杂度为O(KN3),最差时间复杂度为O(KN4),其中K为最优分配方案的数量,N为代价矩阵规模。而Gibbs采样虽然在运行耗时上有较大提升,但是会损失跟踪精度。特别是在大规模代价矩阵的最优化问题中,算法时间复杂度呈指数上升,将耗费大量的计算资源。
最优分配问题是经典的组合优化(Combinatorial Optimization,CO)问题之一,在CO领域中节约计算成本一直是研究者们致力解决的问题。通常来说,CO问题找到一个最优解需要消耗大量的时间成本。许多用于解决CO问题的传统算法是由领域专家设计的使用手工构建的启发式算法,这些启发式算法顺序地构造该类问题的解决方案,但是由于问题的复杂性,它通常不是最优的,并可能会耗费大量计算时间。近年来,随着机器学习领域的发展,人们发现将强化学习和其他技术应用于CO是可行而又有效的,因此,CO领域开始倾向于采用强化学习来解决问题[13-15]。
针对上述算法中存在的计算量大、运行时间长等问题,本文采用LMB滤波算法,结合利用CO领域中的深度强化学习技术,建立如图1所示的多目标跟踪算法模型。在尽量保证跟踪性能的情况下降低多目标跟踪算法计算负担,提升跟踪速度,以增强跟踪系统的实效性。
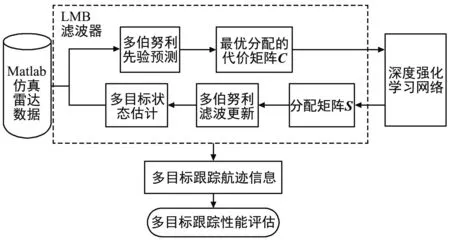
图1 系统结构模型Fig.1 System model diagram
1 LMB滤波器
1.1 标签随机有限集建模

(1)

鉴于RFS理论不能为多目标估计提供航迹信息,在标签RFS中引入了标签空间L的概念。

p0:k(X0:k|Z0:k)∝gk(Zk|Xk)fk|k-1(Xk|Xk-1)·
p0:k-1(X0:k-1|Z0:k-1)。
(2)
结合贝叶斯滤波框架,在标签RFS理论中,多目标状态预测和更新公式分别为:
1.2 滤波预测与更新
在标签RFS的基础上,Vo等人[8]提出了GLMB滤波,该滤波是一种满足共轭先验的贝叶斯滤波,即从当前时刻开始,如果多目标滤波预测密度满足GLMB的形式,则下一时刻的多目标密度也是GLMB形式。而LMB分布是GLMB分布的一种特殊近似。因此,LMB滤波器可通过贝叶斯预测和更新方程随时间向前递归传递LMB滤波密度。则LMB多目标预测密度为:
πk|k-1(X|Zk-1)=Δ(X)·
(5)

(6)

(7)
式中:i≤R表示存活目标i和量测j之间的关联概率,R+1≤i≤P表示新生目标和量测之间的关联概率,量测下标j的取值为[-1,M],其中j=0表示目标漏检概率,j=-1表示目标消亡或者未出生的概率。
由于目标状态和量测之间存在非常多的可能性,计算所有的状态与量测的组合是极其困难的也是不现实的,并且大部分可能性都需要被截断。通常采用的方法是求解以下最优化问题:
(8)
式中:S为分配矩阵,C为代价矩阵。将C中每个元素定义为:
(9)
代价矩阵C=[C1C2C3]由三个块组成:目标的漏检矩阵C1、消亡矩阵C2以及目标与量测的关联矩阵C3。表示漏检的C1矩阵是P×P对角矩阵,其中元素Ci,j为目标i漏检的可能性权值,所有非对角元素设置为零,C2矩阵对角线元素表示第i个目标消失或未出生的权重,其余非对角元素也置零;C3为P×M关联矩阵,其中每个元素表示对应目标到量测的关联权重。
2 基于深度强化学习的二分图匹配
2.1 问题定义
将要进行最优化分配算法的代价矩阵C定义为一个二分图G=(U,V,E),其中,U为含有P个元素的目标X集合,V为含有(2P+M)个元素的目标不同状态的集合,E为连接两侧节点的带权边的集合。
带权二分图如图2所示,图中左右侧分别为 二分图的U和V节点集合,两侧节点以不同权值的边相连接,有边相连的节点被称为邻居。其中,节点in1和in2分别表示目标xn的漏检和消亡状态(例如n在图2中的取值为1和2),i3、i4分别表示两个量测目标,连接两侧节点的边的权值为代价矩阵C中的非零元素。至此,代价矩阵的最优化任务转化为二分图的最大权重匹配任务。
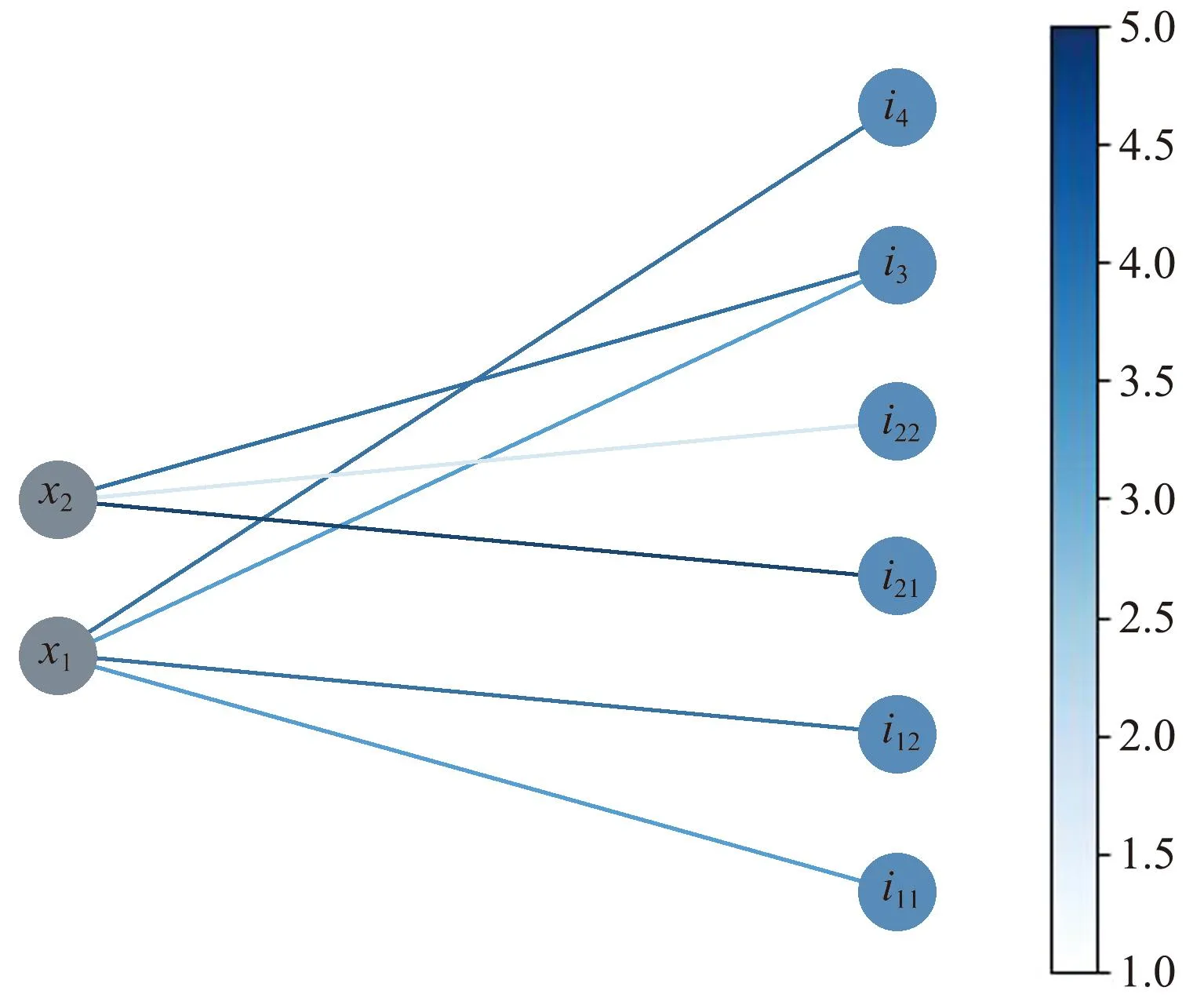
图2 带权二分图Fig.2 Weighted bipartite graph
2.2 强化学习与马尔可夫决策过程
强化学习是机器学习领域中的一种方法,强化学习讨论的问题如图3所示,图为在复杂不确定的环境中,智能体通过感知所处的状态s依据策略π采取不同的动作a与环境进行交互,从而获得最大的奖励r。
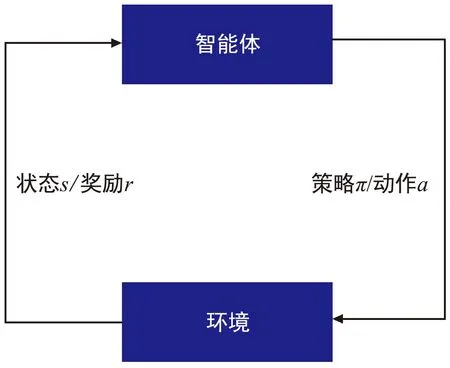
图3 强化学习Fig.3 Reinforcement learning
为了将强化学习应用于CO中,二分图匹配问题需要被建模为一个顺序决策过程,其中智能体通过执行一系列动作来与环境交互,以找到解决方案。马尔可夫决策过程为建模这类问题提供了广泛使用的数学框架。因此,将二分图匹配问题建模为一个马尔可夫决策过程。
状态空间S:空间S内的状态s是一组已选定的匹配和当前的部分二分图。当二分图的最后一个节点到达时s达到最终状态。
动作空间A:每个时间步长t时,节点vt及其边会一起到达。智能体可以选择将vt与其在U中的邻居进行匹配,也可以选择不匹配。因此,在时间t时,A中能采取的动作数量为|Ngbr(vt)|+1,其中Ngbr(vt)是节点vt的在U中的邻居节点集合。
奖励函数R:奖励r=R(s,a)定义为当前状态s下智能体采用动作a选择的边的权重。最终状态下的奖励r为二分图最终匹配方案的总权重。
状态转移:如果当前时间的节点vt被匹配给U中的节点,那么状态将会相应更新。无论当前节点是否匹配,都将进入下一状态并且下一节点与之前的动作无关。
2.3 深度学习架构
采用前馈神经网络作为强化学习的策略网络,当节点vt到达时,策略网络的输入5个特征向量的级联(w,m,ht,gt,nt)。特征向量w和m的级联为:(w0,…,wu,…,w|U|,m0,…,mu,…,m|U|)∈2(|U|+1),wu为当前节点vt与节点u的边的权重,mu表示该节点是否可以进行匹配的二进制标识。特征向量h,g,n包含一系列节点的历史特征。网络的输出是大小为|U|+1的概率向量。
2.4 算法训练
网络训练使用标准的REINFORCE算法[16]:
∇J(θ|s)=Epθ(π|s)·
[((G(π|s)-b(s))∇lnpθ(π|s)]。
(10)
为了减小梯度的方差,在训练迭代中添加了基线函数b(s),训练中基线函数b(s)初始化为匹配方案的奖励G(π|s)并以式(11)更新:
b′(s)=βb(s)+(1-β)G(π|s)。
(11)
2.5 模型输出
训练好的深度强化学习网络将输出代价矩阵的一个最优解S1。为了输出代价矩阵的k个次优解,在二分图G中将S1中的每个目标关联的边E(i,j)以及节点i和j的边删除,生成图G1;再将图G1作为模型的输入,输出次优解S2;以此类推即可输出k个次优解Si。
将多个次优解的集合矩阵S作为分配矩阵,向前传递多伯努利后验密度,完成一次完整的滤波更新。
3 实验结果与分析
为了验证本文算法的性能,设计了非线性条件下目标数较多的复杂场景下的仿真实验场景,包含了多目标轨迹交叉、平行等多目标运动状态。
设传感器位于坐标原点,传感器可获取目标和杂波共同生成的位置量测。传感器可检测区域为 [-2 000,2 000] m×[0,2 000] m的矩形区域,采样间隔为1 s。总观测时长100 s,在观测时间内一共有 15个真实目标出现,各目标运动轨迹如图4所示。

图4 目标真实轨迹Fig.4 Real tracks of targets
各目标初始状态及其起始、终止时间如表1所示,其中初始状态向量表示目标的x方向的坐标和速度、y方向的坐标和速度以及目标运动的角速度。杂波数量服从λ=10的泊松分布并在传感器监视区域内服从均匀分布。

表1 各目标运动状态
进行100次蒙特卡洛实验,对不同滤波器的跟踪过程的OSPA(2)误差[17-18]和运行时间进行统计。实验结果将本文算法记为LMB-DRL,基于两种不同分配算法的LMB滤波器记为LMB-Murty和LMB-Gibbs,除此之外还与GLMB滤波算法进行实验对比。各滤波器的运行时间和平均OSPA(2)如图5所示。
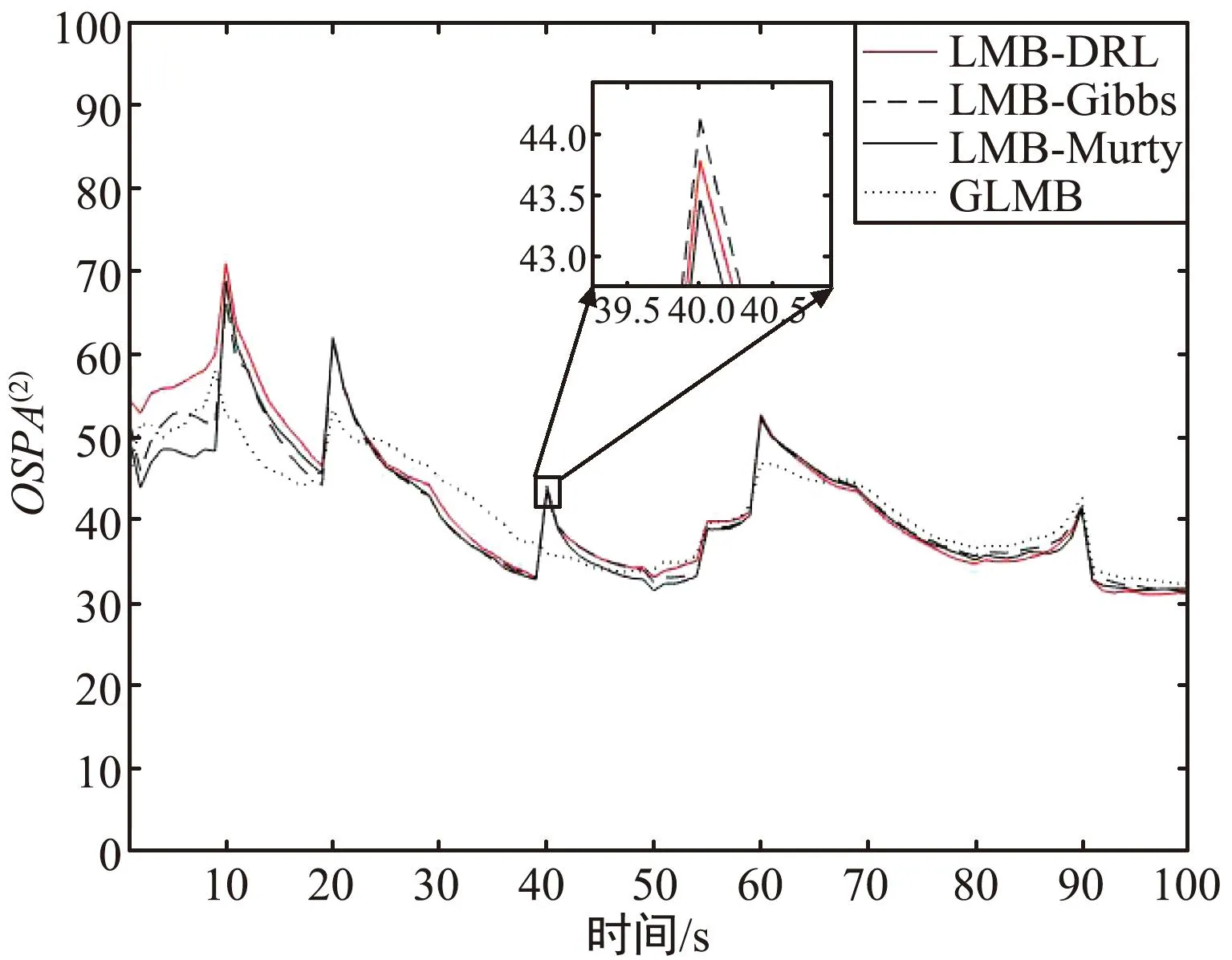
图5 平均OSPA(2)误差对比Fig.5 Comparison of average OSPA(2)
从图5和表2可以看出,LMB滤波器对新生目标不够敏感,在新目标出现时各LMB滤波器都会有较大误差,而GLMB滤波器在跟踪新生目标时的误差较小;LMB-Murty滤波器取得了最好的OSPA(2)性能,但是运行时间也是最长的;LMB-DRL在保证了跟踪性能的情况下,降低了运算成本,提升了跟踪的实时性,体现了本文算法的可行性。

表2 各滤波器运行时间和平均OSPA(2)对比
4 结论
提出了一种与深度强化学习结合的多目标跟踪滤波算法,在保证跟踪性能的前提下大大减少了跟踪过程的计算成本,特别是目标数量较多的跟踪场景中效果会更显著。但是由于滤波算法的分配环节的计算复杂度与深度强化的网络结构有关,因此即使是较为简单的场景也需要一定的计算复杂度。未来展望是设计一种自主学习的强化学习方法,在低复杂度的情况下使用启发式算法并训练学习匹配特征,高复杂度情况下自动决策进行最佳匹配。

