基于深度学习的室内目标波达方向估计

邓伟鑫,高 晖*,唐 勐,粟 欣,彭 莹,苏 昕

(1.北京邮电大学 信息与通信工程学院,北京 100876;2.清华大学 信息科学技术学院,北京 100084;3.中信科移动通信技术股份有限公司,北京 100083)

0 引言

随着无线通信系统的不断发展与演进,超五代及第六代移动通信将提供更高的技术指标[1]。当前,多输入多输出(Multiple-Input Multiple-Output,MIMO)系统具有高信号增益、强干扰抑制能力及高空间分辨力等优点[2-3],这使其有望同时具备通信和感知能力,实现高速率通信和高精度感知[4]。此外,随着移动互联网、物联网以及新型设备的快速发展,越来越多的智能化应用出现在人们面前,如室内定位及追踪[5]、人体活动检测[6]等,这些应用需要高精度、高实时的感知技术支持,快速准确的波达方向(Direction of Arrival,DoA)估计[7]是关键技术之一。与室外环境不同,室内环境下DoA估计面临多径和障碍的挑战,这些挑战导致接收信号幅相特性变化从而对DoA估计产生不利的影响,此外室内场景中行人身体姿态的变化及位置移动、大型机器设备的运动都将导致电磁特性复杂多变,传统DoA估计技术在室内场景直接运用时性能较差[8]。

传统的DoA估计方法,如最大似然估计(Maximum Likelihood,ML),通过求得方向估计似然函数的最优解来估计DoA[9-10];基于噪声子空间的多重信号分类(Multiple Signal Classification,MUSIC)方法[11],通过特征值分解划分信号子空间,然后根据噪声/信号子空间正交性估计DoA[12-13]。这些方法因高分辨率而得到广泛使用,然而多径环境将导致视距(Line of Sight,LoS)径信号分辨困难以及多径分量之间具有相干性,对传统方法估计精度造成不利影响,此外这些方法涉及多次迭代以及特征值分解等高复杂度运算,难以实现高实时性估计。因此亟待一些面向室内场景的高精度、高实时DoA估计技术。

1 相关工作

近年来,机器学习在解决信号处理问题方面显示出许多优势[14-15],一些研究将机器学习应用于DoA估计问题[16-19]。在传统的机器学习方法中,Malajner等人[18]提出了基于接收信号强度指示(Received Signal Strength Indicator,RSSI)和支持向量机的DoA估计方法,以RSSI为数据集使用支持向量机方法。董川源[19]提出了基于梯度提升树与集成学习原理的极限梯度提升(Extreme Gradient Boosting,XGBoost)方法来进行DoA估计。但这些方法仅对非多径环境DoA估计有效,受到多径环境的不利影响,难以解决过拟合、维度灾难等机器学习难题[20]。

相比传统的机器学习方法,深度学习(Deep Learning,DL)不依赖可解释模型设计,自主从大量原始数据中学习,提取数据高级特征。DL模型具备更好的预测性能,且训练好的网络只需要简单的推断就可以完成估计。现有基于DL的DoA估计研究一般以接收信号及其各种处理形式作为网络输入,以矫正的接收信号或预测角度等作为输出[21-26]。一些团队提出基于深度神经网络(Deep Neural Network,DNN)的DoA估计方法[23-24],通过训练多层隐藏层对目标DoA在角度域网格上进行分类。Chen等人[25]通过划分扇区分区域进行DoA估计,设计探测网络以及估计网络,前者对信源目标进行区域分类,后者进行DoA估计,降低了时间开销。此外,DL也可用于增强传统方法,Elbir[26]提出DeepMUSIC方法,设计了特征提取能力更强的卷积神经网络(Convolutional Neural Network,CNN)重构MUSIC谱峰函数以增强MUSIC方法,减少计算量并提高估计精度。这些研究针对特定场景构建数据集,取得了较好性能,然而在室内环境下仍具有局限：一是未考虑场景中未知多径信号的影响,严重扭曲信号的相位特性分布,降低了估计精度;二是面对多径环境没有刻意训练模型分辨LoS径信号的能力;三是尚未有研究考虑电磁环境变化的潜在挑战,模型不具备适应环境变化的鲁棒性。

对DoA估计方法展开研究,提出了一种基于DL的室内目标DoA估计方法,训练CNN用于室内目标DoA估计,并设计了一种基于小样本学习(Few-Shot Learning,FSL)的快速模型更新机制。将所提方法简记为FSL-CNN方法,进一步从DoA估计拓展到对目标位置的感知。主要研究内容如下：

① 提出了基于DL的室内目标DoA估计方法。设计了一个用于DoA估计的深度卷积网络,利用有监督的DL训练CNN对抗多径影响,提升模型从多径分量中分辨提取LoS径信号DoA特征的能力,并针对室内环境构建数据集,并以此为训练模型,训练完成的模型实现了高精度、高实时的DoA估计。相比ML、MUSIC等传统方法,所提FSL-CNN方法在时间复杂度上有显著优势;相比DNN、DeepMUSIC等DL方法,所提方法具有更高的精度和较低的时间开销。

② 基于FSL设计了在线学习机制。考虑提升模型在面对电磁环境变化情况下的鲁棒性能,预训练模型在首次部署时根据实际部署环境,在线学习少量数据,更新网络部分参数,完成模型微调。面对电磁环境变化的情况,基站按需获取新数据,快速更新模型。引入FSL[27-28]可以提高模型对环境的泛化性和鲁棒性,相比重新训练,所提在线学习机制具有更高效能。

③ 基于DeepMIMO数据集展开了仿真实验。在DeepMIMO的Indoor1[29]环境下进行仿真实验,结果验证了所提FSL-CNN方法实现的效能优势。作为应用示例,进一步讨论了基于DoA估计的多站协同室内目标定位方案,在室内环境下达到了0.017 4 m的平均定位误差。

2 系统模型

基于阵列天线构建了DoA估计方法所需的接收信号模型。如图1所示,考虑一个室内上行场景,以单基站为例,其为K名目标用户提供服务。基站具有M根接收天线,配备了均匀线性阵列,各阵元间距为d,取半波长,每名用户均配备单天线发射机。为了实现对目标用户DoA的估计,设定场景中来自K名用户的入射信号si(t)=[s1,s2,…,sNs]∈1×Ns,i=1,2,…,K;Ns是快拍数,来自不同用户的入射信号相互独立,且与噪声也相互独立。假设天线阵部署位置与目标用户具有足够距离,可将目标发射信号视为远场平面波。设定分别来自K名目标用户的入射信号方向角为θ1、θ2、…、θk。

图1 室内目标DoA估计场景Fig.1 Indoor target DoA estimation scenes

假设基站侧的接收信号表示为X(t)=[x(t),x2(t),…,xM(t)]T∈M×Ns,具体表达式为：

X(t)=AS(t)+N(t),

(1)

式中：A=[a(θ1),a(θ2),…,a(θk)]∈M×K是由K个阵列导向矢量组成的矩阵,导向矢量表示为M×1,i=1,2,…,K;S(t)=[s1(t),s2(t),…,sK(t)]T∈K×Ns表示来自K个不同信源的入射信号矩阵,N(t)=[n1(t),n2(t),…,nM(t)]T∈M×Ns表示噪声矩阵,其中各噪声向量满足独立同分布,并且有ni(t)～N(0,σ2),i=1,2,…,M;σ2为噪声功率。

进一步,如果环境中存在多径信号,设多径数为L(不包含直射径),则接收信号可改写为多径信号的求和。

(2)

为获取DoA信息,计算接收信号的协方差矩阵是一个良好的选择。以无多径为例,为不失一般性,忽略时间标签t,则接收信号的协方差矩阵RX∈M×M表示为：

RX=E[XXH]=ARsAH+σ2IM,

(3)

式中：Rs∈K×K为入射信号的自相关矩阵,由于信源信号与噪声之间不相关,可以得到AE[SNH]和E[NSH]AH为0,因而接收信号的协方差矩阵如 式(3)右侧所示。实际情况下无法根据式(3)求得概率平均值,因此如式(4)所示计算算术平均值来近似表示接收信号的协方差矩阵。由对称性,仅取协方差矩阵的上三角部分作为参数以减少输入神经网络的数据量：

(4)

3 基于DL的DoA估计

对基于DL的DoA估计框架、室内环境数据集构建、模型的设计训练以及更新4个重要组成部分进行详细介绍。

3.1 基于DL的DoA估计框架

估计框架包含离线训练、在线估计以及模型更新阶段,如图2所示。离线训练阶段通过大量数据训练模型;在线估计阶段输入采集的接收信号样本进行DoA估计;模型更新阶段基站按需通过当前采集数据对模型进行更新。估计模型以接收信号协方差矩阵上三角部分作为源数据输入,进一步执行数据预处理得到数据集：① 为方便DL模型处理,需要将复矩阵分成实部和虚部两部分,再通过扁平化重组成一维向量;② 为使样本向量在进行点乘运算或其他计算时拥有统一的标准,进行归一化处理。采用监督学习的方式训练模型,除对接收信号进行上述处理得到的数据集外,还需要输入与之对应的LoS径DoA角作为标签数据。

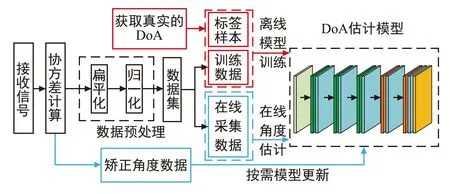
图2 基于DL的DoA估计框架Fig.2 DL-based DoA estimation framework

3.2 数据集构建

针对室内环境DoA估计构建数据集。DeepMIMO数据集[29]由Wireless Insite软件生成,是一个面向MIMO系统的公开DL数据集,其基于精确的3D射线跟踪方法生成,广泛支持基于DL的通信和感知应用。

依据DeepMIMO构建室内环境下DoA估计的数据集,选择实验场景为室内环境Indoor1。通过DeepMIMO数据生成器,依照场景中关键参数设置生成DeepMIMO数据集;其中包含大量信息,需要对所需信息进行提取,例如接收信号,基站与目标用户的位置、角度关系等。进一步,将该数据中的基站-用户角度信息作为标签数据y,然后对接收信号数据按算 法1处理得到室内目标DoA估计数据集。以预测的DoA结果作为网络的输出Z,构建网络的输入-输出对{d,Z}其中d∈M(M+1)×1、Z∈K×1分别表示网络的输入和输出,最终数据集构建方法如下。

算法1 数据集构建输入：数据集样本总数U,接收信号X,Z输出：数据集1：初始化u=1以及数据集长度U2：for 1≤u≤U do3：生成接收信号样本X(u)4：利用式(4)计算X的协方差矩阵R(u)X 5：双通道扁平化处理得到^d(u) = [Re(R(u)X ),Im(R(u)X )]T6：对^d(u)进行归一化处理得到d(u) =[cov(u)real,cov(u)Imag]T7：设计数据集输入(u)in={d(u)} ,输出(u)out={Z(u)} 8：构建数据集(u)={(u)in,(u)out}9：u←u+110：end for u

3.3 模型设计和训练

构建数据集之后,设计了DoA估计模型。该模型主要由卷积层和全连接层构成,具体如图3所示。将数据集馈送到神经网络中进行训练,采用多层神经网络模型对训练集进行求解,得到各神经网络节点的权值,根据最小化损失函数确定网络节点的最优权值。

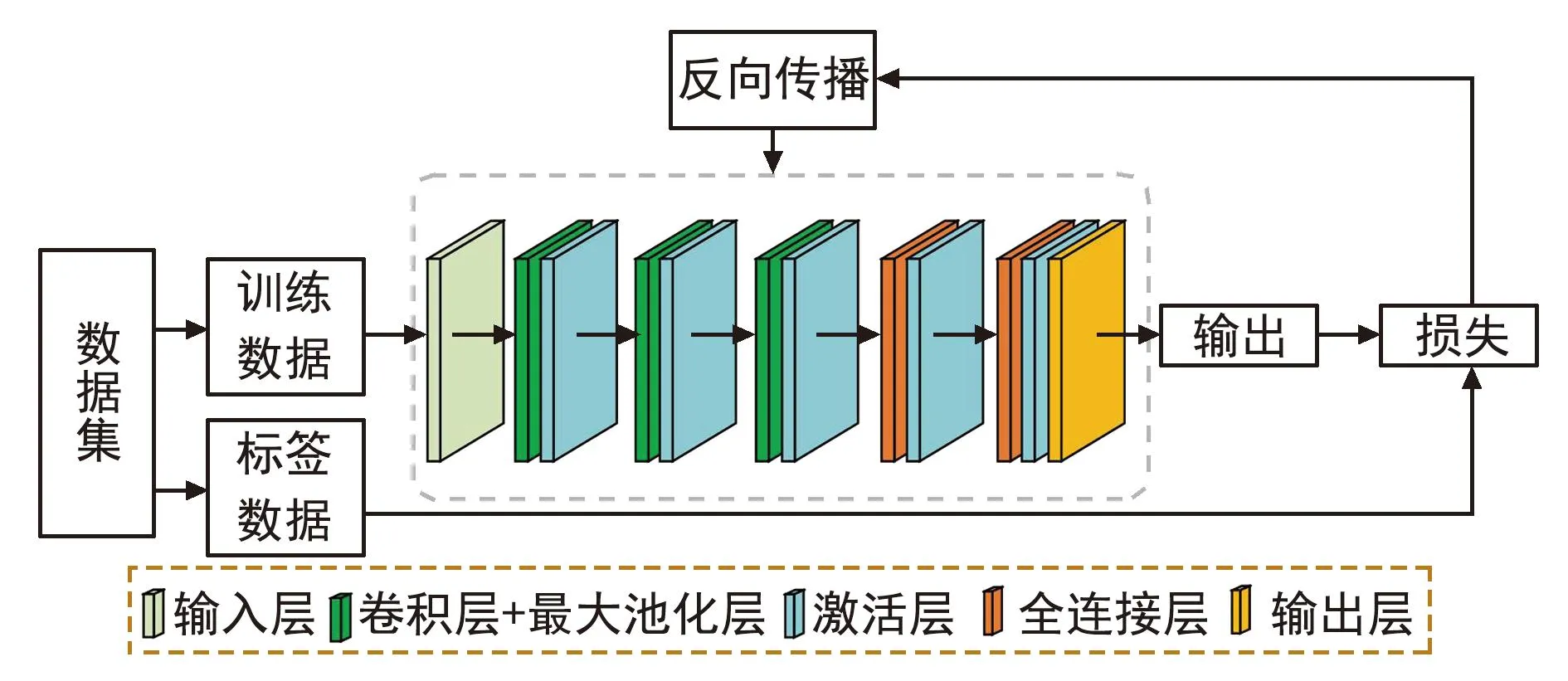
图3 基于DL的DoA估计之神经网络结构Fig.3 Neural network structure of DoA estimation based on DL

本文采用了卷积层、池化层、整流线性单元(Rectified Linear Unit,ReLU)激活函数层、全连接层等结构来设计深度卷积网络模型。网络模型的输入为：

d=[covreal,covImag]T,

(5)

y=[θlabel(1),θlabel(2),…,θlabel(k)]。

(6)

(7)

式中：f1(·)表示输入层,将输入数据传递给隐藏层;{fi(·)}i={2,5,8}表示卷积层,通过卷积运算提取数据中含有的DoA特征,尤其从多径分量中学习LoS径信号的特征;{fi(·)}i={3,6,9}、 {fi(·)}i={4,7,10,12,14}分别表示最大池化层、激活层,实现特征降维和非线性输出以提高模型学习能力;{fi(·)}i={11,13}表示全连接层,实现由特征到目标DoA的映射关系;f15(·)表示输出层。使用ReLU作为激活函数提升模型的学习能力,其表示为ReLU(x)=max(0,x)。

为不失一般性,每次训练假设使用相同的随机初始权重和偏置值。此外,为提高模型估计的准确性,使用Adam优化器[30]实现反向传播(Back Propagation,BP)方法,对模型参数进行调整。损失函数设计为当轮训练输出的DoA估计值和真实值的均方误差(Mean Square Error,MSE)：

(8)

3.4 DoA估计和模型更新

训练完成后各层网络权重固定,输入新采集的接收信号数据可实现DoA估计。为了使模型有效适应所部署的场景,使用了一种小样本增量[27-28]学习的策略,能够有机结合完成训练的模型和在线采集的数据,提升模型在实际部署中的准确性。具体的方法执行流程示意如图4所示,基站交替执行DoA估计和其他任务的同时,对新的无线数据进行采集,模型基于新的数据按需进行更新。

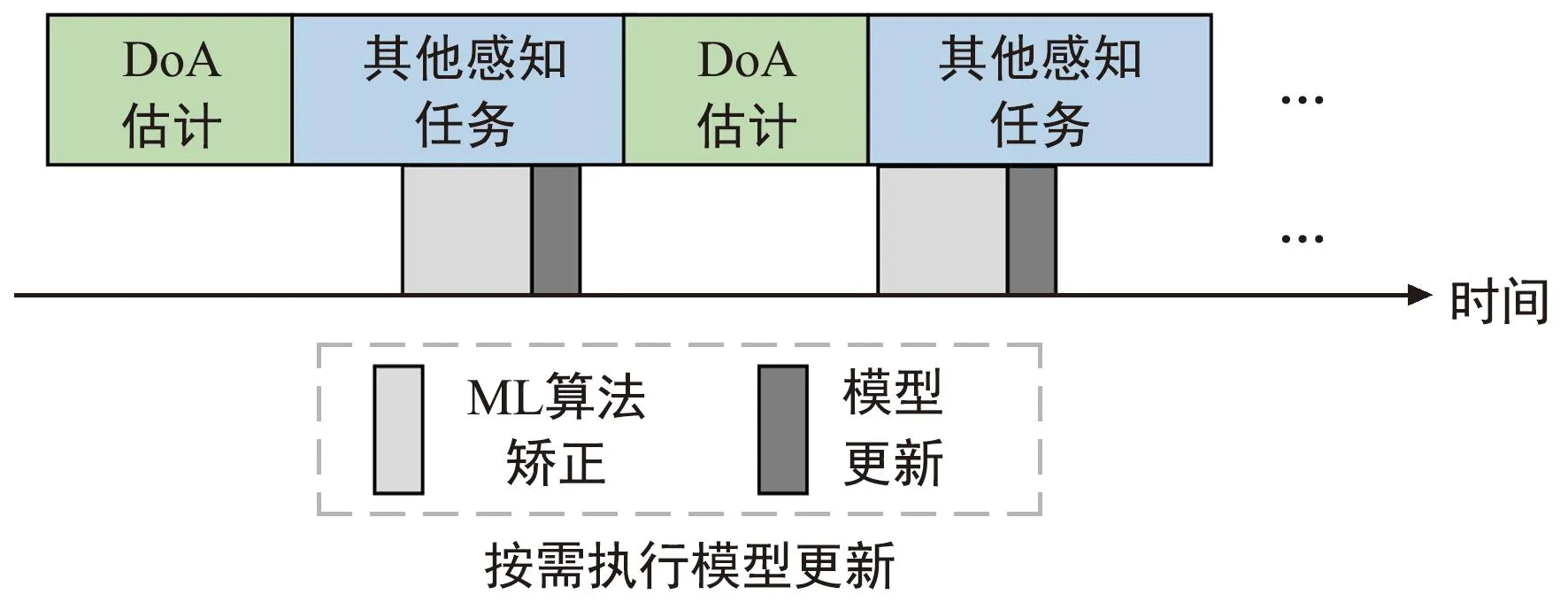
图4 方法执行流程示意图Fig.4 Schematic diagram of algorithm execution process

DoA估计阶段,基站采集当前场景下的阵列接收信号,并计算得到协方差矩阵。为保证数据的一致性,这一阶段使用与离线阶段相同的数据预处理操作得到在线估计阶段的数据,随后将在线估计阶段阵列捕获的数据输入到模型中进行估计。

执行其他感知任务阶段,基站基于已采集信号数据按需进行模型更新。需要更新模型时,基站根据所部署平台的计算资源情况,在不影响DoA估计及其他感知任务运行的前提下对少量接收信号数据执行ML方法得到校准的DoA,随后利用这些接收信号数据及其校准的DoA制作数据集作为模型更新阶段的输入。由于校准的DoA获取并行于持续运行的DoA估计及其他感知,因而进行所提方法DoA估计时间评估时忽略ML方法校准带来的高复杂度影响。

模型更新阶段,基于FSL思想更新模型。通过少量的训练数据来训练模型[27],以学习和识别新的实例。采用基于模型微调的FSL方法,通过增加新的训练样本,在已有描述旧数据的特征之上加入新数据的特征,不断更新模型的参数,使得模型能够适应新的类别[28]。这种学习方式可以使模型基于原有知识提高学习新知识的效率,而不会使新知识覆盖旧知识。基于上述思想,设计更新方案：模型在已有训练的基础上,仅依靠少量样本学习新的特征,基于式(8)和BP方法快速完成参数的更新,提高模型对不同环境的适应性。相比重新训练,在原有模型上进行更新,可以减少训练轮次,降低训练时间。

模型更新如图5所示,通过馈入少量新数据,更新全连接层的权重参数实现在线估计阶段模型快速更新。首先,根据实际部署的环境,当采集到新的少量数据时,对新数据进行预处理得到新数据集;然后,加载预训练模型,冻结参数使得在BP过程中这些层的权重固定不变,因为该部分结构具备了在多径环境下提取DoA特征的能力而无需在某个特定场景下再针对这部分结构进行调整;最后,设置优化器对全连接层进行训练,优化器的配置和离线阶段训练整个模型时的配置保持一致。调整全连接层是因为这一部分结构主要用于特征向估计角的映射,在不同环境下存在不同映射关系,针对特定环境进行特定映射关系学习将有效提高估计精度[22]。在已有模型基础上,这部分的更新仅需输入少量数据就能达到良好的估计性能。

图5 模型更新Fig.5 Model updating

3.5 时间复杂度分析

表1展示了各方法时间复杂度：ML方法首先需要计算协方差矩阵RX,然后基于交替投影方法搜索最优解,ML方法复杂度为O(Kp(M3+M2K+2K2M+K3)),p为最优解搜索次数;MUSIC方法计算协方差矩阵RX后进行特征值分解,最后谱峰搜索,因此MUSIC方法复杂度为O(s(M3+M2K+K2M)),s为谱峰搜索步数;本文所提方法计算复杂度取决于神经网络计算复杂度,具体为O(aM2+bK),其中a和b是与网络模型设置相关的常数。显然,引入DL可以实现更低的时间开销。

表1 时间复杂度对比Tab.1 Calculation complexity comparison

4 仿真结果与分析

4.1 仿真配置

本文仿真使用MIMO通信中具有代表性的DeepMIMO数据集[29]验证所提方法的可行性。设计场景为Indoor1生成的矩形房间,该室内场景中放置4个基站,分别部署在房间的4个角落,仿真DoA估计时设置某个基站开启工作。基站具有16阵元,场景信源数为2个,载波信号频率为2.5 GHz,信噪比(Signal to Noise Ratio,SNR)设为[-10∶5∶10] dB,多径数L为3(信号能量主要集中在L个多径分量上),快拍数Ns为512,谱峰搜索的间隔步长为0.1°。选择80 600个样本按8∶2比例划分训练集和测试集。网络训练具体超参数设置如表2所示。

表2 超参数表Tab.2 Hyperparameter table

衡量DoA估计性能的指标为均方根误差(Root Mean Square Error,RMSE),表示为：

(9)

本部分仿真选择如下DoA估计方法展开对比：所有方法在与所提方法相同的场景设置下对相同信源目标进行DoA估计。

① ML[10]：传统方法,通过ML方法以及交替投影法来估计DoA。

② MUSIC[11]：传统方法,利用子空间正交性进行DoA估计,并使用空间平滑方法实现解相干。

③ XGBoost[19]：基于梯度提升树与集成学习原理求解分类问题对DoA进行估计。

④ DNN[23]：DL方法,设计DNN输入接收信号协方差矩阵输出角度结果,对双目标信源进行DoA估计。

⑤ DeepMUSIC-CNN[26]：DL方法,设计CNN输入接收信号协方差矩阵输出MUSIC谱函数,通过CNN构建谱函数以强化传统MUSIC方法。

⑥ FSL-CNN：本文所提DL方法,输入信号协方差矩阵预训练CNN。模型部署具体环境后基于FSL更新CNN并输出目标LoS径角度估计结果。

4.2 DoA估计性能分析

图6和图7为在相同的室内环境下不同估计方法在精度和估计时间方面的比较。估计时间比较的方式是在一次DoA估计阶段内,以所提FSL-CNN方法估计时间为基准,比较其他方法估计时间与基准方法估计时间的倍数。从图6可知,FSL-CNN方法可以达到0.1°级别及以下的估计精度。相较于传统的机器学习方法XGBoost,所提方法采用DL,可以达到更高的估计精度;相较DeepMUSIC-CNN和基于DNN的DoA估计,所提方法具有性能优势,因为FSL-CNN考虑设计有监督的CNN提升模型对抗未知多径信号的能力,同时提高了分辨LoS信号的成功率。图7表明,FSL-CNN方法实现了估计时间的大幅减少,仅稍慢于DNN方法。因为DNN不涉及卷积结构,计算速度相对较快;除此以外所提方法均优于其他对比方法,比如估计时间仅为ML与MUSIC方法的万分之一,对比XGBoost、DeepMUSIC-CNN方法也是具有更低的时间开销。由此可知,所提方法针对DoA估计具有良好的实时性。

图6 不同方法性能对比图Fig.6 Performance comparison chart of different methods

图7 不同方法估计时间对比图(以FSL-CNN 为基准)Fig.7 Estimation time comparison chart of different methods (based on FSL-CNN)

图8为非多径模型分别在多径场景下从零开始重新训练以及基于所提FSL机制在线学习多径场景特征的归一化MSE收敛曲线对比图。在非多径环境下训练所提DoA估计模型,并使用该模型分别针对某一多径环境进行在线学习、重新训练。可以看出,所提方法可使模型快速适应所部署的多径场景。仅需要少量的训练轮次(50 epoch)便可基本修正模型的估计结果,收敛速度远快于从零开始直接训练(500 epoch)。

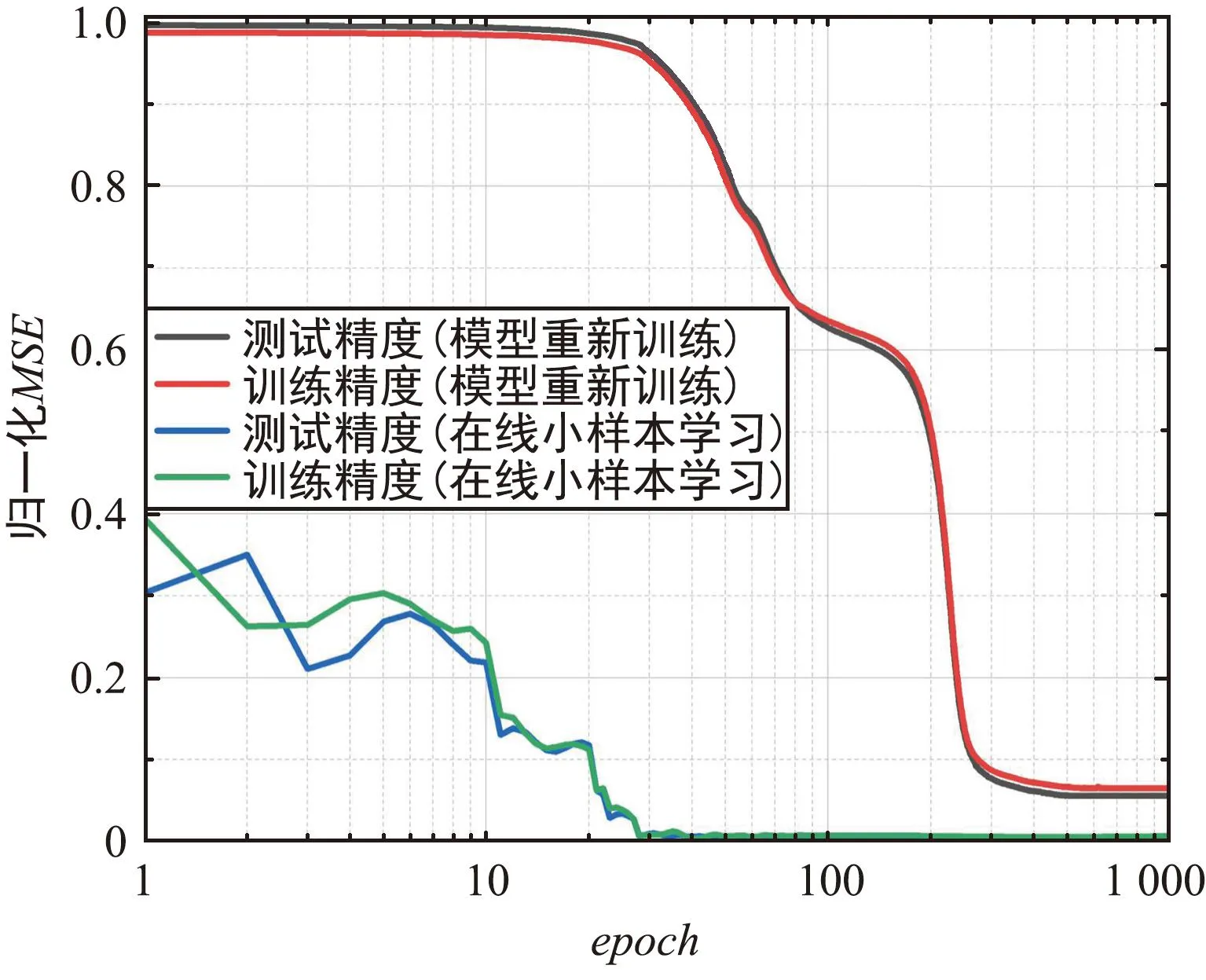
图8 在线学习与从零开始直接学习曲线对比图Fig.8 Comparison of online learning and learn from scratch

为验证在线学习机制具有提高模型快速环境适应能力的作用,在非多径环境下训练了所提的DoA估计模型。如图9所示,当模型不经过任何额外训练而直接应用到一个具有多径的室内环境时,显然其无法实现准确的DoA估计。因此,为使原始模型适应新环境,基于本文所提FSL机制对模型进行在线学习和更新(CNN with FSL),同时以重新训练的模型(CNN with Retraining)作为对比。模型经过在线学习后,可以快速适应新场景,能达到至少 0.1°的分辨率,性能表现基本与重新训练相差无几。

图9 所提方法在迁移到不同场景下性能对比图Fig.9 Performance comparison chart of proposed methods in migrating to different scenes

4.3 应用案例——多站联合定位性能分析

仅通过估计的DoA信息可以推广到对目标定位：由几何关系可知,如果场景中存在至少两个不共线的基站时可以确定一个位置坐标,因而联合两个基站的DoA信息可以实现对室内目标的定位。具体而言,由于基站位置先验已知,同时合理假设两个基站分享各自的DoA估计信息,则如式(10)所示计算可得目标位置坐标。

(10)

式中：(x,y)、(xR1,yR1)、(xR2,yR2)分别表示目标位置、基站1、基站2的坐标,{θR1,θR2}分别表示目标相对基站1和2的角度,σ表示可能存在的角度测量误差。

由于场景中存在许多障碍或目标距离基站较远的情况,部分基站估计DoA精度不高,将导致定位不准,而部署多站可以有效增加覆盖并提高定位精度。针对部署多站的场景,在两站几何式定位基础上提出一种基于接收信号强度的最优基站选择机制,依据接收信号强度选择最优的两个基站,并基于所选基站估计的DoA信息如式(10)所示计算目标位置,完整的方法流程如算法2所示。

算法2 多站联合目标定位方法输入：n个基站的接收信号Xki(t),i=1,2,…,n,k=1,2,…,K输出：目标位置估计(xk,yk),k=1,2,…,K1：for 1≤k≤K do2：对于第k个目标,根据接收信号强度Pr=Xk(t)22选择强度最高的两个基站Sa、Sb,位置分别记为(xa,ya)、(xb,yb)3：对所选基站Sa、Sb执行DoA估计方法,获得估计角度θka、θkb4：利用式(10)计算目标位置(xk,yk)5：k←k+16：end for k

假设场景中4个不共线的基站开启工作,为用户提供定位服务。在这一场景下选取2 000组测试数据分别进行仿真,每组数据仅包含一个目标,2 000组数据的单目标均匀分布于水平面高度为1 m的场景中。对比两种多站联合定位方法：① 任选两个基站执行估计方法,得到两个基站的DoA数据,再进行几何定位;② 采用所提多站联合目标定位方法选择连接质量最好的两个基站,再进行几何定位。结果如 图10所示,x轴与y轴共同表示目标在x-y平面上的位置,z轴为该目标的定位误差值,误差值以欧氏距离表示。计算平均定位误差可得：方法①为0.020 2 m,方法②为0.017 4 m。由于方法①随机两站定位方法可能使用了信号质量较差的基站数据,因而导致较高平均定位误差;而方法②选取了质量更佳的两站执行几何定位方法,将平均定位误差降低至0.017 4 m。

(a) 随机两站定位

(b) 选取最佳两站定位

5 结束语

对基于DL的室内目标DoA估计进行研究,提出了一种高效且环境适变的方法,解决了现有方法效能不佳的问题。所提FSL-CNN方法根据实际部署情况,在线学习快速更新模型,适应复杂的室内场景,有效提高估计的性能,进一步基于估计的DoA信息提出了一种多站联合定位方法。仿真结果表明,所提方法能达到0.1°及以下的估计精度,相对于大多机器学习方法以及传统估计方法,可以实现更短的估计时间。在不同室内环境下,模型通过在线FSL快速适应新环境,仿真表明经在线学习后的模型估计DoA能够达到0.1°级别的分辨率。在推广到多站联合定位时,可以达到0.017 4 m的平均定位误差,实现高精度定位。所提方法为室内DoA估计提供了一种方案,未来将对通感一体化场景下的高实时性、高鲁棒性感知展开深入研究。