基于SEM的土体微观结构三维分析与分维计算方法

张豫川,高旭龙,刘东发,黄鸿伟

(1.兰州大学 土木工程与力学学院,兰州 730000; 2.兰州大学 西部灾害与环境力学教育部重点实验室,兰州 730000)

0 引 言

土体在长期的历史沉积过程中,形成了多孔的微观结构形态。微观结构直接决定土体宏观工程力学性质[1],也决定着土体外部环境改变时新结构的变化趋势[2]。土体微观结构研究一般包括颗粒形态与分布[3]、颗粒之间的接触与排列、孔隙的形态与分布、孔隙间的孔喉连接[4]与迂曲程度[5-6]等内容。土体微观结构的研究,对认识渗流[7]、变形、物质运移与水土保持等宏观现象规律,揭示土体强度的维持与丧失等物理力学特性机理有极其重要的意义。

扫描电子显微镜(Scanning Electron Microscope,SEM)能无损、有效地获取微观信息,已广泛应用于土体微观结构的分析中[1,8-9]。一般将SEM图像二值化,用黑白两色分隔孔隙与颗粒后进行量化研究[10-11],但是阈值的选取对分析结果有直接影响,得到的视孔隙率、颗粒或者孔隙的平面面积与周长等参数不具备直接分析的意义[11],将原本灰度值丰富的SEM图像转为只有0与255两个灰度值的黑白图也舍弃了大量可供处理与分析的信息。为了避免阈值选取,尽可能保留SEM图像信息,王宝军等[12]利用图像处理技术结合地理信息处理系统(Geographic Information System,GIS),从黏性土微观SEM中得到了三维视孔隙率等结构参数;徐日庆等[13]通过分析软土SEM图像,建立三维空间计算模型,开展了SEM分析对软土孔隙率计算的影响研究;Li等[14]利用GIS技术分析固化污泥的SEM图像,研究了固化污泥在生物降解过程中的微观结构变化。

复杂的土体微观结构难以用传统欧式几何准确量化,而分形理论在描述土体等结构复杂且具有自相似特征的多孔介质结构方面有着独特优势。分形理论由Mandelbort[15]提出后,最早由Tyler和Wheatcraft[3]引入土体学的研究中,分形维数可以定量表征土体结构,已在土体理化性质描述[16]、渗透、空间变异统计[17-18]等诸多方面有了成功的应用。土壤学研究中很早便建立了三维空间的分形维数模型及其分形维数的计算方法[3],但所需的计算参数很难由常规土工试验数据得出,导致其在土体研究中的应用受阻。Tyler等[3]和杨培岭等[19]假设同一土体颗粒具有相同密度,从土体颗粒质量分布计算分形维数,这一假设与实际情况不符[20],应用效果也差强人意[21]。土体孔隙分布的分形维数与颗粒不同,准确测量需要使用分子吸附法[22]。

本文对陕西定边与甘肃兰州的原状土样进行SEM试验,基于SEM图像三维化处理技术以及三维曲面表面积、体积计算方法,计算了土体视孔隙率、比面等结构参数,提出了三维化处理后微观结构分形维数计算的实现方法。本文提出的方法可以仅由SEM图像得出土体颗粒与孔隙的分形维数,无需额外的测定试验,是土体微观结构SEM图像处理与分形维数计算的新路径。

1 SEM图像三维化处理方法

SEM图像是灰度图像,用纯白(灰度值为255)、纯黑(灰度值为0)以及二者之间一系列过渡色记录观测结果。扫描中发射出的电子束在样品观测面激发二次电子,被探测器收集,表现为或亮(白)或暗(黑)的差别,这个扫描成像过程与自然光照射在物体表面后反射类似,距离探测器较近的区域(凸起的颗粒)亮度较高,在图像中更趋近于白色,距离较远处(下凹的孔隙)更趋近于黑色。

二值化处理是预先选定灰度阈值,低于此阈值的像素点灰度值归为0,记录为孔隙范围,高于阈值者归为255,记录为颗粒范围,由此将灰度图像转为黑(孔隙)-白(颗粒)二值图。

SEM图像三维化处理无需使用阈值划分,保留了灰度信息,其原理是在平面图像x-y两个维度基础上,增添由灰度值转换而成表征观测面起伏的z维度坐标,形成三维图像。如图1所示,取3 pixel×3 pixel的平面像素空间为例,在图像平面内建立x-y坐标系以描述各像素点位置,将每个像素点的灰度值转为z坐标值,即

图1 二值化与三维化处理SEM图像原理对比Fig.1 Comparison between binary and three-dimensional SEM image processing principles

z(x,y)=g(x,y)。

(1)

式中:z(x,y)为三维化后(x,y)像素点的z坐标;g(x,y)为SEM图像中(x,y)像素点的灰度值(无量纲)。

2 分形维数计算理论基础及实现原理

2.1 分形维数计算理论基础

分形维数是基于分形理论研究土体微观结构的重要参数,具有明确的统计意义,土体的微观结构可以用孔隙、颗粒等方面的分形描述。下面给出三维化处理后土体微观分形模型的定义与计算方法。

欧式维数为E(E∈[1,3] )的几何体如果是分形体,那么它的量度可用式(2)表示[23],即

G(ε)=G0εE-D。

(2)

式中:ε为尺度;G为ε尺度下的量度;G0为分形系数(常数);D为分形维数。

式(2)适用于分形曲线、面积与体积的量度。当E=1,G与ε对应于长度,此时D∈[1,2);当E=2,G与ε对应于面积,D∈[2,3);当E=3,G与ε对应于体积,D∈[3,4)。以E=1为例,分形维数D在几何上描述了曲线的不规则程度,D越小,曲线越光滑,一维欧氏空间中的任意光滑(规则)曲线的分形维数D=1;D越大,曲线越曲折,越不规则,D→2的极限情况下,曲线极不规则,趋近于填充整个二维空间。

对于E=2的情况,分形体的量度G变成了面积S,此时分形维数DS表征了表面积的不规则程度,即“表面起伏分形维数”

S(ε)=S0ε2-DS。

(3)

两边取对数即可得到分形维数DS的计算式为

(4)

可改写为

(5)

式中S0为对应于表面积S的分形系数。

假设土体微观颗粒(孔隙)表面具有分形性质,SEM图像三维化处理后,利用三角形不规则网格原理求取表面积S(ε),计算尺度ε取SEM图像最小像素尺寸的整数倍,则相邻像素点水平间距j=ε,j或者ε取值越大,表面积S(ε)计算精度越低,反之精度越高,可得到不同ε对应的S(ε)计算值。由式(5),作S(ε)/ε2-ε双对数图,若可线性拟合,则证实土体微观颗粒(孔隙)表面积具有分形性质,分形维数DS即为拟合直线的负斜率。

上述DS的定义与用正方形格子覆盖海岸线计算分形维数的方法[23-24]类似,故也被称为“盒维数法”或“覆盖法”,得到的分形维数DS也被称为土体结构的表面起伏分形维数。

2.2 分形维数计算的实现原理

2.2.1 土体孔隙与颗粒的识别

三维化处理后灰度的明暗转为z方向坐标值的高低,形成了试样观测面的直接映像,此三维化的起伏表面即是颗粒与孔隙的分界面。如图2所示,在三维化图像的最低点作一与x-y面平行的平面,此最低面与分界面之间的空间认定为颗粒,类似地,最高面与分界面之间的空间认定为孔隙。

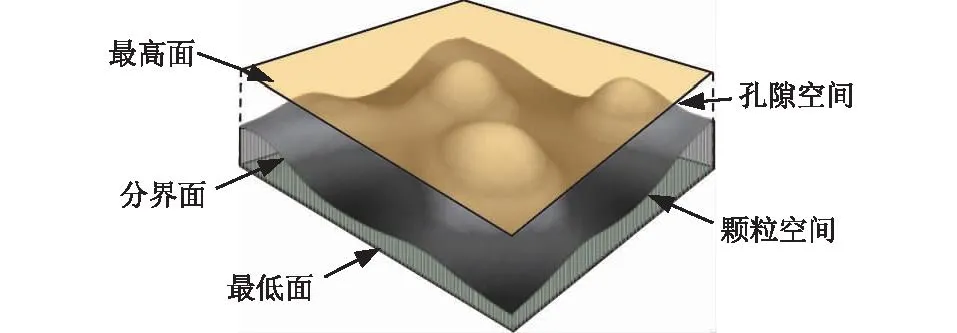
图2 土体孔隙与颗粒的识别示意Fig.2 Identification of soil pores and particles

2.2.2 颗粒(孔隙)的表面积与体积计算

孔隙与颗粒的表面积、体积等几何参数是计算分形维数的基础,可利用三角形不规则网格原理[25-26]计算。如图3所示,三维化起伏面上取4点A、B、C和D,将坐标点相互连接可得到两个空间三角形,它们的面积之和可作为这4点所围区域的表面积近似值,4点所围区域与任意平面之间的空间体积,可用空间三角形与该平面所夹体积近似,缩小4点之间的间距,即可逐渐逼近精确值。

图3 三角形不规则网格计算原理示意Fig.3 Calculation principle of triangular irregular mesh

用海伦公式计算图3中空间三角形面积之和,即

(6)

其中:

式中:Si为第i个不规则网格空间面积之和;|AB|代表图3中A、B两点距离,以此类推。各点之间距离用空间坐标计算。

令Δx=xi+j-xi,Δy=yi+j-yi,假设SEM图像由m×m个像素点构成,则三维起伏面的表面积S可由式(7)得到

(7)

将图3所示2个五面体沿顶面的最低点分割为三棱柱与三棱锥后计算空间三角形与x-y平面所夹空间体积,即

(xi+j-xi)(yi+j-yi) 。

(8)

由m×m个像素点构成的SEM图像,三维起伏面与x-y平面所夹空间体积V为

(9)

分形维数DS定义的一个特点是分形维数由测量尺度ε与计算值S(ε)、V(ε)之间的关系得到。SEM图像经过三维化处理后,联合三角形不规则网格原理计算不同精度的S(ε)、V(ε)计算值,可以实现DS的计算。

3 三维化处理与分形维数计算实例

3.1 试验材料与仪器

试验用原状土样分别取自陕西省榆林市定边县与甘肃省兰州市城关区青白石。定边土样编号为DB,兰州土样编号为LZ。基本土力学指标与颗粒的粒度分布如表1所示。

表1 试验用土样基本土力学指标与粒度分布Table 1 Basic mechanical indexes and particle size distribution of soil samples for the test

已有的试验研究结果[7]表明,两地土体都为湿陷性黄土,但渗透、应力响应等宏观性质有较大差异,这正是二者微观结构不同的体现。故而选择定边与兰州两地土样进行微观结构观测,对比二者的微观结构量化参数,并在此过程中说明本文提出的三维分析与计算分形维数等结构参数的方法。

原状样自然风干,避免迅速失水引起的土体结构变化[27],之后切削成直径7 mm左右的柱体,使试样可以放置在基座上。在柱体试样中间用小刀轻划一圈划痕,沿划痕掰断试样,得到保持结构原始状态的新鲜断面。喷金处理后移入JSM-6510型扫描电子显微镜,观察试样微观结构特征。

3.2 SEM图像三维化处理

DB、LZ这2个样品放大到500倍(10 pixel/μm)SEM图像如图4所示。图像尺寸均为2 560 pixel×1 920 pixel。

图4 样品的SEM图像Fig.4 SEM images of samples

ArcGIS技术可将灰度值转换为数字高程模型(Digital Elevation Model,DEM)中的高程,即z维度坐标值,实现第1节所述SEM图像三维化处理。具体操作步骤与DEM的详细内容,可参见参考文献[28] ,三维化处理后的图像如图5所示,三维图像根据z坐标值映射了色彩,用白色小箭头标示观察方向。

图5 样品SEM图像三维化处理Fig.5 Three-dimensional processing of SEM images

3.3 分形维数计算结果

利用三角形不规则网格原理求取颗粒(孔隙)表面积S(ε)与体积V(ε),设定尺度ε=1,2,5,10,20,40,80,相应地改变计算网格大小可得到不同计算尺度下的S(ε)与V(ε)计算值。尺度为1时的计算值即为此SEM图像所能计算的最精确值,放大尺度,计算量减小,但精度降低。不同计算尺度的SEM图像示意如图6所示。

图6 部分计算尺度的SEM图像Fig.6 SEM images of samples in partial calculation scale

图7(a)是颗粒(孔隙)表面积计算值与量测尺度双对数关系曲线,表面积计算值随尺度不断增大而大幅降低,DB样在尺度取值范围内可线性拟合,LZ样在尺度取值1～20范围内线性拟合效果较好,尺度>20后拟合效果逐步变差。图7(b)是孔隙体积计算值与量测尺度关系曲线,体积计算值精度变化不如表面积计算值敏感,且存在一临界值,临界值内计算精度不会有明显降低,临界值与观测土体微结构本身、观测比例以及SEM图像的像素总数等因素有关,本次试验的临界值为20。

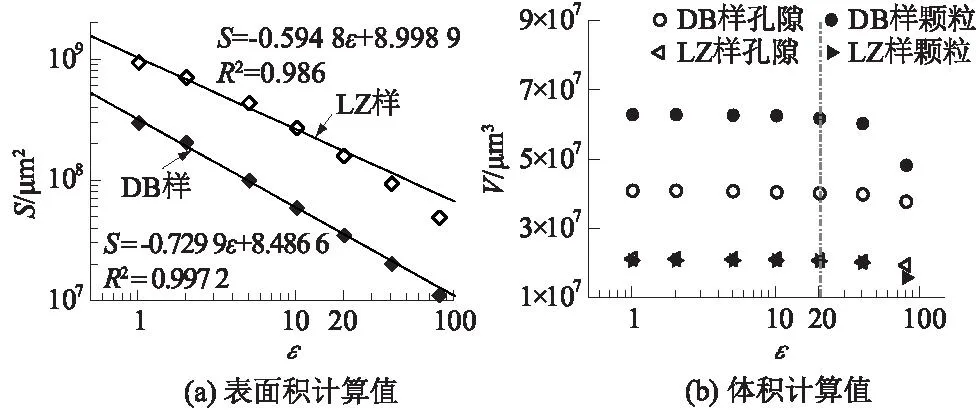
图7 计算值与量测尺度关系Fig.7 Relationship between calculated value and scale

土体孔隙的S(ε)/ε2-ε双对数图如图8所示。

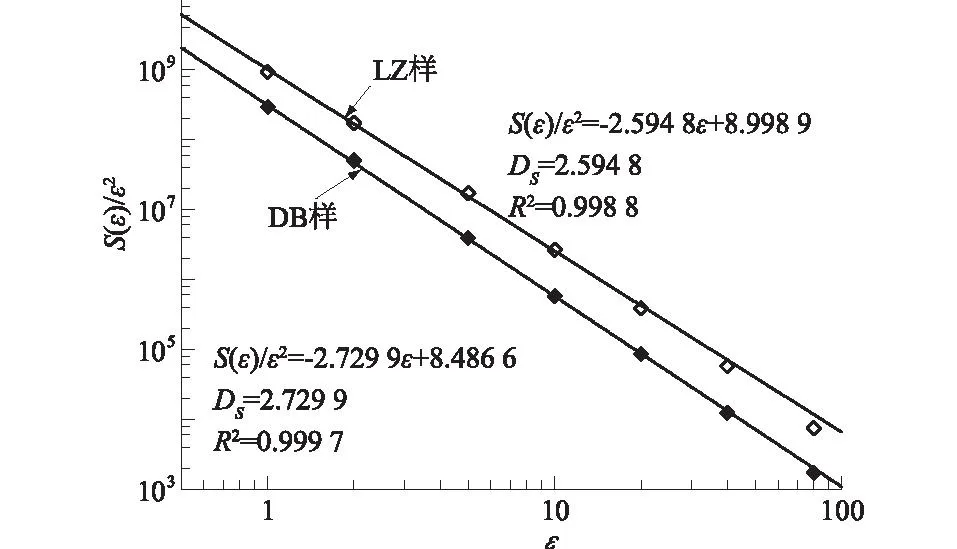
图8 分形维数计算的双对数图Fig.8 Double logarithmic curves for fractal dimension calculation

图8中DB样与LZ样均可线性拟合,且拟合效果较好,表明二者颗粒(孔隙)的表面起伏具有分形特征。分形维数计算结果汇总如表2所示。

表2 分形维数计算结果Table 2 Results of fractal dimension calculation

表面起伏分形维数DS描述孔隙表面起伏的不规则程度,DB样的DS为2.729 9,大于LZ样的值2.594 8,表明DB样的孔隙表面起伏不规则程度大于LZ样,DB样孔隙表面较LZ更加“粗糙”。

3.4 分形维数的验证与应用举例

土水特征曲线是非饱和土本构关系的重要组成,以分形维数在土水特征曲线预测中的应用为例,验证本文提出分形维数实现方法的计算结果。

用分形理论描述土体孔隙结构特性,可以得到非饱和土的土水特征曲线预测公式[21],即

(10)

式中:Se为有效饱和度, 由残余含水量θr与饱和含水量θs标准化得到, 若认为θr为0, 则有效饱和度Se与饱和度Sr相同;ψ为基质吸力;ψa为进气值, 指土体脱湿过程中气体开始涌入孔隙时的基质吸力值;D为孔隙表面分形维数, 用本文中的DS表征。

试验值由SOILMOISTURE公司生产的2100f小型张力计测得,分形模型预测结果与试验值比较如图9所示,其中进气值ψa由最小二乘法对试验点的最佳拟合得到。分形预测曲线与试验值较为一致,印证了本文提出的三维化分形维数计算实现方法的可靠性。

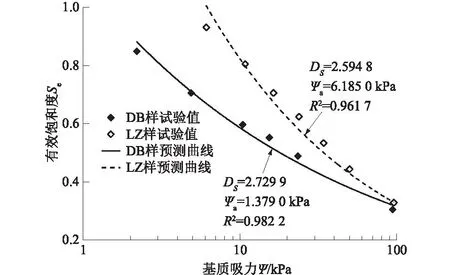
图9 分形模型预测结果与试验值比较Fig.9 Comparison between fractal model calculation results and experimental results

4 视孔隙率与比面的计算

SEM图像经三维化处理不仅可以得到分形维数,在实现土体结构表面的颗粒(孔隙)表面积S(ε)与体积V(ε)计算后,取ε=1时(最精确)的计算值还可以得到土体的视孔隙率与比面这2个观测面的重要微观结构参数。

4.1 视孔隙率与比面

孔隙率是土体最重要的微观结构参数,SEM图像只能得到观测面的微观结构信息,所得孔隙率可以称之为“视孔隙率”,计算式为

(13)

式中:n为试样观测面的视孔隙率;Vv为孔隙(三维化图像的最高面与分界面之间的空间)体积;Vs为颗粒(最低面与分界面之间)体积。

比面一般定义为土体固体(颗粒)骨架的总表面积与土体总体积之比,是土体等多孔介质传热、渗流、增脱湿等过程中十分重要的结构参数。三维化处理后可得到观测面的颗粒(孔隙)表面积以及颗粒与孔隙的体积,由此得到比面,即

(14)

式中:Ω为比面,量纲为长度的倒数L-1;S为颗粒(孔隙)的表面积。土体等多孔介质的比面可以理解为单位体积内的孔隙表面积,比面越大,颗粒分布越分散,结构越复杂。

4.2 视孔隙率与比面计算结果

SEM目前常见的二值化处理也可得到视孔隙率,其值为黑色与白色区域的面积之比。三维化、二值化以及由常规土工试验所得孔隙率对比见表3。

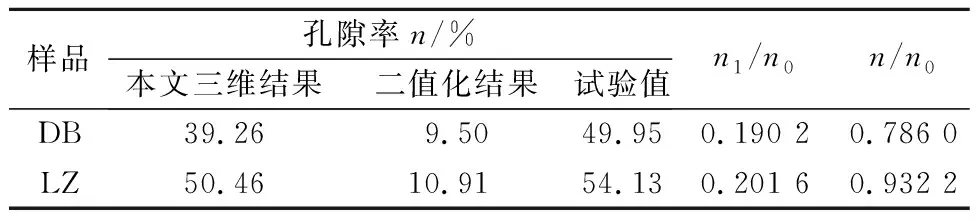
表3 孔隙率计算结果Table 3 Calculation results of apparent porosity

本文提出的三维化处理结果与试验孔隙率更为接近,这是因为二值化处理通过设定阈值分割颗粒与孔隙,计算模型精度较低;三维化处理无需此种操作,计算精度主要取决于原始SEM图像的像素点多少,以及设定的计算网格大小,因而相同观测比例,三维化视孔隙率与试验孔隙率更为接近。

需要说明的是,视孔隙率是观测面孔隙状态的反映,而试验孔隙率表征的是试验土样体单元的孔隙状态,二者概念不同,无法完全等同。从试验结果可知,本文的三维化结果较二值化更加接近试验孔隙率,表明三维化视孔隙率一定程度上能够表征真实孔隙状态,有望成为土体微观结构定量分析的工具之一。

三维化处理后的比面计算值如表4所示。DB样的比面Ω为2.809 6 μm-1,LZ样为22.318 1 μm-1,DB样Ω仅为LZ样的12.56%。LZ样比面大于DB样,表明LZ样的颗粒更小,颗粒分布更为分散,这一结论从二者的粒度分布试验结果中可以得到验证。

表4 比面计算结果Table 4 Calculation results of specific surface area

5 结 论

本文在已有的分形维数定义基础上,提出了针对土体微观SEM图像的三维化处理以及分形维数计算实现方法,通过定边与兰州两地原状土样的微观结构观测实例验证了该方法的有效性。主要得出以下结论:

(1)三维化处理无需选择阈值,保留了SEM图像的灰度信息,可以实现微观结构表面的三维重建和可视化,计算得到观测范围内土体颗粒(孔隙)的表面积与体积,继而获取视孔隙率、比面等土体微观结构参数。

(2)分形维数DS的计算均可由测量尺度与计算值之间关系得到,本文提出的三维化处理与三角形网格原理联合方法,可以计算土体颗粒(孔隙)不同测量尺度ε对应的S(ε)与V(ε)计算值,由此实现分形维数的计算。

(3)试验所用定边与兰州土样的微观颗粒(孔隙)表面均具有分形特征。定边土样表面起伏分形维数DS为2.729 9,兰州土样DS为2.594 8,定边土样的孔隙表面起伏不规则程度大于兰州土样。

(4)计算得到的分形维数在土水特征曲线预测方面应用效果良好,印证了本文提出的三维化分形维数计算实现方法的有效性与可靠性。