考虑韧性提升的输电网灾前预防检修多目标多阶段优化

梁海平,石皓岩,王铁强,鲁鹏,曹欣,杨晓东

(1.华北电力大学(保定),河北 保定 071003; 2.国网河北省电力有限公司,石家庄 050021)

0 引 言

近年来,极端气象灾害频发,其对电网造成的影响愈发严重,由此产生的经济损失不断增加[1]。2016年第14号台风“莫兰蒂”登陆我国福建,造成多条500 kV线路损坏。2019年第9号台风“利奇马”对浙江电网造成了巨大影响,华东及华北区域浙江、福建、上海、江苏等省共计停电38座110 kV及以上变电站、168条110 kV及以上线路,停电759.17万用户[2]。为了减轻极端灾害给电网带来的经济损失,国内外研究人员将“韧性”概念引入电网,以评价电网应对极端自然灾害的能力。

电网韧性,又称电网弹性或恢复力,通常指电网应对极端自然灾害、系统严重故障等小概率高风险事件的能力。目前,电网韧性评价指标仍处于探索之中,研究共识一般将其分为灾前预防抵抗能力、灾时响应吸收能力,以及灾后快速恢复能力[3-5]。其中,在系统灾前预防阶段,电网通过态势感知、灾害预测、预防检修、物理加固等措施提升系统抵御灾害能力[6-8]。

目前,针对电网灾前预防的韧性提升策略已有一定研究。文献[9]主要研究了台风灾害影响下输电系统的韧性指标的分析方法,并分析了提高元件承受最大风速这一措施对韧性提升的效果。文献[10]运用模糊隶属函数与模糊规则,提出一种在复杂电网系统中替代组件以及结构的措施来增强电网系统韧性。文献[11]从更换杆塔、植被管理的角度出发,构建了脆弱线路加固、确定停电设备、停电成本最小的三层优化模型,并运用贪婪算法求解。文献[12]针对电网提升应对台风灾害能力,提出了一种针对性的电网元件加固策略框架。根据以上研究可以看出,现有电网灾前韧性提升策略大多从预测灾害影响范围出发,对高风险元件进行替换或者改善,较少考虑设备自身的故障率。实际上,由于电网各个设备健康程度不同,健康程度欠佳、故障率高的设备更易在极端灾害下发生停运故障。

为了充分提升输电网韧性,文章提出以输电网灾前预防检修作为提升电网抵御极端气象灾害的措施。文章以基于蒙特卡洛模拟的场景分析法构建了考虑韧性的输电网灾前预防检修决策过程。以输电网灾时韧性、灾前检修风险、灾前检修经济性构成优化指标,构建输电网灾前预防检修多目标多阶段优化模型。通过IEEE RTS-79算例以及灾害场景模拟对所提的优化模型进行了仿真验证,仿真结果表明输电网灾前预防检修多目标多阶段优化模型的有效性,优化结果可帮助电网调度运行人员做出科学、合理地决策。

1 考虑提升韧性的输电网灾前预防检修决策过程

1.1 韧性评价指标

在输电网遭受极端灾害影响期间,电力设备可能发生大范围停运故障,系统可能采取削负荷甚至解列等紧急措施,系统供应的负荷水平下降。因此,通常将系统供应负荷水平作为输电网韧性的核心要素。在研究输电系统遭受极端灾害的韧性时,通常将系统状态分为：吸收状态、退化状态、降额运行状态以及恢复状态。

设灾害发生的时刻为T0,T0表示系统进入吸收状态,此时系统元件尚未出现损坏,系统仍维持正常水平。T1表示系统进入退化状态,该状态下输电系统元件由于灾害影响发生大范围破坏,系统维持负荷供电水平能力开始下降。T2为系统降额运行状态的起始时刻。T3为系统恢复状态的起始时刻,T4为灾后恢复状态的结束时刻,此时系统供电能力恢复到原有水平。设定灾前预防检修为T0时刻以前的一段时间内电网采取的措施。由于灾后恢复阶段的性能与所提出的方法关系不大,故考察T0至T1的吸收阶段,以及T1至T2的退化阶段电网韧性提升效果,如图1所示。

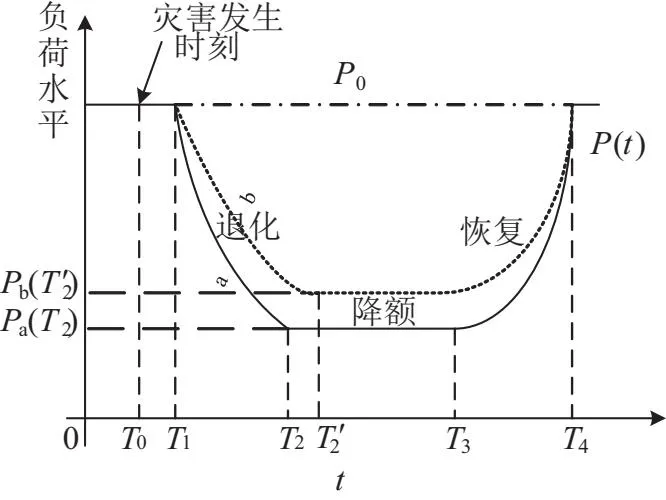
图1 输电系统遭受极端灾害的系统状态变化曲线

设正常状态下系统负荷水平为P0,退化阶段系统实际的负荷水平为P(t)。显然,图1中在T1至T2时刻内由P0、P(t)曲线所围成的面积为退化阶段内的输电系统缺电量(Energy Not Supply,ENS),有：

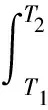
(1)

在图1中a、b表示两条不同的退化过程曲线,可以看出,适应阶段实际负荷水平P(t)的下降越缓,下降率越小,输电系统缺电量越小,其灾害适应力越强,输电网的灾后经济损失越小,输电网韧性越强。此外,系统在T0至T1的时间越长,则表明电网系统吸收力更强,阻滞负荷跌落能力越强。

根据以上思想,提出灾害风险抵御力(Disaster Risk Resistance,DRR)作为输电韧性评价指标,公式如下：

(2)

式中pij(t)表示第i个母线的第j个实际负荷水平;pij0表示第i个母线的第j个正常负荷水平;Nb表示节点数量;nLi表示第i个母线的负荷数量。可以看出,DRR既反映了系统的适应力,又反映了系统的吸收力。

1.2 基于场景分析的韧性评估

研究极端气象灾害对电网设备影响的方法可分为概率分析法与场景分析法[12],由于极端气象灾害属于小概率高风险事件,其对电网设备影响的历史数据量较少,概率分析法拟合的效果有待提高。场景分析法根据气象学与物理学等相关模型构建,能够克服历史数据不足的缺点,因此采用场景分析法对灾时电网韧性进行评估。

1.2.1 极端气象过境场景构建

文章以台风为例研究极端气象灾害对电网的影响。为了较为快速的计算出灾时气象因子,采用Holland风场模型[13-14]。该风场模型根据台风中心与台风边界的压强差来计算某一时刻的梯度风速值,忽略地转偏向力影响后,计算如式(3)所示：

VG=[AB(pn-pc)exp(-A/rB)/ρrB]1/2

(3)

式中pn为台风边界压强;pc为台风中心压强;r为距台风中心半径;ρ为大气压强;A、B为尺度参数。各参数取值参见文献[14]。将梯度风速乘以转换因子后即可得到近地表风速,通常转换因子取0.8[12]。

1.2.2 考虑气象因子与健康指数结合的设备故障率模型

文章主要研究输电线路因灾损坏,大部分文献仅将气象因子作为电网设备损坏的唯一因素[15],然而由于投运时间、外界环境等因素,输电线路自身健康状况也影响着设备的故障率。文献[16]提出了一种可以结合设备自身健康状态以及天气情况的输电设备故障概率模型,其表达式为：

P=(β/η)(Teq/η)β-1·exp(γ1Z1+γ2Z2+γ3)

(4)

式中η为比例系数;Teq为设备等效运行时间;Z1为设备健康状态类别;Z2为气象环境分级;β、γ1、γ2、γ3为历史数据拟合参数。

式(4)中天气环境根据三态模型获得了三种取值,但在灾害场景分析中,电网设备所处的气象条件随时间连续变化,将气象因素进行简单的分级没有细致地刻画灾害场景时设备故障率的变化情况。因此,对Z2进行改进,表达式为：

(5)

式中w为某时刻电网设备风速;wcrit为电网设备临界风速,当w>2wcrit时,令电网设备故障率P=1,即风速过大将造成设备直接损坏。

文章采用单元分割法[9]将各条输电线路划分为基本单位。设各单元故障率相互独立,线路整体故障率为：

(6)

式中PL为第L条线路故障率;mL为第L条线路单元数;PLi为第L条线路第i个单元故障率。

1.3 考虑提升韧性的输电网灾前预防检修框架

从改善输电网设备健康程度来抵御极端气象灾害的角度出发,考虑韧性指标,提出输电网灾前预防检修框架,如图2所示。极端灾害态势感知为根据气象数据或预警信号,对极端灾害提前感知,检修部门由常规状态进入灾前警备状态。

图2 输电网灾前预防检修框架

根据预测的气象数据,以及此时设备的健康状态,对灾前预防检修计划进行多阶段、多目标优化。灾前阶段,考虑电网检修风险与电网检修经济性两个目标。灾时阶段,考虑预想极端气象场景以及预防检修降低故障率的作用,对灾时电网韧性指标进行评估。检修部门根据优化结果应急开展灾前应急预防检修工作。

灾时电网韧性指标评估具体流程如图3所示。首先构建极端气象经本电网境内的气象因子时空预测场景,读取设备健康状态,从而构建灾时电网元件故障率模型。根据该模型进行时空蒙特卡洛模拟,生成灾害故障场景,随后计算灾时电网韧性指标。其中,灾害故障场景生成步骤如图3右侧框图所示。

图3 输电网灾时韧性评估流程

2 基于韧性提升的输电网预防检修多目标多阶段优化模型

2.1 电网灾前检修经济性评估

灾前电网检修阶段,首先确定待检修线路及其检修所需费用。设xi为二进制变量,取值为1表示第i条线路被选为待检修线路,反之为0。设检修线路总数量为Nl,则有决策变量X=(x1,x2,x3,…,xNl)。电网检修经济性表达式为：

(7)

式中bi表示第i条线路检修时长;c表示单位时间费用。

2.2 电网灾前检修风险评估

在考虑韧性提升的同时,应充分考虑在灾前应急检修阶段的电网运行风险。传统的检修风险通常采用蒙特卡洛模拟法或枚举法进行计算,但由于韧性评估已经采用蒙特卡洛方法计算,采用传统方法计算检修风险将使计算量陡增,求解效率低下。根据已有文献不难发现,检修计划风险性优化的主要目的是将检修计划的停电重叠程度降至最小,以避免随机停运故障导致的削负荷。为简化求解过程,从单一线路检修风险出发,提出检修重叠风险目标。

2.2.1 单一线路检修风险

综合考虑线路潮流熵脆弱度[17]、电压偏移、负荷损失因素,采用变异系数法[18]计算各指标权重,得出第i条单一线路检修时的风险,记为Rsi。Rsi的计算过程如下：

设支路断开潮流转移熵为V1,表达式为：

(8)

设节点扰动熵为V2,表达式为：

(9)

潮流熵的脆弱度指标Vi为：

Vi=V1iV2i

(10)

式中V1为支路断开潮流转移熵,表示支路i断开对系统造成的风险;V2为节点扰动熵,表示支路i抵抗节点功率扰动能力的大小,其余定义详见文献[17]。

设电压偏移量指标ΔUi,其表达式如式(11)所示：

(11)

式中UjN为母线j的额定电压值;Uij为检修任务i执行时,母线j的电压值。

对于检修线路i,选出除该线路以外5个故障率最高的线路作为故障事故集,进行N-1计算,通过最优潮流法计算负荷损失,并将其累加。其表达式如式(13)所示：

(12)

根据变异系数法,Rsi表达式为：

Rsi=(α1yi1+α2yi2+α3yi3)

(13)

式中αi为各项指标的权重;yik为第i项检修任务第k个经过同向化、归一化后的指标值。

2.2.2 检修重叠风险

定义检修重叠风险目标表达式如下所示：

(14)

式中Rsi表示第i条线路检修时的单一风险;y为二进制变量,表示第i条线路t时刻的状态,取值为1表示正在检修,反之取0;T为灾前检修计划总时长;Ntask表示待检修任务数。设第i项检修任务的开始时间为tstarti。检修风险评估满足以下约束：

(15)

yi,t=1,∀i∈Ntask,∀t∈[tstarti,tstarti+bi]

(16)

(17)

1≤tstarti≤T,∀i∈Ntask

(18)

1≤tstarti+bi≤T,∀i∈Ntask

(19)

以上约束中,式(15)表示上层决策变量选取的检修线路作为下层模型的优化范围。式(16)、式(17)表示检修不间断约束。式(18)、式(19)表示检修起始时间与检修结束时间均要求在规定的预防检修期间内。

2.3 电网灾时韧性评估

2.3.1 期望灾害风险抵御力

灾害发生时,电网设备故障为随机事件。基于1.1节提出的DRR,将其取期望作为灾前预防优化目标,表达式为：

(20)

式中ξ为随机场景;pi(ξ)为场景ξ的概率;Np为场景总数。

2.3.2 灾时最优削负荷模型

由式(2)、式(20)可知,电网韧性指标与电网供给的有功功率有关,此外在极端气象灾害下,输电网络可能会发生大规模故障,甚至系统解列,因此必须对发电机出力重新平衡,甚至负荷削减。考虑以上因素,同时不考虑灾害过程中电网的暂态情况,采用直流开断最优削负荷模型[19-20],目标与约束如下所示：

(21)

Bij(θi,t-θj,t)-PLij,t+(1-LSij,t)M≥0,∀i,j∈Sbus,t

(22)

Bij(θi,t-θj,t)-PLij,t-(1-LSij,t)M≤0,∀i,j∈Sbus,t

(23)

-LSij,tPLmaxij≤PLij,t≤LSij,tPLmaxij

(24)

(25)

(26)

0≤PCi,t≤PDi0,∀i∈Sbus,t

(27)

PGgmin≤PGg,t≤PGgmax,∀g∈i,i∈Sbus,t

(28)

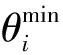
2.4 设备等效运行时间及健康状态回退

当设备完成检修后,对设备的等效运行时间及健康状态进行回退。此外,由于预防检修过程以及极端气象灾害时间较短,因此假设除检修活动导致回退效应以外,电网设备的等效运行时间及健康状态不发生变化。其表达式为：

Teqi=1,t∈[tstarti+bi,T2],∀i∈NT

(29)

Z1i=1,t∈[tstarti+bi,T2],∀i∈NT

(30)

Teqi=Teq0i,∀t,∀i∉NT

(31)

Z1=Z10i,∀t,∀i∉NT

(32)

3 NSGA-II算法与数学规划求解器结合的求解方法

文中建立的基于韧性提升的输电网预防检修多目标多阶段优化模型包含灾前检修经济性评估、灾时韧性评估、灾前检修风险评估三个主目标函数,且包含直流最优削负荷、检修风险重叠最小两个子问题。三个主目标函数彼此之间可构成帕累托前沿,其中子问题为线性化规划问题,可用数学求解器求得精确解,避免智能算法在计算变量较多、维数较高的而带来的“维数灾”问题。因此采用快速非支配排序遗传算法[21](Nondominated Sorting Genetic Algorithm II, NSGA-II)与Gurobi规划求解器相结合的方式进行求解计算。

NSGA-II算法是Kalyanmoy Deb等人提出的一种基于精英保留策略的多目标进化算法,其特点是采用精英保留的快速非支配排序,以减小算法时间复杂度。该算法主要有初始化种群、适应值计算、快速非支配排序、选择、交叉、变异、拥挤度计算等步骤。Gurobi是由Gurobi Optimization公司开发的数学规划求解器,其支持求解连续和混合整数线性问题;凸目标或约束连续和混合整数二次问题;含有绝对值、最大值、最小值、逻辑与或非目标或约束的非线性问题。

将二进制编码将决策变量X作为算法的个体构成种群。计算F1时可直接根据式(7)得出计算结果,计算F2时需将X作为该子问题(式(15)～式(19))的参数,调用Gurobi求解器,计算F3时参考图3灾时电网韧性评估流程以及式(29)～式(32),采用蒙特卡洛模拟法计算韧性指标,在计算最优削负荷时,为了加快求解速度,调用Gurobi求解器。算法流程如图4所示,图中虚线方框部分表示个体适应度计算,其展开过程如图4下方虚线方框所示,其中F2目标与F3中最优削负荷模型调用Gurobi进行求解,在三个目标适应度计算完成后,传递至NSGA-II算法进行非支配排序与精英保留策略等操作,直至迭代结束,得出Pareto前沿。

图4 NSGA-II与Gurobi联合求解流程图

4 算例分析

4.1 算例设计

本算例以IEEE RTS-79系统[22]为例,并假设其位于我国东南沿海地区。各线路地理位置分布以及单元分割情况参照文献[9],如图3所示,其中数字编号为节点编号,直线表示输电线路。

台风以2016年第4号强台风“妮妲”为例,其登陆过程路径如图5虚线所示。台风数据采用中国气象局热带气旋资料中心(tcdata.typhoon.org.cn)的卫星分析热带气旋尺度资料[22]。采用与文献[9]相同的气象数据处理方法,采用0.5 h仿真步长,对时间与台风中心位置采用线性插值,最大风速半径、最大风压闭合曲线半径取相邻两组数据最大值。其中,取2016-7-30 00：00 为台风的初始时间。

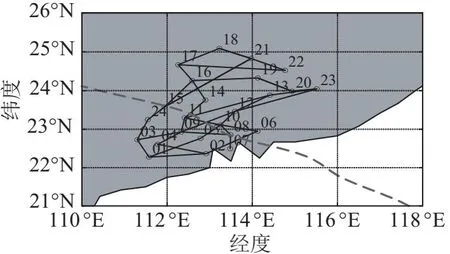
图5 输电系统地理位置

输电系统各线路的材料参数如表1所示,预防检修前各线路的Teq、Z1如表2所示。

表1 线路材料参数

表2 各线路Teq、Z1情况

灾前预防检修计划以天为最小单位,设计划总时长T=15(天),各线路单位时间费用c=10(万元/天)。各线路检修时长bi如表3所示。

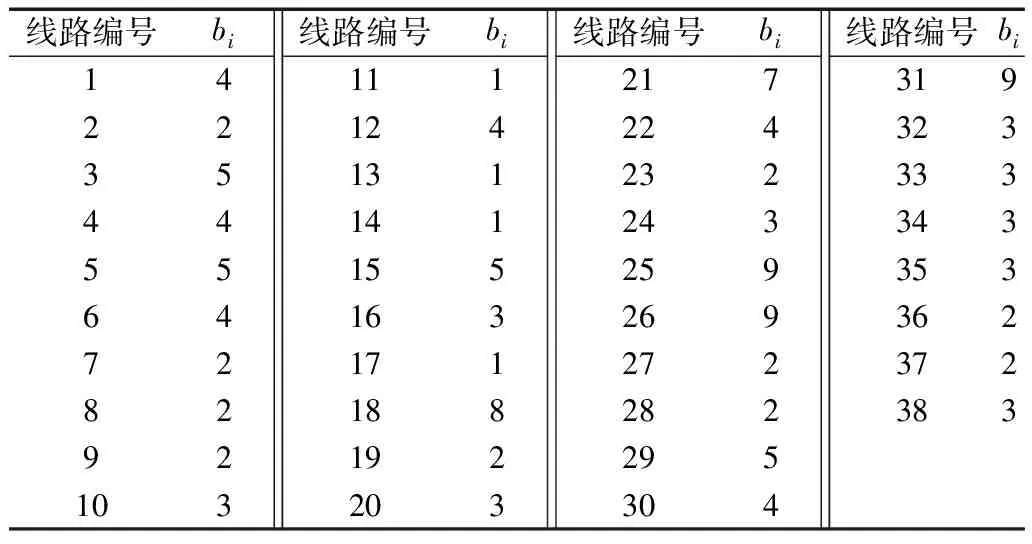
表3 各线路检修时长取值

根据2.2.1节单一线路检修风险内容,计算得出IEEE RTS-79系统各线路的Rsi,并将其归一化降序排列,结果如图6所示。

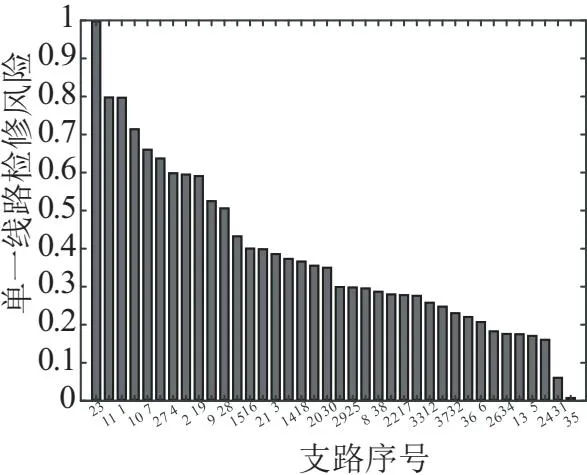
图6 单一线路检修风险值

4.2 算例分析

根据第2章可知,二进制决策变量X直接决定了F1、F3,且成为F2问题的约束。因此,采用二进制编码表示上层决策变量X,在解码时将X表示的检修任务作为参数,供下层问题利用求解器进行计算。灾时电网韧性评估采用蒙特卡洛算法,模拟次数N=1 000次。NSGA-II算法的参数设置如表4所示。

表4 NSGA-II算法参数

为了更好的比较支配关系,将三个目标值均进行归一化处理。输电网预防检修多目标多阶段优化模型的结果如图7所示。

图7 Pareto前沿分布

采用模糊隶属法对求得的最优前沿进行满意度排序,得出最优折衷解,如图7中实心圆点所示。按照各目标定义,分别取F1、F2、F3的极值得到极端解1与极端解2,如图7中阴影圆点所示。各点归一化后取值如表5所示。由表5可知,极端解1的F1最小,其F2、F3的值也为最小,表明当花费的预防检修费用最小时,预防检修期间风险最低,说明此时仅开展了小部分线路检修工作,但该方案韧性提升效果最差。极端解2的F3最大,其F2、F3的值也随之上升,表明韧性提升效果最优,但预防检修费用与预防检修风险将大幅上升。取最优折衷解可将三者兼顾,在有效提升韧性的同时,控制灾前阶段的费用与电网运行风险。

表5 极端解与最优折衷解取值

将未进行预防检修的系统记为方案1,最优折衷解方案记为方案2。记T0-T2这一阶段为输电网系统退化期望持续时间Td。将二者的灾时韧性指标进行对比,如表6所示。可以看出,经过输电网灾前预防检修,输电网韧性有较大增强,且缩短了输电网的退化持续时间,与未检修的方案相比,增强了输电网应对极端气象灾害的能力。

表6 不同方案的灾时韧性指标对比

最优折衷解对应的待检修输电线路以及灾前预防检修计划方案如表7所示。

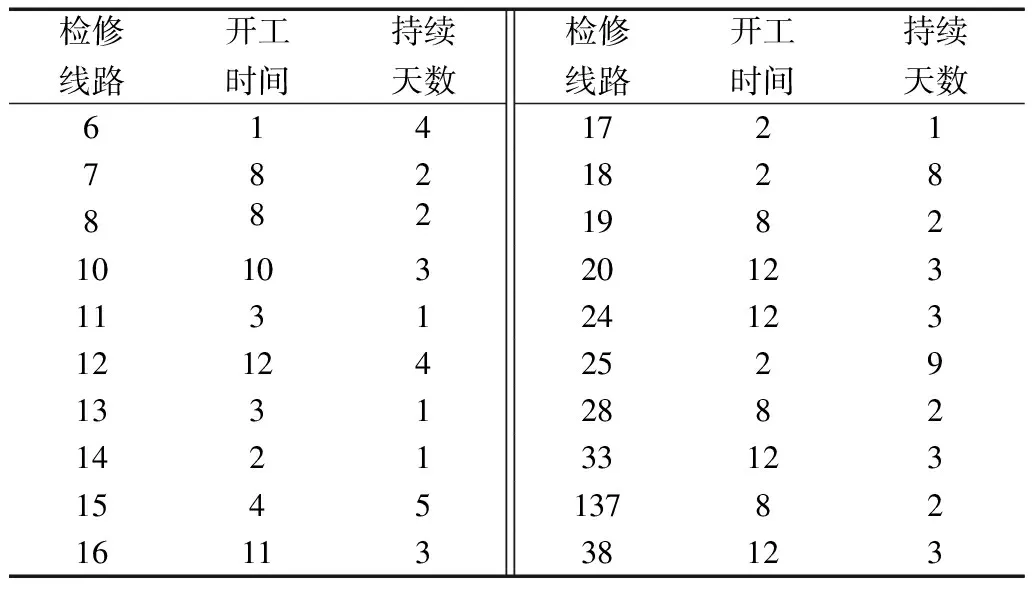
表7 灾前预防检修计划方案

由表7可以看出,灾前预防检修期间的15天内共有检修任务20项,该计划的单日最大重叠度仅为7。可以看出文中提出的检修重叠风险优化模型能够有效地降低检修任务的重叠时间,在检修任务较为密集时能够更加合理、科学地安排,降低电网运行风险。

5 结束语

针对输电网灾前预防阶段,文章从灾前预防检修的角度出发,首先建立了期望灾害风险抵御力输电网韧性评价指标。基于场景分析法以及蒙特卡洛模拟法,建立了考虑韧性提升的输电网灾前预防检修决策过程。以此为基础,建立了输电网灾前预防检修多目标多阶段优化模型。针对该模型维数高、包含子问题等特点,采用NSGA-II与数学求解器结合的求解方法。算例结果表明,所提模型与方法能得出合理的输电网灾前预防检修计划,在有效提升灾时电网韧性的同时能有效控制灾前检修计划费用以及灾前检修风险,对输电网应对极端灾害等事件具有一定指导意义。