不同海拔高度交流电晕电流脉冲特性实验研究

刘永聪,何旺龄, 2,刘兴发,何泽宇,蓝磊,鲁海亮

(1.武汉大学 电气与自动化学院,武汉 430072; 2.华北电力大学 电力工程系,河北 保定 071003; 3.电网环境保护国家重点实验室,武汉 430000)

0 引 言

我国地域辽阔,建设以特高压为骨干网架的坚强电网,可以实现跨区域、远距离、大功率的电能输送,这是我国国情与电力行业发展的必然选择。因此我国高压交流输电线路运行环境与国外大多数地区相比情况更加复杂,高海拔跨越问题便是我国交流输电技术面临的关键问题之一[1-2]。相对于平原来说,高海拔地区输电线路电晕效应问题更为严重[3]。

当海拔高度升高时,大气压强降低,空气密度减小,电子平均自由程增加,使得电子碰撞前所积累的能量增大,有效碰撞电离更容易发生,电晕放电现象更加剧烈,引发的电磁环境问题也更加严重[1,4-7]。高海拔条件下交流输电线路的电磁环境水平,已成为高海拔地区导线选型和线路结构设计的关键制约因素。因此有必要对电晕放电特性随海拔高度的变化规律开展更深入的研究,进一步明确海拔高度对电晕放电现象的影响机理。

近年来,针对高海拔电晕放电及电磁环境问题,国内学者开展了大量研究工作[8-9]。2007年,文献[10]首次计算分析了高海拔条件下1 000 kV交流输电线路的起晕电压和电晕损耗。2009年,文献[11]利用人工气候室研究了气压对导线直流电晕特性的影响,对电晕效应随气压的变化规律进行了定性的分析。同年,文献[12-13]在四个海拔高度获得了四种型号导线的交流起晕电压值,并提出了起晕电压的海拔校正公式。同年,唐剑等开展了交流电晕无线电干扰试验研究,得到了海拔高度对无线电干扰的影响特性[1]。2014年,文献[14]提出了更准确的高海拔地区交流导线起晕电压的海拔校正公式。2017年,文献[7]通过5个海拔高度点的实测数据拟合,提出了新的无线电干扰海拔高度修正系数。2018年文献[15]利用西宁市(2 200 m)的特高压电晕笼,获得了实际导线的电晕损失数据。

目前,低海拔地区导线电晕带来的电磁环境问题基本得以解决,而国外少有高海拔大跨越输电需求,因此对高海拔地区电晕效应研究较少[16]。上述国内现有研究大多针对高海拔地区真型导线电晕效应的外部特性,如起晕电压、电晕损耗、无线电干扰等数值进行计算分析、试验测量,提出针对特定型式导线的海拔修正方法。有必要从电流放电脉冲角度开展研究,进一步分析海拔高度对电晕特性的影响机理,为更加精细化、差异化地预测不同海拔高度下的电晕效应水平提供依据,提升高海拔地区特高压交流输电的经济性、可靠性和环保性。

文章利用可移动式小电晕笼及高频电流高电位采集系统,对5个海拔点的交流电晕电流脉冲数据、无线电干扰及可听噪声水平进行了实验测量,分析了海拔高度对电晕电流脉冲特性的影响,以及不同海拔高度下电晕电流脉冲同无线电干扰、可听噪声水平之间的关联关系,从而获得了海拔高度对交流电晕特性的影响规律。文章主要结论可为我国高海拔地区交流输电线路的设计及电磁环境水平预测工作提供一定的技术支撑。

1 可移动式小电晕笼实验

1.1 小电晕笼实验装置

文章利用可移动式小电晕笼及高频电流测量系统,在不同海拔高度下进行电晕放电实验。小电晕笼具有投资小、实验条件可控、结构调整方便、试验周期短等优势[11-12]。小电晕笼主要用于电晕放电相关的基础研究,通过设计合理的结构,电晕笼中细导线表面场强可以达到实际输电线路表面场强水平,用来模拟实际导线的电晕过程。

文章实验装置的各个部分均为可拆卸设计,以便用车辆运输至不同海拔高度点进行实验。在各海拔高度点对实验系统进行现场组装,实验布置如图1所示,其中,电晕笼的尺寸为直径0.4 m,长度1 m。

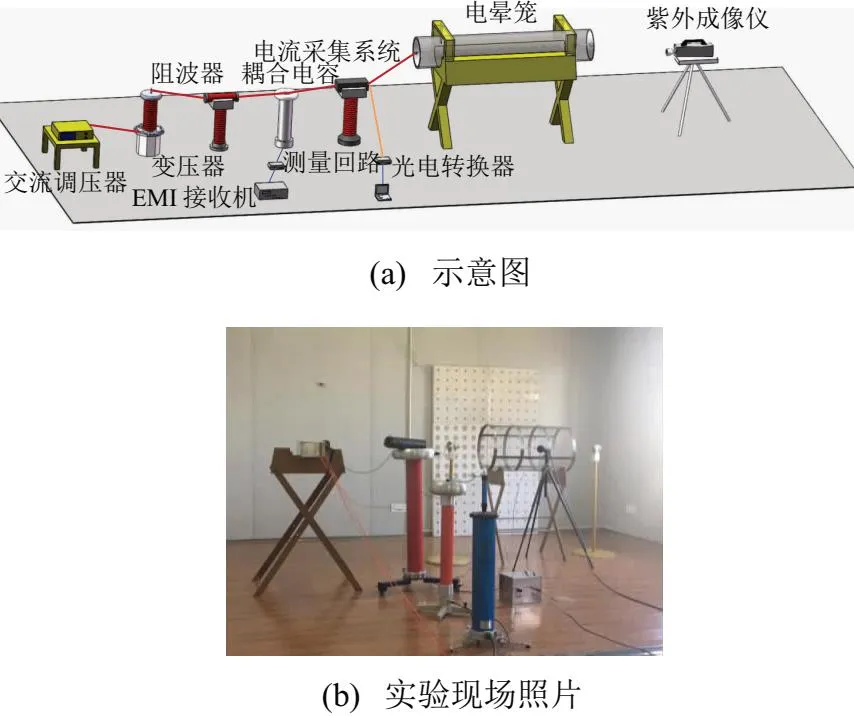
图1 实验布置图

处于电晕笼外部的导线,其终端会发生端部效应,使得导线终端的表面场强发生畸变,畸变处导线表面电场较大,电晕放电强烈,从而影响整个实验系统测量的准确性。因此实验中采用了在导线终端接入均压环的方法抑制端部效应。

1.2 测量系统与实验方法

文章实验所使用的高频电流高电位采集系统,通过光纤传输测量信号实现高、低电位之间的电气隔离,保证测量人员的安全。实验电路图如图2所示。

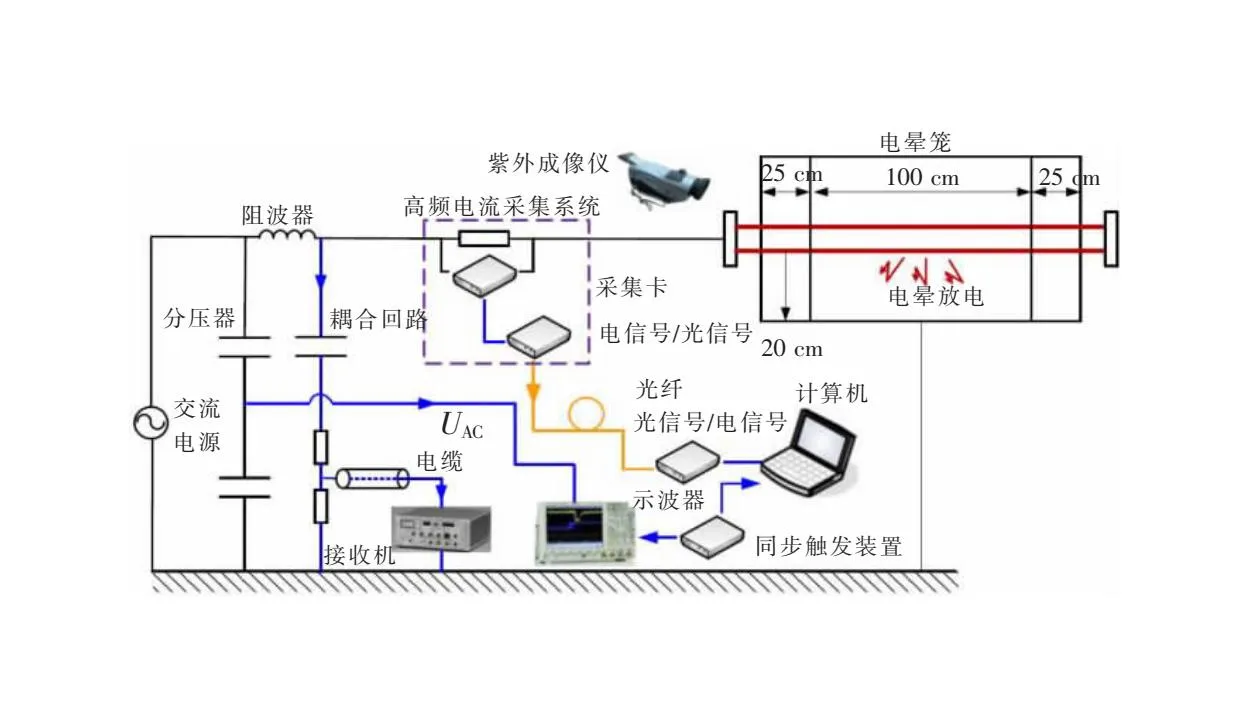
图2 实验电路图

为了准确测量交流电晕放电脉冲,电流传感器采用多个无感电阻同轴并联的方式,减小杂散电感的影响,提高电流传感器的上限带宽,电流传感器总阻值为400 Ω。测量装置利用高速采集卡采集导线的放电电流数据。电晕高频电流采集系统需分辨出最小上升沿小于10 ns的脉冲,单次采集数据应存储至少一个交流周期。因此,系统高速采集卡选用模块化示波器,带宽200 MHz,单通道采用频率为500 MSa/s,最小采样间隔为2 ns,存储深度为16 Mpts,单次可存储数据时长为0.032 s。

电晕放电是由导线表面较高的电场强度所导致,而电场强度可以通过施加电压来调节。文章实验导线选择为1 mm光滑细铜丝,施加交流电压有效值为：15 kV、20 kV、25 kV、30 kV和35 kV。在不同海拔高度、不同施加电压条件下,进行高频电晕电流、无线电干扰水平及可听噪声水平数据采集。

1.3 实验场地与测量条件

文章实验在湖北武汉、青海西宁、青海共和、西藏拉萨、西藏羊八井,海拔高度分别为20 m、 2 260 m、 2 840 m、3 660 m、4 320 m等五个测量点进行,重点获取高海拔地区的交流电晕特性。所有实验选择在室内场地进行,要求实验场所空间足够且周边环境安静,以尽量减小环境噪声对试验测量的影响。测量环境相对湿度维持在40%～60%,环境温度维持在20 ℃～30 ℃。

实验时将小电晕笼接地,对实验导线施加不同有效值的交流电压进行测量。通电后缓慢升压,通过电晕电流脉冲信号及紫外成像仪观测,判断导线表面的电晕放电状态。在导线起晕后,每隔5 kV同步记录1组数据,包括电晕电流脉冲信号、无线电干扰水平以及可听噪声水平。海拔高度较高时(3 000 m以上),导线施加电压达到30 kV以上,实验设备有击穿的风险,因此测量数据记录到30 kV为止。

2 不同海拔高度下电晕电流脉冲的测量结果及分析

2.1 电流脉冲数据处理方法

文章采集了不同海拔高度下电晕电流脉冲波形数据,采样间隔为4×10-9s,单次采样点数为1.25×107,波形时长为0.05 s。读取实验采集的数据后,对波形进行滤波处理,滤除测量系统噪声及交流基波信号。绘制电晕电流脉冲波形图,并统计分析不同海拔高度下电晕电流脉冲的特征参数。

导线施加电压为30 kV时,不同海拔高度下一个交流周期(0.02 s)内的电晕电流脉冲典型波形图如图3所示。

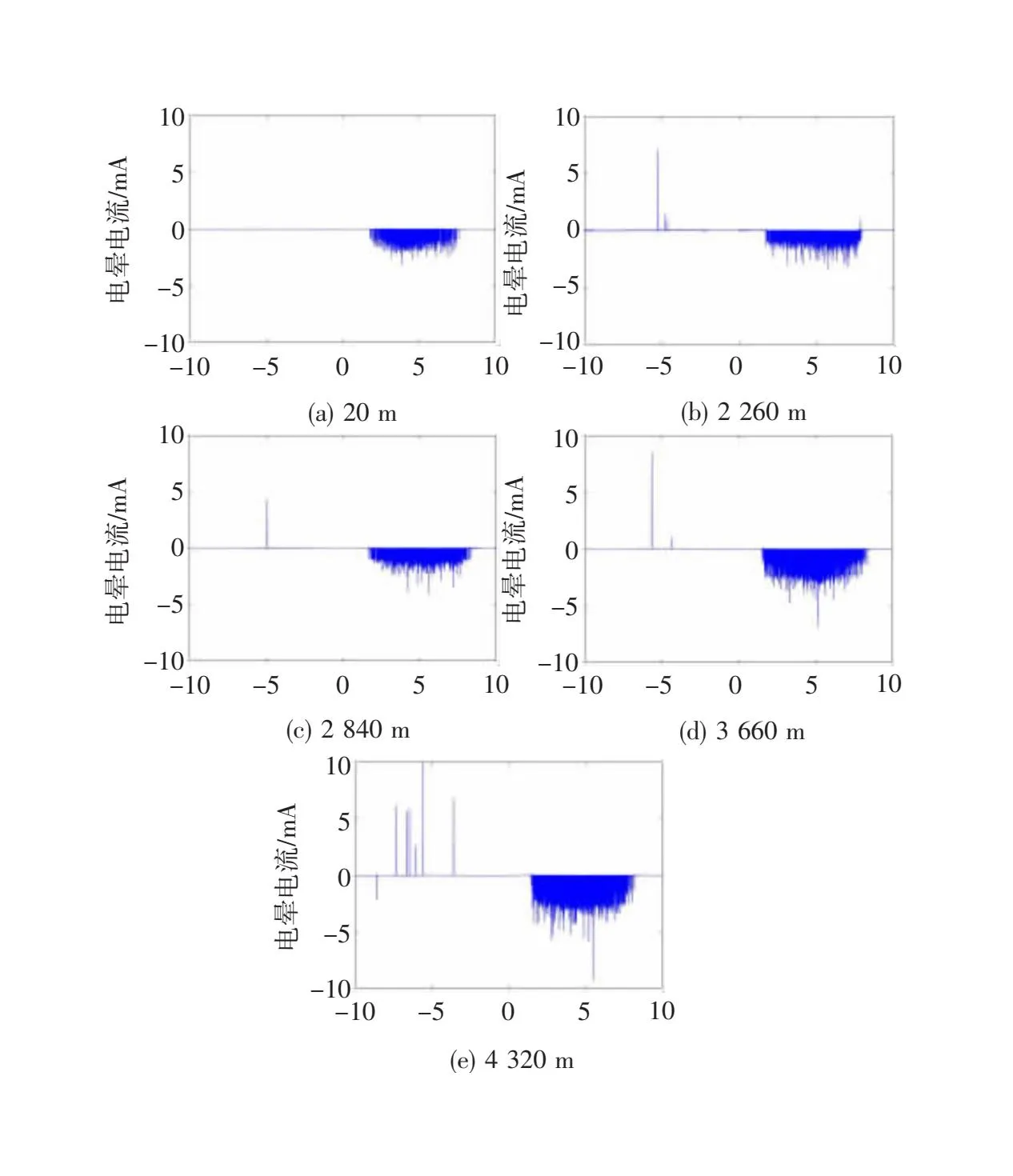
图3 不同海拔高度下电晕电流脉冲波形图

从图3可以看出,随着海拔高度的增大,交流正、负半周的电晕电流脉冲数量和幅值都有明显的增大。由于电晕笼中不均匀电场的极性效应,在相同施加电压与环境条件下,正极性比负极性起晕电压高,因此更容易观测到负极性电晕。同时由于正极性击穿电压较低,为了保证试验的安全性,不宜对导线施加过高的电压,因此测量到的正半周脉冲数量不多,但总体趋势和规律仍然可以从图3中直观地看出。

在每组脉冲波形数据中,均选取一个完整的正弦波周期(0.02 s)数据作为样本进行统计分析。脉冲幅值、单位时间的脉冲数量、幅值概率密度、间隔时间概率密度等是电晕电流脉冲的重要表征参数[17],与电晕效应密切相关,下面分别对它们进行统计分析。由于正、负极性电晕电流脉冲的特征参数、变化规律均不一致[18],在文章实验条件下测得的正极性脉冲数量较少,统计分析难以得出有效的规律性结论,因此后文主要对测量数据中交流负半周的负极性电晕电流脉冲特性进行统计分析。

2.2 电晕电流脉冲幅值及数量特征

文章实验对每个海拔高度及每个导线施加电压条件单独测量10次,即每个数据点对应10个样本,而后对不同海拔高度下电晕电流脉冲的幅值、数量及时间间隔等特征参数进行统计,总结分析海拔高度对交流电晕电流脉冲特性的影响规律。

在不同导线施加电压下,交流负半周电晕电流脉冲幅值平均值和单个周期脉冲数量随着海拔高度的变化曲线,如图4和图5所示。

图4 不同海拔高度下电晕电流脉冲幅值

图5 不同海拔高度下电晕电流脉冲数量

由图4和图5可以看出,海拔高度20 m施加20 kV电压时的电流脉冲幅值的样本方差很大,应为实验时设备调试问题导致的异常数据,剔除此数据后,电晕电流脉冲幅值和数量均随着海拔高度的增大而增大。在电晕放电理论的流体动力学模型中,影响电晕放电的主要参数汤森电离系数和吸附系数均与相对空气密度有关[19],海拔高度的增大会使气压p降低,相对空气密度d减小,电离系数a和吸附系数h增大,导致电晕放电脉冲形成和发展过程中的正离子、电子和负离子等微观粒子迁移的速度加快,宏观表现即为电晕脉冲的幅值和数量增加,时间间隔减小。

导线施加电压越高,连线斜率越大,说明电晕电流脉冲幅值和数量随海拔高度增加的幅度越大,这是因为导线施加电压的增大也有利于电晕的发生,从而使海拔高度的影响更为显著。另外,脉冲幅值在海拔高度3 000 m以下增幅较小,在3 000 m以上迅速增大,该现象在后文脉冲幅值概率分布特性分析中进行了解释,而脉冲数量随海拔高度的增加均匀增大。

2.3 电晕电流脉冲统计特性分析

为研究海拔高度的影响,取导线施加电压为30 kV时的数据,对不同海拔高度下的交流负半周电晕电流脉冲的幅值和脉冲时间间隔进行统计分析,绘制不同海拔高度下脉冲幅值和间隔时间的概率分布直方图如图6和图7所示。

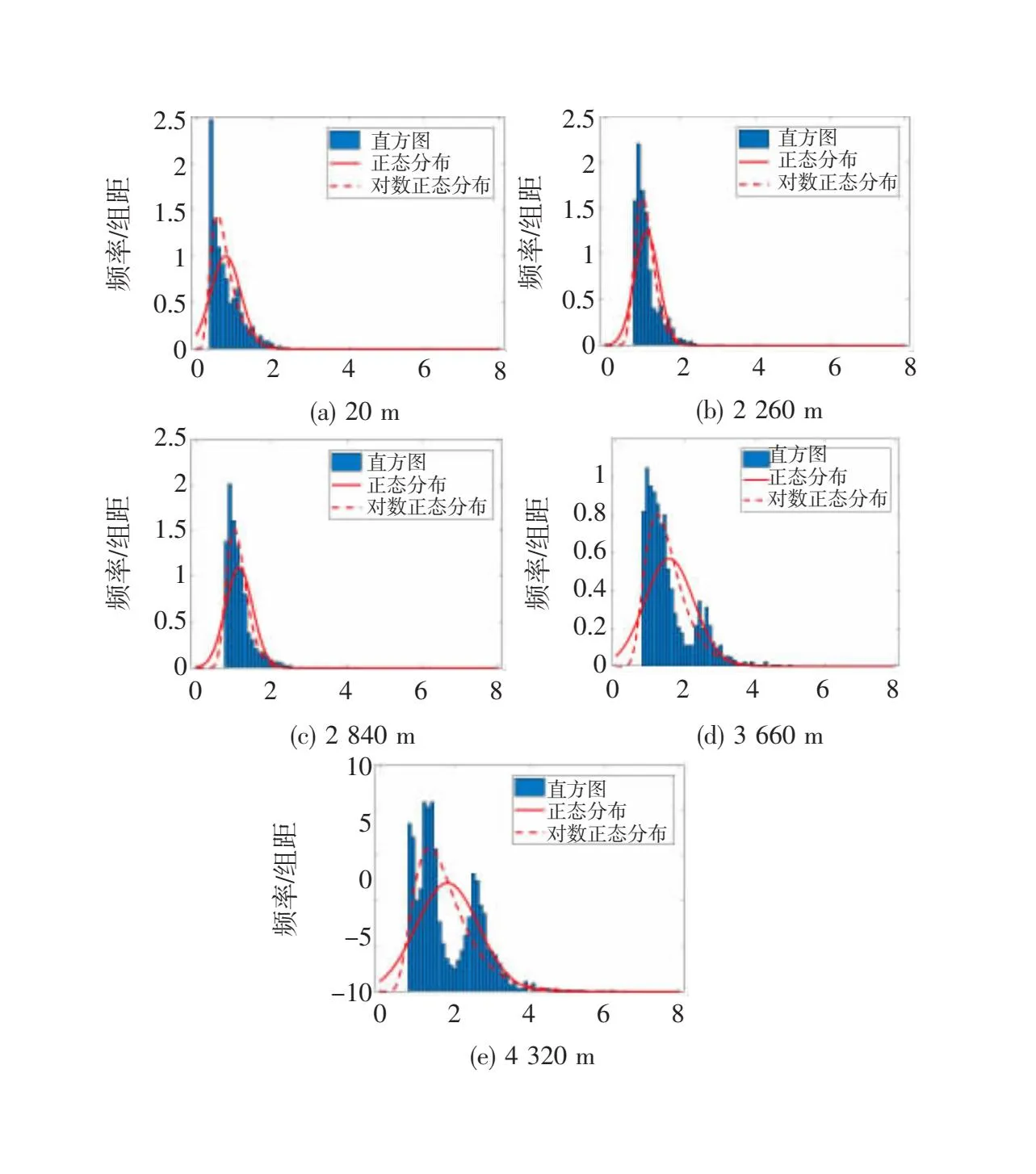
图6 电晕电流脉冲幅值概率分布直方图

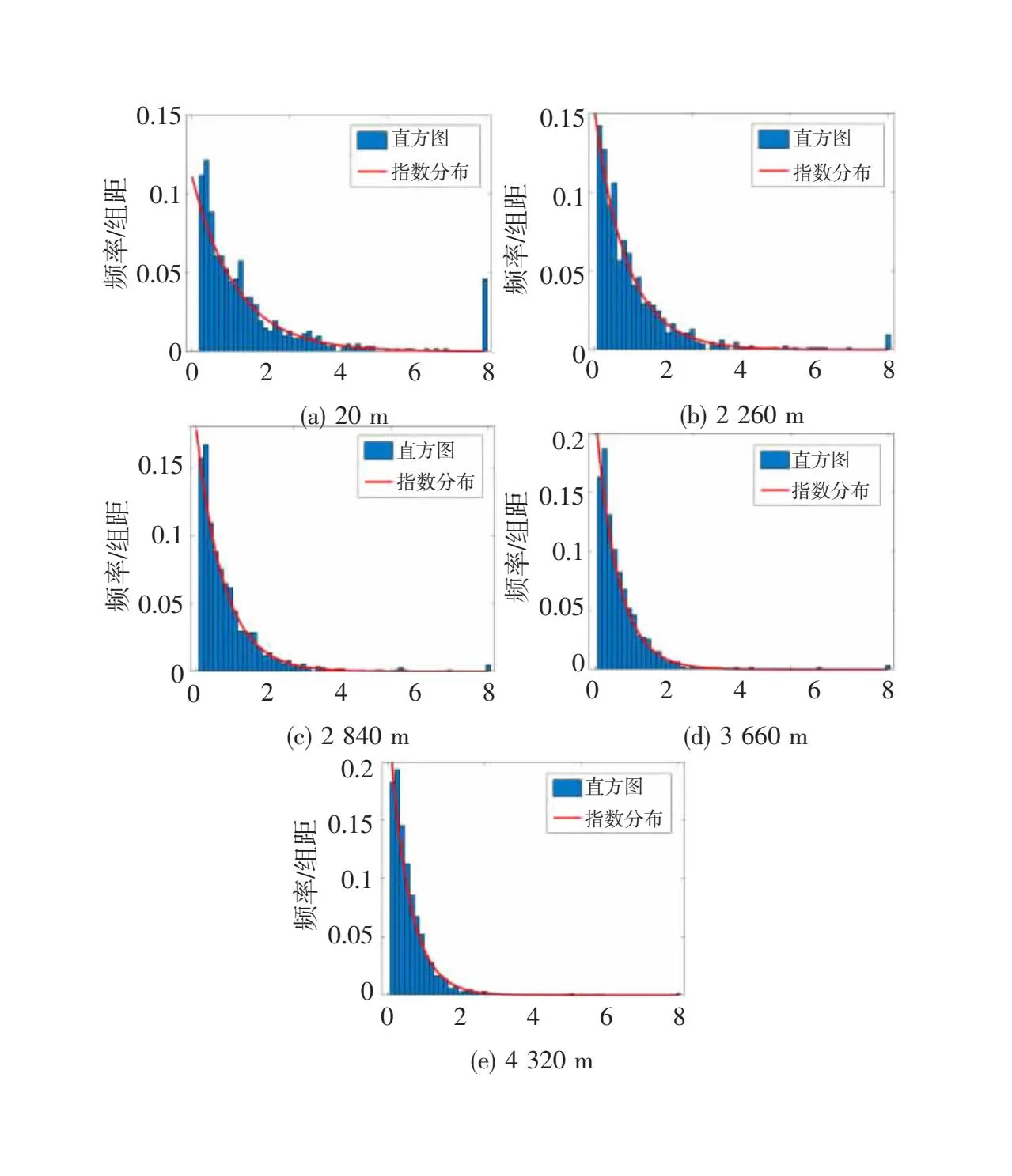
图7 电晕电流脉冲间隔时间概率分布直方图

由图6,电晕电流脉冲幅值概率分布与对数正态分布的密度曲线较为一致,海拔高度的增加使脉冲幅值的均值和最大值增大,同时使脉冲幅值概率分布更加分散,随机性增大。当海拔高度较低时(≤2 840 m),海拔高度的变化对于负半周电晕电流脉冲幅值概率分布的影响较小,脉冲幅值大多分布在1 mA～2 mA范围内;而当海拔高度≥3 660 m时,脉冲幅值出现了较大的部分,在2 mA～3 mA范围内出现了第二个概率分布峰,且随着海拔高度的继续增大,高幅值范围放电脉冲占比显著增加。这标志着,在高海拔条件下电晕放电出现了新的放电脉冲形态。这一部分幅值较大的脉冲,可能是导致高海拔地区无线电干扰和可听噪声等电晕效应进一步增强的原因。

由图7可知,电晕电流脉冲间隔时间分布呈现左高右低、指数衰减的趋势,与指数分布的密度曲线较为一致。在海拔高度20 m时,电晕电流脉冲的时间间隔最大值超过200 ms,分布的随机性很大。随着海拔高度的增大,当海拔高度达到2 840 m时,脉冲时间间隔的最大值减小至了80 ms左右,并且概率分布的随机性减小,分布更为集中。随着海拔高度增大,电晕电流脉冲间隔时间减小,分布的随机性也明显减小。

2.4 海拔高度与电晕电流脉冲有效值的关系

文章研究发现,电晕电流有效值包含了导线施加电压、交流电晕电流脉冲幅值、数量等信息,采用电晕电流有效值作为特征量可以更全面准确地表征电晕电流脉冲与电晕效应之间的关系。因此将电晕电流有效值作为中间变量,进一步研究海拔高度对交流线路电晕效应的影响。

对电晕电流脉冲数据进行处理,计算交流一个周期内的电晕电流有效值IRMS(均方根值),结果如表1所示。

表1 交流一个周期内电晕电流有效值(单位：mA)

(1)

式中IRMS为电晕电流有效值,单位mA;T为一个交流周期0.02 s,单位s。

表1的每一列为在同一海拔高度,不同导线施加电压下的电晕电流有效值数据。作图可以得到在各个海拔高度下,电晕电流有效值均随导线施加电压的增大而增大,且电晕电流有效值与施加电压呈线性增长关系。对二者进行线性拟合,结果如图8所示。

图8 不同海拔高度下电晕电流有效值与施加电压的线性拟合

经统计分析得到,该线性拟合曲线簇的斜率k,截距b均为海拔高度h的函数。

I=k(h)U-b(h)

(2)

式中I为电晕电流有效值,单位μA;U为导线施加电压,单位V。

对线性拟合曲线簇参数k、b与海拔高度h的关系曲线进行拟合,如图9所示。

图9 参数k、b与海拔高度h的三次函数关系

得到两者呈三次函数关系。

(3)

式中h为海拔高度,单位km。

至此,文章得到了电晕电流脉冲有效值随海拔高度的变化关系。为了进一步获得海拔高度对交流电晕效应的影响机制,下文对不同海拔高度下电晕电流脉冲有效值与无线电干扰和可听噪声水平的关系进行研究。

3 电晕电流脉冲与无线电干扰和可听噪声的关联关系

3.1 电流脉冲与无线电干扰的关系

以电晕电流有效值和0.5 MHz无线电干扰水平为特征量,分析不同海拔高度下电晕电流脉冲与无线电干扰水平的关系。不同海拔高度下,无线电干扰水平与电晕电流脉冲有效值的关系,如图10所示。在各个海拔高度下,无线电干扰水平均随电晕电流的增大而增大,且总体呈现对数增长关系。

图10 无线电干扰水平与电晕电流有效值的关系

图10中,在各个海拔高度下,无线电干扰水平随电晕电流的增长趋势均一致,且不同海拔高度数据杂乱分布,连线相互交叉,海拔高度对二者之间的关联关系并无显著影响。进一步对无线电干扰水平与电晕电流有效值进行函数拟合,从而定量分析两者的关系。

文章利用多种函数模型,对无线电干扰水平与电晕电流有效值的关系曲线进行拟合,根据拟合效果评价指标最终选择对数函数模型作为最优拟合,结果如图11和表2所示。

表2 无线电干扰水平与电晕电流有效值函数拟合结果

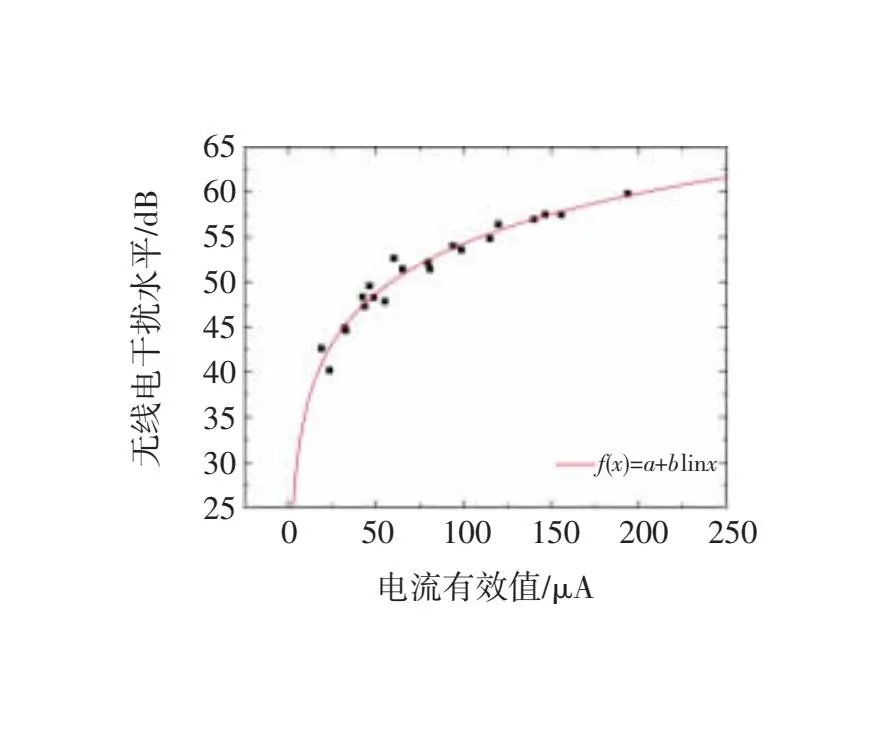
图11 无线电干扰水平与电晕电流有效值的拟合曲线

f(x)=a+blnx(x>0)

(4)

表2中,a、b分别为函数模型最优拟合曲线的参数值;RMSE为拟合标准差,值越接近0,表明模型对数据拟合的越好;R-square为确定系数,取值范围为[0,1],值越接近1,表明方程的自变量对y的解释能力越强。

综上所述,可以得到电晕电流脉冲与无线电干扰水平的函数关系,即无线电干扰水平V(dB)与电晕电流有效值I(μA)大致呈对数增长关系：

V=17.35+8.02ln(I) (I>0)

(5)

将式(2)和式(3)代入式(5),即可得到无线电干扰水平随海拔高度的变化关系。

3.2 不同海拔高度下电流脉冲与可听噪声的关系

以电晕电流有效值和A声级可听噪声水平为特征量,分析不同海拔高度下电晕电流脉冲与可听噪声水平的关系。不同海拔高度下,无线电干扰水平与电晕电流脉冲有效值的关系,如图12所示。在各个海拔高度下,无线电干扰水平均随电晕电流有效值的增大而增大,且均呈现对数增长关系。

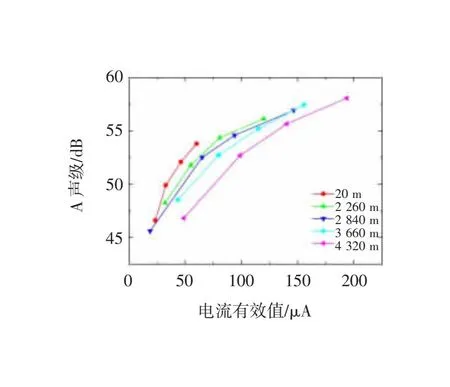
图12 可听噪声水平与电晕电流有效值的关系

观察二者关系曲线的主要部分,在不同海拔高度下,可听噪声水平随电晕电流有效值的增长趋势均一致,但随着海拔高度的增大,关系曲线逐渐旋转并右移。

电晕放电过程中,电子和离子与空气分子发生非弹性碰撞,将能量传递给空气分子,引起空气分子的振动,产生脉冲声波。空间可听噪声就是脉冲声波通过空气分子振动传播的结果[20]。因此,海拔高度升高,空气的相对密度减小,影响了可听噪声的传播过程,导致可听噪声水平与电晕电流脉冲的关联关系随海拔高度改变。而无线电干扰为一种电磁波信号,其传播不受空气相对密度变化的影响,因此各海拔高度下无线电干扰水平与电晕电流脉冲的关联关系一致。

分别对不同海拔高度下可听噪声水平与电晕电流有效值进行函数拟合,从而定量分析两者的关系以及海拔高度的影响。根据图12中各海拔高度数据点的分布及连线趋势,选择对数函数模型对数据进行拟合,结果如表3和图13所示。

表3 不同海拔高度下可听噪声水平与电晕电流有效值函数拟合结果

图13 可听噪声水平与电晕电流有效值的拟合曲线

为了揭示海拔高度对可听噪声水平与电晕电流有效值关系的影响,首先对全部数据点进行拟合,然后采用保持函数模型参数a、b中的一个不变,来分别拟合不同海拔高度下另一个参数的方式,揭示关联函数的参数随海拔高度的变化情况,如表4所示。

表4 可听噪声水平与电晕电流有效值对数函数拟合结果

根据表4中拟合结果,可以看到单独对a、b进行拟合时,随着海拔高度的提升,a、b的值均呈现减小趋势,相应对数关系曲线逐渐旋转并右移。如图13所示,随着海拔高度的提升,对数关系曲线逐渐旋转并右移,与对数据初步分析的结果一致。

综上所述,可以得到电晕电流脉冲与可听噪声水平的函数关系,即可听噪声水平A(dB)与电晕电流有效值I(μA)大致呈对数增长关系：

A=29.88+5.347ln(I) (I>0)

(6)

海拔高度对二者关系的影响为,随着海拔高度的升高,对数函数关系的系数a、b会逐渐减小,关系曲线逐渐旋转并右移。

将式(2)和式(3)代入式(6),即可得到可听噪声水平随海拔高度的变化关系。

4 结束语

文章利用可移动式小电晕笼装置在5个海拔高度点进行了交流电晕特性实验,对不同海拔高度下电晕电流脉冲、无线电干扰与可听噪声数据进行了采集。在文章实验条件下,通过对采集数据的分析,得到如下结论：

(1)随着海拔高度升高,交流电晕电流脉冲的幅值平均值增大,同时幅值的概率密度分布逐渐分散,随机性增大。在海拔高度大于3 000 m时,幅值概率分布在较大的2 mA～3 mA范围出现了第二个峰,导致脉冲幅值平均值在3 000 m以上迅速增大;

(2)随着海拔高度升高,一个周期内交流电晕电流脉冲的数量增加,相邻脉冲之间的时间间隔减小,且时间间隔的概率分布逐渐集中,随机性减小,脉冲形成时间变得更加规律、均匀;

(3)采用电晕电流有效值作为特征量可以更全面准确地表征电晕电流脉冲与电晕效应之间的关系。电晕电流有效值与导线施加电压呈线性函数关系,该线性函数的斜率k、截距b为海拔高度h的三次函数;

(4)在不同海拔高度下,无线电干扰水平均随电晕电流的增大而增大,且无线电干扰水平与电晕电流有效值呈对数增长关系。不同海拔高度下二者的增长关系特性没有明显区别;

(5)在不同海拔高度下,可听噪声水平均随电晕电流的增大而增大,可听噪声水平与电晕电流有效值呈f(x)=a+bln(x)形式的对数增长关系。且随着海拔高度的增大二者函数关系的系数a、b的值逐渐减小,相应关系曲线逐渐旋转并右移。