蜿蜒步态下的蛇形机器人路径跟踪控制研究

乔海晔，吴清辉，张震

（1.佛山职业技术学院，佛山广东，528137；2.广州市威控机器人有限公司，广州广东，510500）

1 项目综述

2012 年，美国卡内基梅隆大学开发的Uncle Sam 蛇形机器人。该机器人引入了柔顺控制，使得其运动特性更加贴近生物蛇，且其关节采用正交连接，每个关节都装有一个电机，使得其能做出更为复杂的运动，并很好的实现了攀爬及翻越能力[1]。目前，将多足机器人与蛇形机器人投入实际救援行动的应用不多，大部分还处在实验室环境下的研究阶段[2]。蛇形机器人特殊的肢体结构和运动原理使其机体的运动控制与路径跟踪存在着极大的挑战，是蛇形机器人领域的研究热点之一。

蛇形机器人在蜿蜒步态下的路径跟踪控制问题，首要任务是控制蛇形机器人的运动方向。Hirose 首先为蛇机器人引入了一种旋转行为，通过在曲率上增加一个恒定的偏移量来增加体波[3]。通过调节这个恒定的偏移量，机器人就能够进行转向，这种方法称为“偏移转向”。后续的工作证明了偏移转弯在二维蛇机器人运动问题中的有效性。叶长龙通过幅值调整、相位调整等方法改变蛇形机器人蜿蜒运动的运动方向，并在幅值调整法中进行了初步的定量转弯半径和转弯角度的研究[4]。Dai 等人使用几何力学的技术，将微分几何应用于刚体运动，来设计一种使原地转弯成为可能的步态，这种方法称为“几何转弯”[5]。这两种平面内的转动行为都是通过沿机器人体传播一个行波并调制行波的参数来实现的。Wang 等人受微小线虫线虫行为的启发，提出了一种新颖的无肢机器人原地转弯步态[6]。为了简化机器人内部自由度的控制，引入了一个受生物启发的模板，其中两个共面行波叠加产生一个平面内旋转运动，即欧米伽旋转，使得机器人能够在高度受限的空间中转弯。实现蛇形机器人跟随期望路径的次要任务是使蛇形机器人根据期望路径调节运动方向。

在进行目标识别或追踪任务时，常常会因头部关节摆动幅度过大而导致前方目标丢失。因此如何保证蛇形机器人在蜿蜒运动下的头部稳定成为实现定向运动的首要目标。2016 年，来自新西兰的研究者 Pinwei Jin 和 ChiKit Au 提出了一种头部固定的方法[7]，重新设计机器人头部关节的控制函数，通过添加补偿函数的方式使机器人头部在运动过程中始终朝向一个方向，即分段控制。而该方法的缺陷在于补偿函数的参数确定方法较为复杂，且蛇头与整体之间并不连贯，需要对头部舵机进行单独的函数控制。而在机器人蜿蜒步态控制器设计领域同样存在诸多成果。2017 年，来自日本的学者Ryo Ariizumi 针对无侧滑约束的蛇形机器人设计了头部位置控制器[8]，应用于头部轨迹导航控制。文章分析了各向同性摩擦力时机器人的运动情况，并认为奇异状态下的机器人具备可操作性，是进行控制的关键。但是对于摩擦是各向异性时的情况仍缺乏讨论[9]。

2 蛇形机器人技术特点

面对灾后复杂狭窄空间，蛇形机器人因其狭长形态和灵活的运动能力，能够实现对管道等狭窄空间的搜索，弥补了足式机器人无法探测到狭窄空间的缺点。不同于轮式或者足式机器人具有独立地推进机构，蛇形机器人由于其关节和连杆耦合度高，驱动机构需同步整个机体的运动，因此蛇形机器人的控制设计是极具挑战性的[10]。在路径跟踪控制中，蛇形机器人的质心位置在前向蜿蜒运动中并不是直线运动，而是周期性地在前向直线附近摆动，除此，方向角也在直线附近周期性摆动，仅靠传统路径跟踪控制方法将其状态控制到理想直线路径下是无意义的，因此蛇形机器人轨迹跟踪控制难度较大[11]。

直线路径跟踪控制是实现机器人沿指定路径移动并进行三维重建的前提。通过基于滑模控制理论的直线路径跟踪控制技术，减小了蛇形机器人在稳态运动时的误差。头部控制是保证传感器及相机数据稳定的基础。基于补偿函数的头部控制方法，提高了图像及传感器信息的稳定性和准确性。此基础上研究转弯方法，可以提高蛇形机器人避障效率。

3 蛇形机器人自适应运动控制技术

■3.1 基于滑模控制理论的直线路径跟踪控制技术

蛇形机器人基于滑模理论的轨迹跟踪控制技术路线图总结如图1 所示。

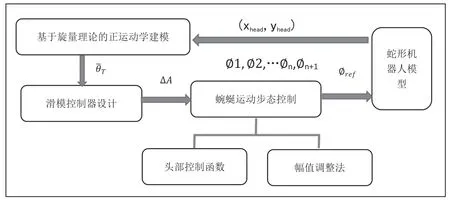
图1 基于滑模理论的轨迹跟踪控制技术路线图

以沿着全局x轴正方向运动为例，直线路径跟踪控制器的具体目标是机器人初始时刻处于任何姿态下，经过有限的时间后均能沿着全局x轴正方向运动。设定蛇形机器人的质心全局位置坐标为(p x,py)，前进的方向角为θ。所以控制目标即为py和，使得它们最终收敛于py=0，=0的极限环。

根据转弯角和控制参数ΔA之间存在定量关系，可以通过转弯实现机器人的定向运动。

学生通过观看Lagrange定理微视频自学，教师要及时追踪学生在线自测的反馈信息，并收集学生的疑惑、不理解的公式及证明的推导等。这节课的疑惑是Lagrange定理的证明中辅助函数的构造。在课堂上重点讲解难点疑惑，对于这节课，重点和难点是构造辅助函数对Lagrange中值定理的证明，可以多花点时间。

下面进行滑模控制器的设计。

选取蛇形机器人控制系统的切换面如下：

由于蛇形机器人系统可能存在远离滑动模块的情况，所以选用幂次趋近律公式作为本系统的趋近律。

由上式可得：

所以蛇形机器人的控制率公式如下：

滑模控制器，即方向控制器具体控制框图如图2 所示。

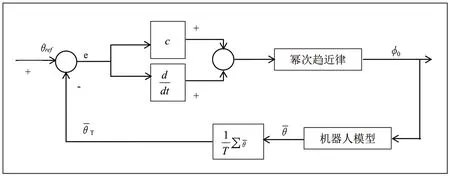
图2 基于滑模控制理论的方向控制器

为了验证上述控制器的稳定性。取李雅普诺夫函数V=s2/2，取V≥ 0。可得V˙=ss˙。结合幂次趋近律公式得：

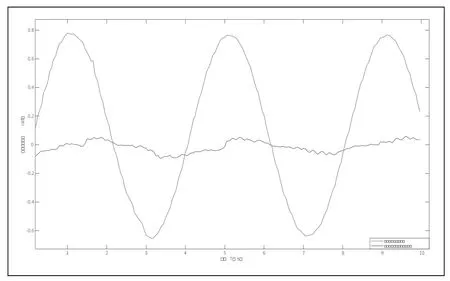
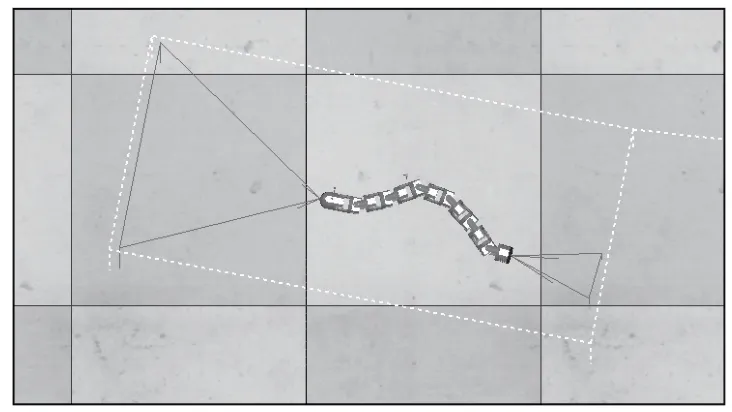
由于幂次趋近律公式中设定了k>0.1，0

■3.2 基于补偿函数的头部控制技术

引入补偿函数：

使得：

■3.3 基于头部稳定的转弯技术

在保证了蛇头稳定的基础上，蛇形机器人通过安装在头部的红外传感器来检测其前方是否有障碍物，当在前进方向中遇到障碍物时，蛇形机器人基于幅值调整法来改变其运动的幅度，从而达到控制机器人蜿蜒运动中避开障碍物的目的。

基于幅值调整法的蛇形曲线如图3 所示，其基本思想是通过调整幅值ΔA，来改变机器人的运动方向，从而实现转弯。其中幅值角和转弯角存在定量关系，φ=a2-a1=2aΔA,a1≈a(1-ΔA),a2≈a(1+ΔA)。

为保证蛇头固定，基于补偿函数的思想，蛇头部分的控制函数为：

所以基于头部控制的转弯控制函数如下式，假设奇数关节为俯仰关节，偶数关节为偏航关节。

4 仿真平台运动控制实验

蛇形机器人基于VREP 仿真平台的运动实验结果如下：

■4.1 基于补偿函数的头部控制实验

对蛇形机器人蜿蜒运动进行头部控制仿真，现期望蛇头运动方向与x 轴平行，其仿真实验图如图4 所示。

可以发现，上述实验蛇形机器人头部摄像机读取的信息非常稳定，由此可见蛇头部分得以很好的控制。对比没有头部控制下的蛇头运动方向角，如图5所示，可以发现，基于补偿函数的控制方法使得头部运动的稳定性大幅度提高。

图5 有无头部控制下的头部运动方向角对比图

■4.2 基于头部控制下的转弯实验

基于上述头部控制方法，本项目利用Vrep 进行蜿蜒运动时转弯的仿真实验，其转弯过程仿真图如图6 所示。

图6 基于幅值调整法的转弯仿真实验图

令蛇形机器人从全局坐标系原点出发，沿x轴正方向运动，并设定控制参数A=40°,K=60°，W=50°/s。在t∈[20,40]时，ΔA=10°，而在t∈[80,120]时，ΔA=-2 0°，其余时刻ΔA均为0。得到的仿真结果如图7 所示。

图7 基于幅值调整法的转弯仿真结果图

由上述结果可以发现，蛇形机器人转弯角度比较连续，且更好地维持了蜿蜒时的波形曲线。

■4.3 基于滑模控制的直线跟踪控制实验

利用Vrep 进行仿真实验，令蛇形机器人初始时刻质心坐标为（0，-5m），方向角为θ=45°，最终得到的运动仿真结果如图8 所示。

图8 基于滑模控制的机器人运动曲线

由上述仿真结果得，机器人在80s 左右达到稳态，且方向角在零附近波动，则本项目设计的控制器合理。并将本项目设计的滑模控制器与传统PI 控制进行对比，在机器人稳定达到预期直线后，机器人质心Y 坐标与期望值之间的误差结果见表1。可发现，与PI 控制相比，滑模控制的精确度更高。

表1 滑模控制与PI控制误差对比

5 结果验证

蛇形机器人自适应运动控制已在VREP仿真和实体上得到实现，并将其应用于蛇形机器人管道探测中，仿真和实体运动场景如图9 所示。

图9 蛇形机器人基于蜿蜒运动的管道探索仿真和实物运行图