定中和驱动一体化的超导转子驱动方法*

张源 胡新宁† 崔春艳 崔旭 牛飞飞 黄兴 王路忠 王秋良

1) (中国科学院电工研究所,北京 100190)

2) (中国科学院大学电子电气与通信工程学院,北京 100049)

3) (中国科学院赣江创新研究院,赣州 341119)

1 引言

高速旋转的转子具有定轴性,利用此特性可制作角速度或角位置传感器.超导转子磁悬浮装置利用超导体的完全抗磁性实现超导转子的悬浮,此时超导转子几乎可在没有能量损失的状态下,旋转和移动[1–6],故其可以获得极高的转速且实现稳定旋转.超导低温下材料的膨胀低、蠕变小、化学活性低,故超导转子磁浮装置制成的角速度传感器具有极高的精度潜力[7,8].美国通用电气公司从20 世纪60 年代就报道了超导转子磁悬浮装置样机的研究,且其测量精度是0.005 (°)/h[9],美国喷气推进实验室也对超导转子磁悬浮样机进行了研制,其样机精度可达到0.013 (°)/h[10].

超导转子的质量偏心和球面误差是影响超导转子测量误差的主要因素[11].超导转子结构越复杂,越难加工和装配出质量偏心小和球面误差小的超导转子.而超导转子的结构主要由其驱动电磁结构限制.已报道的精度最高的是美国通用电气公司设计制作的超导转子磁悬浮装置样机[12],其制作的样机均是采用了定子线圈驱动,力矩器线圈定中.而且都采用了转子内开圆柱孔的结构,然后定子和力矩器置于其中(I 号模型和II 号模型),或只力矩器置于圆柱孔(0 号模型)的形式.此超导转子驱动装置的超导转子结构和电磁驱动结构复杂,很难实现高精度的加工和装配,这限制了超导转子磁悬浮装置测角精度的进一步提升.基于此,本文设计了一种定子线圈置于转子外部的超导转子驱动电磁结构,定子线圈同时具有驱动和定中的作用.此结构的超导转子是一个完整对称的封闭结构,且转子球不存在理论质量偏心.与通用电气报道出来的超导转子驱动电磁结构相比,简化了超导转子的结构和驱动电磁结构,故此驱动电磁结构具有更高的精度潜力.本文主要针对此电磁驱动结构的设计进行了分析.

文献[13–15]基于有限元方法研究了定子线圈产生的磁场对超导转子的驱动力矩作用,并给出了对应的控制策略.文献[16]通过有限元方法和实验研究了定子线圈对超导转子的驱动力矩,并给出了有限元方法与实验的误差.本文在此基础上进一步通过有限元方法,分析了所设计超导转子驱动结构的定子线圈对超导转子的定中和驱动作用,提出了一种定中和驱动一体化设计的驱动方法,最后对所设计驱动方法的驱动效果进行了评估.分析结果为超导转子磁悬浮系统的设计、优化和超导转子驱动效果的评估提供参考

2 超导转子驱动结构设计

超导体具有完全抗磁性,因为磁场中的超导体会在其表面产生屏蔽电流,屏蔽电流产生的磁场抵消了进入超导体内部的磁场,所以磁场无法穿透超导体.而屏蔽电流产生的磁场也与超导体外部磁场发生作用产生了迈斯纳力,即迈斯纳效应.由于迈斯纳效应,磁场中的超导体受到垂直其表面的磁压力,磁压力的大小与超导体表面磁场模值的平方成正比[17].

式中,dF是作用在超导转子表面微元dS的迈斯纳力,B是表面微元dS的磁场,μ0是真空磁导率.

若超导转子表面是完整球面,转子球受到的迈斯纳力均过球心,此时迈斯纳力无法对转子球产生转矩.故定子线圈置于超导转子外部时,超导转子驱动结构采取了在转子赤道处切削平面的方式.综合考虑超导转子的对称性和加工难度,本文主要考虑了超导转子赤道四切面和八切面两种方案,如图1.

首先分析超导转子四切面和八切面的驱动力矩.理论上说定子线圈数量越多,超导转子的驱动效率越高,但实际装配难度越大,控制电路越复杂.所以考虑到实际的装配条件,以及为了使定子线圈产生的磁场充分作用在转子切削面上,定子线圈设计为四个盘型线圈,其和超导转子的位形如图2.由结构的对称性可知,四切面超导转子的驱动角周期是90°,驱动角周期指超导转子绕竖直轴旋转时,对应驱动力矩的变化周期.则八切面超导转子的驱动角周期是45°.

图2 超导转子四切面和八切面的驱动结构图Fig.2.Structure of four cutting planes and eight cutting planes of superconducting rotor.

接下来计算不同切削深度d的情况,超导转子切面深度示意图如图3.本文主要通过有限元方法对超导转子的磁力矩进行计算,即基于矢量磁势A方程在有限元软件Ansoft 对超导转子驱动系统进行建模分析[2,3].其中超导体的相对磁导率设置10–7,电导率设置10–7;远大于所建模型计算域设置Dirichlet 边界条件,其他边界条件设置自然边界条件.然后通过有限元软件Ansoft 模拟定子线圈同时通电,四切面超导转子和八切面超导转子绕竖直轴旋转90°的驱动力矩,如图4 和图5.其中超导转子的半径25 mm,定子线圈外径10 mm,内径6 mm,厚度3.9 mm,定子线圈中心到转子球心距离是28.15 mm.图4 表明在驱动过程中,四切面超导转子在d＞ 0.4 mm 以后,随切削深度d增加,超导转子的驱动力矩和驱动力矩的作用范围逐渐增大,“死区”逐渐减小.“死区” 是指在一个连续的角位置区间,其驱动力矩方向反复变化且大小接近零.但四切面的超导转子切削深度2 mm 后,其在角位置40°—50°的范围仍然存在“死区”,“死区”的存在是不利于超导转子的启动的.八切面超导转子在d>0.4 mm 以后,在整个驱动角区间不存在“死区”,如图5.所以从超导转子启动来说,八切面超导转子的驱动性能优于四切面超导转子,所以超导转子设计为赤道八切面结构.

图3 超导转子切削深度示意图Fig.3.Schematic of cutting depth of superconducting rotor.

图4 四切面不同切削深度下的驱动力矩Fig.4.Driving torque under four cutting with different d.

图5 八切面不同切削深度下的驱动力矩Fig.5.Driving torque under eight cutting with different d.

超导转子在驱动时,施加一个方向的力矩,以此维持其加速或者减速过程,一个驱动角周期中其有效的驱动力矩范围是半周期,故可用半个周期的平均驱动力矩来评估超导转子的驱动效果,如图6.在切削深度d≤ 1.6 mm 时,八切面方案的驱动效果大于四切面方案,切削深度d继续增大,四切面方案的驱动效果可超过八切面方案的驱动效果.但超导转子的切削深度d越大,对转子球面的破坏越大,且加工难度越大.故综合超导转子的“启动”要求和驱动效果,选择八切面方案.八切面超导转子在d=1 mm 以后随着切削深度的增加,平均驱动力矩开始缓慢增加,到d=1.2 mm 平均驱动力矩达到最大值.综合考虑,超导转子的切削深度d设置为1 mm.

图6 四切面和八切面的平均驱动力矩对比Fig.6.Comparison of driving torque of rotor with four cutting surfaces and those with eight cutting surfaces.

超导转子驱动装置除超导转子和定子线圈,还包括超导球腔和悬浮线圈.悬浮线圈和超导球腔完成对超导转子的悬浮功能,并形成一定的刚度.整形铌块和转子采用的是纯度99.5%的高纯铌,其下临界磁场0.14 T,临界温度9.12 K[18];铌钛合金超导体在4.2 K 时临界磁场近似11 T.铌钛线的临界磁场有足够裕度,故在驱动结构设计时主要考虑金属铌球表面临界磁场的限制.

超导转子的详细结构如图7,转子是由上、下两个半球壳组成的赤道加厚的空心薄壁球,转子质量84 g,极轴转动惯量3.72×10–5kg·m2,半径为25 mm,切除平面圆的直径14 mm.

图7 超导转子结构图Fig.7.Superconducting rotor structure.

3 超导转子驱动结构的转矩分析

3.1 超导转子驱动转矩分析

定子系统采用四个定子线圈串联,通过光纤传感器检测转子切削面相对定子线圈的位置,然后对定子线圈电流的通断进行控制,从而实现对转子的驱动.定子线圈通电25 A,其磁场模值分布如图8所示,定子线圈在转子球产生的最大磁场0.13 T左右.综合考虑铌材料的临界磁场、转子的驱动稳定性和电流漏热[3],定子线圈允许通的电流不超过25 A.

图8 通电25 A 定子线圈产生磁场模值分布图Fig.8.Magnetic flux density generated by stator coils energized 25 A.

定子线圈通电10 A,转子绕其竖直轴转过360°,其驱动力矩的大小如图9,定子线圈与转子切削面正对的位置设为起始位置0°.转子在0°—22.5°,45°—67.5°,90°—112.5°,135°—157.5°,180°—202.5°,225°—247.5°,270°—292.5°,315°—337.5°力矩方向为负,作用效果使转子顺时针加速;在22.5°—45°,67.5°—90°,112.5°—135°,157.5°—180°,202.5°—225°,247.5°—270°,292.5°—315°,337.5°—360°力矩方向为正,使转子逆时针加速.光纤检测系统检测转子的旋转角度,通过逻辑电路在对应的角区间控制定子线圈电流的通断即可对超导转子始终施加同一方向的力矩,实现对超导转子的加减速.

图9 通电10 A 转子驱动力矩分布Fig.9.Distribution of torque to rotor generated by stator coil energized 10 A.

3.2 超导转子的定中转矩分析

超导转子由静止状态实现加转,必须在起转及加转过程保证超导转子的旋转主轴处于竖直状态,即“定中”,这样才能保证超导转子旋转主轴与驱动力矩的方向一致[19],实现超导转子的稳定高效的驱动.在定子线圈通电的情况下,超导球在沿任意赤道轴偏转,均受到一个回复力矩.图10 是超导转子沿任意赤道轴偏转示意图,设超导转子切削面与定子线圈正对的位置是起始位置0°,任意赤道轴与零位置的夹角为θ.由驱动结构的对称性,超导转子沿θ=0°到θ=90°区间的赤道轴旋转的受到的定中力矩,可以表征超导转子沿任意赤道轴旋转受到的定中力矩.如图11 是定子线圈通电10 A,超导转子沿任意赤道轴旋转0°到10°的定中力矩效果图,θ=45°定中力矩最大,在θ=22.5°和θ=67.5°定中力矩最小.

图10 超导转子赤道平面示意图Fig.10.Diagram of the superconducting rotor equatorial plane.

图11 超导转子绕任意赤道轴定中力矩分布图Fig.11.Distribution diagram of the torque to make superconducting rotor erect.

超导转子驱动时,超导转子的的定中性能主要由定中力矩、质量偏心和超导转子的转速决定.其中加转前的定中性能直接决定超导转子的“起转”能否顺利进行,起转后的定中性能影响超导转子的驱动力矩.首先分析加转前的定中性能,超导转子的质量偏心有两种情况,如图12,其中O是转子形心,C是转子质心,OZ是转子极轴,OK是竖直方向,α0是质量偏心转子球心连线与转子极轴的夹角,α 是转子极轴与竖直方向的夹角.

图12 超导转子的两种类型质量偏心图Fig.12.Two types of mass eccentricity model diagram for superconducting rotor.

首先分析转子质量偏心在上半球,如图12(a),则动力学方程:

式中,m是转子质量,g是重力加速度,l是质量偏心量,T定中力矩,Je是赤道轴转动惯量.

当α0=0°,α|t=0=0°时,由结构对称性得出,定子绕组对超导转子的定中力矩T=0,则由方程(2)得出超导转子始终保持在竖直状态;当α0与α 不同时为0,则超导转子在竖直方向无法保持稳定,此时求解方程(2),可得出超导转子的定中特性.由图11 知,超导转子定中效果在θ=45°最好,在θ=22.5°定中效果最差,下面主要分析超导转子绕这两位置的赤道轴偏转时,超导转子的定中效果,以此评价整个系统的定中效果.图13 是定子线圈通电10 A,赤道轴在θ=22.5°和θ=45°角位置的定中力矩T和极偏角α 的拟合曲线.

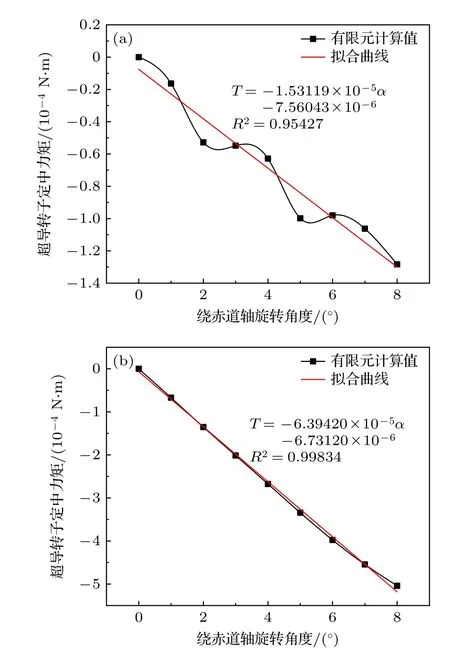
图13 超导转子的定中力矩分布 (a) θ=22.5°;(b) θ=45°Fig.13.Torque distribution to make superconducting rotor erect: (a) θ=22.5°;(b) θ=45°.

可得超导转子在绕θ=22.5°和θ=45°角位置的赤道轴旋转时,定中力矩T与极轴偏角α 有很好的线性关系:

式中,kθ和b是拟合系数.将α 取小角度对(2)式进行化简,将(3)式中的α 单位化成弧度,然后代入(2)式:

要使方程(4)有稳定解,必须使m1<0,设方程(4)的初始条件:

其中ε 是初始极轴偏角,则方程(4)的解为

根据方程(7)可以确定定子作用下,超导转子极轴的极偏范围(–2m2/m1– ε,ε),由于阻尼的存在,超导转子最终的平衡位置是–m2/m1,则可以用–m2/m1衡量超导转子的定中效果,m2/m1值越小,其定中效果越好,超导转子的轴向质量偏心通常远大于其径向质量偏心,即α0=0°,同时设ε=1°.将超导转子的参数代入方程及其约束条件,即m1<0,可以得出超导转子在绕θ=22.5°赤道轴偏转时,质量偏心l<1.067 mm,可以对超导转子进行定中;在绕θ=45°处的赤道轴偏转时,质量偏心l<4.450 mm,可以对超导转子进行定中.图14 是力矩线圈通电10 A,质量偏心l与其极轴平衡位置–m2/m1及振动范围(–2m2/m1– ε,ε)的关系图.

图14 超导转子定中 范围及平衡位置 (a) θ=22.5°;(b) θ=45°Fig.14.Centering range and balance position for superconducting rotor: (a) θ=22.5°;(b) θ=45°.

图14 表明随着质量偏心的增大,其定中效果减弱,定子线圈通电10 A,初始极偏角ε=1°时,质量偏心500 μm 的超导转子绕θ=22.5°位置的赤道轴偏转时其振动范围是(–2.86°,1°),最终在α=–0.93°的位置平衡;绕θ=45°位置的赤道轴偏转时其振动范围是(–1.24°,1°),最终在α=–0.12°的位置平衡.同理可以分析超导转子质量偏心在下半球的情况,如图12(b),此时设α0=0°,同时设ε=1°,则重力矩方向与定中力矩是同方向,超导转子是自稳定的,振动范围(–1°,1°),振动极偏角主要与其初始极偏角ε 有关.综上,在初始极偏角为1°时,定子线圈通电10 A,定中力矩最差的偏转方向也可使质量偏心500 μm 的超导转子定中在2.86°极偏角的范围内,最终在0.93°极偏角位置平衡.实际超导转子质量偏心远小于500 μm,故力矩线圈通电10 A,可以将超导转子定中在1°以内.在超导转子极轴偏角一定时,定中力矩与电流平方成正比,按照上述的分析方法,可以计算力矩线圈通其他电流时超导转子的定中效果.

如力矩线圈通电5 A,由m1<0 可以得出超导转子在绕θ=22.5°赤道轴偏转时,质量偏心l<0.267 mm,可以对超导转子定中.当超导转子的质量偏心是200 μm,初始极偏角是1°,超导转子的定中范围是(–4.96°,1°),平衡位置是α=–1.98°.通过Ansoft 仿真超导转子在极偏0°—8°的情况下,极轴偏角α 对超导转子驱动力矩的影响.如图15,极轴偏角8°以内,相同角区间对应的驱动力矩方向一致,故定子线圈的定中效果可满足控制系统的要求.

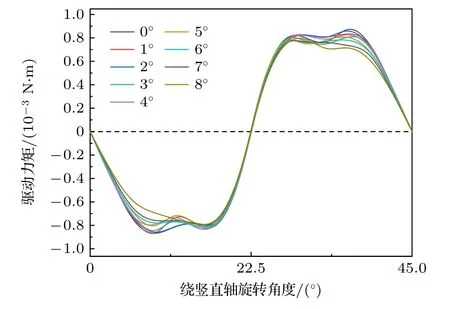
图15 超导转子在不同极偏角下的驱动力矩分布Fig.15.Driving torque distribution with different inclination angles for superconducting rotor.

4 定中和驱动一体化的超导转子驱动方法

上述分析表明定子线圈可同时满足超导转子的驱动和定中要求.基于此,本文提出了一种定中驱动一体化的超导转子驱动方法.定子线圈采用双绕,一路始终通电用来维持转子的定中效果-定中路,另一路通过逻辑电路控制通断驱动超导转子-驱动路.

4.1 超导转子驱动过程力矩分析

定子线圈单路通电1—10 A 时,其驱动力矩在一个驱动周期的力矩分布如图16.转子驱动力矩T与转子角速度w的关系为

图16 单路定子线圈通电的驱动力矩Fig.16.Driving torque of the single-circuit stator coil energized with current.

可以推出:

式中,Jz是转子的旋转主轴转动惯量,θ 是转子旋转主轴(Z轴)的转动角度.故T对θ 的积分可以反映出系统的驱动效果.在一个驱动角周期45°中,有效驱动是半个周期,对半个周期内单路定子线圈依次通电1—10 A,并对半个有效角周期积分,结果如图17.

图17 半驱动角周期力矩积分与驱动电流的关系Fig.17.Relationship between half cycle torque integration and driving current.

有效力矩T对旋转角度θ 的积分与驱动电流I的平方成正比.由此可计算设计线圈的驱动力矩,设一路线圈始终通电I1,主要用来保证转子的定中效果,一路线圈按驱动时序通电I2用来实现转子的驱动.则在一个加转周期中,驱动路和定中路同时作用是,驱动力矩对角度积分为

在定中路单独作用的半周期,力矩对角度的积分为

则转子在一个驱动角周期的总的驱动力矩积分:

所以定子线圈中定中路一直通电会增强驱动路对超导转子的驱动效果,同时驱动路通电时也会增强定中路对超导转子的定中效果,即二者是相互增强的.在实际通电过程中要保证定中路和驱动路的电流方向相同,否则二者相互消弱.当定中路和驱动路各10 A,对超导转子进行顺时针加转,其驱动力矩分布如图18.

图18 定中驱动一体化结构的驱动过程力矩分布Fig.18.Torque distribution during the driving process.

4.2 超导转子的驱动控制时序设计

通过转子顶部贴花纹,使光纤探测系统在转子旋转0°—22.5°,45°—67.5°,90°—112.5°,135°—157.5°,180°—202.5°,225°—247.5°,270°—292.5°,315°—337.5°时,输出低电平(逻辑“0”);在22.5°—45°,67.5°—90°,112.5°—135°,157.5°—180°,202.5°—225°,247.5°—270°,292.5°—315°,337.5°—360°时,输出高电平(逻辑“1”);逻辑电路输出“0”表示受控电源停止对定子线圈供电,输出“1”表示受控电源对定子线圈供电,则其逆时针转动过程的加减速逻辑时序信号如图19,顺时针转动过程的加减速逻辑时序信号如图20.

图19 逆时针旋转逻辑电路时序信号Fig.19.Counterclockwise logic circuit control.

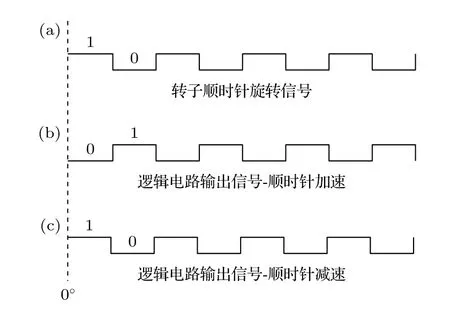
图20 顺时针旋转逻辑电路时序信号Fig.20.Clockwise logic circuit control signal.

驱动系统主要依靠光纤传感器和花纹图案对超导转子的旋转角位置进行探测,花纹图案与转子顶部的光纤传感器的相对位置如图21,两个黑色的原点表示光纤探头在花纹上的投影,探测光纤中有激光发射光纤和接收光纤.激光在花纹上发生漫反射,在转子面发生镜面反射,从而实现对转子的旋转位置检测[20].八花纹的功能是对超导转子的旋转位置进行测量,从而完成对超导转子的驱动;转速花纹对超导转子的转速进行测量;转速花纹和八花纹输出电平的相对相位关系用来判断转子的转向,如图22.

图21 转子花纹图案Fig.21.Rotor pattern.

图22 转速信号和八花纹信号的相位关系 (a) 逆时针旋转;(b) 顺时针旋转Fig.22.Phase relationship between rotational speed signal and eight pattern signal: (a) Counterclockwise;(b) clockwise.

花纹图案外围八花纹包括8 个圆心角为22.5°的无顶角扇形图案,八花纹图案都有一个边正对着赤道切削平面的中心线,另一条边正对两个相邻切削平面之间的分界线;转速花纹是一个圆心角22.5°的扇形图案,转速花纹的外缘与八花纹的内缘相切,转速花纹的一条边和与其相切的无顶角扇形图案的角平分线重合.

5 驱动结构的驱动效果评估

5.1 定子系统的响应特性分析

超导转子驱动效果主要指超导转子加转到额定转速需要的时间.为了避免超导转子失超,上述定子线圈在驱动过程的驱动路和定中路的总电流I定中+I驱动要求不超过25 A.上面已经计算出定中路通电10 A 和5 A 可以对转子定中,定中路分别通电10 A 和5 A,驱动路通电1—10 A,平均驱动力矩如图23.驱动路电流一定时,定中路电流越大,平均驱动力矩越大,即驱动效果越好.

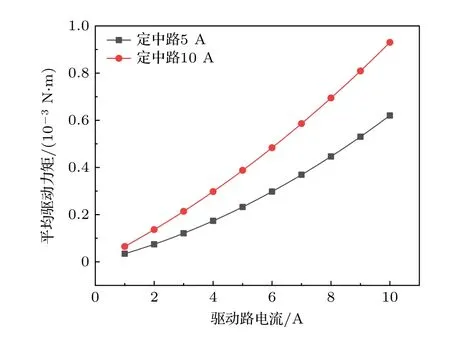
图23 定中电流10 A 和5 A 时,不同驱动电流的平均驱动力矩图Fig.23.Average drive moment of different driving currents with another circuit energized 10 A and 5 A.

接下来分析超导转子的驱动过程.定子回路通电过程可简化成一阶电路,如图24,定子回路电感主要由定子线圈电感L决定,定子回路电阻r主要由常温区到低温区的引线电阻决定.通过有限元软件可以模拟出定子线圈电感69.8 μH,定子回路电阻设为2 Ω,则可以得到超导定子线圈定中路电流的响应方程[21]:

图24 定子回路系统示意图Fig.24.Schematic diagram of stator circuit system.

式中,I0是驱动电源设置电流;I(t)定子回路在激励过程的响应.

超导转子的响应时间即定子电流上升到目标电流的时间:

则超导转子在驱动过程中,每个脉冲电流的宽度大于0.08 ms,定子线圈电流才能达到预设的目标电流.图25 中t0是驱动过程中的定子回路的脉冲宽度,随着超导转子转速的增加,脉冲宽度t0越来越小,上升时间占据的比例逐渐增大,定子输出的有效力矩越来越小.考虑定子系统响应计算超导转子的驱动时间是十分复杂的,为了简化计算本文只计算超导转子驱动到50 Hz 的驱动时间.因为超导转子转速50 Hz 对应的定子脉冲宽度1.25 ms,上升时间只占6%.此时可忽略定子电流的响应引起的输出效率变化.

图25 定子回路电流响应Fig.25.Current response of stator circuit.

5.2 驱动到50 Hz 的加速时间计算

设定中路通电5 A,驱动路通电1 A,计算顺时针加转超导转子到3000 r/min 的时间.超导转子从(n– 1)个驱动角周期,每个驱动角周期45°,到n个加转周期的起始角速度wn通过(10)式和(13)式可计算:

则可以通过(16)式计算出加转到3000 r/min 需要的加转驱动角周期数68528.通过拟合超导转子在第n个驱动角周期(45°)中的T-θ 曲线:T=f(θ),可以计算超导转子在每个角加转周期的加转时间tn:

式中,wnθ是第n个加转周期中(0°,45°)中任一角位置的角速度,wnθ表示式为

根据(16)式、(17)式和(18)式可以计算出tn,则总的加转时间t总:

由(16)—(19)式可以计算出,定中电流5 A,驱动电流1 A 时,可用342 s 将超导转子驱动到3000 r/min.同理可以计算出任意定中电流和驱动电流对应的加速时间,如图26.图26 表明,定中路的电流越大,超导转子的加转时间越短.以上驱动时间的计算结果是忽略气体阻尼及驱动电流源的输出特性的理想情况下的计算结果.所以在实际驱动过程中要考虑实际的条件,如转子的质量偏心、低温系统的传热效率、临界转速等合理设置I驱动和I定中的大小,以此来调控超导转子的驱动时间.四个盘形定子线圈也起到对超导转子侧向支撑的作用,可以在一定的范围内对超导转子的侧向支承刚度进行调控.

图26 定中电流为10 A 和5 A 时,不同驱动电流加转到50 Hz的时间Fig.26.Time for the superconducting rotor to be accelerated to 50 Hz by applying different driving currents with centering current of 10 A and 5 A.

6 结论

本文设计了一种结构简单的超导转子驱动电磁结构,其中转子结构完全对称理论质量偏心为零,并通过有限元方法研究了定子磁场对超导转子的转矩作用,定量地分析了定子对超导转子的驱动和定中效果.

针对所设计的超导转子驱动电磁结构,提出了一种基于超导体迈斯纳效应的定中-驱动一体化的超导转子驱动方法.即定子线圈双绕,一路始终通电产生转矩对超导转子定中,另一路按一定的控制时序通断电对超导转子进行驱动.设计了超导转子顶部的花纹图案和定子线圈驱动路的控制时序;分析了此驱动方法驱动过程中定子线圈定中路和驱动路对超导转子的转矩分布.

最后分析了定子系统在驱动过程的响应特性,计算了超导转子驱动到50 Hz 需要的驱动时间.结果表明,此驱动结构的加转时间由定子线圈的驱动路电流和定中路电流共同决定,两者电流方向相同时,定中电流可以增强驱动效果,驱动电流同样可以增强定中效果.本文介绍的超导转子驱动方法与已经报道出的超导转子磁浮装置驱动方法相比,此驱动方法简化了超导转子结构和驱动电磁结构,为进一步优化旋转超导转子的测角精度提供了参考.