超导动态电感探测器的噪声谱分析*

石中誉 代旭城 王浩宇 麦展彰 欧阳鹏辉 王翼卓 柴亚强 韦联福 刘旭明 潘长钊 郭伟杰† 舒诗博 王轶文‡

1) (西南交通大学物理科学与技术学院,量子光电实验室,成都 610031)

2) (南方科技大学深圳量子科学与工程研究所,深圳 518055)

3) (深圳国际量子研究院,深圳 518048)

4) (西南交通大学信息科学与技术学院,信息量子技术实验室,成都 610031)

5) (中国科学院高能物理研究所,粒子天体物理重点实验室,北京 100049)

1 引言

动态电感探测器[1](kinetic inductance detector,KID)是基于超导微波谐振电路[2]的光子探测器.当吸收光子能量大于超导能隙时,超导体内库珀对被破坏产生准粒子,引起超导薄膜表面阻抗的变化,进而带来谐振频率和谐振峰品质因数(Q)的变化,以此来进行灵敏的光子探测.超导材料具有毫电子伏特量级的能隙,因此探测光谱较宽,覆盖了从(亚)毫米波、可见/近红外到X 射线波段.KID 具有容易频域集成的突出优势[3],以及本征的光子能量/数目分辨能力[4–6],目前已经应用于(亚)毫米波和光学波段的阵列探测中[7–10].

在单像素性能层面,KID 的噪声水平为关键指标之一.自KID 在2003 年被发明以来[1],人们对其损耗及噪声行为进行了大量研究,发现电介质中的二能级系统(two-level system,TLS)[11]有重要影响.TLS 的电偶极矩可与谐振器内部电场耦合,带来介电常数的涨落从而引起频率噪声(即谐振频率的涨落)[12].对于最常见的共面波导[13]和集总电路这两种平面结构的超导谐振器,研究表明谐振电路薄膜与衬底界面处的TLS 对损耗和噪声的贡献占主导[14].通过优化工艺手段[15–17]和器件设计[18,19],KID 的灵敏度近年来快速提升,目前已经在多种超导材料(包括TiN,Al 和NbTiN/Al)和电路结构(共面波导及集总电路)的KID 中,采用频率或幅度读取,实现了受背景光子噪声限制的探测灵敏度[20–24].

准确且高效地对动态电感探测器的噪声谱进行分析非常重要,但尚没有文献对此做仔细探讨.因此,本文首先详细介绍了一种适用于KID 的噪声采集和噪声谱分析方法,通过在不同频率区间设置不同的分辨率,较好地平衡了噪声频谱分辨率与方差性能.其次,将这种方法应用于两组工艺制备的超导铝(Al)动态电感探测器的噪声表征中,发现在Al 膜上下加氮化硅( SiNx)介质层可以有效地降低暗噪声水平: 在同一谐振器内部功率下,双层 SiNx工艺器件的频率噪声约为裸铝器件的25%—50%.最后,系统研究了基于双层 SiNx工艺的集总结构Al KID 的频率噪声行为.我们设计和制备了几组不同电容和电感尺寸的器件,在不同微波驱动功率和温度下测量了它们的噪声特性,实验结果表明电容区的 TLS 噪声占主导.

2 噪声数据采集

实验测量线路采用零差探测方案,如图1(a)所示: 微波源产生的微波信号通过功率分配器分为两路,一路直接接到混频器(Polyphase AD0540B,幅度不平衡度约±0.05 dB)的本振端口(LO),另一路经过可调微波衰减器接入低温微波电路,经过待测的KID 样品后,通过低温微波放大器(LNFLNC03_14A)和常温微波放大器(MINI ZVA-183X-S+)放大,接到混频器的射频端口(RF).两路微波信号经混频器解调后输出为I(in-phase)和Q(quadrature)两路信号,经过低通滤波器(DC-1 MHz)后由数字采集卡(A/D 卡,NI PCI-6133)转化为数字信号,经过数字滤波(通带边界频率2kHz,阻带截止频率 5 kHz)处理后存储.

图1 (a)实验测量线路示意图;(b)复平面上的谐振圆及噪声示意. Zc 是谐振圆的圆心,Zr 是谐振点.红色的点代表谐振点随时间的飘移( δZ(t)),可正交分解为切向的频率分量和法向的幅度分量Fig.1.(a) Schematic diagram of the measurement circuit;(b) schematics of the resonance circle in complex plane and noise. Zc is the center of the resonance circle and Zr is the resonance point.The red points represent the resonance frequency shift with time( δZ(t)),which can be projected into frequency and amplitude components,with directions tangent and normal to the resonance circle respectively.

在数据采集时,首先在谐振频率附近扫描驱动微波信号的频率f,以测量稳态时的微波传输曲线(S21),得到复平面(Z-平面,Z=S21)上的谐振圆(见图1(b)).通过寻找|dZ/df|的最大值,得到谐振点Zr和谐振频率fr.然后将微波信号的频率固定在fr,进行时域上噪声数据的采集,t时刻的数据点为Z(t) ,其与谐振点均值的偏离量δZ(t)=Z(t)-Zr表示噪声.通过计算:

可将噪声正交分解为切向(平行于 (∂Z/∂f)Zr方向)的频率噪声分量x(t) 和法向(垂直于(∂Z/∂f)Zr方向)的幅度噪声分量y(t) ,其中 (∂Z/∂f)Zr为谐振点处S21随频率的变化率.进一步推导[2]可得到x(t)=δfr(t)/fr为分数谐振频率的涨落,即频率噪声;y(t)=δ(2Qi(t))-1(Qi为内部品质因数),代表谐振圆半径的涨落,即幅度噪声.

实验中以Fs=2.5 MHz 的采样频率进行T=100 s 时域数据的连续采集.根据Nyquist 定理,噪声谱分析的最高频率为Fs/2=1.25 MHz.而理论上的最小分辨率为 1/T=0.01 Hz,但实际操作中选择 0.1 Hz 为最小分辨率以保证结果具有较小的方差.由于低频噪声在较长的时间才能体现,为去除冗余数据和提高效率,以 2 kHz 为界将噪声频谱分为低频段和高频段两部分.对于低频段(0.1 Hz—2 kHz),采用降采样的处理方法,抽取比例为250∶1,因此等效的采样频率为 10 kHz ,100 s共采集 106个数据点.同时为防止频谱混叠须在抽取时添加FIR 数字低通滤波器[25],其通带边界频率设为 2 kHz .对于高频段(2 kHz—1.25 MHz),采用最后1 s 的连续数据,共 2.5×106个数据点用于噪声分析.

3 噪声功率谱分析方法

本文基于Welch 法[26]进行噪声功率谱估计,Welch 法是对经典周期图法(即Bartlett 法)[27]的改进,体现在允许数据分段有交叠以减小谱方差,以及每段数据可以加窗函数以减少频谱泄露.但传统Welch 法只设置一个频率分辨率( ∆f),对于宽频的噪声谱分析,可能会导致谱分辨率和方差不能很好地平衡,因此本文在处理数据时对不同频率区间设定了不同的分辨率,主要参数见表1.

表1 噪声谱分析参数Table 1. Noise spectrum analysis parameters.

图2 给出了噪声谱分析的主要流程.假设所有噪声数据是长度为N的序列x[n](n=1,2,···,N),分辨率 ∆f决定了数据的分段长度M=Fs/∆f,设相邻两段数据的重叠点数为D(重叠率为D/M),则噪声数据的分段数为将第i段(i=1,2,···,L)数据序列表示为xi(n)=x[(i-1)×(M-D)+n+1](n=0,1,···,M-1),由Parseval定理可计算第i段数据的功率谱为

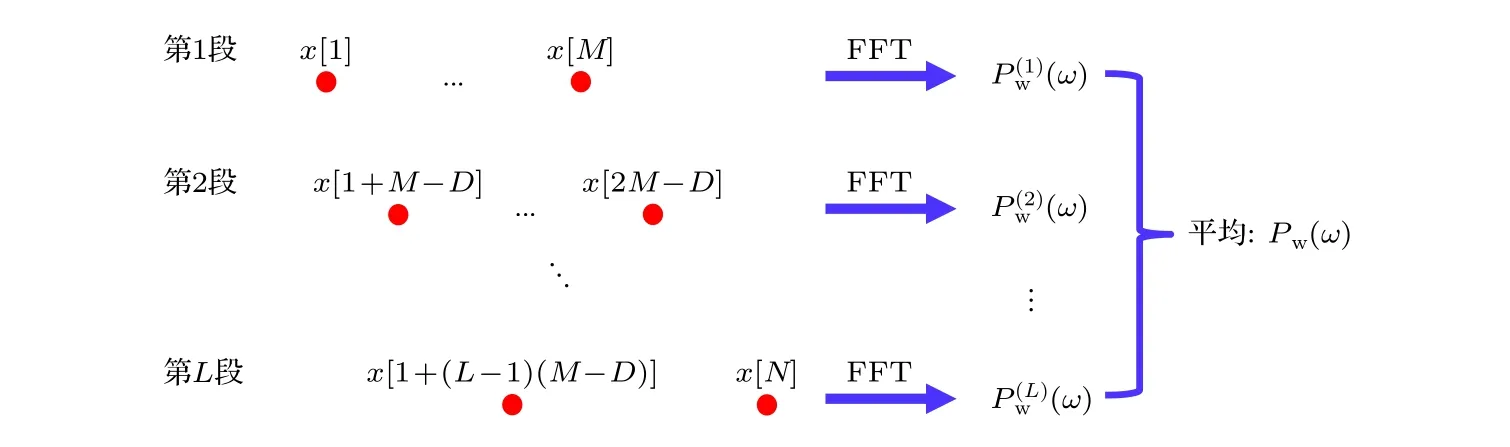
图2 数据处理示意图.噪声数据被分成L 段,每段数据长度为M,相邻两段数据的重叠点数为DFig.2.Schematic diagram of data processing.The data is grouped into L segments,each segment contains M data points and D overlapped points with adjacent segments.

按照表1 中的参数,对每个频率区间都做如上计算,就得到了 0.1 Hz— 1.25 MHz 的频率噪声谱和幅度噪声谱.

图3(a)给出了一个典型的KID 噪声功率谱,数据来自图4(b)中一个标准尺寸设计的集总谐振器样品(结构2)在微波功率Pint=-52.5 dBm 下测得的噪声.该噪声谱有两个主要特征: 首先,在较低频段( <200 Hz)的频率噪声相比幅度噪声高了约两个量级,后面会说明这种过量的频率噪声有很强的微波功率依赖关系,具有二能级系统噪声的典型特征;其次,幅度噪声谱除了在小于 10 Hz 的频段有类似 1/f噪声的上翘之外,在整个频段是很平的,噪声平台与线路中使用的噪声温度Tn≈4.2 K的低温微波放大器一致.此外,频率噪声在约500 Hz处开始明显下降,该滚降(roll-off)频率由谐振器带宽(fr/2Q)和频率噪声本身的带宽共同决定.图3(a)中,采用 100 s 数据降采样得到的低频段的频率噪声谱(红线)画到了 5 kHz,而采用最后1 s连续数据得到的高频段的频率噪声谱(蓝线)则从2kHz 开始.在接近 5 kHz 的区域,红线整体低于蓝线,这是因为在降采样时使用的数字低通滤波器在超过通带边界(2 kHz)时起了作用.而在 2 kHz处,两段噪声谱几乎重合,这保证了噪声谱在分界处的连续性,也说明了本文算法的有效性.

图3 (a)一个典型的KID 噪声功率谱,其中红点和蓝点分别代表用100 s 的降采样数据和最后1 s 的连续数据计算得到的2 kHz 处的频率噪声;(b) 频率分辨率对噪声谱的影响Fig.3.(a) A typical noise spectrum for a KID.The red dot and blue dot represent the calculated frequency noise at 2 kHz from the decimated 100 s data and the last 1 s continuous data,respectively.(b) Effects of frequency resolution on noise spectrum.

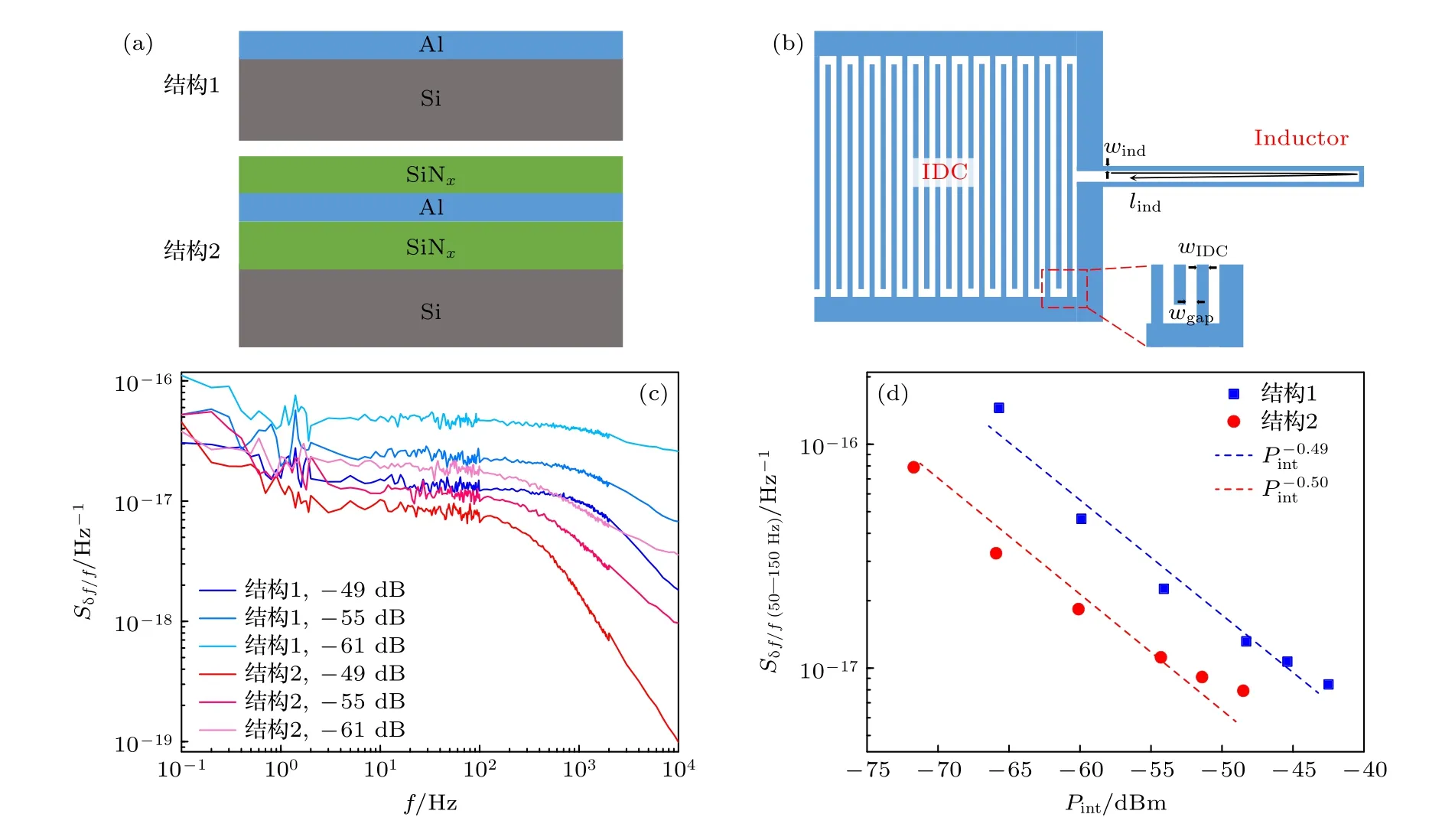
图4 (a)两种不同的谐振器工艺结构示意图;(b)集总电路谐振器几何设计示意图;(c)两种谐振器在不同微波功率(谐振器内部功率)下的频率噪声谱;(d) 50—150 Hz 的频率噪声随谐振器内部功率的变化,可以看到双层 SiNx 结构的谐振器在相同功率下具有更低的噪声Fig.4.(a) Schematics of two different fabrication structures for resonators;(b) geometrical design of the lumped-element resonator;(c) the measured frequency noise spectrum of two resonators with different fabrication structures at various microwave powers (the internal power of resonator);(d) the frequency noise at 50–150 Hz with resonator internal power,showing the resonator with double SiNx layers has a lower noise level at the same internal resonator power.

图3(b)给出了不同分辨率下的噪声谱估计.以 3—10 Hz 区间的幅度噪声为例,在 50 和 60 Hz 处有两个特征噪声谱峰.分别采用 0.1,1 和 10 Hz 三种分辨率对噪声功率谱进行估计,发现 0.1 Hz 分辨率的噪声谱的分辨能力最好但背景起伏(方差)太大,10 Hz分辨率的噪声谱方差很小但分辨不出两个特征谱峰,而 1 Hz 分辨率的噪声谱既能分辨谱峰又有比较平滑的背景起伏.通常,在较低频段更注重谱的分辨率,在较高频段则更注重谱的方差性能,因此本文采用表1 中的分辨率设置,以较好地平衡分辨率与谱方差性能.对于数据分段时的重叠率,分别研究了10%,50%和90%三种重叠率下的噪声功率谱,发现谱的方差随重叠率增加而减小,但高重叠率会增长运算时间,因此我们最终选择了50%的重叠率.

4 Al KID 的噪声谱研究

铝(Al)作为常规超导体,因为其易加工性,是制备超导谐振器最常见的材料.我们也正在研制应用于亚毫米波段的光子噪声极限以及应用于光学波段的光子能量和数目可分辨的超导Al 动态电感探测器.为了理解Al KID 的噪声特性,本文探究了两种基于薄铝的工艺结构,如图4(a)所示: 结构 1 为裸铝器件,即在高阻硅(Si)衬底上直接镀25 nm 厚的Al 膜,光刻形成电路;结构 2 为双层SiNx结构,即在高阻硅(Si)衬底上先镀20 nm厚的 SiNx介质层,再制备25 nm 厚Al 膜电路,顶层再镀 50 nm 厚 SiNx保护层以防止Al 的氧化.为了提高器件的响应度,Al 膜需要做薄,但Al 膜太薄会降低器件的品质因数和准粒子产生效率[28,29],因此本文制备的Al 膜的厚度设定为 25 nm .

本工作制备的器件均在〈100〉晶向高阻硅上生长,硅片电阻率大于10000 Ω· cm.在样品生长前硅片先在丙酮和异丙醇中进行超声波清洗,然后在食人鱼溶液(浓硫酸和过氧化氢的混合物)中浸泡以清除有机残留物,最后用氢氟酸清洗去除硅片表面的氧化层.硅片清洗后,对于裸铝样品,直接在衬底表面进行涂胶/光刻/显影,并用等离子体去胶;再送入电子束蒸发设备,在真空度5×10-9Torr(1 Torr≈133.322 Pa)的环境中完成铝膜生长,铝膜沉积速度 0.5 nm/s ,沉积厚度 25 nm ;最后利用剥离工艺完成器件制备.对于双层 SiNx结构的样品,铝膜电路的工艺与裸铝样品完全一致.而 SiNx介质层则使用等离子体增强化学气相沉积设备(PECVD)在低温(80 ℃)条件下生长.采用低温生长是考虑到在做顶层 SiNx时,如果温度较高,可能使得下层的铝膜在高温下发生质变,因此本工作中的两层 SiNx沉积均采用了低温工艺.

图4(b)给出了本工作中一个标准的集总式谐振器的几何设计,即一个交指电容(IDC)与一根细长的电感窄条并联.其中IDC 的面积较大,约为1 mm×1 mm,手指的宽度和间隔相等wIDC=wgap=4 μm,电感条的宽度wind=2 μm,电感条长度lind=3 mm .对于 25 nm 厚的Al 膜,其动态电感约为0.6 pH/square,这样的设计对应约1 GHz的谐振频率.谐振器通过电容与一条微带线馈线耦合,其耦合品质因数设计为Qc≈20×103.采用图4(a)中的两种工艺制备了上述设计的谐振器,并使用矢量网络分析仪(VNA)测量了器件低温时(约 50 mK)的微波传输曲线,主要结果见表2.可以看到两个谐振器具有接近的谐振频率,主要区别在于结构 1 的谐振器相比结构 2 具有更高的内部品质因数(Qi)和更高的非线性功率(Pbif),具体原因有待进一步研究.

表2 两种工艺结构的谐振器测量参数Table 2. Measured parameters of resonators with two fabrication structures.

本文对两种谐振器在不同微波驱动功率下进行了频率噪声的测量与分析,所使用的最大微波功率比器件的非线性功率Pbif低约 2 dB .为了方便比较不同品质因数的谐振器的噪声水平,本文中的微波功率统一为谐振器内部的功率Pint,其与馈线上的读出功率Pread的关系为可通过微波源的输出功率及线路上的衰减估计得到.图4(c)给出了两个谐振器在 3 个微波功率下的频率噪声谱,可以看到噪声随着微波功率的升高而降低,其中谐振器1 的噪声总体上在谐振器2 的噪声上方,除了低频处(<1 Hz)的噪声交织在一起.此外,谐振器1 相比谐振器2 具有更高的滚降频率.为了更清楚地比较两个谐振器的噪声水平,将滚降频率之前的 50—150 Hz 处的频率噪声取平均,对谐振器内部功率作双对数图,得到图4(d).可以看到,在相同的Pint处,谐振器2 的频率噪声是谐振器1 的25%—50%,即采用双层 SiNx工艺的谐振器具有更低的噪声.该噪声水平与共面波导结构的40nm 厚Al 谐振器的噪声水平大致相当[19].对两个谐振器,频率噪声对Pint的双对数图都可以用斜率约 -0.5 的直线拟 合,说明频率噪声与正比,这是二能级系统噪声的典型特征[11].相同情况下,双层 SiNx结构的样品比裸铝样品具有更低的噪声,我们认为可能是下层 SiNx能避免Al 膜与Si 衬底表面自然形成的 SiO2氧化层直接接触,而SiO2层通常被认为会带来较大的TLS 噪声[30].后续我们将进行更多实验以明确双层 SiNx结构可以降低TLS 噪声的原因.

为了进一步研究双层 SiNx工艺的Al KID 的噪声特性,制备和测试了不同电感条宽度/长度,以及不同IDC 宽度/间隙的集总式谐振器,噪声测量的主要结果总结在图5 中.其中,图5(a)给出了不同电感条宽度(电感条长度lind=3 mm 不变)的样品噪声随内部功率的变化: 可以看到宽度越窄,谐振器的非线性功率越低,噪声水平越高,但大致都落在了一条斜率为 -0.5 的直线上.图5(b)给出了不同电感条长度(电感条宽度wind=2 μm 不变)的样品噪声随内部功率的变化: 可以看到非线性功率随长度变化不大,因为其主要取决于电感条宽度[31],所有数据也都大致落在了一条斜率为-0.5的直线上.图5(c)中,改变IDC 的宽度及间隙,而保持电感条的宽度和长度不变(lind=3 mm,wind=2μm).对于这组样品,因为电感区是相同的,所以非线性功率大致相同.而IDC 宽度/间隙越宽的样品,噪声水平越低,这与前期的研究结果[32]一致,因为IDC 的宽度/间隙越大,填充因子越小,电容区TLS 噪声带来的影响也就越小.但宽度越宽,谐振器电容的面积就越大,不利于节约KID 像素的尺寸.拟合得到的噪声随功率变化的斜率在-0.35 到 -0.55 之间,与-0.5 有较大偏离,可能是制备该组样品时具体工艺参数变化带来的影响导致的.最后,图5(d)中,对标准设计的谐振器做了变温实验,在不同温度下测量了谐振频率的移动和噪声水平.发现噪声随着温度的升高先下降,在150—200mK 附近达到最低点后,再迅速上升.而谐振频率随着温度升高先缓慢上升,同样在150—200mK 附近达到最大值,然后迅速下降.谐振频率的移动 ∆fr/fr可以用一个基于BCS 理论和TLS 损耗理论的模型[12]很好地拟合:

图5 (a)不同电感条宽度谐振器的频率噪声;(b)不同电感条长度谐振器的频率噪声;(c)不同IDC 手指和间隙宽度的谐振器的频率噪声;(d)谐振频率及频率噪声随温度的变化Fig.5.(a) Frequency noise of resonators with different inductor widths;(b) frequency noise of resonators with different inductor lengths;(c) frequency noise of resonators with different IDC finger and gap widths;(d) resonance frequency shift and frequency noise versus bath temperature.

5 结论

本文详细介绍了一种适用于超导动态电感探测器的噪声测量和噪声谱分析方法,通过在不同频段设置不同的分辨率,可以较好地平衡噪声频谱分辨率与方差性能,准确而高效地进行宽频段的噪声谱分析.利用这种方法对比了两种工艺制备的超导铝动态电感探测器的噪声水平,发现在铝膜上下两层镀氮化硅膜的样品的频率噪声约为裸铝样品的25%—50%,说明双层氮化硅结构可以一定程度地降低噪声.基于这种双层氮化硅工艺,本文系统研究了多种设计的集总电路铝动态电感探测器在不同微波功率和温度下的噪声特性,实验结果表明来自电容区域的二能级系统噪声占主导.本文提出的噪声谱分析方法可作为一种通用的方法应用于动态电感探测器的噪声表征,对双层氮化硅结构器件噪声特性的研究也为研制低噪声的超导铝动态电感探测器奠定了基础.