浅海粗糙海底声散射建模及声场特性*

汪磊 黄益旺† 郭霖 任超

1) (哈尔滨工程大学,水声技术全国重点实验室,哈尔滨 150001)

2) (海洋信息获取与安全工信部重点实验室(哈尔滨工程大学),工业和信息化部,哈尔滨 150001)

3) (哈尔滨工程大学水声工程学院,哈尔滨 150001)

4) (中国科学院声学研究所东海研究站,上海 201815)

1 引言

海洋中的声传播起伏始终是海洋声学的热点话题.海水介质的随机不均匀性、随机起伏海面及海面表层的气泡层、不平整海底及海底介质内部的不均匀性,这些都对声波产生无规则散射,造成海洋声场随机起伏[1].在浅海中,海底作为海洋波导的重要边界,其声散射特性对海洋中的声传播具有重要影响,改变了声场的空间结构和统计特性.海底的声散射又是一个非常复杂的过程,而水听器基阵的空间增益与干扰场的空间相关特性密切联系,所以开展海底散射声场建模研究具有重要理论意义.并且,海底混响是浅海混响的重要组成部分,是主动声呐的干扰,而海底声散射是混响背景干扰的主要来源.考虑不平整海底的声散射,分析海底声散射引起的声传播起伏,对工作于浅海中的主动声呐设计及性能提升具有重要理论意义.其次,海底声散射与浅海海洋声场预报、匹配场处理、海底地声参数反演等密切联系,因此其研究还具有工程参考价值.

鉴于海底声散射的重要性,早在20 世纪50 年代,Urick 就开始了海底声散射特性的测量和研究[2,3].70 年代末,Barry 等[4]研制出一种拖曳式海底反向声散射测量装置,之后Jackson 等[5]使用该设备分别对粉砂、砂质和砾石海底进行了反向声散射测量.在20 世纪70—80 年代,海底声散射测量技术快速发展,出现了多种成套的专门用于海底声散射测量的专业设备,测量精度得到了极大的提高.90年代中,Greaves 和Stephen[6]利用垂直线阵声源和水平接收阵在大西洋中脊进行了海底声散射测量.在90 年代和21 世纪初,Tang 等[7,8]进行了专门的海底声散射实验,国际也上开展了两个综合的海洋声学实验,分别为SAX99 和SAX04[9,10],其中包括对海底声散射特性的测量与研究[11–13].进入21 世纪以来,海底声散射测量及相关技术研发受到很多国家的广泛重视.Pecknold 等[14]观测了加拿大盆地的海底散射现象,Yu 等[15]测量了中国南黄海宽带砂底的反向散射特征.另外,由于中低频声呐在水声通信、水下探测等方面的广泛应用,研究者们将研究重点转向了10 kHz 以下的海底声散射的测量和研究[12,16–18].

实际散射测量实验所获得大量数据为相应的海底散射模型的建立提供了基础.Lambert 定律[19]是广泛应用的粗糙界面散射模型,它能很好地描述粗糙面上的反向散射强度,以及在相对光滑界面上较小掠射角情况下的反向散射强度与掠射角的关系[20].但Lambert 定律是半经验公式,缺乏具体的物理含义,而且仅仅描述了散射强度与掠射角的关系,与海底粗糙度参数无关.因此Ellis 和Crowe[21]、Caruthers 和Novarini[22]对Lambert 定律进行了改进,给出一种与其类似的三维散射强度计算模型.侯倩男和吴金荣[23]基于海底对声散射的物理机理也建立不同于经验散射模型的物理散射模型.Kirchhoff 近似模型适合粗糙界面起伏变化比较缓慢的情况,Jackson 等[24]将此模型用于计算镜反射方向附近频率为10—100 kHz 的海底声散射,并将散射测量数据与Kirchhoff 模型预测进行了对比.不过Kirchhoff 近似模型未考虑影区效应和多次散射,现在主要用于计算缓变粗糙海底条件下垂直方向附近的海底散射声场.小粗糙度微扰近似模型适用于粗糙界面起伏很小(小于入射波波长)且界面斜率足够小的情况.Kuo[25]给出了无损耗流体沉积物情况下的小粗糙度微扰近似流体模型的表达式,Kuperman 等[26–28]也建立了各向同性小粗糙度微扰近似弹性模型,用于弹性海底声散射研究.除此之外,小斜率近似模型虽然最早是为研究海面声散射而建立的,但后来却被广泛应用于海底声散射研究[29–33].普遍认为小斜率近似比小粗糙度微扰近似和Kirchhoff 近似更为精确,而且这种近似方法几乎可以涵盖几乎所有的掠射角范围(Kirchhoff近似适合镜反射方向附近的散射,小粗糙度微扰近似适合镜反射附近之外的散射),所以就目前而言,小斜率近似是一种应用广泛的海底界面粗糙散射模型.

本文旨在建立一种水平分层介质波导中粗糙海底散射声场模型,以此分析声场特性.该模型基于简正波理论,并使用了几个基本假设.由于简正波理论的广泛适用性,模型实际上可用于大多数浅海波导环境下.本文首先推导了海底散射声场声压的简正波表示形式,再通过声压得到了海底散射声场的强度及空间相关系数的表达式;其次,利用数值方法分析了恒定声速介质中的声场特性;最后,讨论了该模型的仿真结果并给出了相关结论.

所使用的日降水量数据来源于2001—2016年临安国家基本站观测数据,以20时为日界,日降水量≥50 mm为一个暴雨雨日。本文中的季节划分方式如下:春季为3—5月,夏季为6—8月,秋季为9—11月,冬季为12月—次年2月。

2 散射声场建模

假设在中心频率f0下,声源辐射连续波,那么在同一时刻整个海底界面都对某点的散射声场具有贡献.对于一个水平环境参数不变的海洋波导,设其水层深度为zsur≤z≤zb,建立柱坐标系(r,z,φ),考虑与方位角φ无关的轴对称问题,则介质密度与声速表示为ρ(r,z) 和c(r,z) (此时的密度、声速仅是深度坐标的函数).

关于波导边界则认为波导的上方海面zsur为自由边界,并且非常光滑没有随机散射发生,而且数据表明海底散射强度值通常远高于海面散射强度值[34],所以不考虑海面散射这一假设是相对合理的.下方海底zb表现为多尺度的小粗糙度,可用h(r,φ) 表示.h(r,φ) 为随机过程,其空间相关半径为rc;另一方面,假设这个随机粗糙度h(r,φ) 是均匀各向同性的,并认为其是造成底部散射的决定因素,即只考虑海底表面粗糙度引起的粗糙散射.由于是小粗糙度,所以海底界面还是可以近似认为是平整的,这样就可以忽略传播过程中简正波相互耦合的情况.

由于整个海底都作为散射区域,则必然存在相对于发射或接收系统是近场区域的地方,但为了计算全界面散射,现将散射区域均近似认为处在发射或接收系统的远场区域.另外特别假设传播过程中海底散射只发生一次,每一个发生散射的区域足够小,以便忽略该区域内声波的衰减变化;同时,考虑的整体散射面积又必须足够大,以便研究底部散射的统计特性.

Grigor’ev 等[35]利用简正波理论建立了浅海远程海底混响模型,而且数值模拟结果与巴伦支海浅水域海底低频声散射的实验数据吻合较好.受此启发,现在尝试利用简正波表示出海底散射声场.

假设单位强度点声源的深度为zs,忽略传播过程中的频散,则距离声源水平距离为r、位于海底zb处声场的复幅度可表示为简正波之和:

式中入射的第m阶简正波为

其 中ψm为本征函数,ξm为水平波数即本征值(ξm=am+ibm),M为正常传播的简正波阶数.

考虑接收点到声源的水平距离为rn,深度为zr,假设海底散射区域表现出具有某些指向性的局部不均匀性,而且在经过r处海底散射之后,波导中正常传播的简正波的模态数目并不会发生改变,那么这种不均匀性的散射的场在接收点同样具有以下形式:

（155）盔瓣耳叶苔 Frullania muscicola Steph.刘胜祥等（1999）；马俊改（2006）；范苗等（2017）

式中r′表示海底散射区域距离接收点的水平距离,可由余弦公式求得

散射声场的第µ阶简正波为[36]

可怜的家伙，过去的几个月，他领着星雨和李离加入正意部，格物致知，诚心正意，一门心思修功夫，本来是想将由万花因隧道里碰巧得来的花间游内功尽快练到传说中的第七重，没想到，三、四、五、六，他与李离都进境神速，可达到第六重之后，却是不进反退，像一条卡在溪流中的小船，东方谷主与宇晴师父告诉两人心法与口诀，好像再也派不上用场。

Substihoting Equation(4) into Equation(1) to obtain the line velocity in the following

其中ϕ表示以声源为顶点,由散射区域中心、声源和接收点三者所形成的夹角;另外bµ(r,zb) 是散射声场中第µ阶简正波的激发系数,表示为

收集2012年1月～2014年12月收治的28例行全量放疗后、实施筋膜外全子宫切除术宫颈腺癌患者，患者病理诊断明确，随诊资料完善，年龄31～70岁，中位年龄45岁;宫颈腺癌普通型23例、绒毛腺管状癌1例、透明细胞癌1例、黏液腺癌2例和神经内分泌癌1例;高、中、低分化癌的病例依次是8例、14例和6例，临床分期(FIGO－2009年分期标准)ⅠB2期7例、ⅡA期1例、ⅡB期13例、ⅢB期7例。并取同期由于其他良性疾病行全子宫及双附件切除术患者28例为对照(对照组)。

这里ζm(r) 是一个随机过程,描述了转换为二次声源时所附加的随机起伏量;F(θµ,θm) 为表征散射声场角度重新分配的确定性函数; dS表示发生散射粗糙面元;θm和θµ分别为入射声场的第m阶简正波和散射声场的第µ阶简正波对应的声线掠射角,则有 cosθm=ξmc(zb)/(2πf0) ,θµ也同理.

根据底部粗糙度均匀各向同性的假设,随机量ζm(r)也是均匀且各向同性的,因为其独立表征了声波在不同底部区域的散射,所以它可以表示为

定值前未覆膜的先用15%噁霉灵水剂800～1 000倍液浇灌移栽苗，并及时浇透水，待地稍干整垄覆膜，以保墒、保温。

其中χm,φm分别为随机幅度与随机相位,假设它们之间是统计独立的,φm在 [0,2π] 内均匀分布,χm均服从参数为σ的瑞利分布,其概率密度函数为

综上所述，对于球状MoS2在制备耐磨复合材料的时候，其分散性能对复合材料摩擦性能的影响较大，因此需要对其粒径或表面进行进一步优化，以期使得球状MoS2的优异润滑性能得到最大程度的发挥。

其中Tm(r,zb) 为模态转换系数,表示为

浅海水域的海底散射强度对掠射角的依赖关系有着很大的变化[37],这种变化由底部散射体的波长和沉积物的物理性质决定.经过考虑,采用各向同性的Lambert 散射模型,将其用于(7)式中,那么角度分布关系可由以下表达式给出[19]:

经过分解后,接收点处的散射声压是由诸多小区块的散射声压的叠加组成,使用(6)式—(10)式,则可以将第α环上第γ块散射的激发系数表示为

NE向断裂组：这组断裂在区内最为发育，带内主要发育角砾岩或糜棱岩，该组断裂被后期断裂带切穿，构成网格状，带内具有硅化、碳酸盐化及弱钾化，平面上呈舒缓波状，产状倾向60°～90°，倾角30°～60°。

然后根据(3)式和(4)式,接收点处散射声场的复振幅有

散射声场强度:

3 散射声场特性

因此,(12)式明确描述了海底表面不平整性形成的散射声场,由其易得散射声场声压,采用Monte Carlo 方法还可以获得散射声场声压的振幅与相位的统计分布、散射声场强度和空间相关系数.随着感兴趣散射场水平位置远离声源,对该声场有贡献的海底散射区域随之增大,Monte Carlo实验的计算量也将进一步增大.

式中,角括号代表统计平均,上角标∗表示共轭,ρr和cr代表接收点处介质的密度与声速.由于空间不同海底散射体的声散射互不关联,因此其散射声场可视为不相关,将(12)式代入(13)式,统计平均体现为由于随机相位的存在,只有当下角标相等即α=β,γ=η,m=n时统计平均为非零值,此时经一系列繁琐的数学整理后有

可见,应用(14)式计算散射声场强度时,计算量得到极大降低.事实上,散射声场空间相关特性分析也可采取同样方法进行处理.

由空间相关系数公式:

对硝基苯甲脒是一种重要的化工中间体原料，在医药、染料、农药等方面有着广泛的应用，但关于它的合成少见报道。对硝基苯甲脒可以做丙烷脒药物中间体，用于防治灰霉病病菌[1-2]。国内杨凌农药化工有限公司与美国NZYM公司合作开发出了2%丙烷脒水剂，其化学名称为1,3-二(4-脒基苯氧基)丙烷。丙烷脒对灰霉病病菌防效高，用量低，单位面积的有效成分投入量小，对环境的化学污染程度低，是一种具有较好开发前景的杀菌剂[3]。目前丙烷脒的合成主要采用Pinner法进行脒基化反应，相应的反应方程式如下：

对于海底全界面的散射问题,从海底混响建模的方法出发[35],将整个海底界面以声源为圆心,以相关半径rc的宽度分解为许多小圆环,圆环的个数趋于无穷,α=1,2,3,···,∞;而每个圆环也需要以相关半径的宽度分解为许多块,区块个数为Q=2π(α-1/2),γ=1,2,3,···,Q,它是由这个圆环的中心圆的周长除以相关半径得到,在实际计算可以对其四舍五入近似进行取整,则现在每一个散射区块的面积有 dS=.界面划分方式如图1 所示,划分完成后每一个区块发生散射时的角度关系如图2 所示.在图2 所示的坐标系中,θm为入射掠射角;θµ为散射掠射角;ϑ为偏转角,描述的是入射波束在水平面上的投影的延长线到散射波束在水平面投影的夹角,若仅讨论与方位角无关的简单模型,则偏转角可不考虑.各角度的取值范围为:0◦<θm≤90◦,0◦<θµ≤90◦,-180◦≤ϑ≤180◦.

在经海底散射的声场中,不仅有沿镜反射方向传播的波,还有沿其他方向传播的散射波,镜反射方向传播的波是接收声场中确定性的相干分量,而随机的散射波则为非相干分量,所以海洋声场是相干分量与非相干分量之和,表示为

第四，进一步加强“行知合一”的研究。所谓“知行合一”的研究，就是指在构建过程中如何避免行为和理念脱节问题的研究。一方面，应加强对人类命运共同体理念的研究，找到一条可以向世界正确传递人类命运共同体理念的途径且不让人产生“排中”心理。另一方面，还应加强对构建人类命运共同体的主要力量即对各国政党的研究，要加强政党角色的研究，让各国政党在推进人类命运共同体过程中形成更多共识；要加强政党责任研究，让各国政党在推进人类命运共同体过程中凝聚更多智慧；加强政党治理研究，让各国政党在推进人类命运共同体过程中分享更多经验。总之，要进一步重视世界政党的研究，这样才能达到“知行合一”的境界。

式中Pr表示相干分量,它也可以用简正波表示;Ps表示非相干分量,其统计平均值为零.当已知海底粗糙度与随机起伏量ζm(r) 的定量关系时,海洋中相干声场与散射声场相对强度变得有意义,此时还可得到海底声散射引起的海洋声场声压的统计分布、振幅与相位起伏、空间相关特性等.同样也可得海洋声场的强度和相关系数,分别为

2)礼花弹火药的特性：主要成分：高氯酸钾、六氯苯、碳酸锶、酚醛树脂、镁铝合金粉；烟花药剂点燃后，在燃烧过程中，原有的固体烯颗粒末完全反应和(或)反应生成新的固体可燃颗粒被火焰气流带出，和空气中的氧进行二次氧化反应、产生二次亮点而形成“喷波”效果。

讨论海洋声场的这些特性有便于分析散射声场对接收到的声场信号产生何种影响,实现声场预报,而且将有助于提高声纳设备的抗干扰能力.

4 数值示例

对于海底散射问题,对某一浅海海域进行仿真,可将其近似为Pekeris 波导,海面绝对软,海底视为均匀液态半空间.平均海水深度为200 m,密度取1 g/cm3,声速取1508 m/s,底部为砂质海底,密度为1.25 g/cm3,声速为1605 m/s.发射频率为300 Hz 的连续信号,对于低频段,海水介质衰减系数αw和砂质海底纵波衰减系数αb可分别由经验公式获得[38]:

式中衰减系数单位为 dB/m ,f表示声波频率,单位为 kHz ,那么可得海水介质衰减系数约为9.92×10-6dB/m,海底纵波衰减系数约为 0.02 dB/m .海底表面粗糙度相关半径rc=20 m,均方根粗糙度取1 m,随机振幅分布参数σ=1 .具体海洋环境示意图如图3 所示.声源位于海面下10 m 处,源级为200 dB;接收点位于海面下50 m 处,距离声源水平距离20 km.在此环境下,海底起伏度小于波长,通过仿真也可知波导中传播的声线掠射角较小,即满足Lambert 定律的适用条件[20].

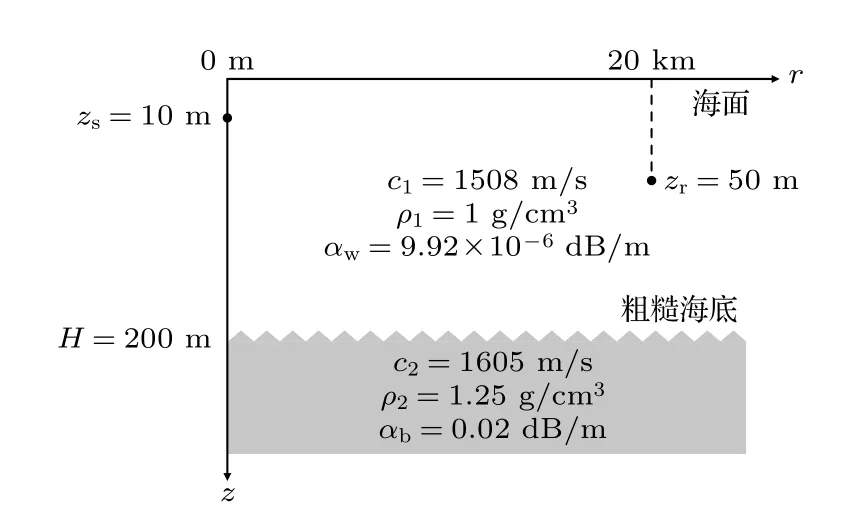
图3 海洋环境示意图Fig.3.Schematic diagram of marine environment.

为了验证推导利用统计平均所推导的散射声场强度的理论公式是否正确,先直接采用(12)式进行1000 次的Monte Carlo 实验,同时获得散射声场声压振幅与相位统计分布,如图4 所示,可见其与随机量ζm(r) 选取的分布相吻合;而后使用(14)式计算散射声场的强度,结果见图5.在考虑半径为50 km 内的海底表面散射区域时,Monte Carlo 实验的结果与理论公式所得结果几乎相同,其中微小的差值是由于Monte Carlo 方法本身造成的,这个偏差可以忽略;这两个结果对比也说明理论公式是正确的.只是对于统计平均方法,它进行的是数值计算,所以会造成误差,导致散射声场强度的结果是个复数,存在非常微小的虚部量,对此取其实部即可.而且从图5(b)可以发现,随着考虑的海底散射区域的逐渐增加,散射声场强度逐渐趋于一个稳定值,这说明对于海底声散射问题,可以根据接收点的位置确定所需要考虑的散射区域而不是整个海底,在这个区域之外发生的散射对接收点的声场的影响很微弱,可以忽略不计.所以当接收点距声源水平距离20 km 处时,可以看出此时考虑50 km 以内的散射区域就已足够.

图4 散射声场声压振幅与相位统计分布图 (a) 振幅;(b) 相位Fig.4.Statistical distribution of the sound pressure amplitude and phase of scattered sound field: (a) Amplitude;(b) phase.

图5 散射声场强度对比 (a) Monte Carlo 方法;(b) 统计处理方法Fig.5.Comparison of scattered sound field intensity: (a) Monte Carlo method;(b) statistical averaging methods.

另外,通过统计处理的方法还可以计算出不同水平距离处的散射声场强度,从而获得散射声场的传播损失特性进行散射声场预报.对于主动声纳来说,散射声场信号是背景干扰,如果接收机检测处理的是声压信号,它会造成声信号幅度与相位的随机起伏;如果是强度信号,它会造成强度增大.为了揭示散射声场的空间相关特性,计算散射声场的空间相关系数,结果如图6 所示,图中λ表示声波波长.

图6 不同海底粗糙度下散射声场空间相关系数 (a) 水平方向;(b) 垂直方向Fig.6.Spatial correlation coefficient of scattered sound field under different seafloor roughness: (a) Horizontal direction;(b) vertical direction.

在海底粗糙度小于波长的情况下,对于散射声场而言,无论是水平相关系数还是垂直相关系数都随着阵元间距增加有着周期性振荡衰减的变化规律,且后者振荡周期要更大(即空间相关半径更大),衰减也更慢,这意味着接收系统的垂直阵元间距应该大于水平阵元间距,以获得更高的阵增益.但随着海底起伏度的不断增大,海底对散射声波的传播的限制效果会越强,此时对于某点处接收到的散射声场而言有贡献的海底范围逐渐减小,散射声场开始减弱,进而造成水平和垂直相关系数振荡幅度逐渐增大,水平相关系数振荡周期逐渐减少,而垂直相关系数在接收点靠近海底时不再发生衰减.

5 结论

海底散射声场的空间特性是影响声纳性能的重要参数之一.为了获取海底散射声场的传播损失特性,揭示散射声场空间相关特性与海底粗糙度大小的内在联系,本文基于简正波理论,采用Lambert海底散射模型,并在海面平整、海底粗糙度均匀各向同性的假设下,建立了浅海粗糙海底声散射模型,给出了水平分层介质波导中粗糙海底散射声场声压的简正波表示.利用Monte Carlo 实验和统计处理方法得到一致的散射声场强度,验证了理论模型的正确性.基于本文模型,数值分析了不同粗糙度海底的散射声场空间相关特性,垂直和水平两个特殊方向上声场空间相关特性的数值研究表明,在小起伏度海底条件下相关系数均随阵元间距增大而周期性振荡衰减,并且在垂直方向上,其振荡周期更大,衰减更慢;而随着海底起伏度不断增加,导致散射声场减弱,两个方向上相关系数的振荡幅度幅均会增大,且垂直方向受到的影响更加明显.散射声场空间相关特性的特点意味着应将阵元间距作为声纳设计的重要参数.应用本文模型还可以得到散射声场的复声压,因此为水中随机声场的模拟提供了途径,结合Monte Carlo 方法可以得到水中声场声压振幅与相位的起伏率.

文中所用粗糙海底声散射建模方法很容易推广至粗糙海面声散射建模中,只需将海底散射模型替换为海面散射模型,因此也可以同时考虑随机起伏海面与不平整海底的声散射.由于本文主要内容为粗糙界面散射声场建模,因此界面的散射模型简单选取Lambert 定律,这难免会出现模型适用性降低的情况.在未来工作中,对于不同声速分布、不同海底底质、不同频率、不同海底掠射角,将尝试不同的散射模型,并与实验数据作对比,研究不同散射模型的适用性.