模型预测转矩自抗扰控制下直驱永磁同步发电机最大追踪系统
杨 亚,朱 强, 徐 杰
(1.芜湖职业技术学院 智能制造学院,安徽 芜湖 241006;2.江苏省电力设计院,江苏 南京 210000)
0 引 言
风能是一种高效的可再生能源,它清洁,高效的特点使其具有广泛的使用价值,因此在能源危机愈发严重之际,人们加大了对风能的开发,也使得直驱PMSG的应用研究成为热点[1]。目前使用PMSG进行风力发电的优点主要包括:1)系统的完全可控性,以实现最大风能提取和电网接口;2)实现故障承受和电网支持;3)结构简单。因此,永磁同步发电系统的应用受到越来越广泛的关注。在当前的直驱风力发电系统应用中,PMSG的高性能控制策略主要包括矢量控制和直接转矩控制[2]。直接转矩控制消除了矢量控制中的复杂坐标变换,可以根据发电机速度直接估计最佳转矩设置。它具有快速的转矩和速度响应性能。结合最佳特性曲线方法,直接转矩控制能够精确跟踪系统的最大功率点,有助于进一步提高系统的整体能源利用效率。传统的直接转矩控制采用滞后控制器,因此存在明显的转矩和磁通波动问题[3-4]。众多学者对该问题进行了深入研究,并提出了模型预测控制来优化系统的动态性能。
文献[5]提出一种MPTC来提高船舶永磁同步电机的转矩脉动抑制能力。文献[6]提出一种模型预测控制方法,从而提高了控制系统的动态与稳态控制效果。文献[7]提出一种模型预测双转矩控制,从而降低了系统的计算量,提高了系统的动态性能,同时减小了系统的转矩脉动。文献[8]提出一种模糊MPTC,使得系统的转矩动态响应速度加快,同时降低了转矩脉动。文献[9]针对永磁同步电机,提出一种多矢量的模型转矩控制策略,与传统控制策略相比可以更好地抑制控制系统的谐波电流。文献[10]针对永磁同步电机提出一种基于新型NFTSM控制器的MPTC,可以有效的改善磁链波动与转矩脉动。文献[11]针对五相磁通切换永磁电机开路故障提出一种模型转矩控制,可以进一步实现开路故障容错。文献[12]针对永磁同步电机提出一种改进双矢量的模型转矩控制策略,可以发现改策略可以降低转矩脉动,同时可以更好地提高动态性能。文献[13]针对永磁同步电机提出一种级联式的MPTC策略,与常规策略相比,所提策略可以进一步降低转矩脉动以及磁链波动。文献[14]针对永磁同步电机提出模糊级联法MPTC策略,可以更好地优化动态性能。文献[15]针对永磁同步电机模型预测控制时需要设计权重系数的问题提出标幺化无权重系数MPTC,来消除权重系数,并通过仿真验证所设计方法的有效性。文献[16]针对五相同步电机设计了数阶滑模MPTC,来提高控制系统的性能。文献[17],针对同步电机提出了双矢量无权重MPTC策略,可以进一步降低控制系统的转矩脉动以及磁链脉动。文献[18]针对永磁同步电机设计了一种模型预测控制策略,通过专门设计的评价函数,求解最优化电压矢量使得转矩脉动降低。文献[19]针对永磁同步电机设计了一种具有共模电压抑制能力的模型预测控制策略,可以实现较好的控制性能。通过文献[5-19]可以发现,MPTC具有简单的原理,可以提高系统的动态性能。基于此,本文将MPTC应用于风力发电系统来提高控制系统的电流环的动态性能。
ADRC是在传统PI反馈控制算法的基础上提出的一种新的鲁棒控制设计概念。ADRC器在处理动态不确定性、扰动、非线性等方面也表现出了很好的性能。这最初是文献[20]首次提出,并在文献[21]中得到了充分阐述。它不仅将外部干扰和未知内部动态视为系统的新状态,还通过反馈控制动态补偿干扰。此外,ADRC设计不需要模型参数,使得系统更加简单。文献[22]提出了一种基于传统非线性主动干扰抑制控制的线性ADRC,它不仅继承了传统非线性主动干扰抑制控制的核心优势,而且具有更多的优点。文献[23]提出ADRC在控制基本肢体康复训练中的应用,对系统进行建模与解耦控制,使得系统对内部和外部的抗扰动性能增加,并增加了系统的鲁棒性。文献[24]提出了基于自抗扰理论的最大功率点跟踪策略,提出了一种模型补偿ADRC,从而提高了系统的抗扰动性能。文献[25]针对永磁同步电机控制系统提出一种线性ADRC的速度控制策略,通过注入脉冲的方式来提取位置信号,最后实验验证了所提控制策略可以较好地估计速度,同时具有较好的动态性能。文献[26]针对永磁同步电机控制系统提出一种改进非线性反步自抗扰位置控制策略,可以较好地跟踪位置,从而提高系统控制性能。文献[27]针对永磁同步电机提出一种一阶线性自抗扰与模糊控制相互结合的控制方法,对自抗扰系统中的参数进行在线整定,并与传统的控制策略进行对比,验证了所提控制策略的有效性。文献[28]针对永磁同步电机控制系统提出一种非奇异快速终端滑模自抗扰的复合控制方案,该控制策略可以有效的提高控制系统的动态性能,并减小系统抖振。文献[29]针对永磁同步电机提出一种改进ADRC,其中采用sigfal函数替代扩张状态观测,同时采用线性ADRC替代非线性,并验证了所提控制策略的优越性。从上述文献可以发现,目前ADRC已经成为研究热点,对于ADRC应用也越来越广泛[23-29]。
基于此,本文将MPTC应用于风力发电系统,以解决提高控制系统的电流环的动态性能,并设计了一种综合的补偿ADRC控制策略,旨在解决外部环境突然变化时的速度估计不准确的难题。
1 风力发电系统模型
直驱永磁同步风力发电系统主要由风机、PMSG和变频器组成。叶片捕获的风能被转换为风力涡轮机的输出机械功率为Pm,并驱动PMSG旋转并产生电能Pe,该电能Pe通过电力转换装置输入到电网中。
1.1 风机运行模式
在变速风电系统的实际运行中,由于速度和功率的限制,以及系统机械特性和部件性能的影响,风机通常在3种状态下运行:最大功率捕获、恒定速度和恒定功率。这3种状态对应于图1风机运行模式中的区间a、b、c。其中,vs是切入风速,va是与最大转子速度相对应的风速,vc是额定风速,vx是切出风速,ω是风机的角速度,CP是功率因数。本文主要讨论区间a。
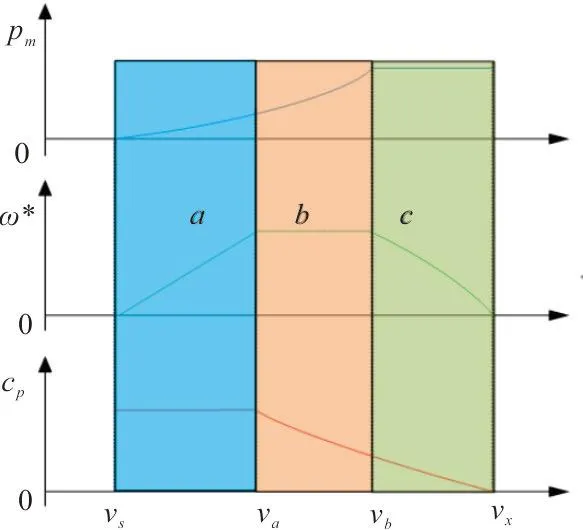
图 1 风机运行模式Fig.1 Operation modes of wind turbine
当风机在vs和va之间的区间运行时,主要采用最大功率跟踪控制。此时,桨距角始终保持在0°附近,并且风力涡轮机被调整为以最佳叶尖速比运行。在这种状态下,功率利用系数总是保持最大值以获得最大功率。
当风机在vs和va之间的区间运行时,主要采用最大功率跟踪控制。此时,桨距角始终保持在0°附近,并且风力涡轮机的速度被调整为以最佳叶尖速比运行。在这种状态下,功率利用系数总是保持最大值以获得最大功率。
1.2 风机空气动力学建模
风力叶轮吸收机械能并转换成如下功率:
Pm=ρπR2CP(λ,β)v3/2
(1)
风力涡轮机转换的机械转矩可表示为
Tm=ρπCP(λ,β)R3v2/2λ
(2)
式中:ρ为空气密度(通常为1.25 kg/m3);R为叶片半径,m;CP(λ,β)为风力涡轮机的功率系数;β为桨距角,(°);λ为叶尖速比。
叶尖速比λ定义为
(3)
式中:ωm为风机的角速度,rad/s;v为风速,m/s。
风力涡轮机的功率系数Cp(λ,β)表示为
exp(-20/λi)+0.006 8λ
(4)
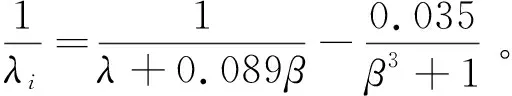
为了进一步研究功率利用率的函数关系,本文在Matlab/Simulink中对函数曲线进行了仿真研究。当β=0和λ=8时,Cp的最大值=0.475。从式(2)中发现Cp(λ,β)中的值越高,风力机可以捕获的风力就越多。故可通过调节叶尖速比,始终保持功率利用系数值最大,从而达到输出功率最大化。因此,PMSG系统在额定风速以下的最大功率控制可以基本等效PMSG的速度控制。
1.3 PMSG动力学方程
参考系中的电磁转矩可以表示为
Te=3/2p(ψdiq-ψqid)
(5)
式中:p为极对数。
转换d-q参考系中的模型,得出PMSG的动力学方程如下:
(6)
然后将定子磁链表示为
(7)
式中:ud、uq为参考系中的定子电压;id、iq为转换d-q参考系的定子电流;ψf为磁通量;Rs为定子电阻;ωr为非凸极PMSG的转子电角速度,Ld=Lq=L。
PMSG的力学方程表示为
(8)
式中:J为转动惯量,kg·m2;B为PMSG和涡轮机的组合黏性动摩擦因数。
2 控制策略
2.1 模型预测转矩控制器的设计
MPTC主要使用模型来预测转矩的大小,并使用成本函数来选择相应的电压矢量,以最小化参考转矩和控制转矩之间的差异。模型预测的优点主要是总谐波失真低和对参数变化的抵抗力强。为了在动态和稳态下获得更好的性能,采用式(9)所示的最小化成本函数,其可以描述为
(9)
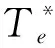
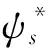
(10)
式中:Ls是定子电感。
根据等式(6),预测模型的定子电流可以以离散时间形式描述如下:
(11)

根据等式(7),在d-q参考系中,预测模型在采样期内(k+1)Ts的定子磁链和转矩可以描述为
(12)
因此,转矩的估计如下所示:
(13)
2.2 改进型速度环自抗扰器设计
PMSG的速度输出可以表示为
dωm/dt=(Tm-Te-Bωm)/J
(14)
式中:Te电磁转矩。将e(t)视为集中扰动,它包括系统的内部动力学与外部扰动相结合,可以表示为
e(t)=(Tm-Bωm)/J+(m+m0)Te
(15)
式中:m是m0的估值,m0=1/J。
式(14)可以改写为
dωm/dt=e+m0Te
(16)
因此PMSG的ADRC可以表示为
(17)
其中ADRC的控制律可以设计为
(18)
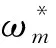
通过式(14)可以发现,集中扰动受到负载转矩以及考虑到风电系统中黏性动摩擦因数随转速的变化会有细微变化,同时负载转矩在不断的变化。而实验前可以通过对实验电机进行实验拟合,最终可以等效为B=B0+Awm的形式,其中B0、A为拟合的常数。
由于电机中安装了速度传感器,dwm/dt为已知量,微分也为已知量。通过对转动惯量J和阻力系数B的辨识,根据计算出的Te(k)值同时估测Tem,此时将式(14)改写为
(m0+m)Te
(19)
式中:Tem、Be用于估计Te、B。
因此,改进型ADRC可以表示为
(20)
改进ADRC控制律可以设计为
(21)
基于MPTC的改进型ADRC策略如图2所示。
图2所提出控制方法主要包括风力涡轮机的建模,PMSG建模以及控制策略。其中所提控制策略部分主要包括转速环为改进的ADRC。通过参数计算,可以变换Be以及Tem,然后引入到ADRC中来改善其估计性能。同时ADRC输出为给定转矩,根据式(10)获得给定的磁链,此时根据模型预测理论原理,可以实时获取当前的转矩以及磁链,进一步根据式(9)所定义的曲线函数来确定最佳的电压矢量来控制IGBT的导通与关断。
3 模拟结果和讨论
为了验证这种控制策略的优越性,将MPTC与改进型ADRC+MPTC进行了比较。MTPC控制策略为:速度回路采用PI,电流回路采用MPTC;MPTC+改进型 ADRC策略为:参数补偿改进型自抗扰用于速度回路,MPTC用于电流回路。其中风力涡轮机中的最佳叶尖速比设置为8,涡轮机叶片半径设置为1.5 m,最大功率系数根据前文得到为0.475,在设计PMSG系数时,定制电感L设计为7.2 mH,永磁体磁链设计为0.175 Wb,定子电阻设计为1.3 Ω,极对数设计为4,同时系统的额定电压设计为350 V。
本文采用渐变风速、随机风速、阵风风速和杂波风速来模拟风速,并对这4种风速下的模型预测转矩ADRC策略进行了模拟仿真。
杂波风是渐进风、基本风和随机风以及阵风的组合。接下来,进行几种风速的对比验证。
3.1 风速变化不大的模拟对比
本文中,图3(a)、(b)显示了渐变风以及阵风下2种控制策略的速度跟踪效果。
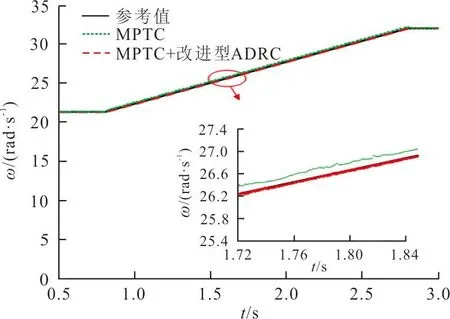
(a) 渐变风
渐变风表现出风速缓慢变化的特点。图3(a)显示了在该风速下2种控制策略的速度跟踪效果。从图3(a)可以看出,当遇到渐变风时,此时采用MPTC控制时,可以发现MPTC下与参考值之间会有0.2 rad/s的静态误差;而遇到渐变风时,此时采用MPTC+改进型 ADRC控制时,此时可以发现MPTC+改进型 ADRC下的波形与参考值几乎没有静态误差。
阵风具有风速突变的特点,所以阵风可以用余弦函数来表示。图3(b)显示了2种控制策略在该风速下的速度跟踪效果。从图3(b)可以看出,当遇到阵风时,此时采用MPTC控制时,可以发现MPTC下与参考值之间会有一定的静态误差,而采用MPTC+改进型 ADRC控制时,MPTC+改进型 ADRC下的波形与参考值静态误差很小。
3.2 风速变化较大的模拟对比
杂波风由上述4种风组成,具有较强的突变性和随机性,采用参考值1表述。随机风速可以用来模拟风速的随机性,采用参考值2表述。图4显示了2种控制策略在杂波风和随机风速下的速度跟踪效果。

图 4 风速较大时的跟踪性能Fig.4 Tracking performance at highwind speed
从图4可以看出,当系统在遇到杂波风时,此时采用MPTC策略时,会有较大的波动,严重时误差会达到5 rad/s,控制系统跟踪效果会严重降低,使得系统无法获得较好的跟踪效果;当系统在遇到杂波风时,而采用MPTC+改进型ADRC策略时,可以发现,系统跟踪性能良好,不会出现较大的速度超调等问题,具有较好的跟踪效果。当系统在遇到随机风时,此时采用MPTC策略,在随机风下误差最大会达到3 rad/s,使得系统无法达到一定的跟踪效果;当采用MPTC+改进型 ADRC时,可以发现,系统跟踪性能保持较好的状态,具有较好的跟踪效果。
4 结 语
本文提出了一种风电系统PMSG的模型预测转矩ADRC方法。为了捕获最大功率,本文提出了一种新的跟踪策略。该策略将改进型ADRC与MPTC相结合,并对几种风速进行了仿真对比。仿真结果表明,该控制策略能够有效地解决不确定的动态特性和对外部扰动的抵抗,保持了较好的抗扰动能力和鲁棒性,具有良好的动态性能。本文主要对所提出的新的控制方法进行了理论与仿真验证,但是缺乏一定的实验验证,因此在接下来的工作中将开始搭建实验平台,并进行有效的实验验证。

