黄河下游河道悬沙与床沙粒径智能预测研究

董庆豪 孙龙飞 王远见 赵万杰

关键词：泥沙粒径；变量筛选；机器学习；智能预测；黄河下游河道

0引言

悬沙和床沙颗粒级配是影响泥沙运动的重要因素，黄河下游河道的淤积，不仅取决于来白中游泥沙的数量，而且受来沙颗粒级配的影响。探究黄河下游河道悬沙和床沙颗粒级配变化，有助于分析泥沙整体淤积情况，同时能够反馈指导优化水库运用方式，为水库的调度提供重要依据。

目前，针对黄河下游河道悬沙和床沙颗粒级配的研究，主要集中于小浪底水库运行前后悬沙和床沙粒径的时空变化特征和规律。其中：孙维婷等通过各水文站多年泥沙数据．分析了黄河悬移质泥沙粒径的时空变化特征，得到各水文站悬移质年平均中数粒径变化趋势不一致的结论：Hou等分析了黄河下游典型断面2004-2015年河道床沙和悬沙年平均中数粒径沿河道方向的变化趋势：陈建国等统计1999年和2009年黄河下游各河段床沙中数粒径的平均值，得出10a来黄河下游河床表面泥沙粒径普遍增大1倍以上的结论；付春兰等分析小浪底水库运用前后黄河下游水沙条件的变化，结果表明自2002年调水调沙后，河床质中数粒径逐渐粗化：薛博文等研究了不同时期黄河下游泥沙粒径变化情况，分析了其对小浪底水库调水调沙的响应规律。上述研究虽然很好地分析了悬沙和床沙粒径的时空变化规律，但由于影响泥沙粒径变化的因素较多，因此根据时空变化规律仍难以准确预测悬沙和床沙粒径。此外，在泥沙粒径变化预测方面，现有研究多采用理论公式进行床沙粒径的分析，这些理论方法计算过程复杂或有特殊适用条件，具有一定局限性。

机器学习作为人工智能中的一项重要技术，可从大量数据中挖掘变量间存在的复杂映射关系，已广泛应用于各个科学领域，且取得了良好的应用效果。其中，在水利预测方面，Aires等使用机器学习算法预测多西河流域泥沙浓度，采用变量选择算法对变量进行筛选，取得良好的预测效果：鲍振鑫等耦合VIC模型和8种机器学习算法构建了输沙量模拟模型，能够较好地模拟月输沙量过程；Han等提出一种结合输入层和隐藏层两种注意力机制的LSTM模型AT-LSTM，用于宜昌站和屏山站的长期径流预测；Yang等提出了基于小样本学习的LSTM-原型网络融合模型预测长期径流，并在两个数据稀缺地区验证了模型的有效性。目前，机器学习算法在预测泥沙浓度、输沙量、径流量等方面应用较多，但尚缺乏针对悬沙和床沙粒径预测的相关研究。

笔者利用黄河下游河道花园口等6个断面的水沙系列数据，进行悬沙和床沙粒径主要影响因子的筛选，并基于机器学习算法构建黄河下游不同断面的悬沙和床沙粒径的预测模型，以期为实现泥沙粒径的准确预测提供新的思路。

1研究区域及数据来源

黄河下游以桃花峪为起点至人海口，河长786km，流域面积占黄河流域总面积的3%．河道坡降小，水流平缓，泥沙淤积严重，河床升高形成地上“悬河”。本文选取下游花园口、夹河滩、高村、孙口、泺口、利津6个断面（水文站），开展不同断面泥沙粒径预测研究。收集整理2006-2020年黄河小浪底水库月均出库流量、出库含沙量数据，下游花园口等6个水文站月均流量、含沙量、流速、河宽、水深、比降、水位以及悬沙和床沙中数粒径、平均粒径等数据，数据均来源于黄河水利委员会编制的《黄河流域水文资料》。

2研究方法

首先选取泥沙粒径主要影响因子，并通过变量筛选算法确定机器学习模型输入的变量组合：然后基于不同机器学习算法建立预测模型：最后对模型预测结果进行分析评估。

2.1主要变量筛选

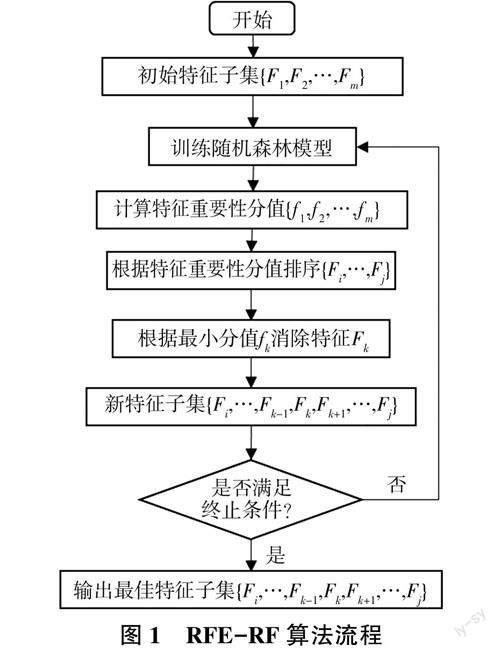
黄河下游河道悬沙和床沙粒径变化主要受来水来沙条件（流量、流速、含沙量）、河道边界条件（河宽、水深、比降）等多种因素的影响。为有效提取机器学习模型最佳输入变量组合，采用递归特征消除算法结合随机森林（RFE-RF）算法进行变量筛选，消除冗余变量，确定变量组合。RFE-RF算法把需要的特征集合初始化为数据集，采用R软件Caret包中的varlmp函數计算影响因子的重要性分值并进行排序，每次剔除一个重要性分值最低的特征，直到所有特征都被剔除，并通过模型对不同个数特征的子集进行评估，输出最佳特征子集。RFE-RF算法流程如图1所示。

2.2算法原理

本文采用K最邻近（KNN）、随机森林（RF）、支持向量回归（SVR）3种机器学习算法建立预测模型，各算法的原理如下。

1）KNN算法的核心思想是数据库模式匹配，即从历史数据库中提取数据特征，根据合理的状态向量找到与当前实时观测数据相匹配的k个近邻数据，将其作为输入变量以预测后续状态数据值。

2）RF算法是一种通过集成学习思想将多棵树集成的算法，其基本单元是决策树，并利用多棵决策树对样本进行训练及预测。

3）SVR算法是运用支持向量机（SVM）解决回归问题的算法。与传统的回归算法不同，SVR不仅考虑了数据的拟合程度，而且考虑了模型的泛化能力，能够有效地处理高维数据和非线性数据。SVR算法的基本思想是将数据映射到高维空间中，通过寻找最优的超平面来实现回归。

2.3模型构建

综合考虑水沙、河道边界等条件，悬沙和床沙粒径的主要影响因子包括小浪底水库出库流量、出库含沙量，以及下游6个水文站的流量、含沙量、平均流速、最大流速、河宽、平均水深、最大水深、河床比降、水面比降和水位等共12个变量。

各断面不同粒径预测模型建立的主要步骤如下：1）选择2006-2019年月均数据集进行变量筛选，使用筛选后的影响因子作为模型输入变量，其中悬沙粒径影响因子选取当月月均数据：床沙粒径影响因子筛选考虑滞后性，通过相关性分析，确定其滞后时间，并采用滑动平均法计算各影响因子的月均数据。2）将2006-2019年月均数据集按照4：1的比例划分成训练集和测试集。3）将训练集代人3种不同机器学习算法分别进行训练并建立预测模型。4）将测试集代入模型中，通过决定系数R2、均方根误差RMSE、平均绝对误差MAE指标评估不同算法模型的预测效果，并选出各断面预测效果最好的模型。5）将2020年数据集分别代入选出的各断面最优模型，通过R2值和显著性检验进一步验证所建模型的性能。

3实例结果分析

3.1泥沙粒径关键影响因子提取

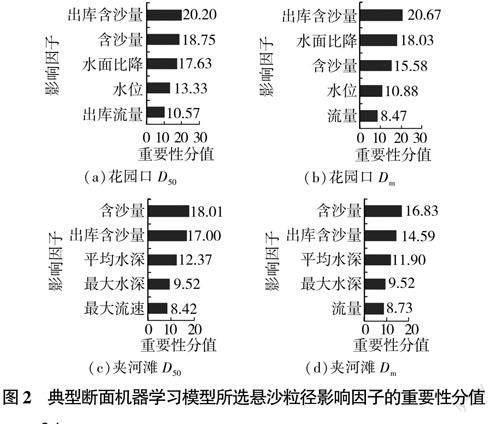
采用变量筛选方法，得到各断面悬沙和床沙粒径重要性分值排序前5的影响因子，以花园口、夹河滩断面为例，其结果分别如图2和图3所示（D5o表示中数粒径，D表示平均粒径）。

各断面经筛选后变量的数量为6～9个，有效减少了初始变量的数量，有利于提取主要影响因子。由图2和图3可见，对于黄河下游悬沙粒径预测，大部分断面的来沙条件因素重要性分值较高，对粒径变化的影响较大，且不同断面及同一断面不同粒径所选取的影响因子之间存在差异；而对于黄河下游床沙粒径预测，同一断面不同粒径重要性分值排序前5的影响因子基本相同，但不同断面之间影响因子重要性分值差异较为显著。

3.2预测结果分析

3.2.1悬沙粒径预测结果

根据各断面不同粒径影响因子的筛选结果，采用筛选后的变量作为模型的输入变量构建预测模型，最终所得不同机器学习算法模型在测试集上的评估指标，见表1。

由表1可知，对于下游河道悬沙粒径，机器学习模型在各断面测试集预测方面的整体适用性较好，预测值误差较小。不同机器学习算法预测结果的误差存在差异，其中KNN模型的RMSE均在0.0095mm以下、MAE均在0.0079mm以下，RF模型的RMSE均在0.0085mm以下、MAE均在0.0068mm以下，SVR模型的RMSE均在0.0115mm以下、MAE均在0.0086mm以下。相比之下，RF算法建立的模型在悬沙粒径预测方面对于各断面预测结果的误差均较小，各断面优选模型均为RF算法建立的模型。

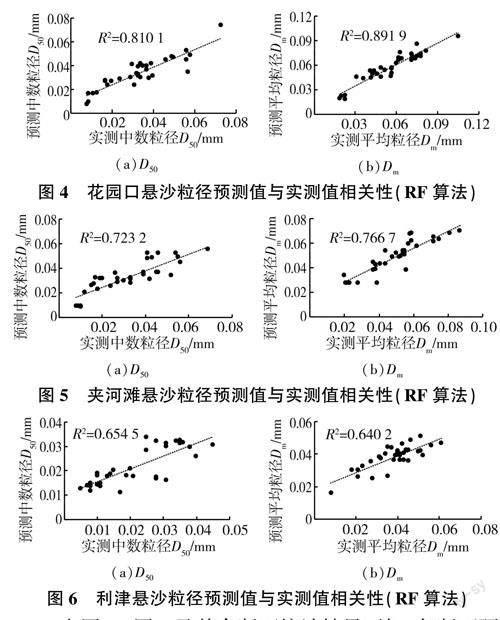
此外，统计由表1选出的各断面在测试集上综合效果最好的模型，得到预测值与实测值之间的相关性，以花园口、夹河滩、利津断面为例，其悬沙粒径预测值与实测值之间相关性如图4～图6所示。

由图4～图6及其余断面统计结果可知，各断面预测值与实测值R2均在0.64～0.89之间，相关性良好，模型拟合程度较高。

为进一步验证所建立模型的效果，选取各断面优选模型分别对2020年悬沙月均粒径进行预测，各断面2020年悬沙粒径实测值与预测值综合相关性如图7所示。由图7可见，所得实测值与预测值之间R2达0.6097，进一步表明模型对于悬沙粒径具有良好的預测准确性。

3.2.2床沙粒径预测结果

与悬沙粒径类似，对于床沙不同机器学习算法模型在测试集上的评估指标见表2。

由表2可知，对于下游河道床沙粒径，机器学习模型在不同断面测试集上的预测误差存在较大差异，考虑其与床沙粒径空间分布不均有关，但整体上各断面优选模型的RMSE最高为0.0448mm、最低为0.0109mm，MAE最高为0.0308mm、最低为0.0086mm，3种机器学习算法在不同断面床沙预测中具有较好的适用性。

统计由表2选出的各断面在测试集上综合效果最好的模型，得到预测值与实测值之间的相关性，花园口、夹河滩、泺口断面床沙粒径预测值与实测值之间相关性如图8～图10所示。

由图8～图10及其余断面统计结果可知，各断面预测值与实测值R2均在0.37～0.72之间，不同断面之间存在显著差异。花园口断面中数粒径，夹河滩断面、孙口断面粒径R2在0.5以下，其余断面粒径R2在0.5以上，而泺口断面粒径R2达0.7，表明模型预测值与实测值的相关性及拟合效果整体上较好。

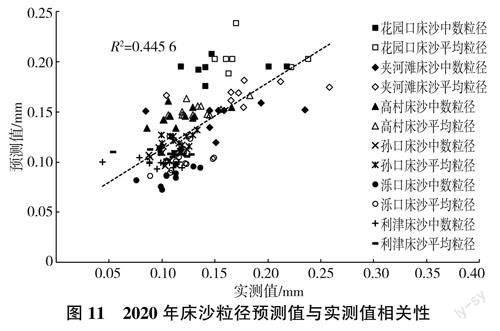
进一步验证所建立模型的效果，由各断面的优选模型分别对2020年床沙月均粒径进行预测，各断面2020年床沙粒径实测值与预测值综合相关性如图11所示。

由图11可见，预测值与实测值之间R2达0.4456，预测结果偏小，其原因可能是床沙组成的调整是一个缓慢过程，是下泄水沙过程与床面边界之间长期相互作用的结果，影响因素和涉及信息远较悬沙的复杂。尽管从结果上看床沙粒径预测精度较悬沙的差，但整体上预测值与实测值仍较为接近，结果可以接受。

4结论

为系统掌握黄河下游河道悬沙和床沙粒径的分布规律，克服泥沙粒径预测理论方法复杂或有特殊适用条件的局限性问题，本文综合考虑不同影响因素，采用变量筛选算法进行变量筛选，并基于机器学习算法进行泥沙粒径预测。实例分析结果表明，变量筛选算法能够减少冗余及不相关变量，构建最优特征子集。优选模型对悬沙粒径预测效果良好，在测试集上各断面预测值与实测值R2在0.64～0.89之间：床沙粒径预测精度较悬沙相对偏低，在测试集上各断面预测值与实测值R2在0.37～0.72之间。进一步验证优选模型效果，在对2020年月均泥沙粒径进行预测时，悬沙粒径R2可达0.6097，模型拟合相对较好；床沙粒径R2为0.4456，总体上结果可以接受。

整体而言，应用机器学习算法构建预测模型能够较好实现黄河下游河道泥沙粒径的准确预测，可以为黄河调水调沙提供参考。