The Weighted Basis for PHT-Splines
Zhiguo Yong,Hongmei Kang and Falai Chen
1School of Mathematical Sciences,Soochow University,Suzhou,215006,China
2School of Mathematical Sciences,University of Science and Technology of China,Hefei,230026,China
ABSTRACT
PHT-splines are defined as polynomial splines over hierarchical T-meshes with very efficient local refinement properties.The original PHT-spline basis functions constructed by the truncation mechanism have a decay phenomenon,resulting in numerical instability.The non-decay basis functions are constructed as the B-splines that are defined on the 2×2 tensor product meshes associated with basis vertices in Kang et al.,but at the cost of losing the partition of unity.In the field of finite element analysis and topology optimization,forming the partition of unity is the default ingredient for constructing basis functions of approximate spaces.In this paper,we will show that the non-decay PHT-spline basis functions proposed by Kang et al.can be appropriately modified to form a partition of unity.Each non-decay basis function is multiplied by a positive weight to form the weighted basis.The weights are solved such that the sum of weighted bases is equal to 1 on the domain.We provide two methods for calculating weights,based on geometric information of basis functions and the subdivision of PHT-splines.Weights are given in the form of explicit formulas and can be efficiently calculated.We also prove that the weights on the admissible hierarchical T-meshes are positive.
KEYWORDS
PHT-splines;partition of unity;weighted bases;PHT-splines;subdivision
1 Introduction
Polynomial splines over hierarchical T-meshes(PHT-splines for short)[1]are a kind of globalC1continuous polynomial splines that can be locally refined.PHT-splines possess a very efficient local refinement algorithm and inherit many good properties of T-splines such as adaptivity and locality.PHT-splines are now widely applied in adaptive geometric modeling[2–4],adaptive finite element[5],iso-geometric analysis[6–13]and topology optimization[14].
With further in-depth application,the improvement of PHT-splines has also been underway.One of the limitations of PHT-splines is the restrictions from hierarchical T-meshes,which require the underlying meshes to start with tensor product meshes and be refined by inserting crosses.The generalization of PHT-splines on general T-meshes[15]and modified hierarchical T-meshes(allowing split-in-half in mesh refinement) [16] is precisely aimed at overcoming the restrictions from meshes.Another improvement regard to PHT-splines is the construction of basis functions.The original basis functions[1]have a decay phenomenon(the function values decay as the level increases)when the level difference is big in the underlying support.The decay of basis functions when applied in iso-geometric analysis leads to ill-conditioned stiffness matrices,and thus unstable numerical solutions.A new set of basis functions is defined by the B-splines that defined on the 2×2 tensor product meshes associated with basis vertices [2] to overcome the decay phenomenon that occurs in basis functions,but at the cost of losing the partition of unity.
The partition of unity is a default ingredient in the construction of approximating functions in finite element methods [17–19].Moreover,in the field of topology optimization [14],the density variable takes value in the range of[0,1].The basis functions that form a partition of unity are more suitable for designing density variables that meet the range condition.In this paper,we aim to provide basis functions that form a partition of unity and also have no decay phenomenon,facilitating more effective applications for PHT-splines.
The truncation mechanism is a common way of constructing basis functions for hierarchical spline spaces that form a partition of unity,such as the original PHT-splines[1],THB-splines(the truncated hierarchical B-splines) [20] and truncated T-splines [21].But as mentioned above,the truncation mechanism causes the decay in basis functions.In this paper,we will show that the basis functions that form the partition of unity and have no decay can be constructed without the truncation mechanism.The weighted bases that satisfy the required properties are defined by the bases constructed in[2] multiplied by positive weights.The weight for each basis function can be computed explicitly and efficiently based on the geometric information of the basis function.Moreover,when the level difference is not greater than 2,the weights can also be computed by the PHT subdivision scheme.
In[22],the authors also proposed a method to define new basis functions to overcome the decay problem and guarantee the partition of unity.However,their method only considers specific cases that the original truncated basis functions have rectangular supports,in which case they are replaced by the associated tensor product B-splines.Instead,our method is more versatile and can be applied to arbitrary T-meshes easily.
The rest of this paper is organized as follows.In Section 2,some basics of PHT-splines are reviewed.In Section 3,we introduce the weighted bases in detail.In Section 4,the subdivision scheme of PHT-splines is introduced as an alternative algorithm for calculating weights.In Section 5,some hierarchical T-meshes are demonstrated to verify the effectiveness of the proposed method.Finally,we conclude the paper with a summary in Section 6.
2 PHT-Splines
In this section,we give a brief review of the definition of PHT-splines.The readers are recommended to refer to[1]for more details.
2.1 Definition of PHT-Splines
Given a T-mesh T,Fdenotes all the cells in T andΩdenotes the region occupied byF.The polynomial spline space over T is defined as
where Pmnis the space of all the polynomials with bi-degree(m,n),andCα,β(Ω)is the space consisting of all the bivariate functions which are continuous inΩwith orderαin thex-direction and with orderβin they-direction.In particular,in the case ofm≥2α+1,n≥2β+1,S(m,n,α,β,T)is well studied and its dimension is given in[23].
PHT is defined byS(3,3,1,1,T)with T being a hierarchical T-mesh.Here,a hierarchical T-mesh is a special type of T-mesh that has a natural hierarchical structure and defined in a recursive fashion.One generally starts from a tensor product mesh(level 0).From levelkto levelk+1,a cell at levelkis subdivided into four sub-cells which are cells at levelk+1.
The dimension formula of PHT has a concise expression with
whereVbandV+represent the number of boundary vertices and interior crossing vertices in T respectively.As defined in[1],a boundary vertex or an interior crossing vertex is called a basis vertex.This dimension formula implies that each basis vertex should be associated with four basis functions.Thus,the construction of PHT is to construct four bicubicC1,1continuous functions for each basis vertex so that the functions span the PHT and retain some good properties.
2.2 Basis Construction
The original PHT basis functions are constructed by truncation mechanism in [1] level by level in order to make basis functions vanish at other basis vertices.Fig.1 shows two typical hierarchical meshes,where the basis functions associated the marked vertices have undesired decay as level increases.In Fig.1a,the maximum values decay rapidly as the level increases.In Fig.1b,the maximum value does not decrease,but the basis function decays sharply along the refinement direction as level increases.This decay phenomenon of basis functions is first noted in[2].The decay phenomenon makes the stiffness matrix have large condition number and thus produces unstable solutions.
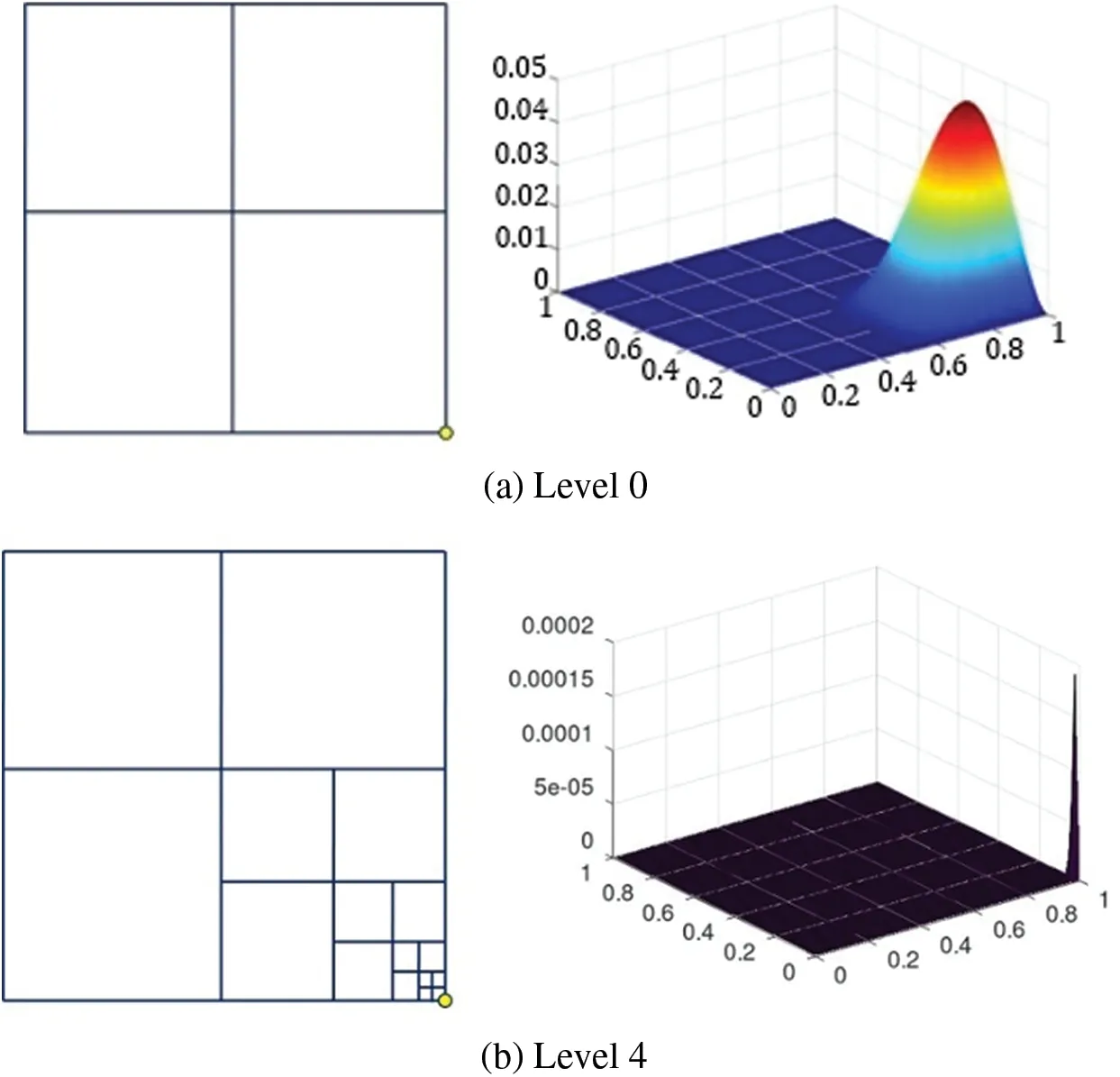
Figure 1 : (Continued)
Figure 1 :The decay phenomenon of PHT-spline basis functions associated with the vertex marked by a yellow circle
A new basis functions are proposed in[2]to amend the decay phenomenon.In the following,we give a brief review of the construction.
Definition 1Supposevis a basis vertex in T,the support mesh ofv,denoted byTv,is defined as the minimal 2×2 tensor product mesh,wherevis the central vertex and all edges are subordinate to T.
Note that ifvis a boundary vertex,the support mesh is actually a 2×1,1×2 or 1×1 tensor product mesh.For any given hierarchical T-mesh,the support mesh of each basis vertex exists and is unique.The support mesh can be found efficiently.
Fig.2 illustrates the support meshes of six basis vertices including three boundary vertices and three interior crossing vertices,where the six basis vertices are marked by solid circles and the corresponding support meshes are marked by bold lines.
The basis functions associated with a basis vertex are then defined by the four B-spline functions that defined on the support mesh.Specifically,for a basis vertexv=suppose the support mesh is defined bythen the four bases are defined as follows:
These four basis functions are linearly independent and have the same supportThis way of definition has been confirmed in[2]without decay phenomenon.
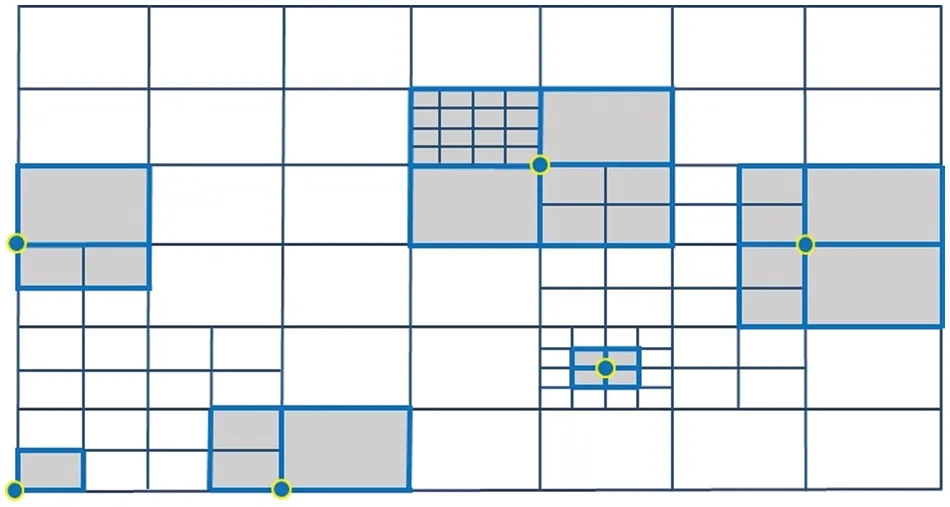
Figure 2 :Support meshes of six basis vertices
3 Weighted Bases for PHT-Splines
3.1 Geometric Information
For any basis functionb(s,t),we define a geometric information(the function value,the first order partial derivatives and the mixed partial derivative)operator by
For a basis vertexv=,the associated four PHT-splines basis functions are defined by(3).We collect the geometric information ofb0,b1,b2,b3at the basis vertex v into the matrixG,
where
The sum of the geometric information of the four basis functionsb0,b1,b2,b3at the associated basis vertex is equal to(1,0,0,0),because the sum of the four basis functions is identically equal to 1.This can also be verified by the column sums inG.As non-vanishing basis functions at basis vertices are not limited to the associated four basis functions,so the basis functions defined in[2]do not form a partition of unity generally.
Suppose that the maximal subdivision level of T isNand Tkdenotes the hierarchical T-mesh at levelk,k=0,···,N.Then we have T=TN.For a basis vertexv,ifv∈Tkbutv/∈Tk-1,then it is called a basis vertex at levelk,k=1,···,N.Specially,every vertex in T0is a basis vertex at level 0.Theith basis vertex at level k is denoted byand the four basis functions associated withvkiare denoted as,j=0,1,2,3.
According to the definitions of support meshes and hierarchical T-meshes,the basis function proposed in[2]has the following property:
· A basis vertex at levellcan not be in the interior of the support of any basis function at levelk>l,that is
wherenkandnlare the number of basis vertices on levelkandl,respectively.
· The basis functionsbk4i+jvanish at the basis vertices on level k,except for the vertices associated with them,that is
3.2 Computing Weights
The proposed weighted bases are defined by multiplying the basis functions constructed in [2]by positive weights.This ensures that the weighted bases not only have no decay,but also form the positive partition of unity.In the following,we are going to compute weightswl4i+j>0 for each basis function such that
This problem can be understood as the PHT fitting problem of a constant function.Since a PHTspline space spans the bicubic polynomial space P33,the weightswl4i+jsatisfying(9)exist.As described in[1],the control points of the PHT-spline surface,here we call them weights,can be determined based on the geometric information at the basis vertices.
The weights are computed level by level.First,we evaluate the PHT-spline surface at the basis vertices on level 0,that is
since the basis functions on levell>0 vanish on any basis vertex on level 0.Furthermore,B-spline basis functionsb04g+j,j=0,1,2,3 form a partition of unity,thus we obtainw04g+j=1,forj=0,1,2,3 andg=1,···,n0.
For a basis vertexvkgon levelk>0,the non-vanishing basis functions atvkgare composed of two parts: the non-vanishing basis functions atvkgon levell<kand the four basis functions associated withvkg.The indices of basis vertices associated with the first part are denoted byK,
and the weighted sum of the basis functions inKis denoted byh(s,t),
Because the geometric information operator is linear,one has
Thus,the weights of the four basesbk4g+jare determined by the following linear equations:
The matrixGis invertible,so the solution of(13)exists and is unique.Specifically,the weights are explicitly expressed by
The non-vanishing basis functions atvkgcan be found easily owing to the simple construction.The weights can be computed explicitly based on (14) without the need to solve a linear system of equations.
Fig.3a shows a typical hierarchical mesh where the diagonal elements are refined.The support meshes of some marked basis vertices are shaded in orange color.We discuss the weights of the basis functions associated with colored vertices.
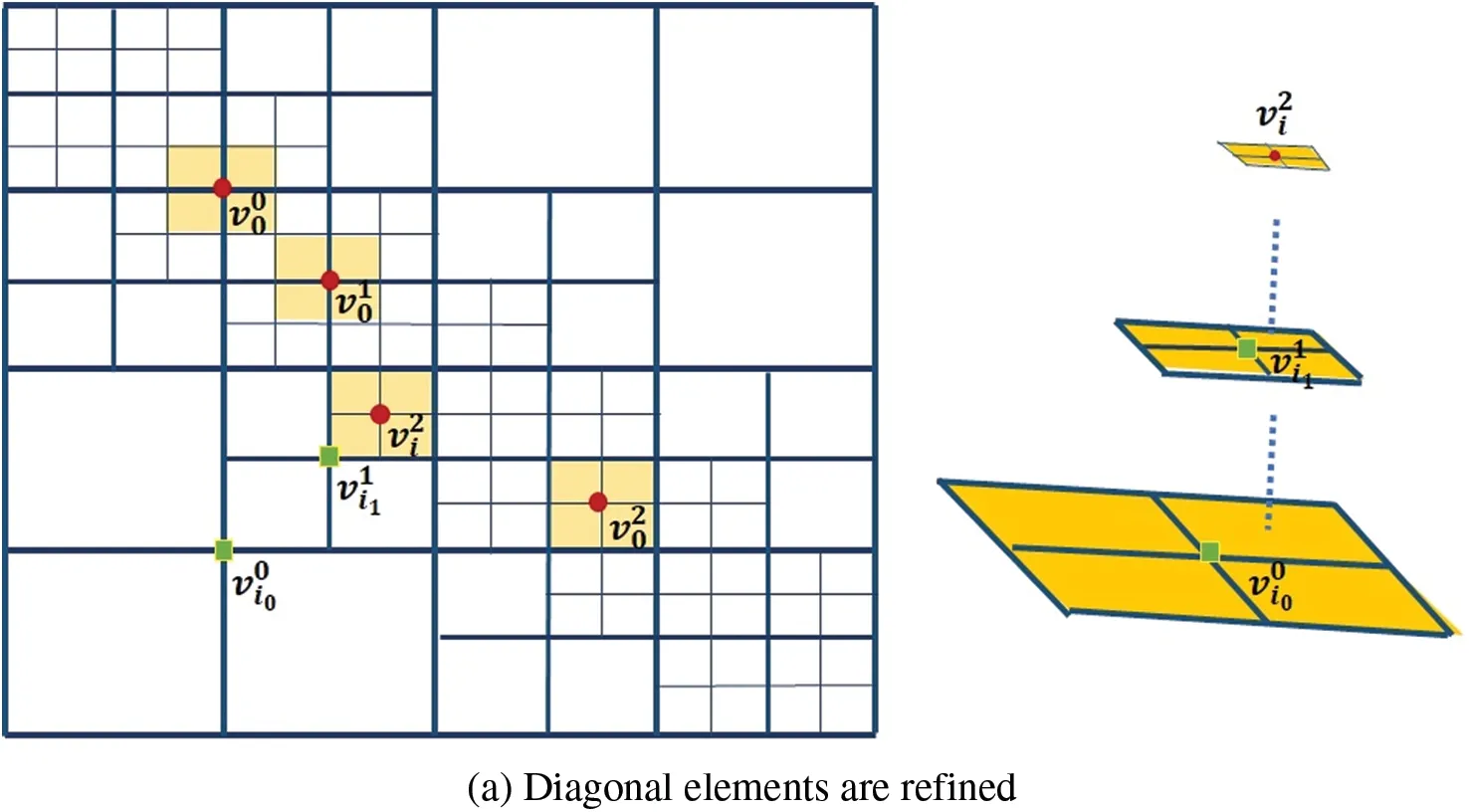
Figure 3 : (Continued)
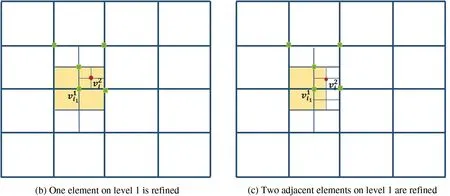
Figure 3 : (a) The weights associated v00,v10,v20 (marked by red circles) are all equal to [1,1,1,1].The weights for are equal to .There are two non-vanishing basis functions(associated with the vertices marked by green squares) at (b) One element on level 1 is refined.The weights associated are equal to[0,0,0,0].(c)The weights associated are equal to[0.5625,0.1875,0.1875,0.0625]
· The weights ofv00,v10andv20(marked by red circles) are all equal to [1,1,1,1],since all basis functions are zeros at these three vertices,except for the basis functions associated with themselves,which meansh(s,t)≡0.
· The weights forare computed as follows: (1) the right termh(s,t)=since only the support ofcontains; (2) the elements inGare constructed with Δs1=Δs2=0.125,Δt1=Δt2=0.125,λ=μ=,α=β=4,based on(6).To sum up,
· The non-vanishing basis functions atv2i(marked by red circles)are denoted byand(marked by green squares).The weighted sum is expressed as
Submittingh(s,t)into(14),the weights associated withv2iare equal to
Fig.3b shows a case where the weights forv2iare equal to [0,0,0,0].The non-vanishing basis functions onF(the refined element)are also the non-vanishing basis functions atv2i.Notice that the weights on level 1 are computed such that the basis functions form a partition of unity,soh(s,t)|F≡1,which means the right term in(14)is a zero vector.SinceGis invertible,the weights associated withare thus zeros.
The basis functions correspond to zero weights has no contribution in the entire representation.Notice that zero weights occur if and only if the function g form a partition of unity on the domain occupied by the support mesh of the considered basis vertex.Therefore,to avoid this,the isolated refined elements,like the case in Fig.3b,are not allowed.
In Fig.3c,two adjacent elements are refined.The support ofis shaded by yellow color in Figs.3b and 3c.The support ofin Fig.3c becomes smaller,thush(s,t) do not form a partition of unity onFanymore.Therefore,the weights forv2iare non-zeros.
Based on the above analysis,we made the following assumptions for the hierarchical T-mesh to define positively weighted bases that form a partition of unity.
Definition 2A hierarchical T-mesh is called an admissible hierarchical T-mesh if there are not any isolated refined elements in the hierarchical T-mesh.If an element on levellis refined,but none of its adjacent elements are refined,it is called an isolated refined element.Here,if two elements of the same level share at least one edge,they are called adjacent elements.
Figs.3a and 3c are two admissible hierarchical T-meshes,while Fig.3b is not an admissible hierarchical T-mesh.A hierarchical T-mesh can become an admissible hierarchical T-meshes by performing refinement on adjacent elements of isolated refined elements.
To ensure the refinement is highly localized,we generally require the refinement level between any two neighboring elements cannot be greater than one,which is also required in[18].Under this requirement,hierarchical T-meshes are admissible.
Proposition 1There uniquely exists a set of positive weights for the bases constructed in[2]on the admissible hierarchical T-mesh such that the weighted bases form a partition of unity,that is there uniquely existsw1,w2,···,wn>0 such thatwibi(u,v)≡1 for(u,v)∈[a,b]×[c,d].
ProofThe existence and uniqueness of the weightswl4i+jare implied by the linear system(13).In the following,we only provewl4i+j>0.
For the basis functionsb0iassociated with the basis vertices on level 0,the functionh(s,t)defined in(11)is equal to zero,i.e.,h(s,t)=0,then the weights solved by(13)are all equal to ones.
For an elementFin the initial mesh T0,we denote the B-spline functions associated with the four corners ofFbyb4i0+j,b4i1+j,b4i2+j,b4i3+j,j=0,1,2,3.Remember that these basis functions are defined over T0,instead of the final hierarchical T-mesh T.Then,the non-vanishing basis functions onFare only these basis functions,which also form a partition of unity onF.As the refinement proceeds,the supports of some of these basis functions are changed,and some new basis functions are added.The PHT-spline space defined over T0are contained in the PHT-spline defined over T,thenb4i0+j,b4i1+j,b4i2+j,b4i3+jcan be exactly represented by the basis functionsbl4i+kon levellby knot insertion algorithm,that is,forj=0,1,2,3,
Since
then
This implies that the weights
In Fig.4,we show the PHT surfaces defined over the same hierarchical T-mesh and by the same control points,but using different bases: the proposed weighted bases and non-decay bases [2].The control points are designed on the planez=1.We see that the PHT surface defined by weighted basis functions form a partition of unity.
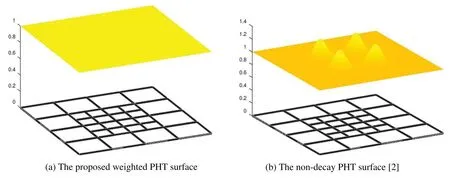
Figure 4 :The weighted PHT-splines proposed in this paper form the partition of unity,while the PHTsplines defined by the non-decay bases[2]cannot form a partition of unity
We conclude the method of computing the weights such that the weighted basis functions form a partition of unity in Algorithm 1.

Algorithm 1:Calculation of weights Input:k-th level hierarchical T-mesh with basis vertices set V while vi ∈V Find the support mesh of vi and compute α,β,λ,μ based on the formula(6);Find all the basis functions that are not equal to zeros at vi and get h(s,t)defined by(11);Calculate the weight wk 4i+j of vi according to the formula(14);Output:A weighted k-th hierarchical T-mesh with basis function that forma partition of unity.
4 Subdivision Scheme for PHT-Splines
Considering a knot vector{s0,s0,s1,s1,s2,s2,s3,s3},we insert a double knots′∈[s1,s2]in it.Then,we get the following relationship of B-splines before and afters′is inserted based on the B-spline knot insertion algorithm,
Based on the above formula,we derive the subdivision scheme for PHT-splines as follows.The support mesh of a basis vertexis supposed to beThe knot intervals of the support mesh are denoted byd0=si-si0,d1=si1-si,e0=tj-tj0,e1=tj1-tj.When elements are refined,new basis vertices are added.The new basis vertices lying in the interior of the refined elements are called face vertices,while the new basis vertices lying on the edge of the mesh are called edge vertices.The old basis vertices are called vertex points.Under the assumption that the level difference in an admissible hierarchical T-mesh is not greater than 1,the subdivision scheme of PHT-splines are deduced as follows.
· Vertex-points
If the refinement changes the support mesh associated withvki,the control points associated withare updated as follows:
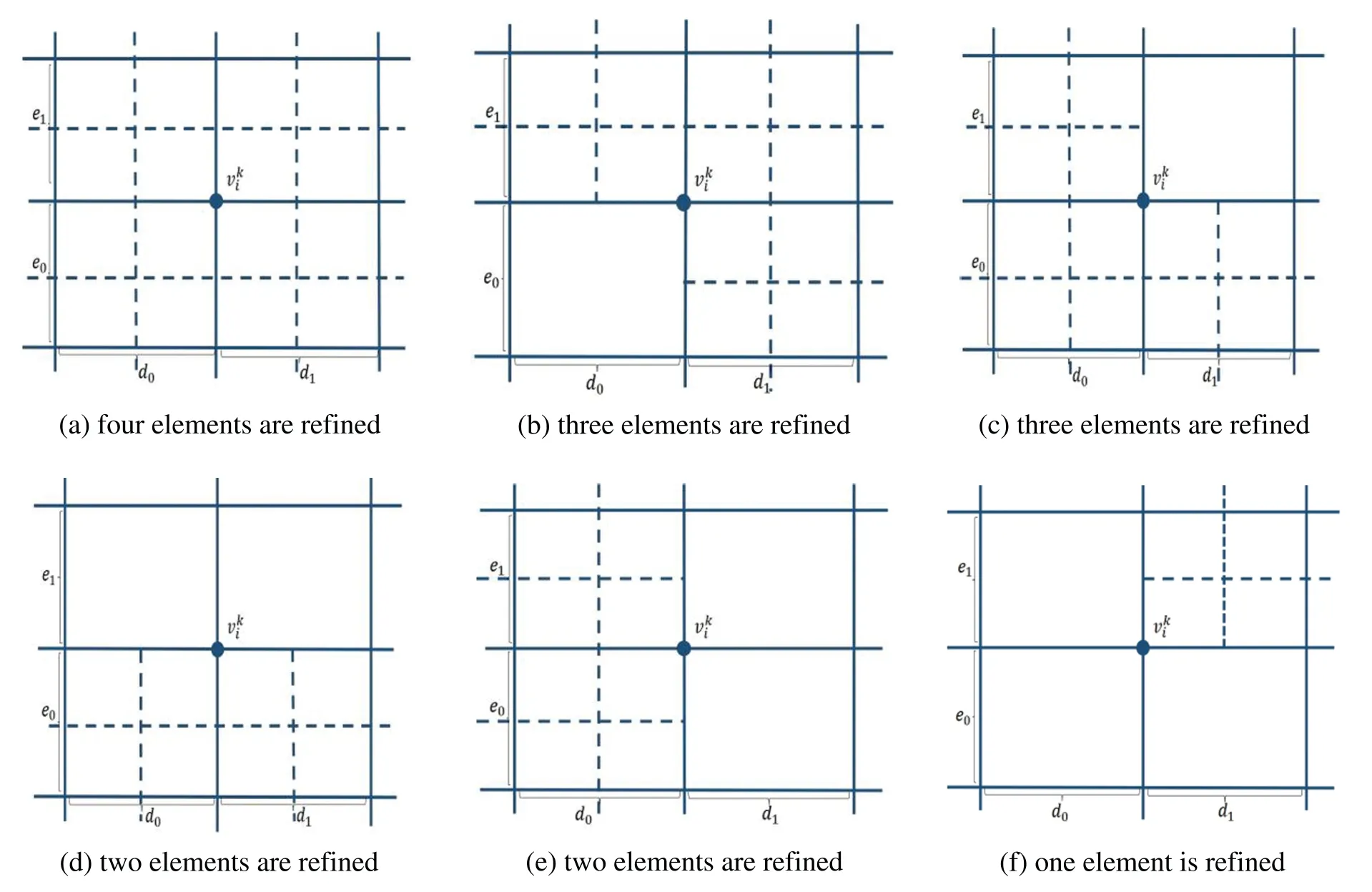
Figure 5 :Subdivision scheme of vertex points
· Edge-points
Supposevki+1is a edge point lying on the edge with endpointsand,referring to Fig.6.Since the level difference is assumed to be less than 2,andare two basis vertices.As shown in Fig.6a,the knot intervals forandare denoted by{d0,d1;e0,e1} and {d1,d2;e0,e1},respectively.We have the following edge-points updating formula.

Figure 6 :The subdivision scheme of edge points and face points
When the edge point lies on a vertical edge,as shown in Fig.6b,the update formula is similar to the above one,except thateisanddisare swapped.
· Face-points
Since we assume the level difference in the mesh is not greater than 1,so when an element is refined,the four corners are exactly basis vertices.Suppose the four basis vertices of the refined faceFare denoted byvi1,vi2,vi3,vi4.The knot intervals of these four basis vertices are denoted by{d0,d1,d2;e0,e1,e2},see Fig.6c for a reference.Here,we use the parameteraj=1 andaj=0 to indicate the support mesh ofvijis changed and unchanged,respectively.LetWe have the following formulas:
The weights satisfying (9) can be computed by this subdivision scheme.The control points(weights) at level 0 are all set to be 1.In the following,we take the hierarchical T-mesh shown in Fig.3a as an example to show how to use subdivision scheme to compute weights.
The weights are computed level by level.Fig.7 shows the refinement process.The weights of the basis functions on level 0 are set as[1,1,1,1],that is we setP04i+j=w04i+j=1 in the three formulas(20)–(22).Then we compute the weights associated with the basis vertices on level 1,see Fig.7b.The weights of the edge-pointare calculated by (21) withd0=0.25,d1=0.25,d2=0.25,e0=0.25,ande1=0.25.Consequently,we obtain=[1,1,1,1].The weights of other edge-points are calculated similarly and are all equal to[1,1,1,1].
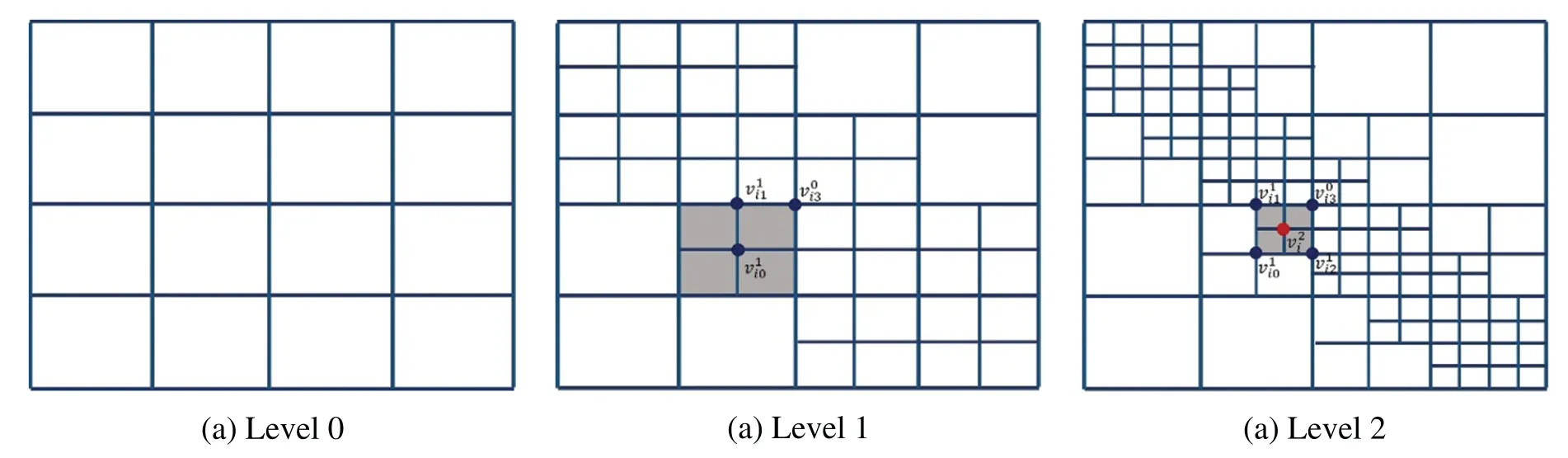
Figure 7 :The weights of each level of mesh in Fig.3a are calculated by the PHT-splines subdivision scheme
For the face point,the indicatorsajsfor the corners,andare all equal to 1,since their support meshes are changed,that isa1=a2=a3=1.Whilea0=0.The knot intervals for this case are set asd0=0.25,d1=0.25,d2=0.25,e0=0.25,e1=0.25,e2=0.25.The weights are thus computed based on(22)and are equal to
For the vertex pointv0i3,which is also a basis vertex of level 0,is updated based on (20),where[μ0,μ1,λ0,λ1]=[1,1,1,1],d0=d1=e0=e1=0.25 and=1,j=0,···,3.The weights of this vertex are all equal to 1.Notice here the support mesh ofis not changed,thus the weights are still equal to 1.
On level 2,the mesh is shown in Fig.7c,the face points and edge points of level 1 now become vertex points.For example,the vertices marked by blue circles are vertex points and updated based on (20).Since all the support meshes of these vertices are not changed,their weights are equal to the weights computed on level 1.For the update ofv1i1,v1i2,v0i3,because their weights are all[1,1,1,1],combined with sum of the coefficients of the update formula is 1,we easily obtain the updated weights of the three vertex-points are still[1,1,1,1].It is worth noting that if one of the basis functions of the three vertices has a weight other than 1,its weight will change after it is updated.
For the face pointv2i,the support of the basis vertexv1i0is not changed,so its weight is also set to 0 in the face-points formula,and the weights of the other three vertices are not changed.With their knot intervalsd0=0.125,d1=0.125,d2=0.125,e0=0.125,e1=0.125,e2=0.125,according to the formula of the face point,the weight of the new face pointis also
5 Numerical Experiments
The weighted basis functions not only avoid the decay phenomenon,but also form a partition of unity.The non-decay property reduces the condition number of the stiffness matrix,thus gives better numerical stability.This advantage has been explored in[2]and will not be repeated in this paper.The focus of this paper is to provide a way to efficiently calculate weights for non-decay basis functions so that non-decay PHT splines can be used in specific applications,such as topology optimization[14].
In this section,three typical hierarchical T-meshes demonstrate the validity of the proposed methods.We see that the weights on admissible hierarchical T-meshes are all positive.
The hierarchical T-meshes here are produced in the context of iso-geometric analysis.The Poisson equation is defined as
The exact solutionu(x,y)is chosen as three functions defined on[0,1]×[0,1].The first one is aC1–continuous function defined by
The other two are smooth functions with large gradients at some local regions,
andu3(x,y)=1000x6y6(1.0-x)2(1.0-y)2.The non-decay PHT-splines are adopted to adaptively solve the Poisson problem.Based on Algorithm 1 or the subdivision scheme,we compute the weights for the non-decay basis functions defined over the hierarchical T-meshes produced during the adaptive solving.
Fig.8a shows the plot ofu1(x,y).The diagonal elements are refined in each level to capture the feature of the solution.Figs.8b and 8c show the hierarchical T-meshes at levels 2 and 4,where the weights of the basis vertices are equal to ones,except for the basis vertices that are marked by colored circles.Notice that there are two basis functions with zero weights on level 4 (Fig.8c),because the underlying refined elements are isolated elements.This can be avoided by a further refinement of the adjacent elements.For this example,the level difference is less than 2.As the level increases,the weights of the old basis vertices are not changed.The weights of new basis vertices on each level have two kinds of values,except for the four ones at the corners.
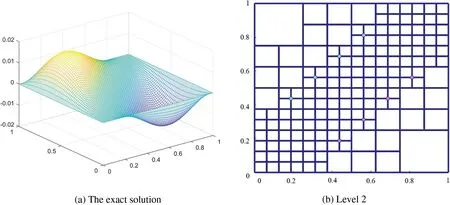
Figure 8 : (Continued)
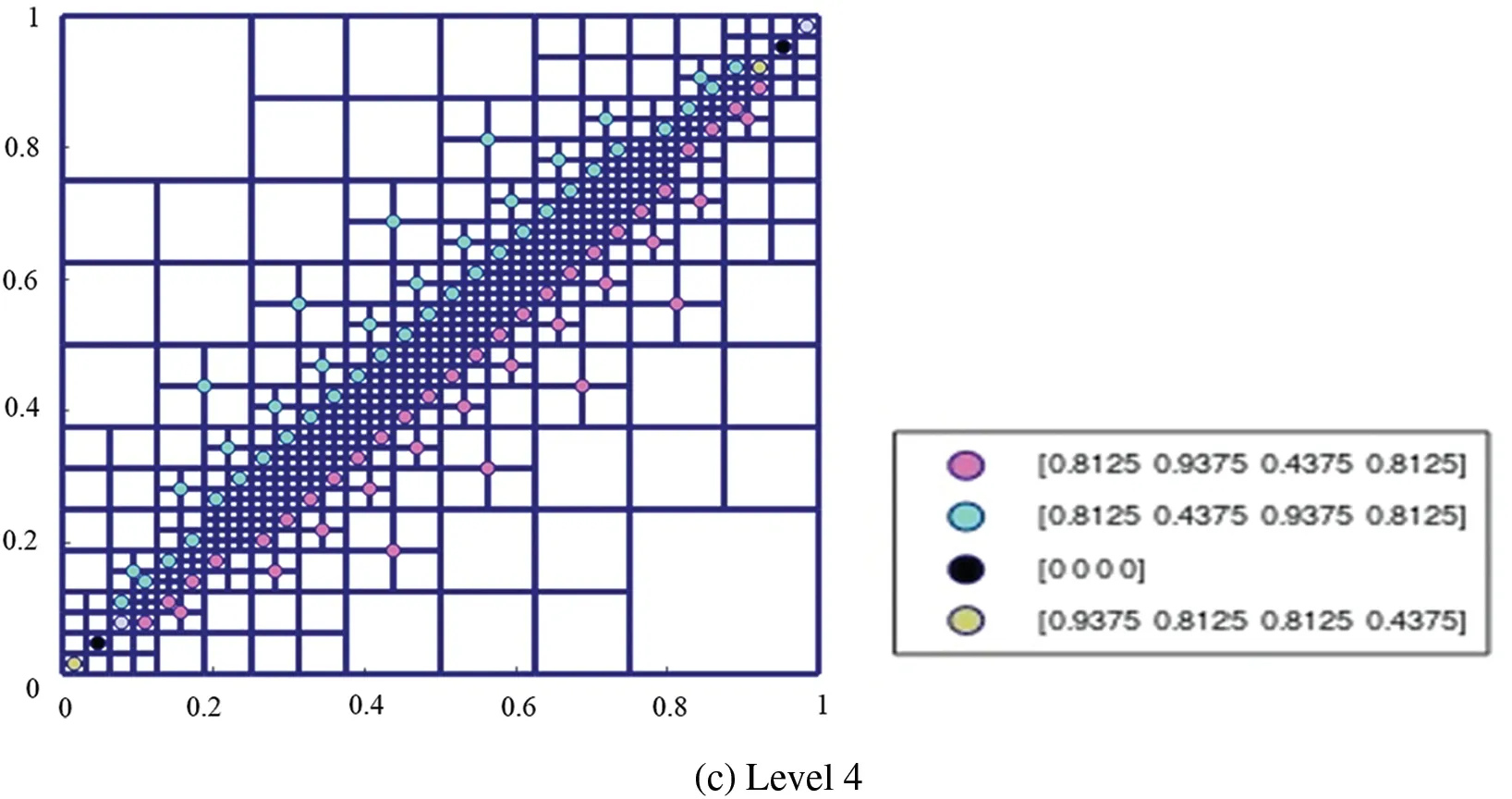
Figure 8 :The weights of the basis functions on the hierarchical T-mesh with diagonal elements refined
Fig.9a shows the plot ofu2(x,y).This function has very large gradients around the circle centered at(0.5,0.5)and decays very fast from the value 1 to the value-1.One can easily observe significant refinement around the large gradient area.Figs.9b and 9c show the hierarchical T-meshes at level 2 and 4,where the weights of the basis vertices are equal to ones,except for the basis vertices that are marked by colored circles.As the level increases,the weights of the old basis vertices are not changed.The weights of new basis vertices on each level have two kinds of vales.

Figure 9 : (Continued)
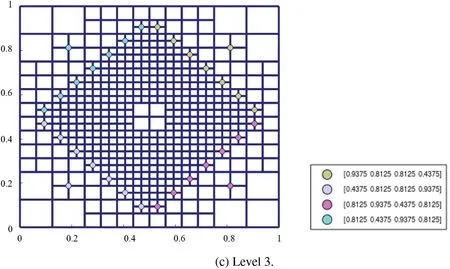
Figure 9 :The weights of the basis functions on the hierarchical T-mesh solved from u2(x,y)
Fig.10a shows the plot ofu3(x,y).For this example,the elements near the right-top corner are refined on each level to get hierarchical T-meshes that have greater level difference.Figs.10b–10d show the hierarchical T-meshes at level 1,2,3,where the weights of the basis vertices are equal to ones,except for the basis vertices that are marked by colored circles.As the level increases,the weights of the old basis vertices are changed.This can be seen from Fig.10e,where the weights of the basis vertexare changed as the refinement proceeds.Moreover,the closer to the left-down corner of the element,the smaller the weights of the face points,such as the weights of,and.This is caused by a greater level difference.
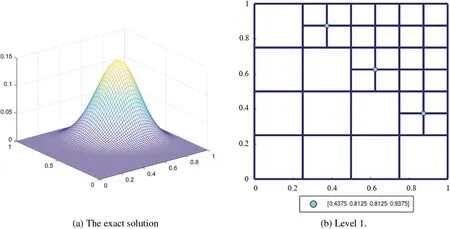
Figure 10 : (Continued)

Figure 10 : (Continued)
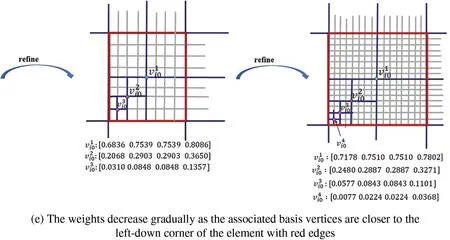
Figure 10 :The weights of the basis functions on the hierarchical T-mesh solved from u3(x,y).The level difference in these meshes is larger than 2
6 Conclusion
In this paper,we proposed two efficient ways of computing weights for the PHT-splines basis functions constructed in [2] such that the weighted basis functions form a partition of unity.The weights are expressed explicitly based on the geometric information of related basis functions or by the subdivision formula of HT-splines.Both algorithms can effectively compute weights.We proved that the weights are positive on the admissible hierarchical T-meshes.Three typical hierarchical T-meshes are demonstrated to verify the effectiveness of the proposed methods.
There are several problems worthy of further discussion.The first one is to derive the subdivision scheme in the case of arbitrary level differences.Another issue worthy of exploring is the application of PHT-splines defined by a weighted basis in topology optimization and isogeometric collocation.
Acknowledgement: The authors thank the reviewers for providing useful comments and suggestion.
Funding Statement: The work was supported by the NSF of China (No.11801393) and the Natural Science Foundation of Jiangsu Province,China(No.BK20180831).
Author Contributions: Falai Chen contributed to the conception of the study; Zhiguo Yong and Hongmei Kang contributed significantly to data analyses and manuscript writting; Zhiguo Yong performed the experiment.
Availability of Data and Materials:None.
Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.
 Computer Modeling In Engineering&Sciences2024年1期
Computer Modeling In Engineering&Sciences2024年1期
- Computer Modeling In Engineering&Sciences的其它文章
- Review of Recent Trends in the Hybridisation of Preprocessing-Based and Parameter Optimisation-Based Hybrid Models to Forecast Univariate Streamflow
- Blockchain-Enabled Cybersecurity Provision for Scalable Heterogeneous Network:A Comprehensive Survey
- Comprehensive Survey of the Landscape of Digital Twin Technologies and Their Diverse Applications
- Combining Deep Learning with Knowledge Graph for Design Knowledge Acquisition in Conceptual Product Design
- Meter-Scale Thin-Walled Structure with Lattice Infill for Fuel Tank Supporting Component of Satellite:Multiscale Design and Experimental Verification
- A Calculation Method of Double Strength Reduction for Layered Slope Based on the Reduction of Water Content Intensity
