Resource Allocation for IRS Assisted mmWave Wireless Powered Sensor Networks with User Cooperation

Yonghui Lin and Zhengyu Zhu

1Network Center,Zhengzhou University,Zhengzhou,450001,China

2School of Electrical and Information Engineering,Zhengzhou University,Zhengzhou,450001,China

ABSTRACT

In this paper,we investigate IRS-aided user cooperation (UC) scheme in millimeter wave (mmWave) wirelesspowered sensor networks (WPSN),where two single-antenna users are wireless powered in the wireless energy transfer(WET)phase first and then cooperatively transmit information to a hybrid access point(AP)in the wireless information transmission(WIT)phase,following which the IRS is deployed to enhance the system performance of the WET and WIT.We maximized the weighted sum-rate problem by jointly optimizing the transmit time slots,power allocations,and the phase shifts of the IRS.Due to the non-convexity of the original problem,a semidefinite programming relaxation-based approach is proposed to convert the formulated problem to a convex optimization framework,which can obtain the optimal global solution.Simulation results demonstrate that the weighted sum throughput of the proposed UC scheme outperforms the non-UC scheme whether equipped with IRS or not.

KEYWORDS

Intelligent reflecting surface; millimeter wave; wireless powered sensor networks; user cooperation; resource allocation

1 Introduction

The rapid expansion of the number of mobile devices has brought higher requirements for wireless applications,such as more extensive radio coverage,lower latency,higher data transmission rates and higher security,while the emergence of sixth-generation(6G)wireless technologies can perfectly meet such demands[1,2]describe the vision of future 6G communication and network architecture,which presents emerging technologies such as artificial intelligence,blockchain,quantum communications,integration of wireless information and energy transfer,integrated sensing and communication,intelligent reflecting surface and big data.Millimeter-wave (mmWave) communication has been widely regarded as a key technology of 6G,which owns ultra-wide bandwidth and high transfer speed advantages to meet the enormous capacity demand for 6G wireless communications [3,4].An exhaustive survey of mmWave wireless communications for future 6G networks is described in[5],where the latest channel measurement,modeling and multiple input multiple output (MIMO)transceiver designs are summarized.

Also,energy harvesting(EH),as one of the main techniques to power future 6G wireless networks,has been introduced as an efficient method that allows wireless devices to capture the energy from external environments [6,7].Radio frequency (RF) EH technique can enable an aggressive energy supply to the wireless devices (WDs) [8].As an promising and emerging EH technology,wireless power communication networks (WPCN) are of great interest as they have the potential to provide wireless power to energy-constrained devices such as the internet of things(IoT)and wireless sensor networks(WSN)to ensure their operation[9,10].Compared to the traditional battery-powered way,WPCN always provides more reliable and sustainable power replenishment.In WPCNs,the placement optimization of power and information access points is researched,where the WDs harvest the RF energy in the downlink and employ the harvested energy to transmit information to a base station in the uplink[11,12].

To improve the radio coverage and signal quality in a green way,an intelligent reflecting surface(IRS)has been proposed to reshape the signal propagation environment via passive reflecting arrays[13,14].The transmitted signal can be reflected the receiver through the IRS and constitutes the received signal together with the signal transmitted by the direct link[15].Thus,the reflected signal can be enhanced by properly adjusting the passive components of IRS[16,17].

Recently,some research on IRS-aided wireless powered sensor networks(WPSN)has been studied in [18–38].For maximizing the sum throughput in an IRS-aided WPCN,the closed-form solution for the phase shifts of the wireless information transfer has been derived,where a low complexity scheme was proposed to reduce the computational complexity of the semidefinite programming(SDP) scheme [18].Considering user cooperation (UC) in an IRS-assisted WPCN,the maximum throughput performance has been derived by jointly optimizing the power allocations,IRS phase shifts and the transmit time[19].By obtaining a closed-form solution by the Lagrange dual method and the Karush-Kuhn-Tucker conditions in an IRS-aided WPSN,Chu et al.[20]optimally designed the bandwidth allocation and the transmit time schedule.Li et al.[21]have maximized the minimum throughput performance for IRS-aided UC in a WPCN.To simultaneously improve the performance of uplink information transmission and downlink energy transfer,Lyu et al.[22]investigated a hybridrelaying self-sustainable IRS WPCN.Zhai et al.[23]has considered multicast transmissions in a gametheoretic way in an IRS-aided WPCN,where the closed-form optimal phase shifts have been derived.For a backscatter-assisted WPCN with an IRS,Ramezani et al.[24] have studied the maximization of total network throughput through a two-stage algorithm.In an IRS-assisted multiuser MISO WPCN,Zheng et al.[25] have maximized the weighted sum rate of all the energy-harvesting users by applying a block-structured optimization method.A novel dynamic IRS beamforming framework has been proposed to boost the sum throughput of an IRS-aided WPCN in[26].In order to strictly guarantee device quality-of-service(QoS)requirements,Zeng et al.[27]have considered the non-linear energy harvesting in an IRS WPCN.In a multi-user IRS WPCN,Cao et al.[28]have maximized the system throughput by optimizing jointly the energy beamforming,phase shift and time allocation.To maximize the sum throughput by applying the Lagrange dual method,a closed-form solution has been derived for the optimal power allocation,transmission time slots and phase shift for IRS-aided wireless powered IoT system[29].

To tackle the issue of the uplink transmission of WDs in WPCNs depending on the harvested energy from the downlink,Wang et al.[30]proposed an energy efficient optimization method in IRSassisted WPCN by the variable-substitution approach.In order to ensure fairness,Zeng et al.[31]studied a weighted sum throughput maximization in an active IRS-aided WPCN by applying three beamforming setups.Using the semidefinite relaxation method,Lyu et al.[32]considered a sum rate maximization for the IRS-aided WPCN by jointly iteratively optimizing the time scheduling and the phase shift.In the presence of eavesdropper,Cao et al.[33]proposed three secure modes in physical layer security of an IRS-aided WPC system,where asymptotic ergodic secrecy capacity is analyzed and closed-form expression is obtained.A new transmission policy for an IRS-assisted WPSN with certain phase shifts is proposed by maximizing the system sum throughput in[34],in which IRS can collect energy to achieve its self-sustainability.In a MISO transmission form,a practical IRS can work in EH with a power budget constraint,and then utilize the harvesting energy to sustain its operations in the signal reflecting phase [35].Considering cognitive loT devices,two transmission policies are studied with a successive interference cancellation technique [36],where the interaction between primary and secondary networks is characterized by a Stackelberg game strategy.An IRSaided wireless powered over-the-air computation Internet-of-Things network is investigated to propose a joint design of energy beamforming at the access point,downlink and uplink phase-shift matrices,as well as transmit power,in order to minimize the mean-squared error[37].With the aid of an IRS,in wireless powered non-orthogonal multiple access(NOMA)IoT networks,by jointly optimizing the time allocation and phase shift matrices of wireless energy transfer and wireless information transfer,a novel resource allocation approach is proposed by maximizing the sum throughput in[38].

Integrating the IRS technology with sensor networks can achieve a self-sustaining system,specifically by embedding the IRS to the existing WPSN to reflect energy and information signals to improve the wireless energy transfer(WET)and wireless information transfer(WIT)capabilities of the WPSN.Also,to achieve a better performance with the IRS-assisted scheme,we consider a mmWave WPSN UC system in the uplink,i.e.,one user not only completes his own signal transmission task,but also assists other users in completing signal transmission as a relay.Different from the existing works on the IRS-aided WPCN system,the research of transmission strategies in an IRS-assisted WPSN systems with UC in the mmWave band has not been made yet.We summarize our contributions as follows:

1.First,an IRS has been used to improve the performance of the WPSN system with UC in the mmWave channel,where two single-antenna wireless devices can harvest energy radiated by a hybrid access point (AP) to support the separate information transmission to the AP.Here,the IRS play a role in promoting the system performance of the downlink wireless energy harvesting and the uplink wireless information transmission by energy and information reflection for the IRS,respectively.

2.Second,it aims to maximize the weighted sum-rate through jointly optimizing the power,the time slots allocation and the IRS phase shift of the WET and WIT is used to evaluate the performance of the proposed system model.Since the original problem is non-convex with respect to the coupled variables of the power and the IRS phase shift,it is hard to solve directly.

3.Finally,to deal with the non-convexity of the original formulated problem,the semidefinite programming relaxation (SDR) technique is applied to convert the weighted sum-rate maximization(WSRM)problem to a convex optimization framework,which can obtain the global optimal solution.Simulation results proved that the IRS and the UC can improve the system performance compared with the two latest benchmarks.

The rest of the paper is organized as follows.Section 2 introduces the system model of an IRSaided WPSN system with mmWave channel.In Section 3,a weighted throughput maximization problem with user cooperation is discussed carefully,and we develop a SDR-based algorithm to solve the original problem.In Section 4,our simulation results demonstrate the effectiveness of the proposed SDR algorithm.In Section 5,the paper is summarized.

2 System Model

As shown in Fig.1,we investigate an IRS-aided mmWave WPSN system,which contains a singleantenna AP and two single-antenna wireless users(WUs).Due to the constrained energy of devices,the wireless communication links(WCLs)of harvesting energy in the UL are established between AP and WUs.In the downlink(DL),information signals also can be transmitted through these links.Without loss of generality,we assume that WU2is used as a relay between WU1and AP in the meantime.An IRS withNdynamically adjustable elements is equipped to strengthen WCLs,and only one-time signal reflection by the IRS is considered owing to the path loss.The phase shift matrix of IRS is defined asθ=[θ1,...,θN]andΘ=diag(ejθ1,...,ejθn,...,ejθN).Denote g ∈CN×1and gRk∈CN×1as the mmWave channel matrix for the channel of AP to IRS,IRS to WUk,wherek=1,2.hk,h21are the channel between AP and WUk,WU1and WU2,k=1,2,and all channel gains areg=‖g‖2,gRk=‖‖gRk

‖‖2,ζk=|hk|2,ζ21=|h21|2,respectively.Also,we assume that all channels between different transceiver and receiver are independent and identically distributed complex Gaussian distribution ofCNwhereκ2depending on the path loss.In this paper,our research focuses on finding a suitable optimal algorithm for IRS phase shifting,the power,the time slots allocation and deriving an upper bound on the weighted sum-rate performance of the system model under study.Therefore,we assume that CSI is perfect and we can get the CSI acquisition method under the IRS assisted WPSN system.In the paper,we further elaborate on the reasons for assuming a perfect CSI and how to obtain it.

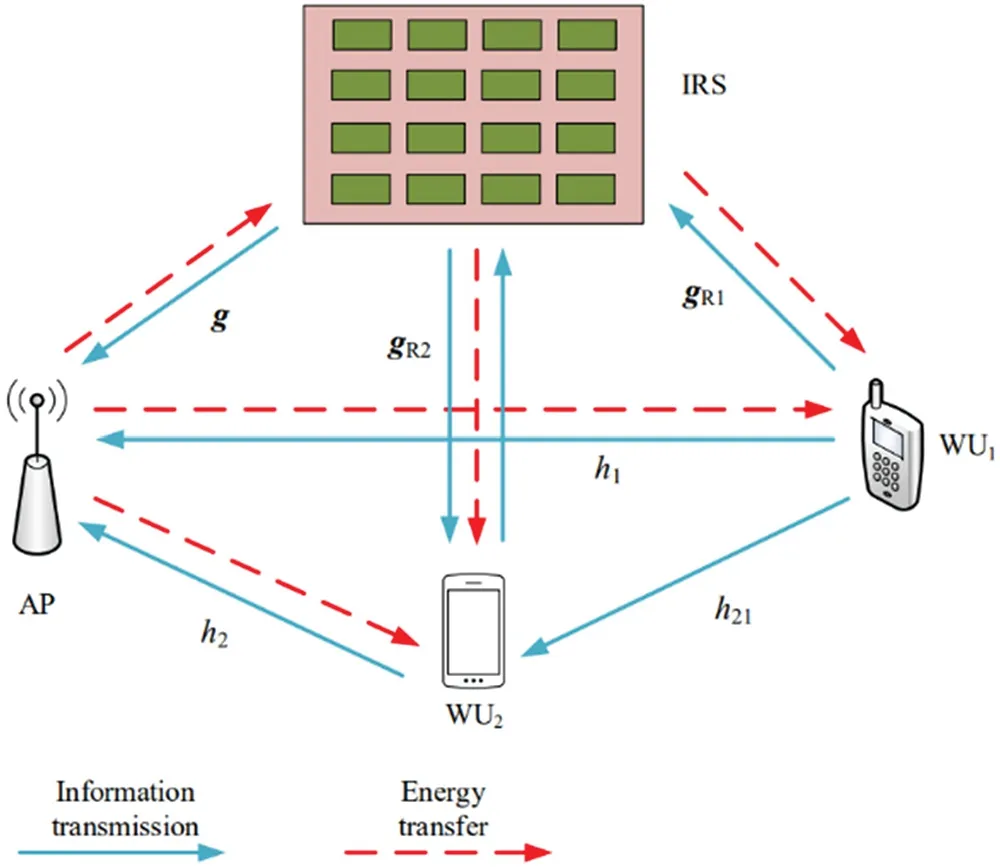
Figure 1 :The IRS-aided mmWave WPSN system model

For the mmWave channel of AP to IRS,IRS to WUk,k=1,2,the antenna response can be written as

whereφandθrepresent the incident signal’s angles of azimuth and elevation,λanddare the wavelength and antenna spacing,respectively.Therefore,the mmWave channel matrix written as

whereNtandNrrepresent the number of transmitting and receiving antennas,andLdenotes the total number of paths,including one LOS direct path and(L-1)NLOS paths.ρis the path loss andρ=δd-γ,whereδ,d,andγare a constant,the geographical distance and the path-loss exponent,respectively.The WET and WIT processes are considered within the time periodTthat usually be assumedT=1s.In the WET,the AP charges WUs during time periodτ0T(τ0∈(0,1])in the DL.At the same time,part of the energy transmitted by the AP will be reflected to the WUs through the IRS,and the received energy contains two parts,i.e.,AP →WUk,AP →IRS →WUk,k=1,2.Thus,the received information signals at WUs can be expressed as

wherep0is the transmit power of the AP,and theΘ1=denotes the coefficient matrix of reflected energy by IRS.Defineθ1,ndenotes the phase shift of the IRS and=1,n∈[1,N],xis the energy signals satisfyingx～CN(0,1),andn(t)～at WUk,k=1,2.Hence,the harvested energy at WUkwas donated as

whereηrepresents the efficiency of energy harvesting during the WET phase.

The time of the WIT phase is(1-τ0)T,where WUs transmit the information to the AP and the IRS by using the harvested energy.In the WIT scenario,we assume that WU1and WU2can transmit information signals directly to the AP simultaneously,and WU2can act as a passive relay,reflecting some information signals from WU1to AP.As shown in Fig.2,to further express this process,the time allocation of the WIT phase is divided into three sub-phases:

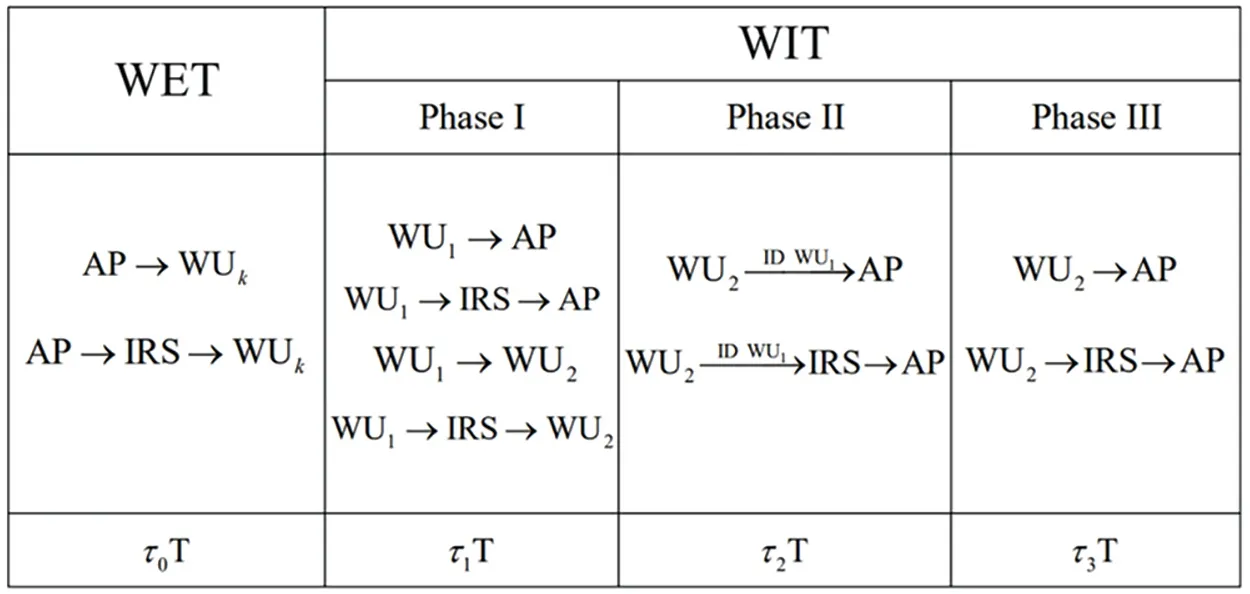
Figure 2 :System time allocation of WET and WIT

1.In the first sub-phase,i.e.,τ1T,WU1transmits the information signal to the AP and WU2using the harvested energy(i.e.,WU1→AP,WU1→WU2).Also,the signal of WU1is reflected to the AP and WU2via the IRS(i.e.,WU1→IRS →AP,WU1→IRS →WU2);

2.In the second sub-phase,i.e.,τ2T,WU2first decodes WU1’s information signal and then forwards it to the AP and the

3.In the third sub-phase,i.e.,τ3T,WU2transmits the information signal to the AP and the IRS(i.e.,WU2→AP,WU2→IRS →AP).

In the first sub-phase,the harvested energy obtained in WET is used in WET and the transmit power of WU1is

Then,the information signal received at AP and WU2are expressed respectively as

wheres1is the information signal from WU1withE[|s1|2]=1,Θ2=denotes the IRS’s reflection coefficient matrix with=1,n∈[1,N],nAPandn2denote the received noise power of the AP and WU2with varianceandσ22,respectively.The achievable rates in this phase are expressed as

In the second sub-phase,the signal received at AP given by

wherep(2)2is the transmit power of WU2within the subphase,Θ3=denotes the reflection coefficient matrix withrepresents the transmit information symbol of WU2associated with WU1’s information.Then,the achievable direct rates from WU2to the AP are expressed as

The information signals transmitted from WU1to AP have four different paths,where the signal of AP in the first path is the direct link from WU1(i.e.,WU1→AP),the signal of AP in the second path is secondarily transmitted by WU2with proposed UC scheme(i.e.,WU2AP),the signal of AP in the third path is the direct link from WU1via IRS (i.e.,WU1→IRS →AP),and the signal in the fourth path is secondarily transmitted by WU2with UC scheme via IRS to AP(i.e.,WU2IRS →AP).Therefore,the achievable rate from WU1to AP is given by

where

In the third sub-phase,the information signal received at AP is written as

wherep(3)2denotes the transmit power of WU2in this sub-phase and the achievable rate from WU2to AP is expressed as

The energy obtained by WU2inτ0Ttime period should be greater than that consumed in the latter two sub-phases,so that the later work can be completed normally.So,there is

According to the above transmission process,the time periodτ1,τ1,τ2,andτ3in this WPSN need to satisfy the following time constraints written as

3 Weighted Throughput Maximization with User Cooperation

Using the derivation and definition from the previous step,a WSRM problem is formulated based on a UC scheme and then solved by jointly optimizing the phase shift matrices,time allocation,and power allocation.First,the WSRM problem is given by

whereαand 1-αare preference constants ofRAP,1andRAP,2,respectively.Problem (P1) is not convex due to the objective function and the constant modulus constraint in the phase shift matricesΘ1,Θ2,Θ3,which leads to the time allocationτ={τ0,τ1,τ2,τ3},and power allocation p=cannot be solved efficiently.

For the non-convexity of problem(P1),we can introduce some transformation forms for the phase shift matrices to tackle it.So,we have

Then,introducing auxiliary variablesμ2=τ2p(22)andμ3=τ3p(23),another form ofandRAP,2can be expressed as

Accordingly,by introducing another auxiliary variable,RAP,1can be recast as

Due to the rank-one constraint causing the problem to be non-convex,so we use the SDR approach to remove this constraint,then(P1)can be reformulated as

Here,the problem(34)is now a convex optimization problem.Thus,the global optimal solution can be obtained by CVX in Matlab[40,41],which is denoted asThe computational complexity of the SDP relaxation scheme iswheren=

Combined with the above derivation,we can further obtain the optimal values as

The rank-one solution may be obtained from the relaxed WSRM (P3).So we employ the eigenvalue decomposition for Aopt1to obtain thewhereΨ∈C(N+1)×(N+1)represents a unitary matrix,T ∈C(N+1)×(N+1)represents a diagonal matrix.We can obtainwhereνis complex circularly symmetric Gaussian variables withν～CN(0,IN+1).Then,the optimal aopt1is identified byθ1,i=

4 Simulation Results

The simulation results are presented to evaluate the performance of the user cooperation scheme in IRS-aided mmWave WPSN.The illustration of the system is shown in Fig.3.We assume that AP and WUkare on the same level,and the distance between the IRS and this horizontal line is 4 meters and the distance between AP and IRS isd2=5 m.Finally,the settings of other parameters are shown in Table 1.In the specific simulation,some benchmark methods are introduced as the simulation comparison to show the superiority of the proposed method:

Table 1 : Simulation parameters

1.IRS+UC:IRS helps WUs to harvest energy through reflection in the WET phase.In the WIT phase,IRS reflects signals from WUs to AP,and WU2can receive and secondary transmit signals from WU1to AP as a relay in the UC scheme.

2.Non IRS+UC:Following[12],WUs only harvest energy through the direct link from AP in the WET phase and the UC scheme is considered in the WIT.

3.IRS+Non UC:Following[26],Only IRS works and UC scheme is canceled.

4.Non IRS+Non UC:There are no IRS and UC schemes in the system.

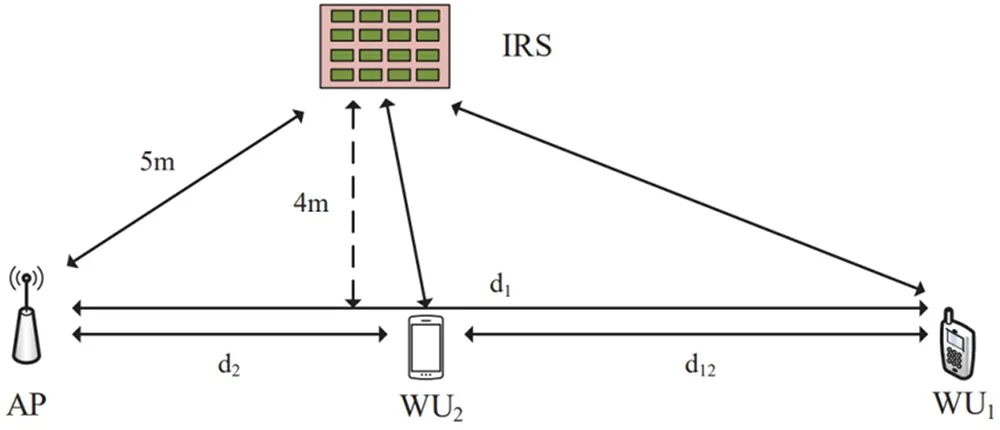
Figure 3 :Simulation model

We first evaluate the sum throughputvs.the distanced1between the AP and WU1in Fig.4.Whend1changes from 5 to 10 m,the channel between AP and WU1will be influenced,which will affect the sum throughput.In this simulation,p0=30 dBm,N=25.Whether equipped with IRS or not,sum throughput using UC outperform the sum throughput without the UC scheme,which shows that the UC scheme can effectively improve sum throughput in IRS-aided mmWave WPSN.Whend1=10 m,the gap of sum throughput between “IRS + UC” and “IRS + Non UC” or “Non IRS + UC” and “Non IRS+Non UC” become smaller compared withd1=5 m.This is because the efficiency of the UC scheme will be affected when the distance between wireless users is large.At the same time,it can be known that the improvement of sum throughput by only using the UC scheme is greater than that only equipping with IRS.

In order to observe the sum throughput improvement with increasingp0,we second compare the performance of some different schemes whenp0increases from 30 to 40 dBm in Fig.5.We setd1=8 m,N=25 here.It can be seen from the figure that the sum throughput of four schemes increases with the increasingp0,but the “IRS+UC” scheme outperforms that of other schemes.We can realize that the UC scheme can improve sum throughput significantly even if the WUs get less energy in WEL.This also provides a feasible way to make up for the lack of energy by introducing the UC scheme into WPSN.

Finally,the impact of the elements numberNof IRS on sum throughput is shown in Fig.6.With the increasingN,the sum throughput obtained by schemes with IRS is gradually increased due to the array gain and the sum throughput of schemes without IRS not changing.When aboutN＜50,“IRS+ UC” and “Non IRS + UC” outperforms “IRS + Non UC” and “Non IRS + Non UC”.Then “IRS+Non UC” is greater than “Non IRS+UC” asNcontinues to grow,and this is because the performance gain of increasingNto that only equipping with IRS is greater than that only using UC scheme in mmWave WPSN.

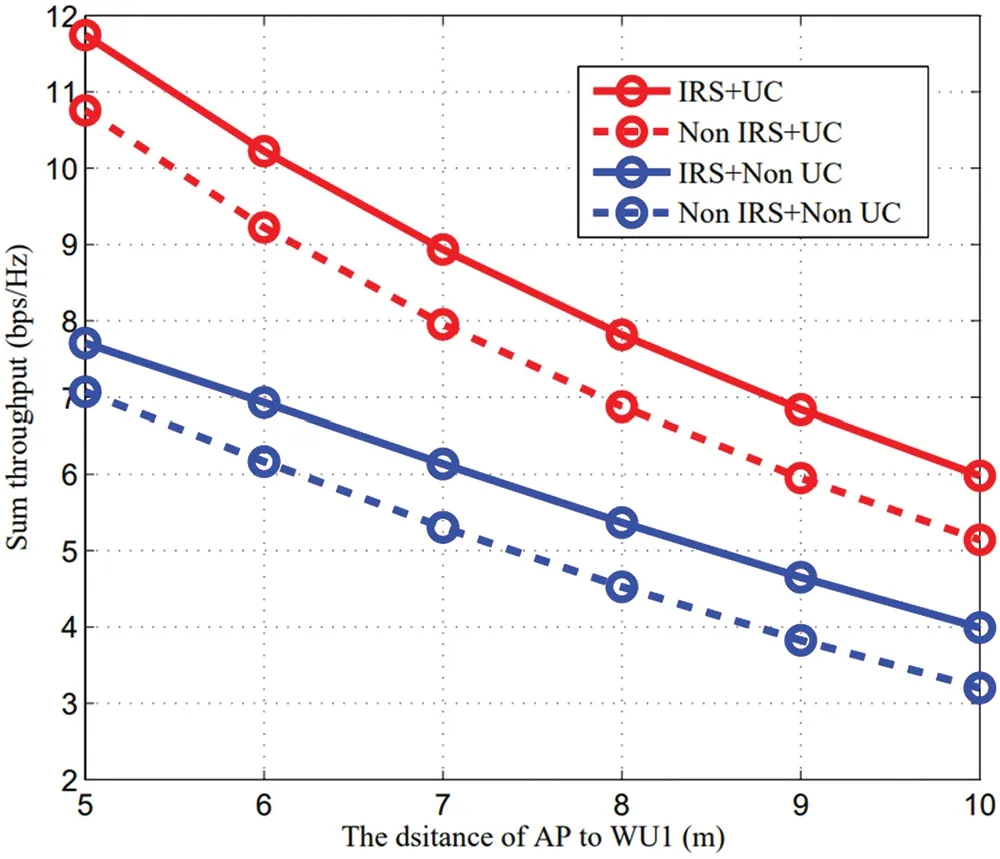
Figure 4 :Sum throughput vs.d1

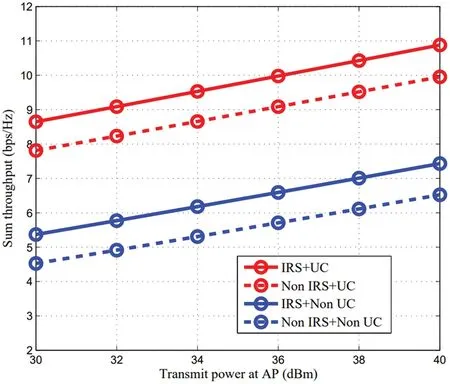
Figure 5 :Sum throughput vs.P0

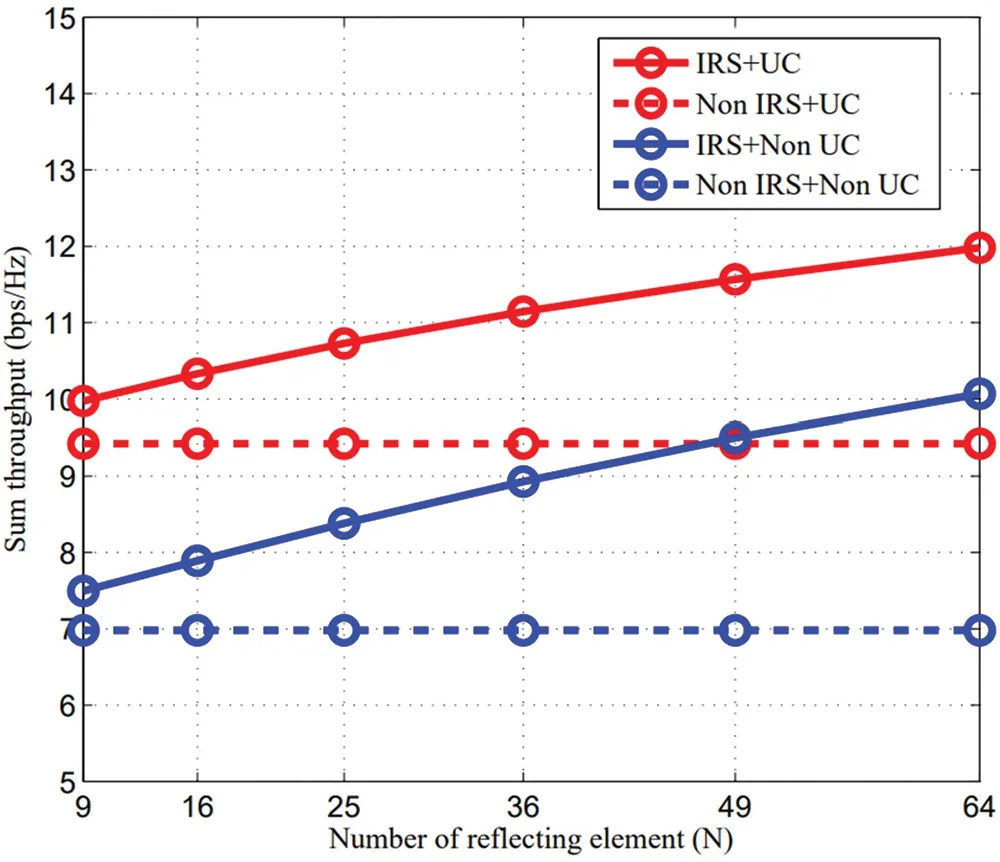
Figure 6 :Sum throughput vs.N

5 Conclusion

In this paper,we proposed a UC scheme for IRS-aided mmWave WPSN.The WSRM problem is formulated to maximize the weighted sum throughout by jointly optimizing the phase shift matrix,time slots,and power allocation.Some efficient variable substitutions and SDP relaxation are introduced to convert the original non-convex problem into a convex problem that is easy to tackle.Finally,numerical results confirm that the weighted sum throughput of our proposed UC scheme is greater than that of non UC whether equipped with IRS or not.

Acknowledgement: This work was supported in part by the open research fund of National Mobile Communications Research Laboratory,Southeast University (No.2023D11),in part by Sponsored by Program for Science & Technology Innovation Talents in Universities of Henan Province(23HASTIT019),in part by Natural Science Foundation of Henan Province(232300421097),in part by the Project funded by China Postdoctoral Science Foundation (2023T160596,2020M682345),in part by the Henan Postdoctoral Foundation(202001015).

Funding Statement:This work was supported in part by the open research fund of National Mobile Communications Research Laboratory,Southeast University (No.2023D11),in part by Sponsored by program for Science & Technology Innovation Talents in Universities of Henan Province(23HASTIT019),in part by Natural Science Foundation of Henan Province (20232300421097),in part by the project funded by China Postdoctoral Science Foundation(2020M682345),in part by the Henan Postdoctoral Foundation(202001015).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yonghui Lin,Zhengyu Zhu; data collection: Yonghui Lin,Zhengyu Zhu; analysis and interpretation of results:Yonghui Lin,Zhengyu Zhu;draft manuscript preparation:Yonghui Lin.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:This statement should make clear how readers can access the data used in the study and explain why any unavailable data cannot be released.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.