A Large-Scale Group Decision Making Model Based on Trust Relationship and Social Network Updating

Rongrong Ren,Luyang Su,Xinyu Meng,Jianfang Wang and Meng Zhao,4,★

1School of Business Administration,Northeastern University,Shenyang,110819,China

2School of Management,Northeastern University at Qinhuangdao,Qinhuangdao,066004,China

3School of Modern Logistics,Shanxi Vocational University of Engineering Science and Technology,Taiyuan,030031,China

4Business School,Sichuan University,Chengdu,610064,China

ABSTRACT

With the development of big data and social computing,large-scale group decision making(LGDM)is now merging with social networks.Using social network analysis(SNA),this study proposes an LGDM consensus model that considers the trust relationship among decision makers(DMs).In the process of consensus measurement:the social network is constructed according to the social relationship among DMs,and the Louvain method is introduced to classify social networks to form subgroups.In this study,the weights of each decision maker and each subgroup are computed by comprehensive network weights and trust weights.In the process of consensus improvement:A feedback mechanism with four identification and two direction rules is designed to guide the consensus of the improvement process.Based on the trust relationship among DMs,the preferences are modified,and the corresponding social network is updated to accelerate the consensus.Compared with the previous research,the proposed model not only allows the subgroups to be reconstructed and updated during the adjustment process,but also improves the accuracy of the adjustment by the feedback mechanism.Finally,an example analysis is conducted to verify the effectiveness and flexibility of the proposed method.Moreover,compared with previous studies,the superiority of the proposed method in solving the LGDM problem is highlighted.

KEYWORDS

Large-scale group decision making; social network updating; trust relationship; group consensus; feedback mechanism

1 Introduction

Due to the increasing complexity of the social and economic environment,it is increasingly difficult to rely on a single decision maker (DM) to make effective decisions.Therefore,many organizations use multiple members in the decision-making process,which is called group decision making (GDM).GDM is a participatory process,which selects the best solution from alternatives by considering the personal opinions of multiple experts [1].However,with the rapid development of technology and society[2],the group sizes have gradually become larger and more complex[3,4].Generally,a group with more than 20 members is defined as a large-scale group.

In the background of LGDM,decision makers(DMs)may have diverse opinions because of the different knowledge and experience.Therefore,how to help DMs reach consensus becomes a key issue.In order to deal with the complexity and uncertainty of the LGDM problem,this study starts from the following aspects:the dimensional reduction of large-scale DMs[5],the consensus measure and the improving method.

The dimensional reduction of large-scale DMs.There are two main directions for reducing the size of large-scale DMs.The one is based on the department or field in which the DM belongs.For example,Liu et al.[6] classified the DMs according to the DMs’school,and determined the percentage distribution on evaluations of each group concerning each alternative.The characteristics of this direction are simple and convenient.But in the real process,judgment information given by the same type of DMs is not necessarily the same.Therefore,the clustering method based on the evaluation value or preference value of DM is used to reduce the dimension of large-scale DMs.For example,Wu et al.[7] used the k-means method to cluster a large amount of hesitant fuzzy preference information and improved consensus level based on three-level consensus measures and a local feedback strategy.Yang et al.[8] investigated the additive consistency of the intuitionistic fuzzy preference relations in group decision making using T-normalized intuitionistic fuzzy priority vectors.In the above studies,DMs are considered as independent individuals.However,there are social relationships among DMs,especially the trust relationship which is clearly existed and important in reality.

Social networking applications generate a huge amount of data daily.Meanwhile,social networks(SNs) have become a growing field of research due to the heterogeneity of data and structures,as well as their size and dynamics [9].Some studies have proven the advantages of social networking,such as social network-based recommendation systems[10–12],online review websites incorporating the social-networking function [3,13],collaborative networks in the con53text of publications and citations[14,15],preventing the spread of rumors and misinformation by identifying influencers[16–19].Information on SNs can not only enrich and improve the DMs’preference information,promote and accelerate consensus reaching process,but more importantly,reduce the dimension of large-scale DMs.Trust is a special case in social relations,and some studies have also analyzed the impact of trust relations on clustering [20,21].Therefore,in the framework of social network-group decision making (SN-GDM),it is novel and feasible to use trust relationship as a reliable source of member weight information.However,most existing studies only consider the trust relationship between nodes without considering the trust degree of different nodes;they also ignore the generation process of relationship network,and cannot automatically cluster in the process of dimension reduction.In addition,previous studies that applied SNA to large group networks did not consider network construction and update based on DMs feedback,except for the trust relationship among DMs.

The consensus measure and improving method.On the one hand,an interesting issue within the group decision theory is the consensus measure,and the key of the problem is how to determine the DMs’weight and subgroup weight in the process of decision matrix aggregation.In GDM,the decision matrix is generally aggregated through subjective or objective weighting to perform consensus measures.In particular,expert weights may be adjusted during the consensus reaching process.Pang et al.[22] developed an extended TOPSIS method and aggregation-based method for multi-attribute group decision making(MAGDM)with probabilistic linguistic information in the case where the attribute weights are unknown and partially known.Wu et al.[23]used trust score values to assign importance weights to experts.For LGDM,the weight of individual DMs and the weight of each subgroup need to be determined after clustering.For example,Wu et al.[5] determined the expert weight through the centrality of the network.Wu et al.[7] determined the subgroup weight based on the number of experts in the subgroup.Shi et al.[24]used a uniform aggregation operator to update the weights in the consensus reaching process(CRP).According to the above research,group consensus can be improved quickly by adjusting the weight of DMs and subgroups in the CRP.This is also in line with reality.The influence of some DMs may increase in the process of DM interactions,resulting in the corresponding changes in weights.Although the above studies involve weight changes in the CRP,the trust relationship between DMs is rarely considered.Generally speaking,DM with strong trust relationships has a greater influence.In the process of interaction,DMs with strong trust relationships will affect the preferences of DMs with weaker trust relationships.

On the other hand,scholars have proposed consensus improvement methods for LGDM consensus problems[7,25–28],which are mainly divided into automatic methods[29,30]and interactive methods[31,32].The automatic feedback mechanism saves time because it does not require additional expert interaction to carry out the consensus-improving process.For example,Zhang et al.[33]proposed an automatic feedback mechanism for group decision making based on the distribution linguistic preference relations.Perez et al.[34]overcame the problem of the moderator,giving a way to use an automatic system to compute and send customized advice to the experts if there is not enough consensus.The interactive feedback mechanism requires expert interaction,which takes more time but the results obtained are more accurate.For example,for the cooperative and noncooperative behaviors of experts,Quesada et al.[35] introduced a method to deal with noncooperative behaviors,which used an informal weighted scheme to assign weights to experts.Gou et al.[36] built a consensusreaching model of noncooperative behavior and deal with noncooperative behavior and preference information.In addition,Gou et al.[37]used multi-stage interactive consensus reaching algorithms to deal with multi-expert decision making problems with language preference ordering.For the dynamic adjustment process of consensus reaching,in [1],a non-linear programming model was constructed to dynamically adjust the experts’weights in consensus reaching process.Wu et al.[7] proposed an LGDM consensus model which allowed clusters change.And as the clusters changed in every interactive consensus round,the consensus process evolution could be captured.Besides,some studies have also considered social networks.For example,in[5],after the feedback mechanism is executed,clustering and consensus measures are performed again,the process of consensus improvement is not involved.However,the social network was applied in [5] which applied IT2-TOPSIS to obtain the optimal solution directly.In the above research on consensus improving,social networks,trust networks,interaction rules,and the update and optimization of the entire network structure in the adjustment process are rarely considered.However,in the actual adjustment process,it is necessary to consider the acceptability of information and let DMs with higher trust interact with each other.The interaction process will inevitably lead to changes in the trust relationship among members of the large group.Therefore,it is necessary to consider the update of the trust network in the process of consensus improvement.

Trust relationships have been applied in various fields and have brought great benefits to various industries.In the business field,marketing methods such as fan economy,word-of-mouth bonus,media marketing,onlookers,and participation experience have brought unexpected dividends to enterprises in the era of mobile internet.Among them,the cultivation of trust relationships is the key,and trust is the core of this emotional marketing.Similarly,in academia,the citation relationship between different scholars also reflects the trust between each other,which may further lead to collaboration relationships.In politics,the trust relationship between voters will also greatly affect the election results.Therefore,it is necessary to consider the trust relationship and trust network in LGDM.In addition,considering trust networks based on group classification of decision makers can better reflect the trust relationship,and the trust degree and the degree of information difference can be better reflected in the group consensus.Considering trust relationships can achieve more effective interactions in the feedback adjustment process.

In view of the necessity of trust in decision making,this study will take the trust relationship through the entire decision-making process,from social network construction and clustering to weight determination and consensus measurement,as well as consensus reaching process and network updating.In comparison with the previous consensus model,the consensus model proposed in this study has some distinctive features:

First,in previous studies,the SNA was typically used to simply represent the relationship of DMs.It did not really combine the actual social activities of the DMs.Considering the social trust relationships between DMs for the LGDM,this study builds a social network between DMs and uses the Louvain method to detect community based on the trust relationship.

Second,in the process of determining the weight of individual DMs and the weight of each subgroup,the trust weight and the network weight are fully considered.Compared with weights based on network degree centrality or subgroup size,it is more convincing to assign weights based on trust relationships and to make corresponding weight changes in the feedback adjustment process.In addition,the weight for individual DMs and the weight of each subgroup will update accordingly in the consensus reaching process.

Third,the proposed model allows for changes in the trust network.Individuals are able to modify their preferences in the reaching consensus process,so the trust relationship will change,which will make the number of subgroups and members of each subgroup likely to change.In addition,the consensus rules and adjustment rules proposed in the model are simple and can be used to guide modifications.

The remainder of this study is organized as follows.Section 2 introduces related concepts,such as social relationship and social impact analysis,possibility distribution based on hesitant fuzzy elements,and probability distribution based on fuzzy preference relations.Section 3 presents the proposed SNAbased LGDM method.In Section 4,an illustrative example is provided to show the applicability of the proposed method.Section 5 compares and analyzes the similarities and differences between the proposed method and the other methods in detail,cutting from the three perspectives of trust relationship,social network and subgroup classification method.Finally,Section 6 concludes this paper with future perspectives.

2 Preliminaries

2.1 Measurement of Trust among DMs

In this study,we distinguish senders and receivers of social ties,which means the DM’s online network is directed.The in-degree of a DM refers to the social ties that the DM has received from other DMs.The out-degree indicates the social ties that the DM has sent to other DMs [38].The definitions of in-degree centrality and out-degree centrality are described as follows.

Definition 1[39]:LetG=(E,L)be a directed graph,E={e1,e2,...,em}be the set of nodes andbe the set of directed edge between pairs of nodes.

(1)The number of edges originating from nodeeris called the out-degree centrality index of the nodeer.

whered+(er) represents the out-degree centrality of the DMer.If there is a link fromertoet,thena(er,et)=1;Otherwisea(er,et)=0.

(2)The number of edges terminating from the nodeeris called the in-degree centrality index of the nodeer.

whered-(er) represents the in-degree centrality of the DMer.If there is a link fromettoer,thena(et,er)=1;otherwisea(et,er)=0.

The relationship strength between members shows the level of trust between those members[38].Within online social networks,members can declare friendship with one another by establishing social.If two DMs have more common social connections in an online social network,we can conclude that they have deeper social ties.This study uses degree centrality to calculate social connection strength betweenerandeh[22]:

wherenrhis the number of common social connections betweenerandeh,which is measured by the number of common edges oferandeh.The more common social connections oferandehare the stronger the social tie betweenerandehis.

Social interaction strength is a combination of time length,emotional intensity,intimacy(mutual confiding),and reciprocal services that characterize the ties [40].This study measures interaction strength betweenertoehby interaction frequencyfrh.Normalized interaction strength betweenerandehis calculated by:

wherefrmaxandfrminare the maximum interaction frequency and minimum interaction frequency fromer～to other DMet,t∈{1,2,...,m},respectively.Interaction frequencySIrhis assumed to be fixed during the decision-making process.Note that interaction strengthSIrhmay not be the same asSIhr.The reason is thatSIrhrefers to interaction strength betweenerandehevaluated byer,whileSIhris interaction strength betweenehanderevaluated byeh.

Letλbe a weight for balancing the importance of connection strength and interaction strength.For example,λ＜0.5 reflects that the interaction strength is more informative than connection strength.In this paper,λtakes 0.4.The strength of social ties betweenerandeh(evaluated byer) is defined by aggregating the connection strength and interaction strength oferandeh:

2.2 Possibility Distribution Based Hesitant Fuzzy Element

LetX={x1,x2,...,xn}(n≥2) be a finite set of alternatives.E={e1,...,er,...,em} is a set of DMs.

Each DM gives a judgment on the various alternatives.As we know,preference relations are a classical and powerful preference structure to represent the preferences in GDM problems.Fuzzy preference relations(FPR)have been found to be effective when dealing with uncertain information[41–45].Therefore,this study uses FPR to represent each DM’s opinion on alternativesX.

Definition 2[7]: A FPR onXis represented by a matrixB=⊂X×X,wherebij=∈[0,1] indicates the assessment for the pairIn addition,the additive reciprocity holds,that is,bij+bji=1,i,j=1,2,...,n.

Definition 3[7]: The possibility distribution-based hesitant fuzzy element (PDHFE) can be expressed as follows:

wherehl,l=1,2,...,#hare the membership degrees and #his the cardinality ofh.pldenotes the possibility ofhl.If there is only one membership value in a given PDHFE,then the bracket can be dropped;for example,we have 0.5=0.5=0.5(1).For simplicity,h(p)=hp.

Definition 4[7]: A PDFPR onXis given by the matrixH=⊂X×X,wherehpij=is a PDHFE.Moreover,thehpijmeets the following conditions:

wherehlijis thelth possible value ofhijandplijis the probability ofhlij.

Definition 5[7]:The expected value or mean forhpcan be defined as follows:

Definition 6[7]:The distance betweenhp(1)andhp(2)is defined as follows:

wherehp(1)=andhp(2)=are two PDHFEs.It is easy to see that 0 ≤≤1.

3 Consensus Framework and Model for the LGDM

3.1 Problem Description and Consensus Framework

Suppose that there aremDMs who provide their preferences fornalternatives,and the preference relations of DMs can be expressed by FPR.WhereE={e1,e2,...,em} representsmDMs,X={x1,x2,...,xn}representsnalternatives.The pairwise comparison matrix given by the decision maker is denoted asBk=,k=1,2,...,m.This study also collects the number of likes and reviews that the DMs interact with other members in their daily lives,and counts the frequency of interaction between DMs.A trust network is constructed by calculating the degree of trust by the interaction frequency between DMs.For the three aspects mentioned in the introduction,the paper will take the following solutions,and Fig.1 illustrates the overall solution clearly:

(1)Firstly,according to the social relations between DMs,a directed social relationship network can be constructed.Then the trust relationships among the members are calculated.Using the Louvain method which has been widely used in large-scale network community detection[46],the large-scale social network is divided into several subgroups.This part is detailed in Section 3.2.

(2) Secondly,the weight of the DMs in the subgroup and the weight of each subgroup based on trust relationships are calculated by combining the SNA and the Louvain method,then the consensus index is obtained.Details of trust weight determination and consensus measure are given in Section 3.3.

(3) Thirdly,if the group consensus does not reach the predefined threshold,the feedback mechanism considering the trust relationship between the members is used to adjust the consensus until the threshold is reached,and the network will change during this process.Details of the consensus reaching process are given in Section 3.4.

(4) Finally,the DMs’preferences are aggregated according to the network relations,and the alternatives are sorted to select the best ones.

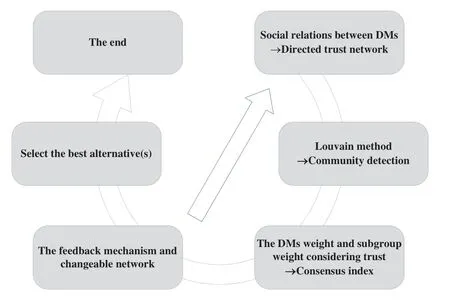
Figure 1 :The overall solution for LGDM problems based on trust relation and changeable network

3.2 Trust Weight Determination and Consensus Measure

In determining the weight of individual DM and the weight of each subgroup,compared with weighting based on network degree centrality or subgroup size,the trust weight and the network weight are fully considered.Firstly,this study uses the Louvain method to classify DMs,and obtains the comprehensive weight of each DM by the network weights and trust weights.Then,based on the reciprocal of the distance from each subgroup to the network center,the weight of each subgroup is calculated.Finally,based on the work of Herrera-Viedma et al.[47],the main steps of the consensus measure are listed.In addition,the weights for individual DM and the weight of each subgroup will change accordingly in the consensus reaching process.

3.2.1TrustNetworkandLouvainMethodinCommunityDetection

Community,also called a cluster or module,is a group of vertices which probably share common properties.Community detection refers to the recognition of modules and their boundaries based on the structural positions of vertices and the classification of vertices [48].The community detection method is the key based on a trust network for DMs to reduce dimensionality clustering.Some methods have been developed,such as the GN method[49],the spin-glass method[50],the random walk community detection[51],the label propagation method[52]and so on.The Louvain method is a commonly used community detection method,which is based on the modularity theory proposed by Blondel et al.[46].This method is an agglomerative clustering algorithm,which reveals the complete hierarchical community structure of the network and can cluster subgroups automatically without setting the initial number of subgroups.Therefore,this study uses the Louvain method for DMs in LGDM problems.

Assuming that a network hastnodes,the algorithm of the Louvain method can be expressed as follows[39]:

Step 1:Each node in the network is treated as a separate community.In the beginning,the number of communities is the same as the number of nodes.

Step 2:Assign each node to the community according to the node near each node,calculate the value of ΔQbefore and after the module allocation,and record the maximum ΔQvalue of the node.IfmaxΔQ＞0,then the node ˆdαis assigned to the community where the node with the maximum ΔQvalue is located,otherwise,it will remain unchanged.

The definition of ΔQis as follows:

Step 3:RepeatStep 2until the network in the community no longer changes.

Step 4: Streamline the entire network and treat the nodes in a community as a new node.The weights between nodes within the community are converted to the weights of the new nodes.The weights between the edges of the community are converted to weights between the edges of the new nodes.The boundary value of the weight is 1.

Step 5:RepeatSteps 1–4until the modules of the entire network no longer change.

3.2.2TheComprehensiveWeightofEachDecisionMaker

(1)Network weights of each DM

SetVnodes in the network.Firstly,the degree centralityCD(er) and the eigenvector centralityCE(er) of each nodeer(r=1,2,...,m) are calculated by using Pajek software,and then they are standardized[5]:

Combining the normalized degree centralityC′D(er)with the eigenvector centralityC′E(er),calculate the mixed center degreeCF(er)of the nodeer(r=1,2,...,m):

According to[49],the value ofσis generally 0.5.

Suppose thatmnodes in the network are divided intopsubgroups,and there aresnodes in the subgroupGk(1 ≤k≤p),the network weight of the nodeer(er∈ck,1 ≤r≤s)can be calculated as:

(2)Trust weights of each DM

Assigning weight to each DM is an important part of the decision-making process and plays a key role in obtaining the final solution.For online social networks,historical interaction information can provide a reliable source for accessing DMs.

Social influence is defined as the individual’s thoughts,feelings,attitudes or behaviors can affect others when interacting with other individuals or groups.DMs with higher social impact have the ability to influence the opinions of other members [47].Using social network analysis techniques,the social impact of each DM in the group can be obtained.The more social relations a person has with others,the more influence the decision maker will be.In the social network analysis method,the centrality of the in-degree is used to quantify the social influence of DM in a network,and the social influence can reflect the importance of DM to a certain extent.Therefore,the social impact ofer,r=1,2,...,mis defined by Eq.(15),and the trust weight is determined by Eq.(16).

Then the comprehensive weight of each DM can be calculated asw=θwr2+(1-θ)wr1.

3.2.3TheWeightofEachSubgroup

The network weight between subgroups can be calculated from the reciprocal of the distance from each subgroup to the network center.The further the distance,the smaller the weight.The main steps for calculating weights are shown below[5]:

Step 1:Calculate the fusion centrality of the network.

whereM={e1,e2,...,er,...,et}represents all nodes of the network.

Step 2:Calculate the fusion centrality of each subgroup.

whereM=Sk={e1,e2,...,er,...,es},|Sk|represents the number of all nodes of the subgroupck,eris the nodes in the subgroupck.

Step 3:Calculate the relative distanceλ′kofCF(ck)andCFin communityck.

Step 4:Standardize the weightλ′k.

The trust relation between subgroups can be reconstructed by treating all nodes in a subgroup as a new node,and then calculating the trust weights between subgroups.Finally,the network weights and trust weights of the subgroups are integrated,and the comprehensive weights of the subgroups are obtained.

Next,the consensus measure will be computed based onHt,t=1,2,...,K.Based on the work of Herrera-Viedma et al.[47],the main steps of the consensus measure are as follows:

Step 1:Calculate the similarity matrix.Letandcorrespond to the probability distribution of subgroupGkandGtbased on the fuzzy preference relationship.Wherehpij,k=orhpij,t=is a probability distribution based on hesitant fuzzy elements.For each pair of subgroupsGkandGt(k＜t,t∈{1,2,...,K}),the similarity matrixSMkt=is calculated as follows:

whereis the similarity of the subgroupsGkandGtwith respect to the alternatives1,2,...,n.According to definition 6,can be expressed as follows:

Step 2:Calculate the consensus matrix.By aggregating the similarity matrix of each pair of subgroups(Gk,Gt),a consensus matrixCM=can be obtained.Then this study normalizes the weights of the subgroup pairs(Gk,Gt),ωktis defined as follows:

cmijcan be expressed as follows:

Step 3:Calculate the large-scale group consensus index(LGCI).

(1) Calculate the consensus degree of the pair of alternatives.The consensus degreecpijof the alternatives paircan be obtained from the consensus matrixCM=cpijcan be expressed as follows:

(2)Calculate the consensus degree of the alternatives.The consensus degreecai,i=1,2,...,nof each alternativexican be calculated as follows:

(3)Calculate the consensus degree of the preference relationship.This study refers to the consensus degree of the large group preference relationship as the consensus index LGCI,and the formula is as follows:

3.3 Consensus Reaching Process Based on Social Network Updating

Based on the above discussion,this study can get consensus at different levels.Assumeis a predefined threshold.IfLGCI≥,all DMs reach a higher level of consensus and the consensus adjustment process ends.Otherwise,this study will adjust the preference values of DMs with low consensus.In this section,this study proposes a feedback mechanism to help DMs in each subgroup change their preferences based on[37].The mechanism consists of four identification rules and two direction rules to detect which subgroups need to change their preferences,and the DMs’preference relations will change during identification,clustering,and location.

Moreover,the strength of ties between members shows the trust degree between those members.DMs with strong trust relationships have a greater impact.In the process of interaction,DMs with strong trust relationships will affect the preferences of DMs with weaker trust relationships.At the same time,the trust relation between DMs will also change.Therefore,this study will reflect the results of the feedback in the social network and change the connection between DMs to achieve a higher consensus faster according to the trust relationship between DMs.

3.3.1IdentificationRules

The identification rules can obtain alternative comparison pairs,subgroups,and DMs continuously and accurately.Therefore,DMs can change their preferences in a precise way.

Identification Rule 1:Identify alternatives whose preferences need to be changed.The identified alternatives can be expressed as follows:

Identification Rule 2: Identify the locations that need to be changed.For anyxi∈ALT,the identified set of locations can be expressed as follows:

Identification Rule 3:Determine the ideal and non-ideal sets for each identified part.For(i,j) ∈Posi,ideal setand non-ideal setcan be expressed as follows:

Identification Rule 4: Identify the DMs who need to change their preferences.For the identified non-ideal setthis study can use a deeper consensus measure to determine the DMs with only the lowest level of consensus.

The DMs in the non-ideal setcan be expressed asG(k-)=is the number of DMs inNote that the FPR ofekyisBky=Similarly,the DMs incan be represented asis the number of DMs inThe preference ofGk+xi,xjis a PDHFE,which can be expressed byThe average preference forhpij,k+can be calculated as follows:

Set thresholdsβ.The DMs who need to change their preferencescan calculate as follows:

3.3.2DirectionsRulesandNetworkAdjustment

For eacheky∈EXPSij,there are two directions rules as follows[10]:

Directions Rule 1:Ifbij,ky＜thenekyneeds to increase the preference value of

Directions Rule 2:Ifbij,ky＞thenekyneeds to decrease the preference value of

One way to achieve the direction rule is to provide a set of values foreky∈EXPSij.Since each element in the initialekybelongs toS[0.1,0.9],it is better to set the range of values of all recommended values in this interval.

LetRndij,k+=whereRoundis a method to find the nearest discrete membership in the range ofS[0.1,0.9].Then the recommended setekycan be expressed as follows:

By the opposite nature of each other,the preferenceekyandcan be automatically adjusted and updated.

After completing the above adjustment process,the final step is to modify the original social network.

Step 1: Let (i,j) be the position that needs to be modified,is a set of DMs whose opinions need to be modified.

Step 2:Calculate theTSrhvalue according to Eq.(5),and use it as an index to evaluate the trust degree between members.Find the most trusted memberin the ideal set,denoted as

Step 3:Modify the original social network.According toandF′=connecte′iandfi′,wherei=1,2,...,v.

3.4 The Procedure of the Proposed Method

The main steps of the LGDM consensus problem are summarized below.Fig.2 shows the framework of the proposed method.

Part 1:Determine the network structure of the LGDM problem.

(1)The set of DMs and alternatives are represented byandX={x1,x2,...xn},respectively.

(2)For each DM,a fuzzy preference matrixBk=,k=1,2,...,mis established.DMs tend to use fuzzy preference relationships to express their opinion.Next,the consensus threshold,parameterβand the maximum number of iterationsMaxroundare set.

(3) The Louvain method is used to determine subgroups of large-scale networks.Suppose this study getsKrsubgroups,denoted by

Part 2:Calculate the trust weight and consensus measure.

(1)Calculate the weights of thetth(1 ≤i≤m)DM and thetth(1 ≤t≤Kr)subgroups.

(2)Calculate the PDFRP for each subgroup.

(3)Calculate the consensus of each subgroup.

Subgroup consensus can be obtained according to Section 3.3.Set the consensus isLGCIrin the current round.IfLGCIr≥orr＞Maxround,go to Part 4;otherwise,proceed to Part 3.

Part 3:Consensus reaching process.

(1)Determine the identified DM as the corresponding new collection.

According to the four identification rules proposed in Section 3.3.1,the set of non-ideal DM can be expressed asEXPSi-j,r.

(2)Direct the DMs inEXPSi-j,rto modify their preferences.

Modify the FPR of the DM inEXPSi-j,rbased on the two direction rules in Section 3.3.2.Next,letr=r+1,the modified FPR is still represented byBk,r,k=1,2,...,m.

(3)Modify the social network.

Part 4:Select the best alternative(s).

(1)Based on the final adjusted network,the weight of each DM within the subgroup and subgroup weights are recalculated,and then the final pairwise comparison matrix is obtained by aggregating the preference matrix of all subgroups for each pair of alternatives according to Eqs.(21)–(24).

(2)After obtaining the final pairwise comparison matrix,the final ranking result is obtained by subtracting the sum of each column value from the sum of each row value of each alternative[53].

(3)Rank all alternatives in descending order by the gap between the column value and row value and choose the alternative with the smallest gap as the best alternative.

4 Case Study

4.1 Case Description

Twenty travel enthusiasts with certain social connections are denoted asE={e1,e2,...,e20}.They are going to choose the best destination for vacation travel.After pre-evaluation,the following four alternatives are selected,denoted asX={x1,x2,x3,x4},wherex1=Gulangyu Islet;x2=Suzhou Gardens;x3=Lijiang Ancient City;x4=Dujiang Dam.Each member evaluates and judges the four alternative tourist destinations by the way of pairwise comparison.This study obtains the pairwise judgment matrixBk,k=1,2,...,20 as shown below[7]:

The social network relations between the 20 travel enthusiasts as shown in Fig.3.

In Fig.3,each travel enthusiast is represented in the network as a node with different colors and used to distinguish the number of ingress connections of the DMs.For example,the DMe18has the largest indegree in the group,so the color of node 18 is dark blue.In contrast,node 13 is colored yellowish because it has only one ingress connection frome2.

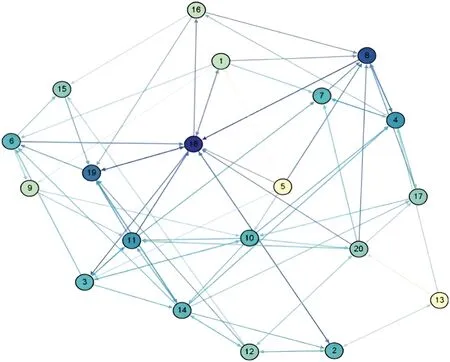
Figure 3 :DMs’social network

4.2 Method Application

4.2.1ClassificationofNetworkUsingLauvainMethod

A network corresponding to Fig.3 is constructed in the complex network analysis tool Pajek,as shown in Fig.4,where nodesv1-v20correspond to nodes1–20in Fig.3,respectively.

Using the Lauvain package included in the Pajek software,automatic classification is performed to form the classification results as shown in Fig.5.The subgroup is represented by the setwhich is divided into three subgroups.The subgroup consisting of yellow nodes isG1,the subgroup consisting of green nodes isG2,and the subgroup consisting of red nodes isG3,i.e.,G1={v1,v3,v5,v6,v9,v10,v11,v18},G2={v2,v12,v14,v15,v16,v19},G1={v4,v7,v8,v13,v17,v20}.

4.2.2CalculatetheTrustWeightandConsensusMeasure

For the subgroupG1,the network is shown in Fig.6.

According to the original data required by the software and the original data required for the centrality of the feature vector,the network weight of each node in the subgroupG1can be obtained according to the Eq.(14),as shown in Table 1.

Table 1 : Weights of nodes in subgroup G1

According to the network weights and trust weights,the weight of each DM is aggregated.And this study takesθ=0.2,then,the comprehensive weights of the nodes in the subgroupG1are shown in Table 1.

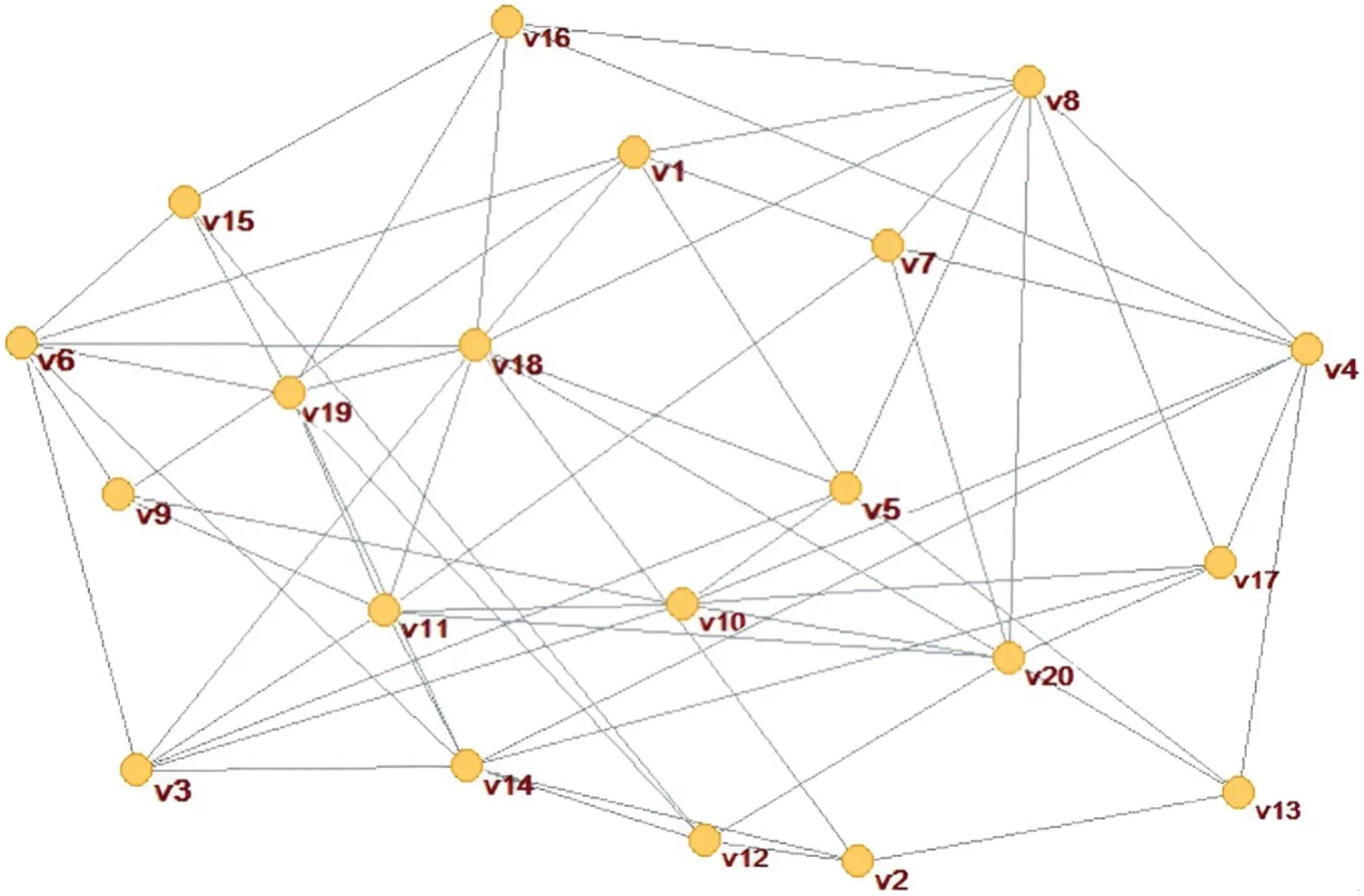
Figure 4 :Network constructed in Pajek software

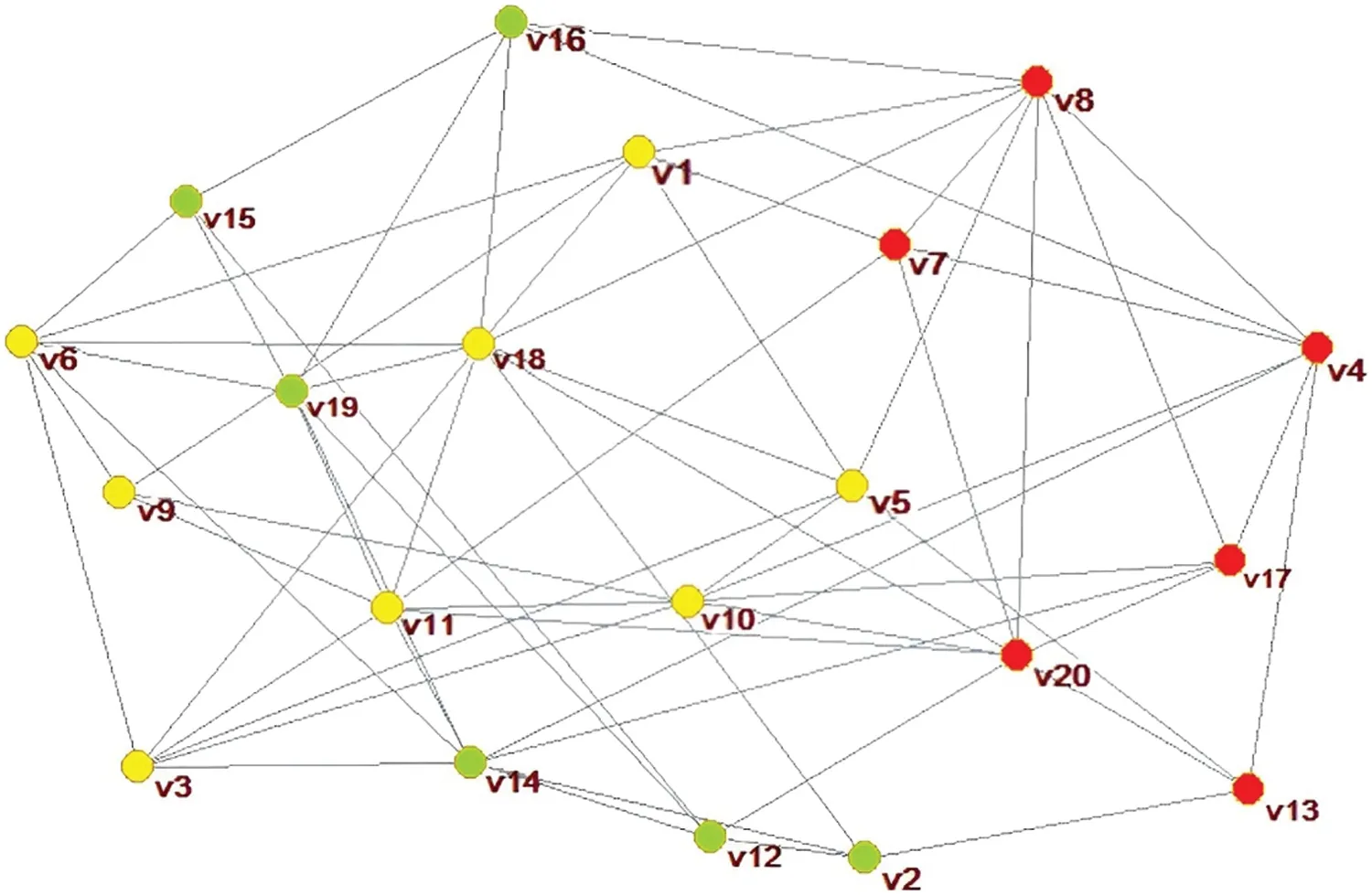
Figure 5 :Social network clustering analysis results

According to the calculation results by Pajek software and Section 3.2,the network weight of each subgroup is{0.05,0.04,0.19}.

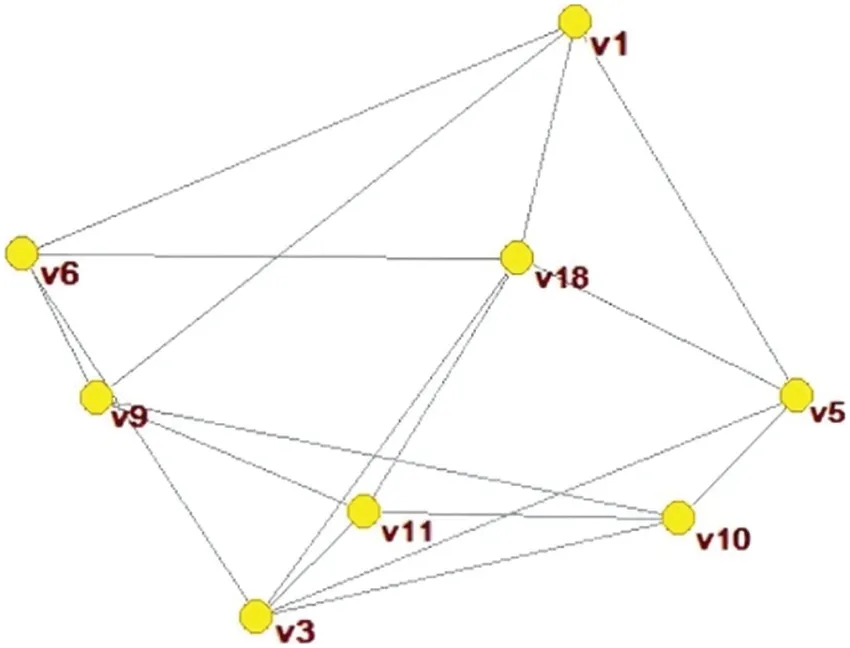
Figure 6 :Network of subgroup G1

Considering each subgroup as a node,Fig.3 can be abstracted into the structure shown in Fig.7,where the direction of the edge represents the relationship between nodes,and the thickness of the edge represents the connection strength.

The trust weights between subgroups are{0.40,0.26,0.34}.

Similarly,by aggregating the network weights and trust weights of each subgroup,the comprehensive weight of each subgroup can be obtained{0.33,0.22,0.45}.

According to their preference for alternatives provided by the 20 DMs through FPR,the preference relationship of each subgroup also forms a probability distribution based on fuzzy preference relations[51].According to Section 3.4,the correspondingGk,k=1,2,3 has three PDFPRs,which can be expressed as

For the subgroupG1,the PDFPR can be expressed as follows:

hp12,1={0.1(0.14),0.3(0.10),0.4(0.25),0.6(0.25),0.7(0.13),0.9(0.13)}

hp13,1={0.4(0.38),0.6(0.49),0.9(0.13)},

hp14,1={0.2(0.13),0.4(0.10),0.6(0.29),0.7(0.22),0.8(0.26)},

hp23,1={0.1(0.10),0.3(0.28),0.6(0.27),0.7(0.13),0.8(0.10),0.9(0,12)}

hp24,1={0.4(0.29),0.5(0.10),0.7(0.26),0.8(0.23),0.9(0.12)},

hp34,1={0.3(0.14),0.4(0.23),0.6(0.13),0.7(0.15),0.9(0.35)}.

For the subgroupG2,the PDFPR can be expressed as follows:

hp12,2={0.3(0.29),0.4(0.15),0.6(0.21),0.7(0.15),0.9(0.20)},

hp13,2={0.2(0.21),0.4(0.30),0.6(0.18),0.7(0.31)},

hp14,2={0.2(0.15),0.3(0.21),0.4(0.18),0.5(0.15),0.8(0.31)},

hp23,2={0.1(0.30),0.3(0.11),0.4(0.21),0.6(0.18),0.8(0.20)},

hp24,2={0.2(0.30),0.3(0.21),0.6(0.29),0.7(0.20)},

hp34,2={0.1(0.20),0.3(0.11),0.4(0.51),0.6(0.18)}.

For the subgroupG3,the PDFPR can be expressed as follows:

hp12,3={0.1(0.17),0.2(0.17),0.4(0.38),0.6(0.27)},

hp13,3={0.2(0.08),0.4(0.35),0.6(0.17),0.7(0.22),0.8(0.17)},

hp14,3={0.1(0.35),0.3(0.08),0.4(0.17),0.6(0.39)},

hp23,3={0.3(0.19),0.4(0.30),0.5(0.16),0.6(0.17),0.8(0.17)},

hp24,3={0.3(0.08),0.4(0.35),0.6(0.17),0.8(0.39)},

hp34,3={0.4(0.08),0.6(0.17),0.7(0.57),0.8(0.17)}.

According to Section 3.4,the consensus degree of the three subgroups can be calculated.First,the similarity matrixes between subgroups are calculated,and the results are as follows:

According to Eq.(13),the normalized weights between subgroups are{0.22,0.47,0.31}.

Second,the consensus of the group is calculated,and the consensus matrix is as follows:

The consensus degree between alternative pairs iscpij=cmij,i,j=1,2,3,4.

Third,the consensus degree at the level of the alternative isca1=7523,ca2=7461,ca3=7594,ca4=7376.

Finally,the consensus degree of the group isLGCI=0.7488.

4.2.3ConsensusReachingProcess

Set=0.8.BecauseLGCI,the feedback adjustment mechanism can be activated.According to Rule 1 and Rule 2 in Section 3.3.1,the preference relationship on (x2,x3) needs to be modified.According to Rule 3,ideal subgroups and non-ideal subgroups can be obtained:

CLU2+3={G3},CLU2-3={G1,G2}.

Let the parameterβ=0.3 and calculateExpect=0.495,then this study can identify the DMs that need to readjust the preference value in subgroupG1and subgroupG2.

DMs in subgroupG1:e5,e9,

DMs in subgroupG2:e15,e16.

Find the most trusted person for DMse5,e9,e15,e16in subgroupG3.The most trusted persons fore5,e9,e15,e16aree8,e17,e8,e8,respectively.The new preference value of the DM is changed to the preference value of the most trusted person[52].

First round of adjustment:

According to Section 3.2.1,this study can get a new social network based on the Louvain method and a new subgroup classified as shown in Figs.8 and 9.

As can be seen from the Fig.9,three new subgroups can be obtained in this adjustment:G1={v1,v3,v5,v8,v18},G2={v2,v6,v12,v14,v15,v16,v19},G3={v4,v7,v9,v10,v11,v13,v17,v20}.Then the trust weight and the network weight are integrated to determine the relative weight between the subgroups as shown in Table 2.And the weight of each subgroup is{0.21,0.25,0.54}.

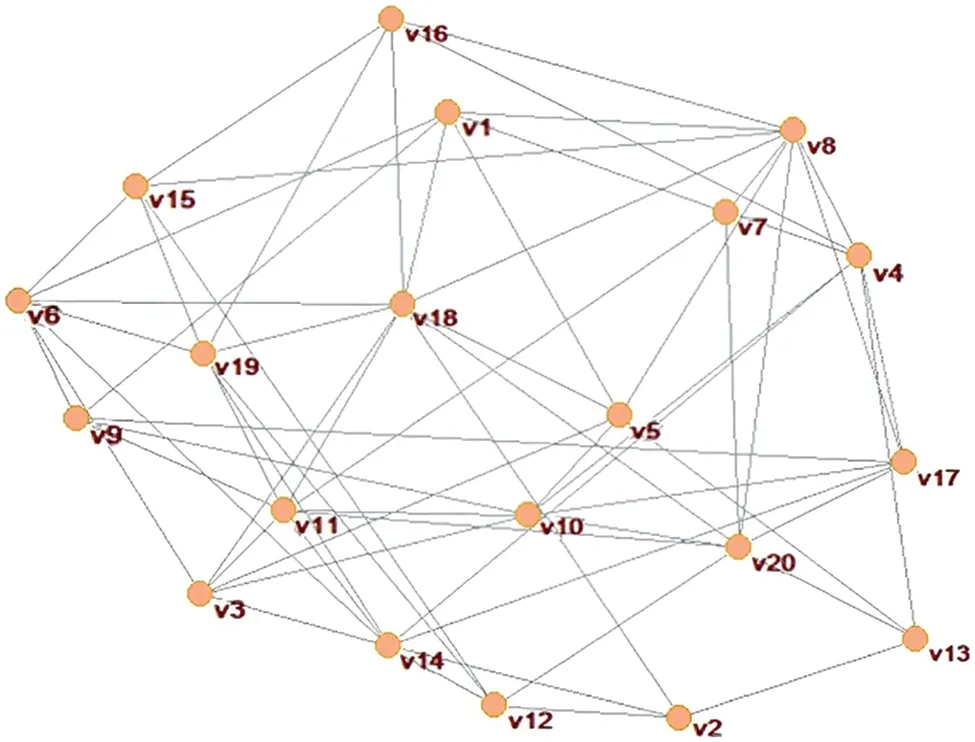
Figure 8 :Network in the first round of adjustment

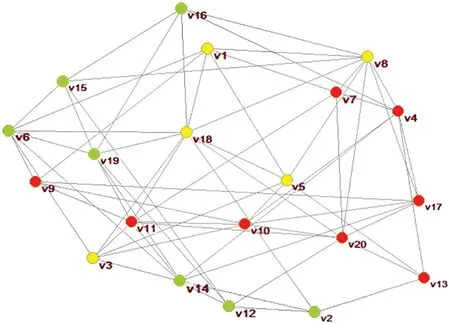
Figure 9 :Classification result

For the subgroupG1,the PDFPR can be expressed as follows:

hp12,1={0.1(0.16),0.4(0.42),0.6(0.25),0.9(0.17)},

hp13,1={0.4(0.43),0.6(0.16),0.7(0.24),0.9(0.17)},

hp14,1={0.2(0.25),0.4(0.18),0.6(0.40),0.8(0.17)},

hp23,1={0.3(0.25),0.4(0.42),0.6(0.16),0.7(0.17)},

hp24,1={0.4(0.16),0.5(0.18),0.7(0.25),0.8(0.41)},

hp34,1={0.3(0.16),0.4(0.35),0.6(0.25),0.7(0.24)}.

For the subgroupG2,the PDFPR can be expressed as follows:

hp12,2={0.3(0.38),0.4(0.12),0.6(0.19),0.7(0.13),0.9(0.17)},

hp13,2={0.2(0.19),0.4(0.25),0.6(0.29),0.7(0.26)},

hp14,2={0.2(0.12),0.3(0.19),0.4(0.15),0.5(0.13),0.7(0.14),0.8(0.26)},

hp23,2={0.3(0.09),0.4(0.44),0.6(0.15),0.8(0.31)},

hp24,2={0.2(0.25),0.3(0.19),0.6(0.24),0.7(0.17),0.8(0.14)},

hp34,2={0.1(0.17),0.3(0.09),0.4(0.44),0.6(0.15),0.9(0.14)}.

For the subgroupG3,the PDFPR can be expressed as follows:

hp12,3={0.1(0.12),0.2(0.13),0.4(0.29),0.6(0.33),0.7(0.14)},

hp13,3={0.2(0.07),0.4(0.45),0.6(0.37),0.8(0.12)},

hp14,3={0.1(0.30),0.3(0.07),0.4(0.12),0.6(0.28),0.7(0.10),0.8(0.14)},

hp23,3={0.3(0.31),0.4(0.07),0.5(0.24),0.6(0.26),0.8(0.13)},

hp24,3={0.3(0.07),0.4(0.45),0.6(0.12),0.7(0.14),0.8(0.13),0.9(0.10)},

hp34,3={0.4(0.07),0.6(0.13),0.7(0.45),0.8(0.12),0.9(0.24)}.

The new similarity matrixes between subgroups are:

The normalized weights between pairs of subgroups are{0.17,0.38,0.45}.

Then the consensus of the group is calculated,and the consensus matrix is as follows:

ca1=0.7574,ca2=0.7695,ca3=0.7742,ca4=0.7325.

The consensus degree of the large groupLGCI=0.7584.

The preference pairs that need to be modified are(x1,x2),(x1,x4).According to the above method,after three more modifications,the consensus degree of the large group isLGCI=0.7976.Since 0.7976 is very close to the set threshold of 0.8,the adjustment is considered to be over.

4.2.4SelecttheBestAlternative(s)

The network obtained at the end of the final adjustment is shown in Fig.10.

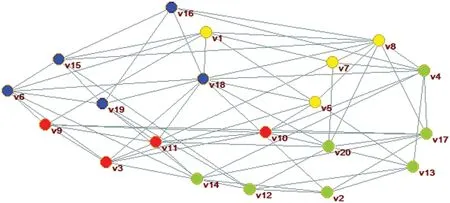
Figure 10 :Classification network in the last round of adjustment

According to the network structure,the network weights and trust weights of the nodes are obtained,and the relative weights of the nodes in each subgroup are shown in Table 3.And the relative weights between the subgroups are{0.22,0.33,0.20,0.25}.

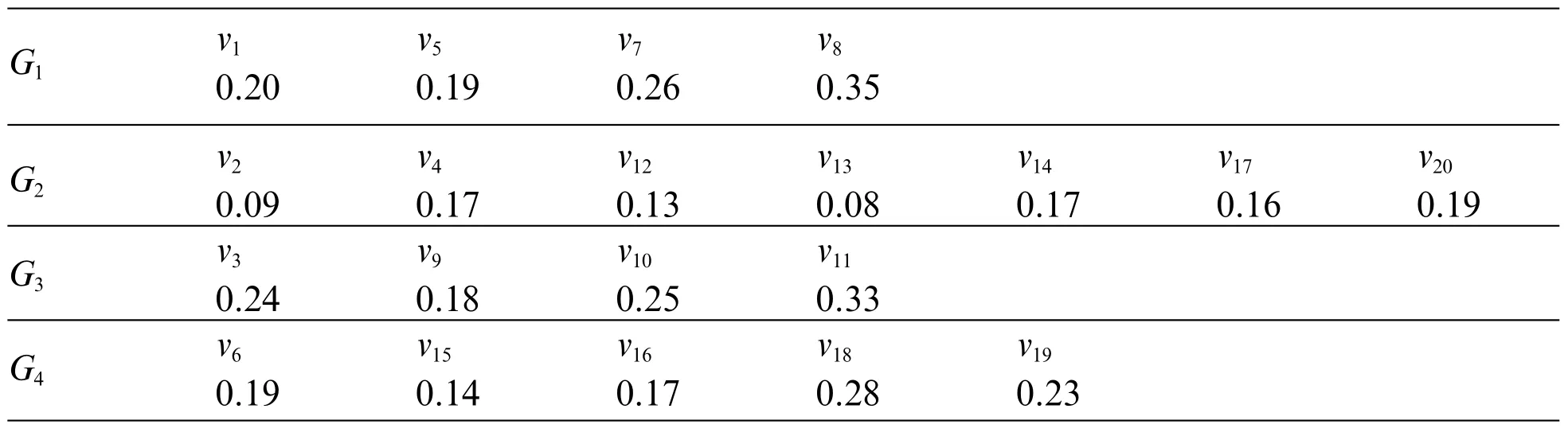
Table 3 : Relative weight of each node in subgroup

According to Eqs.(21)–(24),the preference of each DM is gathered within the subgroup,as shown below:

After obtaining the final pairwise comparison matrix,the final ranking result is obtained by subtracting the sum of each column value from the sum of each row value of each alternative [53].According to the calculation,this study obtains|x1|=0.04,|x2|=0.2,|x3|=0.1,|x4|=0.26|,thusx1≻x3≻x2≻x4,x1=Gulangyu Islet is the best alternative.

5 Comparative and Experiment Analysis

5.1 Comparative Analysis

The proposed model considers the trust relationship between DMs,and daily social data are combined when calculating trust weights.The novel Louvain method is adopted in the classification of large groups,which has certain advantages compared with the traditional clustering method.In addition,this study also fully integrates real life when designing the feedback mechanism,and reconstructs the network through trust relations.This section compares the proposed method with other methods,as shown in Table 4.

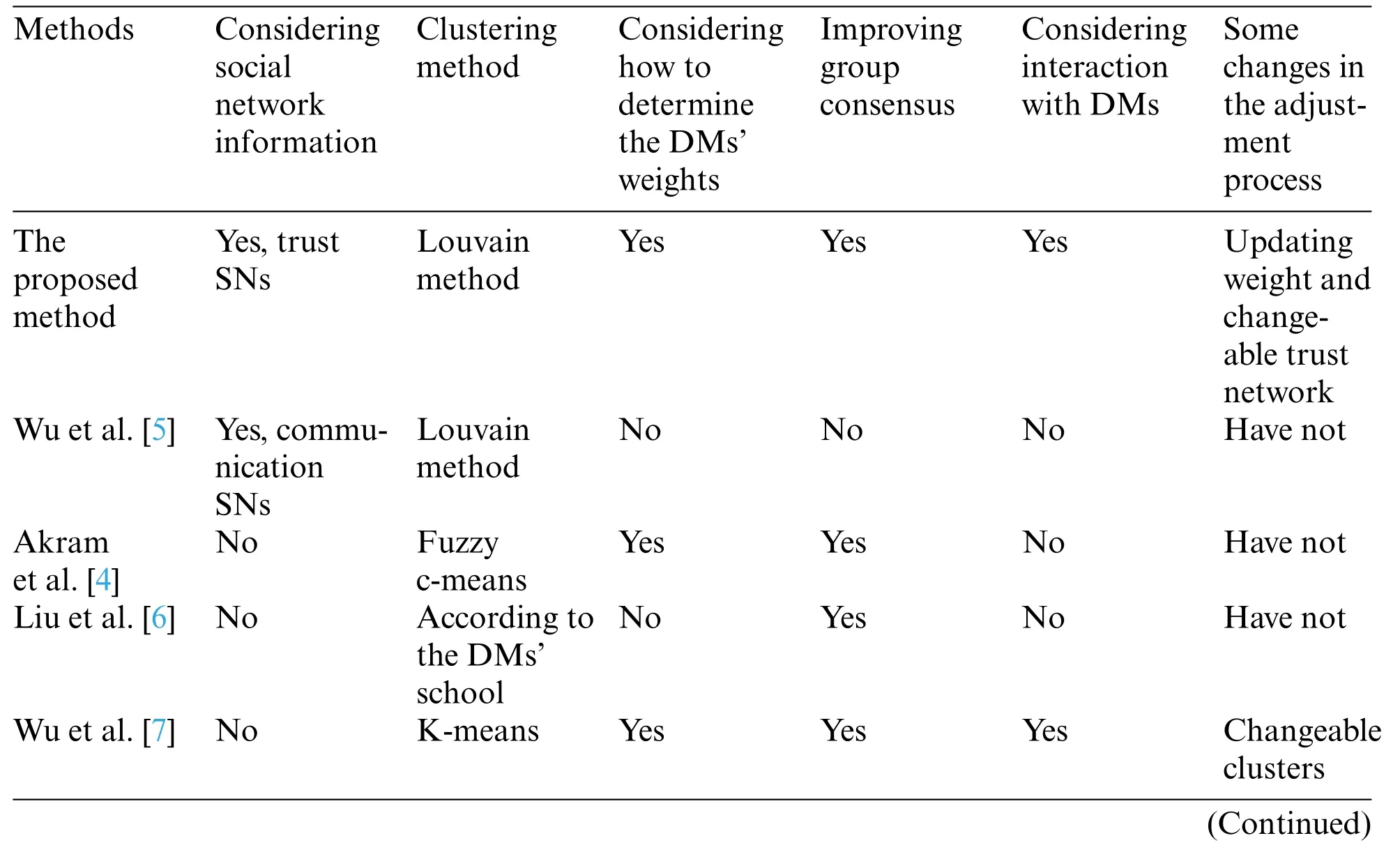
Table 4 : Comparison of different methods for LGDM

(1)Comparison with the LGDM with the clustering methods.

Akram et al.[4] used fuzzy c-means to cluster the fuzzy preferences,computed the consensus degree and improved consensus.But Akram et al.[4]did not consider the social network information.Liu et al.[6]classified the DMs according to the practical situation(DMs’school).According to the percentage distribution and the decision weights,the dominance degrees on pairwise comparisons of alternatives are calculated,and a ranking of alternatives can be determined.However,Liu et al.[6]did not involve consensus improvement and interaction with DMs.A two-stage method to support the consensus-reaching process for large-scale multi-attribute group decision making was presented by Xu et al.[54].The first stage classified the group into sub-subgroups by using the SOM in order to obtain preference of each sub-cluster.Wu et al.[55] developed a solution for LGDM,which used linguistic principal component analysis to reduce the dimensions of the attributes and used fuzzy equivalence clustering with linguistic information aggregate the preferences of the DMs,respectively.Wu et al.[56]incorporated clustering analysis and information aggregation operator into LGDM with interval type-2 fuzzy sets and used fuzzy equivalence clustering analysis to classify DMs to reduce the dimension of the DMs.However,[6]and[55]did not consider the consensus and interaction with DMs.At the same time,they all did not consider the relationship among DMs,such as communication,trust or cooperation.

Wu et al.[5] have built a large-scale undirected and unweighted network of 50 people.The relationship among DMs in the network is communication relationship and the Louvain method is also applied.The objective relationship of trust in the real world is very important in decision-making,but Wu et al.[5] did not take it into consideration.Moreover,it is not involved in the consensus measure and CRP.This study takes the trust relationship through the entire decision-making process,from social network construction and clustering,to weight determination and consensus measure,and finally to CRP and changeable networks.

(2)Comparison with the LGDM with the changeable cluster.

Some existed studies have considered the changeable cluster for LGDM.For example,the k-means clustering method based on Euclidean distance under possibility information was extended to classify the whole group into manageable subgroups [7].The results showed that the twenty DMs were clustered into three clusters {G1,G2,G3},whereG1={e1,e3,e5,e6,e9,e10,e11,e18}G2={e2,e12,e14,e16,e19},G3={e4,e7,e8,e13,e17,e20}in the first round.Moreover,the number of clustersKneeds to be set artificially.Consensus measures based on the distance measure were computed and the clusters in each interactive round were allowed to change.Although the subgroup changes during each round of adjustment,the number of subgroups does not change.And the consensus level increased from 0.6925 to 0.7861 and then to 0.7970.

Due to the low initial consensus of [7],the consensus is improved quickly after three rounds of adjustment; The initial consensus of this study is higher,after three rounds of adjustment,the predefined consensus level is also reached.Compared with the results of [7],The final consensus of this study is higher,which illustrates the effectiveness of the proposed method.In addition,since the decision preference information used by the two methods is the same,the different results of the two methods indicate that the SN information can amplify the difference between the alternatives,which means that social information about the DM does affect the outcome of the LGDM problem.When DM has similar preferences,it is reasonable to consider social information,which will be beneficial to SNA.

The proposed model in this study not only combines social network information,but also the number of subgroups is determined automatically.At the same time,in each round of adjustment process,not only the number of subgroups changes,but also the internal network structure of subgroups changes,which can more realistically aggregate the preference matrix of DMs,the optimal solution can be obtained in a simpler and more efficient way.

5.2 The Experiment Analysis

In order to determine the appropriate coefficientθ,a simulation analysis is required.When the value ofθare different,the consensus reached later will be different[57],as shown in Fig.11.Whenθis 0.2,the consensus index is obtained.Therefore,this study takesθ=0.2 In the future case application,the coefficient can be selected according to the actual situation.

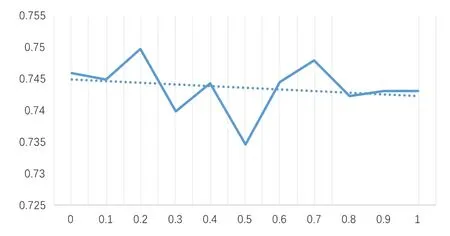
Figure 11 :Simulation analysis of θ

6 Conclusions

In previous studies,DMs were independent of each other in the GDM problems.However,in most practical decision situations,DMs are socially related to each other rather than independent of each other.Moreover,consensus improvement is becoming increasingly important for DMs and stakeholders.This study provides a new perspective on LGDM problems and the main contributions are as follows:

First,this study considers the social trust relationship between DMs for the LGDM problems,builds the social network between DMs,and uses the Louvain method to detect community based on the trust relationship.Social networks built on trust relationships are more convincing than building networks based solely on DMs.

Second,this study fully considers the trust weight and the network weight in the process of determining the weight of individual DMs and the weight of each subgroup.Compared with weighting based on network degree centrality or subgroup size,it is more convincing to assign weights based on trust relationships and to make corresponding changes in weights in the feedback adjustment process.In the process of obtaining the final weight,the parameterθis simulated and analyzed.Finally,a value ofθwhich is most suitable for the example is selected.

Third,the trust network in the proposed model allows for changes.Individual DMs are able to modify their preferences in the CRP,so the trust relationship will change,which will make the number of subgroups and members of each subgroup likely to change.And the interaction of trust relations is fully considered in the adjustment process.This is more in line with the reality that the influential DMs in the network will influence the opinions of the surrounding DM and enhance their trust.

Some significant opportunities for future work should be pointed out.

Firstly,this study determines the social network,trust weights and network weights by organizing social connections between DMs and the interaction frequency on social platforms.How to more scientifically measure the relationship between DMs is worth studying and improving.Secondly,although the Louvain method has realized automatic classification of the network,the constructed network diagram is still an undirected graph.In fact,a directed network is more reasonable and applicable to represent the social connection between people,and the classification results may differ from undirected networks.If the automatic classification method of directed networks can be added to future research,it will be a good innovation.Finally,the two parameters are fixed in this study:the predefined threshold ofLGCIand parameterβ.The specific values of these parameters depend on the actual situation.In most studies,these two parameters are also set to a fixed value.If a reasonable algorithm can be designed to adjust these parameters in the consensus reaching process,the model will be more flexible.Considering non-cooperative behavior[58]and individual satisfaction[59]to extend our methods is also an interesting work in the future.

Funding Statement:The work was supported by Humanities and Social Sciences Fund of the Ministry of Education(No.22YJA630119),the National Natural Science Foundation of China(No.71971051),and Natural Science Foundation of Hebei Province(No.G2021501004).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.