Modeling Method of C/C-ZrC Composites and Prediction of Equivalent Thermal Conductivity Tensor Based on Asymptotic Homogenization

Junpeng Lyu,Hai Mei,2,Liping Zu,Lisheng Liu,2,★and Liangliang Chu,2

1Department of Mechanics and Engineering Structure,Wuhan University of Technology,Wuhan,430070,China

2Hubei Key Laboratory of Theory and Application of Advanced Materials Mechanics,Wuhan University of Technology,Wuhan,430070,China

ABSTRACT

This article proposes a modeling method for C/C-ZrC composite materials.According to the superposition of Gaussian random field,the original gray model is obtained,and the threshold segmentation method is used to generate the C-ZrC inclusion model.Finally,the fiber structure is added to construct the microstructure of the three-phase plain weave composite.The reconstructed inclusions can meet the randomness of the shape and have a uniform distribution.Using an algorithm based on asymptotic homogenization and finite element method,the equivalent thermal conductivity prediction of the microstructure finite element model was carried out,and the influence of component volume fraction on material thermal properties was explored.The sensitivity of model parameters was studied,including the size,mesh sensitivity,Gaussian complexity,and correlation length of the RVE model,and the optimal calculation model was selected.The results indicate that the volume fraction of the inclusion phase has a significant impact on the equivalent thermal conductivity of the material.As the volume fraction of carbon fiber and ZrC increases,the equivalent thermal conductivity tensor gradually decreases.This model can be used to explore the impact of material microstructure on the results,and numerical simulations have studied the relationship between structure and performance,providing the possibility of designing microstructure based on performance.

KEYWORDS

3D reconstruction;random heterogeneous media;microstructure;asymptotic homogenization;effective properties

1 Introduction

Carbon/Carbon composites have an irreplaceable position in the aerospace field.With the continuous development of modern science and technology,new aircraft put forward new requirements for the mechanical and thermal properties of thermal structural materials.When the hypersonic vehicle flies at the speed of Mach 05 or above,the highest temperature of the leading edge of the wing will reach 2700°C.In the aerobic environment of the atmosphere,most light materials cannot bear such a high temperature.Among the main thermal protection materials,metal is difficult to become an ideal anti-ablation material on aircraft because of its high specific gravity,high melting point and limited resources.C/C composite is one of the few materials that can maintain its mechanical properties at a high temperature above 2000 degrees Celsius,so it is necessary to study its thermal properties.In order to overcome the problem that C/C composites are easily oxidized in aerobic environment[1,2],ultra-high temperature ceramics (UHTC) have become the key to solve the problems faced by C/C composites because of its low density,low thermal expansion and low specific gravity [3–5].Since the appearance of C/C-UHTC composites,many scholars have studied its thermal properties by experimental means.Liu et al.[6] put forward a new weaving process,which can control the fiber tension to generate gradient orthogonal preforms.The thermal conductivity of C/C composites obtained by this method was studied,and the fiber volume fraction was analyzed.The ablation resistance of inclusion composites is higher than that of homogeneous composites,and the thermal conductivity increases with the increase of fiber volume fraction.Jayaseelan et al.[7]found that the addition of UHTC significantly improved the oxidation resistance and thermal properties of C/C composites.Li et al.[8] studied SiC/SiC composites with different heat transfer network structures.By assembling the fibers horizontally and in the thickness direction,the mechanical properties and thermal conductivity of the materials were improved to varying degrees.However,the thermal conduction channels in the thickness direction brought a lot of defects,which made the mechanical properties first increase and then decrease.It is not difficult to see that different structures and compositions will have a significant impact on the properties of composites.

Because of its low density and high melting point,ZrC has become one of the best candidate materials in ultra-high temperature ceramics.Zhang et al.[9] found that the introduction of ZrC into carbon/carbon composites can effectively reduce the ablation rate of C/C composites while maintaining the excellent properties of C/C composites,and studied the formation mechanism of C/CZrC-Cu prepared by infiltration method with Cu.The anti-ablation principle of C/C-ZrC composites was studied[10].ZrC added to C/C composites reacted with oxygen during ablation,and the generated ZrO2could block the infiltration of oxygen and reduce the ablation effect.Compared with other high temperature resistant ceramics(such as HfC and TaC),ZrC has lower density,which makes it easier to meet the requirements of lightweight in aerospace field.The differences in preparation process and ablation mechanism of ultra-high temperature ceramic modified C/C composites (C/C-UHTCs) are summarized,which can provide reference for other researchers in subsequent process and performance optimization[11].

Due to the long manufacturing cycle and high cost of C/C composites,some scholars use analytical method to calculate the equivalent thermal properties of composites,but this method requires different calculation models for different microstructures [12,13].At present,no analytical model can be applied to all composite microstructures.With the continuous development of C/C composites,the complexity of its microstructure is gradually increasing,and the difficulty of constructing analytical models is rising linearly,so it is necessary to carry out numerical analysis on the composites.The difficulty of numerical analysis lies in the establishment of finite element model.In order to consider the influence of pore defects in the matrix on the prediction of material properties,some scholars[14] established the prediction models of fiber size and fiber bundle size based on the asymptotic homogenization method,and calculated the equivalent thermal conductivity taking into account the pore defects.The results show that the randomness of pore distribution has little effect on the equivalent thermal conductivity of materials,but the volume fraction of pores has a significant effect on the equivalent thermal conductivity tensor,which decreases linearly with its volume fraction.In addition,the volume fraction of pores occurring in the matrix is more significant than that in the fiber reinforcement.Asymptotic homogenization method has a strict mathematical foundation,and the development of finite element method is mature.Combining the two methods can simplify the difficulty of programming by asymptotic homogenization method,and can also make use of rich finite element software library for prediction.Siddgonde et al.[15]used the representative volume element method,multi-scale modeling technology and the implementation of periodic boundary conditions to study the thermo-mechanical properties of two carbon/carbon 3D fabric composites,which was consistent with the experimental results.Dutra et al.[16]introduced in detail all the necessary steps to realize asymptotic homogenization by using ABAQUS software.The periodic boundary conditions that are not directly applied in ABAQUS software are described.It also describes the calculation of required data from the software output file and the calculation of homogenization matrix.The expansion equation of stress obtained by finite element commercial software at micro level is given in detail,and the necessary key points are given.Tian et al.[17] introduced the periodic boundary condition and its numerical realization algorithm in finite element software in order to obtain the equivalent mechanical properties of complex microstructure composites.In the commercial finite element software Abaqus,the effective mechanical properties of composite materials with complex microstructure are modeled by Python interface,periodic boundary conditions are imposed,and the average stress and strain are calculated.The numerical results show that the implementation algorithm in the finite element software proposed in this paper ensures the stress-strain continuity and uniaxial deformation constraint of the complex microstructure RVE of composite materials.Compared with Halpin-Tsai model and MT/Voigt homogenization method,the results show that the finite element homogenization method based on RVE can more accurately predict the effective elastic characteristics and elastic-plastic response of complex microstructure composites under the condition of imposing periodic boundaries.Using this method,the efficiency of performance calculation using asymptotic homogenization method is greatly improved,but the premise is to establish an appropriate finite element model.Most of the models established by existing numerical analysis only have fiber reinforced phase and matrix[18],and the inclusion phase is not taken into account.However,because the distribution of inclusions in the matrix is complex and changeable,simply treating them as homogeneous materials will bring new errors.Most fibers are represented by cylinders or hexahedrons[19,20],which can appropriately represent the fibers with tiled structure,but the braided structure will bring abnormal grids.Most scholars choose to divide the bending parts of fiber weaving with smaller scale grids to ensure the calculation accuracy.

In this paper,Gaussian random field method and threshold segmentation algorithm are adopted,and the finite element model of C-ZrC two-phase random particle reinforced microstructure is established by controlling the volume fraction and statistical characteristics of the reinforced phase.Then,the plain fiber structure is established according to the fiber linear equation,and the plain fiber structure is merged with the above-mentioned microstructure finite element model,thus the finite element model of C/C-ZrC is established.Based on the above C/C-ZrC composite model,the equivalent thermal conductivity tensor of C/C-ZrC composite is predicted by numerical asymptotic homogenization method.The influence of fiber volume fraction and ZrC volume fraction on performance prediction was explored.

2 Asymptotic Homogenization Expansion

2.1 Equivalent Thermal Conductivity Tensor

Zhang et al.[21] have expanded the equivalent heat transfer coefficient by asymptotic homogenization.In a three-dimensional simply connected region with infinite smooth boundary,the heat flux tensorqiis expressed as:

whereκijis the thermal conductivity tensor,Tis the temperature field,and the boundary conditions ‖qini‖=0 are supplemented,where‖P‖represents the discontinuity ofP.The macroscopic behavior of the structure can be expressed in the form of the following boundary value problem:

There are q(x,y)=0,y=x/εon the boundary.According to the chain rule,the derivative of the field variable with respect to the macro coordinate can be obtained:

The temperature field is asymptotically expanded by using the small parameterε,and the following results are obtained:

Similarly,the derivative expansion of heat flow can be obtained:

Substituting Eqs.(4)and(5)into Eq.(1),the asymptotic expansion of heat flow can be obtained:

Combining Eqs.(5)and(3),we can get:

Arrange the Eq.(7)according to the order ofε:

Forn=0,Eq.(10)turns:

For Eq.(6),when n=0 or 1,we can get:

Combine Eqs.(12)and(10),one can get:

According to Eq.(14),the relationship betweenT(1)andT(0)is expressed by the following formula:

Substituting Eq.(15)into Eq.(12)can get the relationship betweenq(0)andT(0):

Substitute Eq.(16)into Eq.(11),and take the average cell volume:

The equivalent thermal conductivity tensor is described as:

whereΘi(y)is the eigen temperature field.

2.2 Finite Element Implementation of AHM

Eq.(18) is the prediction formula of equivalent thermal conductivity based on asymptotic homogenization method.When using the above formula to predict the equivalent performance,only the eigen temperature fieldΘi(y)needs to be determined.Eq.(18)is transformed as follows:

whereθi0lrepresents the unit temperature gradient field,and in the three-dimensional problem,the unit temperature field is as follows,and the superscriptklrepresents the load condition,usually 11,22 and 33:

Applying the characteristic temperature fieldΘ*(kl)expressed by Eq.(20) to the finite element model,and adding the periodic boundary conditions,the solution can be obtained:

whereKis the thermal conductivity matrix andfis the corresponding heat flow load.

The thermal conductivity matrix is expressed as:

where[Ke]is the thermal conductivity matrix of the element and [B]is the generalized displacementstrain matrix of the temperature field.

The heat flow load is expressed as:

whereθ0(kl)represents the unit initial temperature gradient field.

Combine the matrix form of Eqs.(19)and(23),we can get:

2.3 Realization Method

To more clearly demonstrate the finite element software implementation of the Asymptotic Homogenization Method (AHM) in predicting the elastic constants of composites,we provide a detailed description of these processes below:

Step 1: Construct three node temperature fieldθ0(kl).Apply node temperature field on RVE and solve to get node heat flow loadf0(kl)for each condition.

Step 2:Apply node reaction field and periodic boundary conditions on the original RVE.Apply a fixed constraint to one vertex of the model.Then solve to obtain the eigen temperature t fieldθ*(kl).

Step 3:Apply the eigen temperature field on the original RVE and solve to obtain nodal heat flow loadf*(kl)corresponding to the eigen temperature fieldθ*(kl).

Step 4:Calculate the elastic constants from Eq.(24).

3 Construction of RVE Model for C/C-ZrC Composites

This part provides a detailed description of the generation process of the RVE model of C/C-ZrC.The first step is to use the Gaussian random field method to generate a three-dimensional grayscale model that maintains consistent grayscale values at the boundary to satisfy the periodic boundary conditions.Next,the grayscale model is segmented using the threshold segmentation method to generate a two-phase interleaved three-dimensional model.Finally,the material properties of the corresponding units are modified to complete the addition of the fiber structure by determining the location of the fibers.

3.1 Construction of RVE for Two-Inclusion Composites

3.1.1GenerationofGrayscaleModelsUsingGaussianRandomFunctions

The finite element model can be discretized into multiple elements,each of which can be considered as a pixel with an integer value called a gray level.Thus,the 3D model can be regarded as a spatially distributed field of random variables.In the Cartesian coordinate system,anm×n×l3D image can be represented as:

One of the critical statistical functions that characterizes the random field is the correlation function[22],which is an essential parameter to describe the stochastic medium.

lx,ly,andlzare the correlation lengths(Lc).The power spectral density functionMis as follows:

The Gaussian correlation function can be transformed by discrete Fourier transform to obtain the gray model,f(x,y,z),in three-dimensional space.

where

here,j,kandldenote the cumulative number of Gaussian correlation functions,i.e.,Gaussian complexity (Mn);Kxj,Kyk,Kzlare discrete sets of spatial frequencies;F(Kxj,Kyk,Kzl) is the power spectrum of a random process;andN(0,1)is a series of normally distributed numbers with a mean of 0 and a standard deviation of 1 in the range[0,1].

It is important to note that the gray random distribution model has several parameters,some of which impact the morphology of the non-uniform two-phase microscopic model.These parameters include correlation lengthLc,equally spaced dispersion pointsS,and Gaussian complexityMn.When using single-threshold partitioning to obtain a two-phase non-uniform microscopic model from the random gray distribution model,it naturally satisfies the periodic boundary conditions.The correlation length is linked to the continuity of the inclusion material,while the number of discrete points determines the smoothness of the model.Furthermore,the Gaussian complexity is associated with the randomness of the material distribution.

3.1.2ThresholdSegmentationofGrayModel

To obtain the two-phase model,an image segmentation algorithm is used to separate the target phase from the background matrix.The first step is to convert the gray model into a binary model containing only black and white pixels by threshold segmentation.Then,the phase volume fraction of the target component in the binary model is adjusted to the target volume fraction by adjusting the threshold size.

The binary model is obtained by normalizing the grayscale random distribution model,and the functionf(x,y,z)is in the range[0,1]:

wherefminandfmaxare the minimum and maximum values off(x,y,z).

The material propertyA(x,y,z)at a location in the unit is defined as:

whereA(j)represents the material properties of phasejandf0is the threshold value.The key to the threshold segmentation method is to determine the threshold that determines whether the volume fraction of the target phase of the binary model obtained is consistent with the expected volume fraction of the target model.

3.2 Construction of RVE Model for C/C-ZrC Composites

To add the fiber structure to the model,the material type of the unit at the corresponding position needs to be modified.This involves determining the position of the unit within the entire model.If the unit position meets the requirements,the material type of the corresponding unit is changed to fiber.

Fiber cross-sections are typically elliptical or rectangular.The parameters of the fiber crosssections are calculated based on the known material density of the composite and the material parameters of each constituent material.For instance,to obtain the appropriate major and minor axes for an elliptical section.The central line equation of the fiber is as follows:adjacent fibers of the plain structure are half a period apart.

Through a Fortran program,the position of the fiber is first screened.Ifx1andx2are the range of the fiber structure,when the coordinatexnof a node meetsx1＜xn＜x2,the coordinateynof this position is substituted into Eq.(31),and the center of the elliptical section of the fiber (xn,yn,zn) is calculated.Next,we put thexnandzncoordinates of any point and the central coordinates(xn,zn)of the ellipse circle into the ellipse equation set according to the fiber section to determine whether the point is within the ellipse range.If all the above conditions are met,the unit material type containing this node is modified to carbon fiber.According to the above method,the addition of the fiber phase in two-phase materials can be completed by setting different fiber curves at different positions and calculating the elliptical section center at corresponding positions.To modify the fiber shape or fiber spacing,only the parameters of the triangular function in the fiber curve need to be adjusted.

Using this approach,a three-phase microstructure with zirconium carbide,graphite,and carbon fiber was developed,and the results are shown in Fig.1.The model shown in the figure is the result shown in ANSYS.In this model,the volume fraction of zirconium carbide(blue)is 29.05%,the volume fraction of graphite(yellow)is 23.97%,and the volume fraction of carbon fiber(green)is 46.98%.

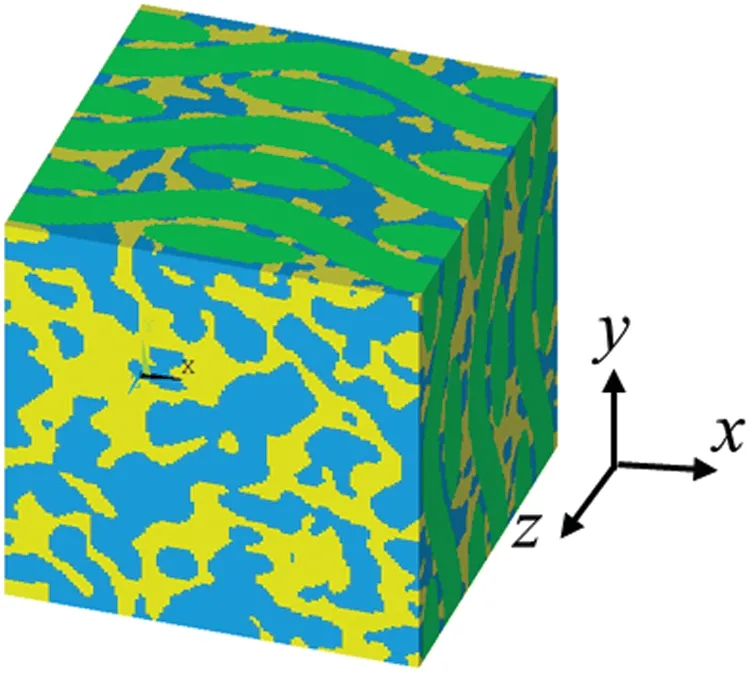
Figure 1 :Construction of C/C-ZrC model

This model was used to investigate the effect of microstructure on the properties of three-phase materials.Because the fiber is added by directly modifying the material properties of the element based on the inclusion model,the volume fraction of the final composite model is calculated by the following formula.When generating the inclusion model,the matrix generated under appropriate Gaussian complexity has high randomness.Therefore,when adding fibers,the volume fractions of different components are affected and changed together.

where,represents the volume fraction of ZrC in the inclusion model,represents the volume fraction of ZrC in the composite model,andrepresents the volume fraction of carbon fiber in the composite model.

4 Numerical Results and Discussion

The material parameters used in the calculation process are listed in Table 1.

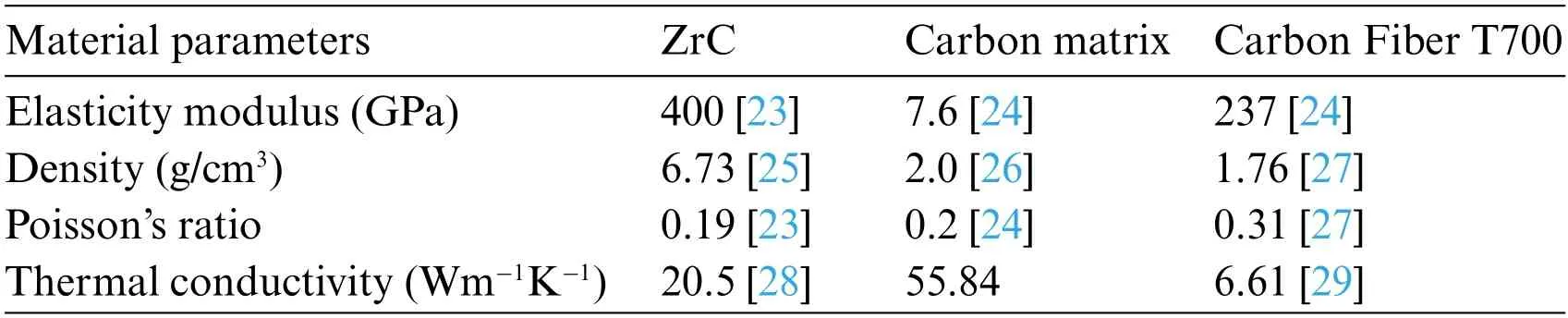
Table 1 : The material parameters

Among them,the thermal conductivity of carbon matrix was measured by Shanghai Institute of Silicate,China Academy of Sciences.The test basis was ASTM E1461-13,TA DLF-2800,ASTM E1269-18,Setaram MHTC96,the loading rate was 5K/min,and the atmosphere protective gas was Ar.

In this part,we primarily explore the effects of ZrC volume fraction,carbon fiber volume fraction,S,Lc,andMnon the performance.The proportion of ZrC volume fraction in the matrix changes from 0% to 100%.The carbon fiber volume fraction is controlled by different fiber layers,and the correctness of the model is verified.The fiber ply direction is defined as direction 1 and direction 2,and the direction perpendicular to the fiber ply is defined as 3.

4.1 Determination of RVE Parameters

4.1.1InfluenceofRVESizeonCalculationResults

The size of RVE will affect the calculation accuracy,so it is necessary to discuss the influence of the current RVE size on the simulation results and its influence law.In this section,the model shown in Fig.2 is taken as the basic unit.To discuss the influence of different RVE sizes on the calculation results,the unit model is expanded in the plane direction and vertical direction of fiber ply to generate RVE models with different sizes.Among them,the weaving structure of fibers determines the basic unit size of C/C composites,and the basic unit must contain the smallest periodic structure of fibers.

In this section,C/C-ZrC composites with 47vol.% carbon fiber and 26vol.% ZrC are selected to carry out sensitivity analysis of RVE size.The fiber volume fraction of 47vol.% determines that a basic unit contains at least three layers of fiber structure.In order to ensure the repeatability of fiber structure,the basic unit size of fiber is the minimum period length(LR)of fiber(see Fig.2).

The size of the fiber model is influenced by the fiber volume fraction,fiber density,and fiber section size.When the fiber volume fraction in the material changes,the size of the representative volume protocells needs to be recalculated to ensure a non-overlapping structure and repeatable periodicity between fibers.For C/C-ZrC composites,the representative protocell size is determined by the volume fraction of carbon fiber.

Figure 2 :Basic unit of RVE for calculation(model I)

Finally,according to the volume fraction of carbon fiber(47%),the typical cell sizeLRof C/C-ZrC composites is 1.53 mm×1.53 mm×1.53 mm,the fiber spacingwis 0.765 mm,the fiber cross section is oval,the ratio of long axis to short axisris 3.165,and the length of short semi-axisbis 0.09 mm.

When the size of RVE is enlarged,the basic cell is enlarged by cell replication to ensure the periodicity of surface mesh.In Table 2,models I～IV are respectively 1～4 times the extension ofLpin the fiber laying direction(x).In Table 3,models V～VII simulate the expansion of 2～4 timesLpin the direction perpendicular to the fiber laying direction(z).

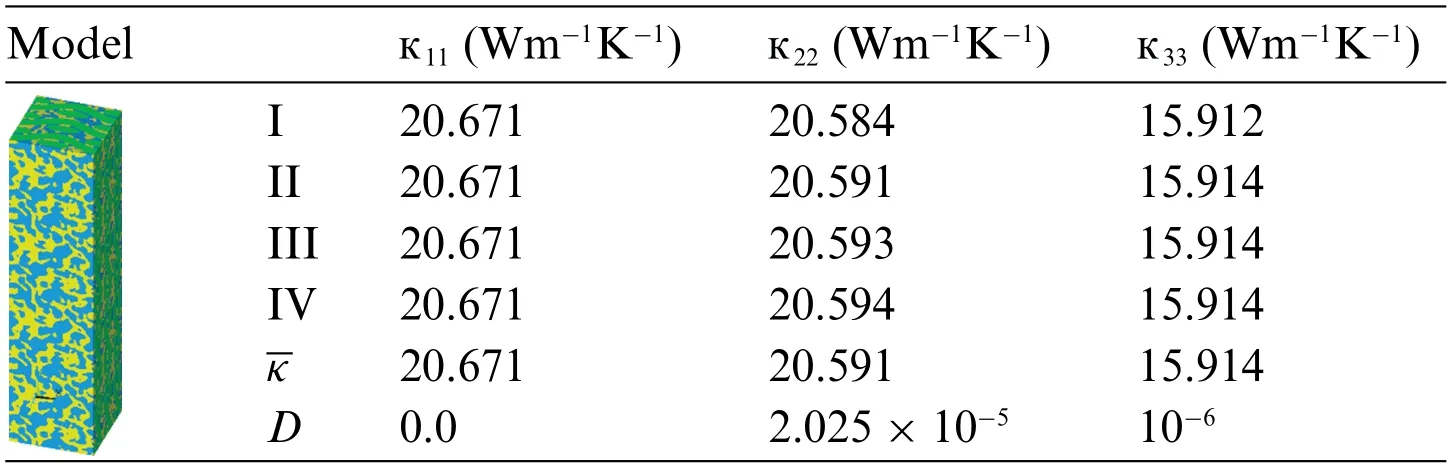
Table 2 : Thermal conductivity tensor of the model extending along the fiber laying direction

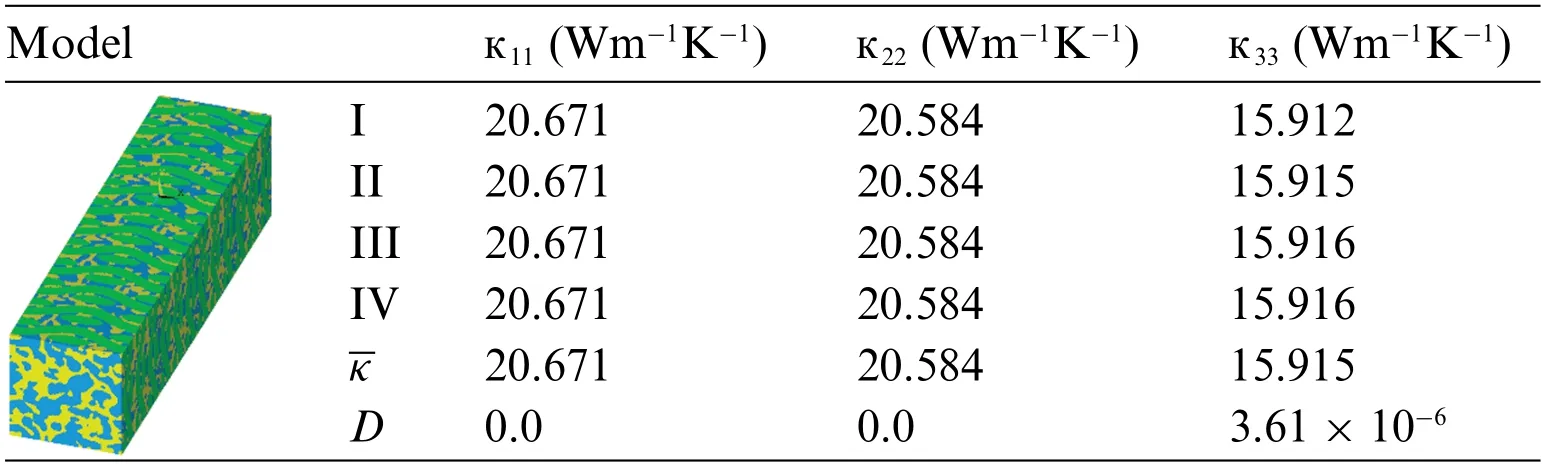
Table 3 : Thermal conductivity tensor of models extending in the vertical fiber laying direction

Statistical parameters(average and variance)are used to reflect the discrete amplitude of data.is the average of thermal conductivity tensor.Dpresents the variance.

where N is the number of samples.

Although the change of RVE size in two directions has an influence on the calculation results,compared with the average value,the maximum difference of equivalent thermal conductivity tensor component appears in22of model I,and the relative error is 1.18%.By comparison,whether the number of basic units is increased in thexorzdirection or in the three directions at the same time,it has little effect on the equivalent thermal conductivity tensor,and the calculation result of choosing model I as the basic unit is reliable.Considering the calculation accuracy and cost,the model with lengthLpcan meet various needs of mechanical properties calculation,so the RVE model shown in Fig.2 is used.

4.1.2SensitivityofMeshSize

The influence of the number of discrete points on the prediction of material properties is explored.The number of discrete points in a certain direction is taken as the number of cells in that direction,and four models with the same material composition but different cell numbers are established to study the sensitivity of mesh size.The cell sizeLRis 1.53 mm × 1.53 mm × 1.53 mm,the fiber spacingwis 0.765 mm,the fiber cross section is oval,the ratio of major axis to minor axisris 3.165,and the minor axis lengthbis 0.09 mm,47vol.% carbon fiber and 30vol.% ZrC(Lc=2.0,Mn=30).Due to the change of mesh size,the volume fraction of each model material fluctuates slightly.

By comparing the calculation results of different discrete points (Fig.3),it is found that the material properties fluctuate greatly when the mesh size is small(S＜40),and the calculation results are close to convergence whenS=50.

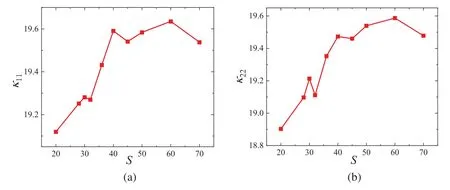
Figure 3 : (Continued)

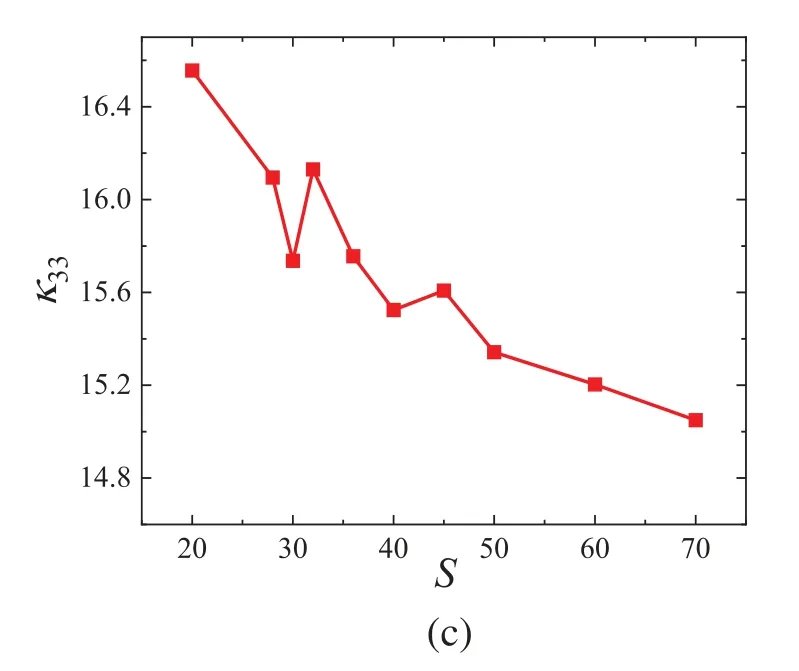
Figure 3 :Variation of thermal conductivity with discrete points(S)

4.1.3RelationshipbetweenGaussianComplexityandThermalConductivityTensor

To study the influence of ZrC distribution on the thermal conductivity of materials,Mn was changed from 10 to 150,and the particle size was kept constant.At this time,the correlation lengthLc=2.0,the number of equidistant discrete pointsS=50,the volume fraction of ZrC is 10%,the cell sizeLRis 1.53 mm,the fiber spacingwis 0.765 mm,the fiber cross section is oval,the ratio of major axis to minor axisris 3.165,and the length of minor axisbis 0.09 mm,so as to make an image of thermal conductivity aboutMn.The variance statistics of equivalent thermal conductivity obtained under each different Gaussian complexity are arranged in Fig.4.

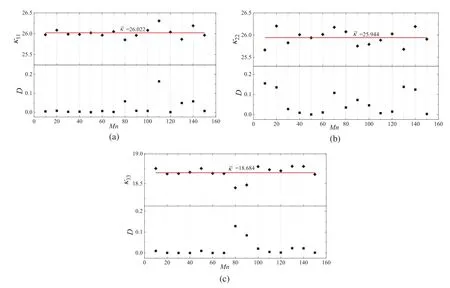
Figure 4 :Thermal conductivity tensor with different Gaussian complexity

As can be seen from Fig.4,the equivalent thermal conductivity of the material fluctuates up and down around the mean value,with a small fluctuation range,and the maximum error from the mean value is 1.37%.This shows that the thermal conductivity of composites fluctuates under different Gaussian complexity,but the fluctuation is very small,which proves that the equivalent thermal conductivity tensor calculated by different Gaussian complexity has converged under this particle size.

4.1.4RelationshipbetweenCorrelationLengthandThermalConductivityTensor

Keep the volume fraction of ZrC constant at 10%,change the particle size,and take 0.25 as the gradient step to do the function of thermal conductivity with respect toLc.The influence of particle size on the thermal conductivity of materials was investigated.Currently,the Gaussian complexityMn=30,the number of equally spaced discrete pointsS=50,the cell sizeLR=1.53 mm,the fiber spacingw=0.765 mm,the fiber cross section is oval,the ratio of major axis to minor axisr=3.165 and the length of minor axisb=0.09 mm.

The change ofLcreflects the particle size change of the inclusion phase in the matrix.In Fig.5,22decreases to 26.044 Wm-1K-1and then gradually increases,while11and33both show a downward trend with the increase ofLc.This shows that the increase of ZrC particle size is helpful to improve the thermal insulation performance and make the material have better structural stability at high temperature.

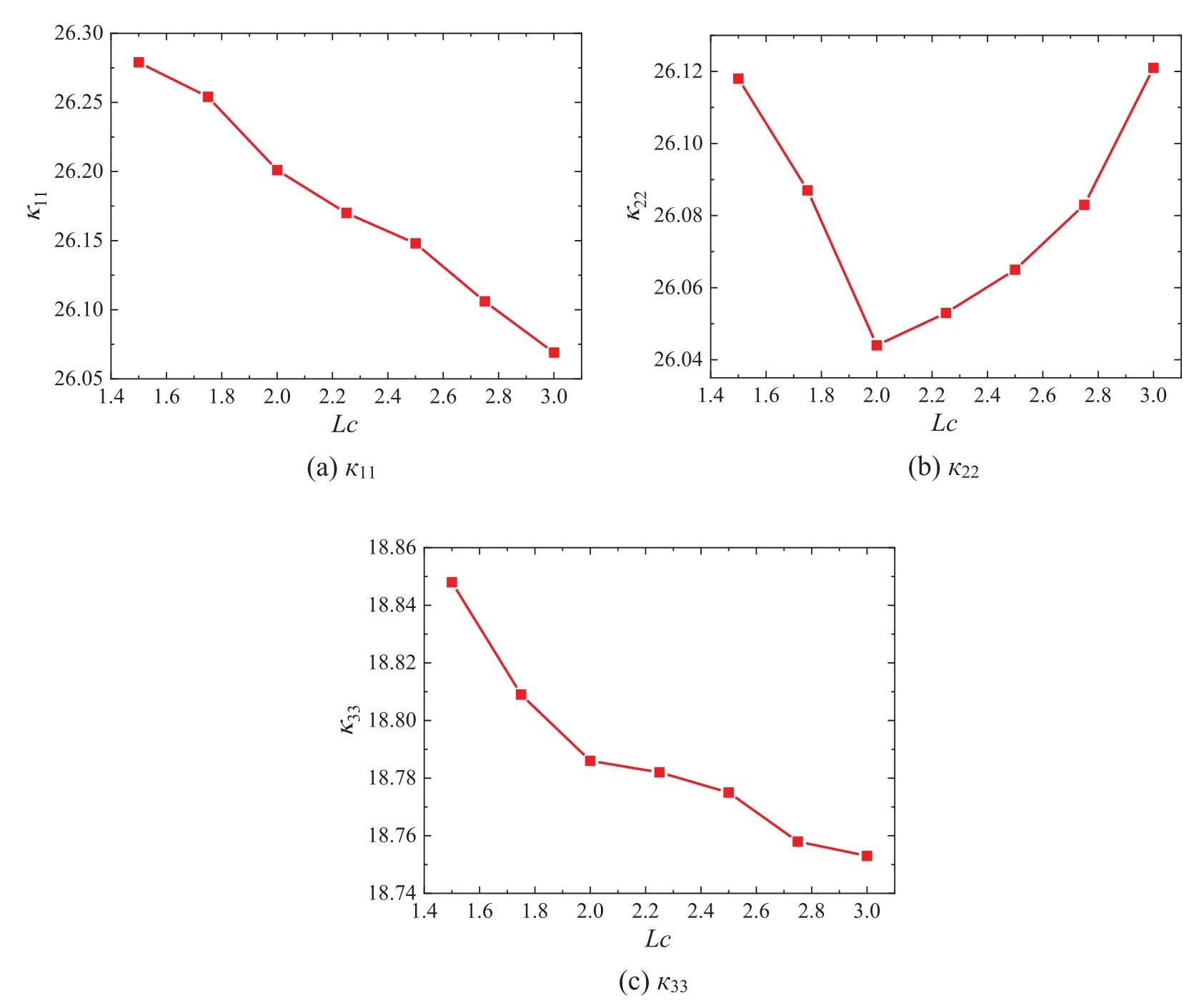
Figure 5 :Effect of correlation length on thermal conductivity

4.2 Effect of Fiber Gap on Thermal Conductivity Tensor

In the modeling method in this paper,to ensure the integrity of fiber structure,there is a gap between one fiber and another orthogonal fiber(as shown in Fig.6),andhCFrepresents the distance between the centers of two orthogonal fibers,that is,tin Eq.(31).

Figure 6 :Location of fiber gap(hCF)

This section mainly studies the composite material models with differenthCF,and explores the influence of the change ofhCFon the equivalent thermal conductivity tensor.By default,the value ofhCFis 0.25,the number of discrete pointsSis 50,the volume fraction of ZrC is 26.5%,the volume fraction of fiber is 47%,the correlation lengthLcis 2.0,and the Gaussian complexityMnis 300.In Fig.6,the short semi-axisbof the fiber is 0.08 mm,therratio of the long and short axes is 3.16,the original cell sizeLRis 1.53 mm,and the fiber spacingwis 0.765 mm.The influence of fiber spacing on thermal properties is explored.

The model of fiber gap increasing from 0.16 to 0.25 mm,fiber volume fraction of 47% and ZrC volume fraction of 26.5% was used to explore the changing law of thermal conductivity tensor.It is not difficult to see from Table 4 that11and22decrease gradually,while33increases gradually.Compared with the average value,11decreases by 1.0%,which shows that when the size of fiber gap increases gradually,the thermal conductivity in the thickness direction increases gradually,but the range of thermal conductivity change is not high.

4.3 Effect of ZrC Volume Fraction on Thermal Conductivity Tensor

The finite element model of thermal analysis is established by increasing ZrC at equal intervals of 0%～53%.Fig.7 shows the change of thermal conductivity with ZrC content.It is not difficult to see from the table that when the volume fraction of ZrC is 0.0%,11=30.0 Wm-1K-1,which is 9.27 Wm-1K-1higher than33,which is caused by different structures in the thickness direction.When the volume fraction of ZrC accounts for 53% of the matrix,the gap between11and33is obviously reduced,which is due to the large difference in thermal conductivity between carbon matrix and ZrC.With the increase of ZrC volume fraction,the gap between matrix and fiber is reduced.The material structure is transversely isotropic,and the equivalent thermal conductivity tensors of11and22are always close in direction 1 and direction 2.The equivalent thermal conductivity of materials is negatively correlated with the volume fraction of ZrC,and the fiber ply direction is always greater than the direction perpendicular to the fiber ply.The thermal conductivity gradually decreases with the increase of ZrC volume fraction,showing a negative correlation,in which33and ZrC content change approximately linearly.This shows that the addition of ZrC reduces the thermal conductivity of the whole material and improves the thermal insulation performance of C/C-ZrC composites.

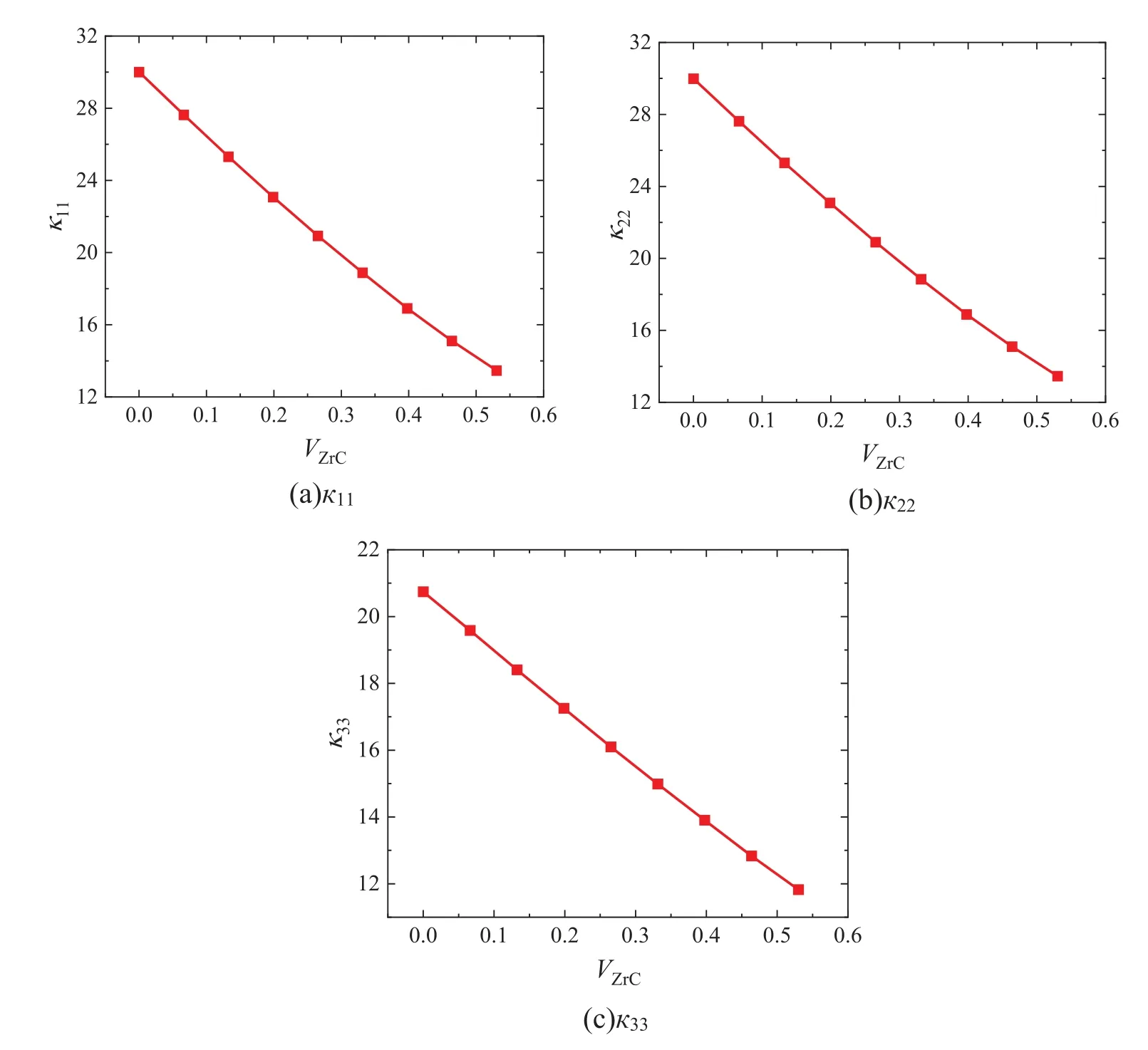
Figure 7 :Tensor component relation curve of ZrC volume fraction-thermal conductivity

4.4 Effect of Fiber Volume Fraction on Thermal Conductivity Tensor

To explode the influence of fiber volume fraction change on equivalent thermal conductivity tensor,a model is established according to the following parameters: ZrC volume fraction is kept constant at 30%,and when the number of fiber layers changes,the matrix is recalculated by Eq.(32)and generated.

As shown in Fig.8,it can be found that the values of11and22are close,and33is close to directions 1 and 2 when the fiber volume fraction is 0%.This is because the material currently is CZrC composite,and the value ofMnensures that the particles are sufficiently uniform in the matrix.At this time,the material can be regarded as isotropic,so the thermal conductivity in the three directions is close.

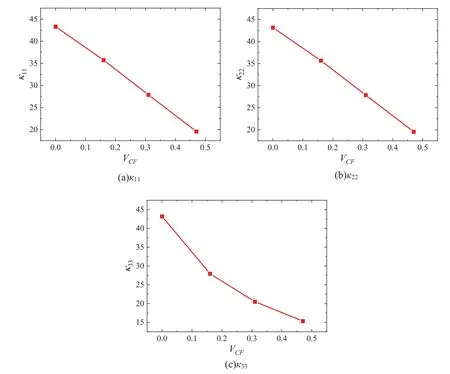
Figure 8 :Relationship curve between VCF and thermal conductivity tensor component

With the addition of carbon fiber,the equivalent thermal conductivity of the material shows a downward trend,and there is a linear downward trend between11and22and the volume fraction of carbon fiber.33is greatly influenced by the volume fraction of carbon fiber,and it can be obtained that the change of the volume fraction of carbon fiber mainly affects the thermal conductivity tensor component in the thickness direction.

5 Conclusion

In this paper,the finite element model of C/C-ZrC composites with random inclusion structure is generated by using Gaussian random field function,threshold segmentation method and fiber linear equation,and the thermal conductivity tensor is predicted by using this model.Gaussian random field function generates the original gray model with random distribution,and assigns a gray value to all pixels.Then,the threshold segmentation method is used to distinguish the two-phase materials,and finally the fiber structure is added according to the fiber linear equation.

The analysis and prediction results show that the fiber gap formed in the process of generating the model will not bring great fluctuation to the prediction results,but will only bring slight difference between the fiber ply direction and the vertical direction.Using this modeling method,the equivalent thermal conductivity tensor of C/C-ZrC composites is analyzed,and the relationship between fiber volume fraction and ZrC volume fraction and equivalent thermal conductivity tensor is explored.The main results are as follows: (1) The addition of ZrC enhances the thermal insulation performance.The larger the volume fraction of ZrC,the lower the equivalent thermal conductivity.When the volume fraction of ZrC increases from 0% to 26.5%,the tensor component11of equivalent thermal conductivity decreases by 30.24%.(2) There is a negative correlation between fiber content and thermal conductivity,and the addition of fiber improves the thermal insulation performance.When the fiber volume fraction is 47%,the equivalent thermal conductivity11is reduced by 23.725 Wm-1K-1compared with 0%.This is close to the law obtained by Pitchai et al.[30].It is proved that the finite element model generated by this method can be used to predict the properties of composites like C/CZrC.

Acknowledgement:Throughout the writing of this dissertation.I have received a great deal of support and assistance.I would first like to thank my supervisor,Lisheng Liu,whose expertise was invaluable in formulating the research questions and methodology.Your insightful feedback pushed me to sharpen my thinking and brought my work to a higher level.I would particularly like to acknowledge my group members,Liping Zu,for their wonderful collaboration and patient support.I would also like to thank my tutors,Hai Mei,Liangliang Chu,for their valuable guidance throughout my studies.You provided me with the tools that I needed to choose the right direction and successfully complete my dissertation.Finally,I would like to thank my parents for their wise counsel and sympathetic ear.

Funding Statement: Lisheng Liu acknowledges the support from the National Natural Science Foundation of China(No.11972267).

Author Contributions: Junpeng Lyu: Software,Validation,Formal analysis,Writing-original draft.Lisheng Liu:Conceptualization,Methodology,Supervision.Hai Mei:Validation,Supervision,Review&editing.Liping Zu:Formal analysis,Software.Liangliang Chu:Conceptualization,Methodology,Writing-review&editing.

Availability of Data and Materials: All data generated or analysed during this study are included in this published article.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.