Research and Application of a Multi-Field Co-Simulation Data Extraction Method Based on Adaptive Infinitesimal Element

Changfu Wan,Wenqiang Li,★,Sitong Ling,Yingdong Liu and Jiahao Chen

1School of Mechanical Engineering,Sichuan University,Chengdu,610065,China

2Innovation Method and Creative Design Key Laboratory of Sichuan Province,Sichuan University,Chengdu,610065,China

ABSTRACT

Regarding the spatial profile extraction method of a multi-field co-simulation dataset,different extraction directions,locations,and numbers of profiles will greatly affect the representativeness and integrity of data.In this study,a multi-field co-simulation data extraction method based on adaptive infinitesimal elements is proposed.The multifield co-simulation dataset based on related infinitesimal elements is constructed,and the candidate directions of data profile extraction undergo dimension reduction by principal component analysis to determine the direction of data extraction.Based on the fireworks algorithm,the data profile with optimal representativeness is searched adaptively in different data extraction intervals to realize the adaptive calculation of data extraction micro-step length.The multi-field co-simulation data extraction process based on adaptive microelement is established and applied to the data extraction process of the multi-field co-simulation dataset of the sintering furnace.Compared with traditional data extraction methods for multi-field co-simulation,the approximate model constructed by the data extracted from the proposed method has higher construction efficiency.Meanwhile,the relative maximum absolute error,root mean square error,and coefficient of determination of the approximation model are better than those of the approximation model constructed by the data extracted from traditional methods,indicating higher accuracy,it is verified that the proposed method demonstrates sound adaptability and extraction efficiency.

KEYWORDS

Multi-field co-simulation; adaptive infinitesimal elements; principal component analysis; fireworks algorithm;sintering furnace simulation

1 Introduction

With the continuous expansion of modern engineering system scales,excessive costs of physical experiments for complex engineering systems have become a significant limitation to developing innovative engineering designs [1–3].Through multi-field co-simulation based on the multi-field model,the coupling relations between parameters of each field can be fully taken into account and the simulation results of complex multi-field problems can be obtained[4].Predicting the structural life and reliability of complex engineering systems is gaining importance in the design process[5–7],yet complex engineering systems are usually under multiple physical field couplings.Hence,multifield co-simulation has become the main numerical simulation method utilized by researchers to solve complex engineering system problems in recent years [8,9].As the multi-field co-simulation dataset accommodates multiple physical field datasets in the same space and each field’s data is coupled and changeable,the multi-field co-simulation dataset demonstrates features of a large data amount and anisotropy in data distribution.Inappropriate data extraction methods will lead to low data extraction efficiency and affect the representativeness and complete distribution of data samples.Therefore,extracting field data samples with high representativeness and integrity from multi-field dataset with efficiency becomes the key technology to achieve multi-field co-simulation data post-processing.Zhou et al.used the multi-field co-simulation method with flow-thermal coupling to determine the flow field velocity and temperature field distribution of multiple profiles of the Nine-Spacer Nozzle structure[10].In [11],the motion process of the control rod driving mechanism in nuclear fuel assembly has been simulated utilizing the multi-field co-simulation method with the coupling of the motion field,electromagnetic field and flow field.The motion characteristics of the control rod driving mechanism and variation data of the flow field and electromagnetic field in the central profile have also been obtained from the simulation results.The multi-field co-simulation data extraction process of the control rod drive mechanism is also discussed in [12,13].The effect of pulse operation on the thermal stress response of virtual test blanket module has been examined by Ying et al.[14] using transient thermal-fluid-stress multi-field coupling analysis,and the simulation data of temperature field and thermal stress field on the outer surface and central profile of the structure have been obtained.A new flow field-thermal field-electric field multi-physical field numerical model was proposed in [15] to predict the performance of thermoelectric units for fluid waste heat recovery.The simulation results exhibit the temperature field distribution on the whole outer surface of the generator and transient electromagnetic furnace and the electric field voltage data on the upper surface of the transient electromagnetic furnace.A three-dimensional fluid-thermal-structural multi-physical interaction simulation model for aluminium extrusion process has been established by Maher et al.in[16].By coupling the simulation model with the structural mechanics analysis,the stress distribution in the die under fluid pressure and thermal load is simulated,and the full three-dimensional results in the processes of temperature distribution,velocity distribution,von Mose stress distribution,equivalent strain distribution and pressure distribution of selected profiles are provided and analyzed.In [17],the three-dimensional fluid-thermal-structural multi-field coupling analysis of the cooling sleeve of supersonic combustion ramjet (scramjet) engine has been performed to extract the data of flow field,temperature field and stress-strain field on the inner surface of the cooling channel,and to predict the structural life of the cooling sleeve.The interlaced fluid-solid coupling algorithm is used by Ko et al.[18] to simulate the internal and external flow field changes of a launch vehicle and demonstrate the flow field and temperature field in the central profile of the launch vehicle.Meanwhile,the unsteady motion of separated rocket booster is predicted using the external flow analysis of the pneumatic-dynamic coupling solver.The internal flow field of the umbrella wind turbine was simulated in[19],with the velocity field and pressure field data in profiles of 0°,45°and 60°shrinkage angles extracted,providing a theoretical basis for further improving the power regulation mechanism of umbrella wind turbines.Siregar et al.[20]conducted numerical simulation on the temperature field and flow field in inductively coupled thermal plasma(ICTP)extracting and displaying the temperature field in Z profile of plasma torch and discussed the effects of gas composition and power supply on the temperature field of thermal plasma.The operation of high temperature and high pressure furnace equipment was simulated in [21–25] via flow-thermal coupling multi-field co-simulation analysis,and the temperature fields and flow field distributions of multiple profiles of the furnace body have been extracted and displayed.To sum up,the research of multi-field co-simulation data extraction method has made positive progress.According to different application scenarios,a more reasonable spatial profile datasets extraction method is proposed,and partial data of multiple physical fields are obtained,which provides a basis for the optimization design of equipment structure.

At present,the data samples of multi-field co-simulation field are mainly extracted by selecting a single or multiple spatial profile datasets of field.Highly representative and complete simulation data samples will facilitate accurate reflection on the performance of complex engineering equipment,which helps the optimization on the structure of engineering equipment.However,large data amount and data distribution anisotropy of multi-field co-simulation dataset determines that the selection of direction,number and position of the profile will greatly affect the representativeness and integrity of field data sample extraction,and determines the efficiency of data extraction directly.Therefore,a multi-field co-simulation data extraction method based on adaptive infinitesimal elements is hereby proposed in this study.A multi-field co-simulation dataset has been constructed based on related infinitesimal elements,a characteristic direction determination method based on principal component analysis for effective determination of profile direction is introduced,and an adaptive micro-step length determination method based on fireworks algorithm to select appropriate number and position of profiles is expounded.The aforementioned address the two key techniques of data extraction.The method has also been applied to the data extraction process of multi-field co-simulation dataset of sintering furnace,and the results have been compared with traditional data extraction methods to verify the rationality and effectiveness of the proposed method.

2 Multi-Field Co-Simulation Data Extraction Method Based on Infinitesimal Element Method

Multi-field co-simulation dataset,as a continuous dataset composed of complex multi-physical fields distributed along the simulation space,has the characteristics of large data amount and anisotropy in data distribution.In case only a few feature profile datasets are extracted from a multifield co-simulation dataset,the data samples would be too small to represent the characteristics of multi-field data; yet if too much data is extracted,excessive representation of field data sets will also affect the extraction efficiency.Additionally,unreasonable selection of profile direction will damage the distribution integrity and representativeness of data samples as well.In this study,the correlation between adjacent profile datasets is analyzed by the infinitesimal element method,and the representative profile datasets are extracted to express the distribution characteristics of multi-field dataset.The principal component analysis method is used to determine the direction of profile and the firework algorithm is used to calculate the micro-step length adaptively.

2.1 Construction of Multi-Field Co-Simulation Dataset Based on Related Micro-Element

Due to the coupling effect of multi-physical fields in the simulation process,the multi-field cosimulation dataset comes with the characteristic of multi-field data coupling,as well as complex and changeable data field in the same space.Therefore,the multi-field co-simulation dataset can be established using the same reference frame in the same simulation space.In accordance with the continuity of multi-field data,m profile micro-datasets(data infinitesimal elements)in any simulation direction space can be extracted from each physical field simulation dataset of the multi-field cosimulation dataset composed of S physical field couplings.The relations between each dataset are as follows:

where V is the same simulation space where multiple physical field reside;x,y and z are coordinates in the simulation space;FSis the multi-field co-simulation dataset;αs(x,y,z)are the continuous functions of each field dataset;andPb(x,y,z)are the continuous functions of the micro-dataset of each profile.If two data infinitesimal elements in the same physical field demonstrate low correlation,they will be regarded as unrelated,otherwise they will be considered repeating as related infinitesimal elements.The defined valueRABrepresents the correlation between the micro-datasets A and B,which can be calculated by the following formula[26]:

where X is the number of sampling points in each micro-dataset;αAiandαBiare the data of theith sampling point in data infinitesimal elements A and B,respectively;andare the average values of the sampled data in data infinitesimal elements A and B,respectively.

To extract representative and complete samples of multi-field dataset,a multi-field co-simulation data sample extraction model based on the concept of infinitesimal element has been proposed in the current study.Each physical field simulation dataset of a multi-field co-simulation dataset can be sliced into m profile micro-datasets in a certain direction,with the direction of micro-datasets segmentation defined as the characteristic direction →Lof simulation dataset,and the interval along the characteristic direction between the two profile micro-datasets is defined as micro-step length ΔL.Along the characteristic direction,the two adjacent infinitesimal elements A and B are defined as neighborhood datasets,and the two micro-datasets in each neighborhood dataset are sampled successively.The correlation between them is calculated to identify the relations between them.The correlation threshold of micro-datasets R is defined as: if |RAB|＞R,the two datasets are regarded as related,then one of them will be eliminated;if not,both will be retained and the samples of each physical field simulation datasets composed of several profile micro-datasets will be obtained.At last,to form the multiple field co-simulation dataset samples are formed via coupling of each physical field simulation dataset sample in the same simulation space.The details are shown in Fig.1.

To facilitate the extraction of multi-field co-simulation data samples,two key technical problems are crucial:the selection of data infinitesimal elements’characteristic direction and the determination of micro-step length of data infinitesimal elements.Firstly,as the spatial characteristics of multi-field co-simulation dataset are different,different data infinitesimal elements will be obtained from slicing along different characteristic directions.Also,different characteristic directions will have a significant impact on the simulation data extraction results.Secondly,extraction data with different micro-step length will lead to different data processing quantities and data extraction accuracy,which will greatly affect the reliability of data extraction results.

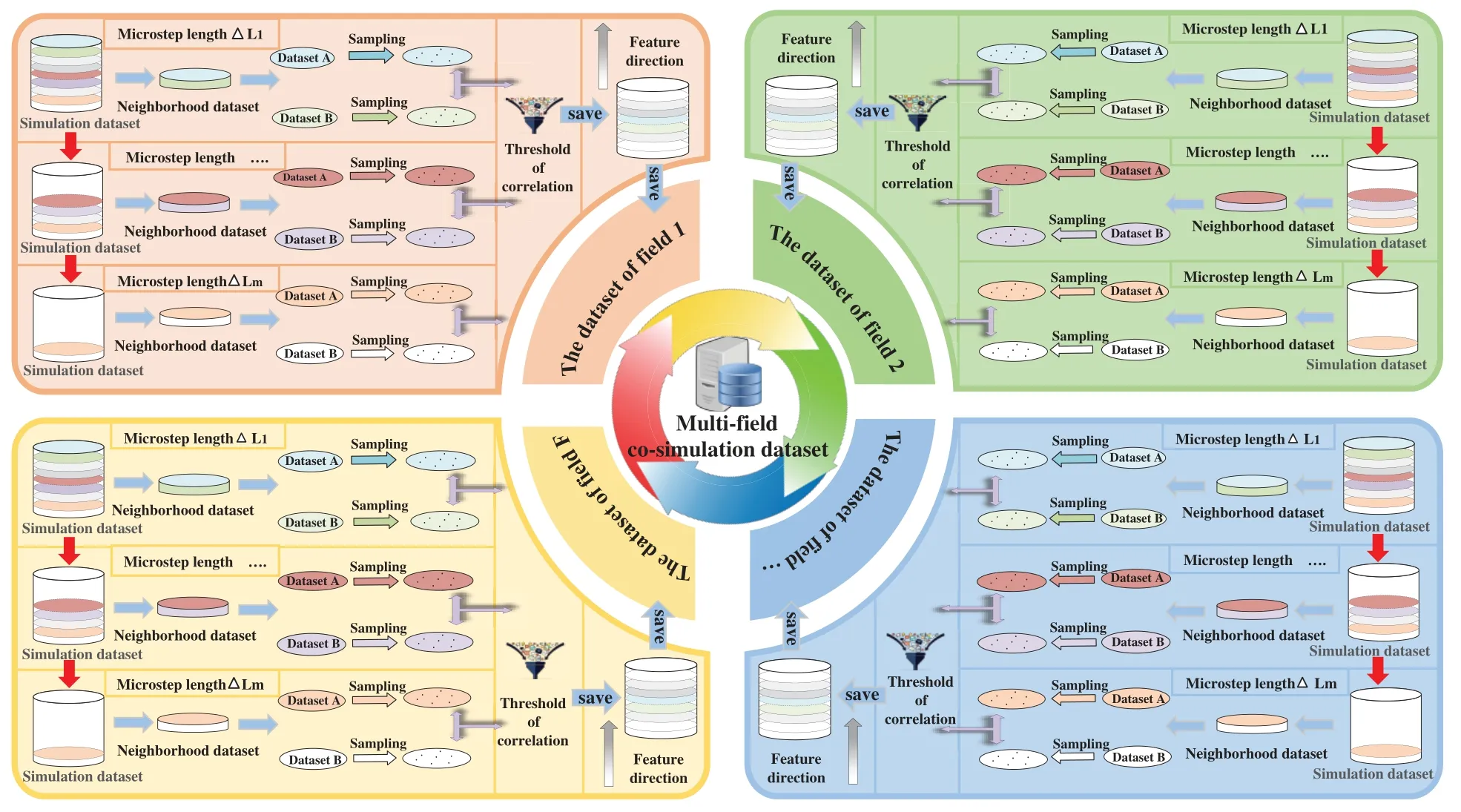
Figure 1 :Multi-field co-simulation data extraction model based on related infinitesimal elements

2.2 Determination Method of the Characteristic Direction for Data Extraction

When the micro-step length approaches infinitesimal,two profile micro-datasets in the neighborhood dataset can be considered to be fully correlated.However,the micro-step length cannot approach infinitesimal in reality and if there is an angle between the spatial surface of the simulation dataset and the selected characteristic direction,a ladder effect will occur between the two profile micro-datasets in the neighborhood dataset,leading to different data sampling area of the two profile micro-datasets and ultimately the error of correlation calculation.This error is hereby defined as the correlation error E,as shown in Fig.2.Therefore,it is similar to the determination of printing direction in additive manufacturing [27,28]: when the spatial surface of the simulation dataset has been determined,the selection of characteristic direction should reduce the correlation error E of data extraction as much as possible.

From the analysis,when the selected characteristic direction is parallel or perpendicular to the simulation dataset surface,the correlation error caused by the ladder effect can be minimized.Hence,all the surface unit normal vectorsof the dataset can be selected as the candidate characteristic direction set(for curved surfaces,directions with the smallest correlation errors and different from the normal directions of other flat surfaces are selected as candidate directions),and the correlation error in each candidate’s characteristic direction can be calculated,respectively.The unit normal vector with the minimal correlation error is selected as the final characteristic direction,and the formula for calculating the correlation error E is as follows:

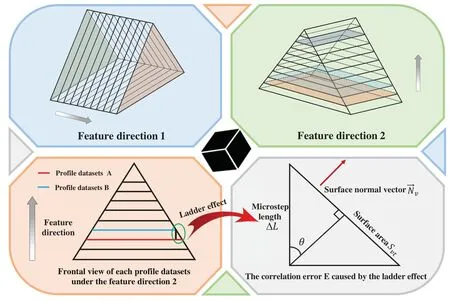
Figure 2 :Effects of different characteristic directions and ladder effects on the same spatial simulation dataset

Calculating the correlation errors with the unit normal vector of each surface as the characteristic direction successively will lead to large calculation amount,therefore dimension reduction of the candidate characteristic direction setis necessary,via reducing the number of candidate characteristic directions.Principal component analysis (PCA) [29,30] is a common statistical method,which can transform multiple initial variables into a small number of comprehensive variables (i.e.,principal components)by linear transformation.The principal components are not related with each other and are able to reflect most of the information of the initial variables with no redundancy.The unit normal vectorof each surface in the dataset can be obtained by establishing the coordinate system in the three-dimensional space of the dataset.From the above analysis,it can be seen that the correlation error is not only related to the direction of each surface,but also to the surface area.Yet,the surface unit normal vectoronly represents the direction,therefore,the surface unit normal vectorcan be weighted by the surface areaSwof each surface,and the area-weighted normal vectorwhich can characterize both direction and surface area is obtained:

In which,the sample space of the new area-weighted normal vector isSince the characteristic direction(unit normal vector)sample space only contains x,y and z coordinate information,principal component analysis is performed on this sample space,with a corresponding covariance matrix(3×3)constructed and singular value decomposition carried out.Three eigenvectors are obtained,which contain the most information of the sample space.Hence,they are eligible to be deployed as candidate characteristic directions after dimension reduction.

First,the average normal vectorof n area-weighted normal vectors is calculated:

The difference between each area-weighted normal vector and the average normal vector is calculated,and the difference value vectoris obtained:

Construct a covariance matrixC=

Given that the covariance matrix C is a real symmetric matrix,the Jacobi SVD method can be utilized to decompose the covariance matrix C via singular value decomposition.Three eigenvalues and their corresponding eigenvectors can be obtained,from which the direction with the smallest correlation error can be selected and determined as the final candidate characteristic direction.

2.3 Determination Method of Microstep Length for Adaptive Data Extraction

The selection of micro-step length ΔLhas a great impact on the data processing amount and the accuracy of related infinitesimal element data screening.When the micro-step length ΔLapproaches infinitesimal,more related infinitesimal elements can be screened out and more profile datasets can be extracted in data extraction,yet result in a sharp increase in the amount of data processing and calculation simutaneously.In contrast,when the micro-step length ΔLbecomes larger,although the data amount to be processed will be reduced,it will lead to a significant loss of representative simulation data.In this study,a smaller micro-step length has been applied in the part of the simulation dataset with a stronger data variation trend,and larger micro-step length is used to extract the data in the part with a smaller data variation trend.A determination method of micro-step length based on the fireworks algorithm(FWA)[31]for adaptive data extraction is proposed.

The fireworks algorithm,a global optimization algorithm,simulates the phenomenon of fireworks explosion to conduct global search [32].Fig.3 is the optimization framework of the fireworks algorithm.In this study,the fireworks algorithm is deployed in segmented intervals in search of the optimal data extraction positions,so as to determine the micro-step length.To begin,the initial profile micro-dataset A is set up and the interval of the next extraction interval to be optimized is calculated.The fitness functionf(xi)is the absolute value|RAB|of the correlation coefficient between the initial profile micro-dataset A and the next extracted profile micro-dataset B.The smaller the absolute value|RAB|of the correlation coefficient,the higher the fitness of the next extracted profile micro-dataset B.The specific definition off(xi)is as follows:

In which,X is the number of sampling points in each micro-dataset;αAiandαBiare the data of theith sampling point in the initial profile micro-dataset A and the next extracted profile micro-dataset B,respectively;andandare the average values of the sampled data in the initial profile micro-dataset A and the next extracted profile micro-dataset B,respectively.

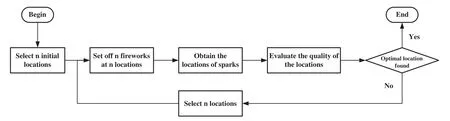
Figure 3 :Optimization framework of fireworks algorithm

The optimal termination condition is set as when the number of iterationsT＞Tmax.For the initial optimization,T=0,and the maximum number of iterationsTmaxis determined according to the amount of extraction data and accuracy.The specific flow of the determination method of microstep length based on the fireworks algorithm for adaptive data extraction is as follows:

Initialize data extraction parameters:the initial profile micro-dataset A is determined;taking the characteristic direction as the coordinate axis and the position of micro-dataset A in the characteristic direction as the origin to establish a single-dimensional coordinate system;ΔIi+1is set as the value of the next extraction interval length,ΔIiis set as the value of the extraction interval length being optimized,ΔI1is set as the value of the interval length of initial optimization,andTmaxis set as the maximum value of iterations;the interval to be optimized is set asLi=in which i represents theith interval optimized by FWA.In particular,L1=[0,ΔI1],xiintis the coordinate position of the extracted profile micro-dataset obtained from the final optimization of the previous optimization interval.is defined as the optimal fitness value obtained in theith interval optimized by FWA.

Determine the data interval L to be optimized,and set the initial position point:if i=1,then L=Li=L1,and n points are set initially in the optimization interval with number of initial iterations T=0,andR1wait=1.If i ＞1,then L=Li.The length ΔIi+1of the next extraction interval to be optimized is calculated,and n points are initially set in the interval to be optimized with the number of initial iterations T=0,and=1.

Based on the above,to address the selection of different micro-step lengths in different regions of the simulation dataset,an adaptive adjustment coefficient S is introduced in the current study.It is able to adaptively adjust the range of interval to be optimized according to the data characteristics of different areas,improving the search efficiency of FWA optimization,finding out the position of data extraction profile as soon as possible,so as to determine the micro-step length ΔL.The formula for calculating the adaptive adjustment coefficient S is as follows:

k(k ＞0)is the slope trend factor that can change the adjustment amplitude of S.It is determined according to the spatial range and data extraction accuracy of the simulation dataset.INT is defined as a rounding function to ensure that the length of the optimization interval is an integer.RABis the optimal fitness value(correlation coefficient)selected in the current optimization interval and meets the requirements 0 ≤|RAB|≤1.When:|RAB|=0.5 and S=1,the interval length does not change;RAB＞0.5 and S ＞1,the data information in the interval to be optimized demonstrates duplication.is at a larger value under this condition,and the range of the next optimization interval can be increased rapidly;RAB＜0.5 and S＜1,the data information in the interval to be optimized demonstrates minor duplication.is at a relatively smaller value,and the range of the next optimization interval can be reduced slowly.Additionally,the limitεL≤ΔIi+1≤μLis set,withεLandμLas the maximum and minimum limits to prevent local mutation of micro-step length.Both shall be determined by the simulation space range and optimization accuracy.

Decide the termination condition of data sample extraction:in case the extraction interval is beyond the scope of the simulation dataset space,data sample extraction of dataset shall be terminated.Otherwise,it shall be continued.

Fireworks algorithm optimization:n fireworks are placed at n fireworks placement points in the interval to be optimized.The fitness of each fireworkf(xi),the number of explosion sparksSiand the explosion radiusAiare calculated.The specific formulas are as follows:

In which,xi(i=1,2,...,n)is the position coordinate of theith firework;f(xi)is theith(i=1,2,...,n)fitness value of firework;Max[f(xi)]is the maximum fitness value among all fireworks;m is the parameter to control the number of sparks generated by fireworks;εis the minimum value to avoid irrational formula;INT is defined as a rounding function to ensure the number of sparks is an integer.

In which,Min[f(xi)] is the minimum fitness of all fireworks,andis the maximum explosion range of fireworks.

Based on the mapping rule,the positionxji(j=1,2,...,Si)of the explosion spark caused by theith fireworks is obtained,and the fitness function valueof each explosion spark is calculated.The specific mapping rules are as follows:

Initialize the location of the explosion spark:xji=xi

Setz=round(d·rand(0,1)),z ≥1;where d is the dimension of position coordinatexi,and rand(0,1) is a random number uniformly distributed over [0,1].Yet as d=1 has already been set in this study,z is identically equal to 1.

Hence,xji+1=xji±RandValu,RandValu=Ai·rand(0,1).

Thenxji+1will be mapped to the potential space,gettingin which % is the remainder function.

The minimumRABis selected fromand the fitness function values of all fireworks position pointsxiand explosive spark position pointsxji.Then letRAB=,the position point with the minimumRABis the candidate position point of this data extraction profile micro-dataset.

Decide the termination condition of optimization:decide whether the number of iterations T meets the optimal termination condition,i.e.,T≥Tmax.If satisfied,the position point ofRAB=shall be selected as the position of this data extraction profile micro-dataset,and the micro-step length of this interval is determined.Meanwhile,let i=i + 1 and calculate the next data interval to be optimized according to formulas(12)and(13),setting initial position point and continuing the fireworks algorithm optimization for micro-step length in the new data optimized interval.If not,proceed to the next step.

Screen the next generation fireworks:n next generation firework location points are set based on selection probabilityP(xi),making T=T+1.n fireworks are placed at n newly selected firework setting points,then perform a new round of fireworks algorithm optimization in the data interval to be optimized.The formula of selection probabilityP(xi)is as follows:

where K is a collection of all fireworks and exploding sparks.

3 Data Extraction Process of Multi-Field Co-Simulation Based on Adaptive Infinitesimal Elements

Based on the aforementioned determination methods for characteristic direction and micro-step length,a multi-field co-simulation data extraction process based on adaptive infinitesimal elements is hereby introduced,as shown in Fig.4.

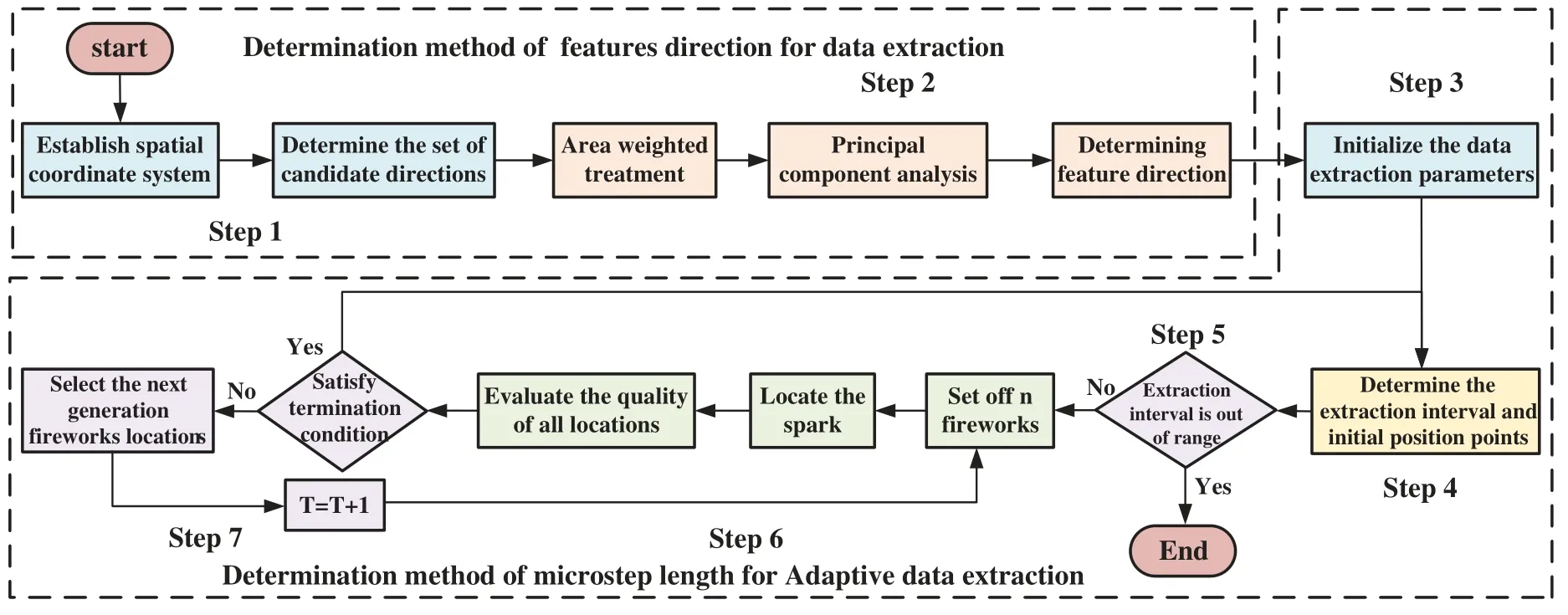
Figure 4 :Data extraction process of multi-field co-simulation based on adaptive infinitesimal elements

Step 1:create a candidate direction set.Establish the 3D spatial coordinate system of the simulation dataset,and the unit normal vectorsof all surfaces of the dataset are selected as the candidate characteristic direction set.

Step 2:determine the characteristic direction.Area weighted normal vector(w=1,2,...,n)is subjected to the principal component analysis.The correlation error E under the three candidate characteristic directions is calculated,and the characteristic direction with the smallest correlation error E is selected as the final characteristic direction.

Step 3:initialize the data extraction parameters.The initial profile micro-dataset A is determined.The single-dimensional coordinate system is established.The initial optimal interval length ΔI1and the optimal termination conditionsTmaxand other parameters,etc.,are set.

Step 4:determine the interval to be optimized.The range of extraction interval to be optimized is determined,and n fireworks position points are initially set in the interval to be optimized with initially settingR1wait=1.

Step 5: determine the termination conditions of data sample extraction.Determine whether the extraction interval to be optimized is beyond the scope of the simulation dataset.If so,end the extraction process,otherwise proceed to the next step.

Step 6: fireworks algorithm optimization.The fireworks are placed at the n selected fireworks location points,and the fitness values of the fireworks and spark are calculated.The smallest position point is selected from the fitness function value of all fireworks and explosion spark position points and compared with the value of.The minimumRABis selected from them,withRAB=The position point with the minimumRABis the candidate position point of this data extraction profile dataset.

Step 7:determine termination condition of optimization.Termination shall be subject to whether the number of iterations T meets the termination condition of optimizationT≥Tmax.If so,the position point ofis selected as the position of the current data extraction profile micro-dataset and return to Step 4 to complete the search for the next data extraction location.If not,the selection probability of all fireworks position pointsxi(i=1,2,...,n) and explosion spark position pointsxj(j=1,2,...,Si)shall be calculated to determine the position points of the next generation fireworks,with T=T+1,for continuing a new round of optimization.

4 Application

Pressure sintering furnace is a type of industrial equipment for sintering cemented carbides,as shown in Fig.5.Cemented carbide sintering contains a number of processes,such as hydrogen dewaxing,vacuum sintering,pressure sintering and pressure relief cooling.It is a typical coupling process of the flow field and thermal field with the control of temperature field in the sintering furnace exerting significant influence on the quality of sintered products.Due to factors as measured space and heat transfer conditions,direct multi-point temperature measurement in the furnace is not always feasible.Therefore,it is of great significance to examine the temperature field in the furnace by using simulation technology.In this study,the flow-thermal multi-field co-simulation of pressure sintering furnace in sintering process is carried out,and the simulation data are extracted by the proposed multifield co-simulation data extraction method in order to obtain the temperature field distribution pattern in the furnace efficiently.The atmosphere field(flow field)distribution pattern can be obtained in the same way.The two fields together constitute the pressure sintering furnace multi-field co-simulation dataset.

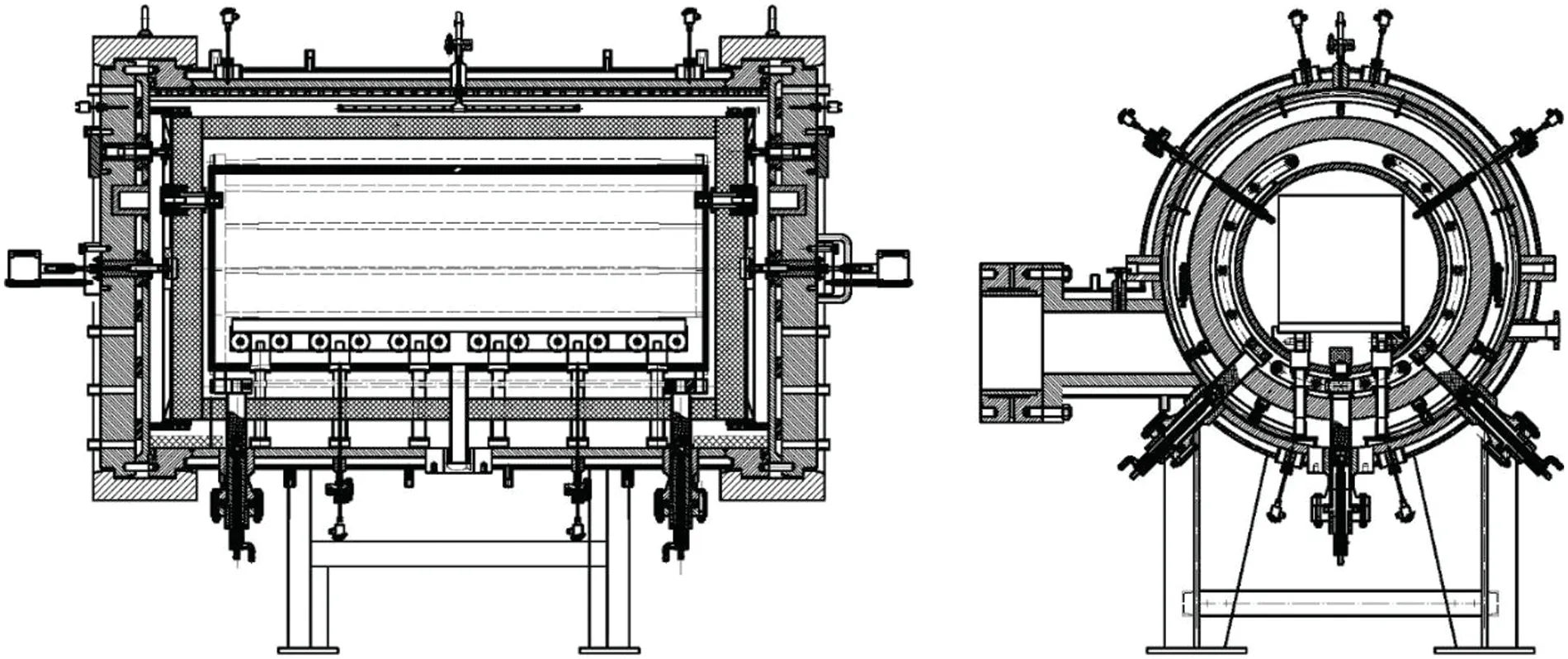
Figure 5 :Assembly drawing of a pressure sintering furnace

In this study,a simplified fluid domain model in sintering furnace has been established,as shown in Fig.6.In the stage of hydrogen dewaxing,the 14 heating rods are sparsely installed above and densely installed below,and the furnace is continuously heated to of process node temperature at a total power of 500 Kw.Hydrogen is induced at the rate of 0.85 m/s into the inlet to fill the space between the thermal insulation layer and the porous graphite layer,and the wax gas produced by dewaxing of the alloy and hydrogen is discharged through the lower outlet.

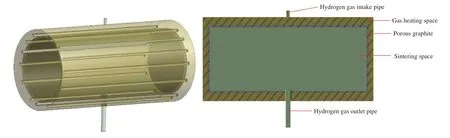
Figure 6 :Simplified fluid domain model of pressure sintering furnace

Set parameters and boundary conditions as shown in Tables 1 and 2.Establish fluid simulation model of sintering furnace based on the aforementioned working conditions,and the boundary of the model is shown in Fig.7.

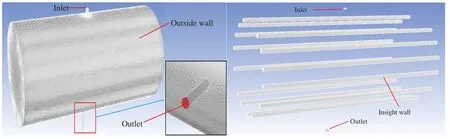
Figure 7 :Simulation model boundary of pressure sintering furnace

Based on the simulation model and parameter settings above,the simulation dataset of the sintering furnace is obtained via co-simulation of the flow field and thermal field.The convergent residual curve is obtained and the temperature nephogram,pressure nephogram and streamline diagram of the axial central profile of sintering furnace are extracted.As shown in Fig.8,the residual error of the model converges to 1e-3in 18186 steps;at this time,a temperature characteristic of colder in the upper part and hotter in the lower part of the furnace is demonstrated.

Figure 8 :Convergence process and results of pressure sintering furnace simulation

4.1 Sample Extraction Process of Representative Data in Sintering Furnace Simulation

When the temperature in the furnace reaches the temperature required by the process node,the cemented carbide being sintered will be gradually dewaxed to reduce its carbon content.At this point,the temperature distribution in the furnace has a great influence on the quality of cemented carbide dewaxing.In this study,the temperature field data in the furnace are obtained with the proposed data extraction method and process,and the specific process is as follows.

Step 1:Create a candidate direction set.The 3D spatial coordinate system is established by taking the spatial center point of the sintering furnace simulation dataset as the origin,and the candidate direction setis established as shown in Fig.9.Surface 4.1 and Surface 4.2 are two sides of the simulation dataset.Surface 7.1,Surface 7.2 and Surface 7.3 are annular walls of gas heating space,porous graphite and sintering space,respectively.Surface 2 is a typical cylindrical surface whose bus lines are parallel to the X-axis,so the spatial unit normal vector set of Surface 2 is a set of vectors that diverge along the plane parallel to the Y-Z plane.The unit normal vector with 45 degrees angle to the Y-axis,which is different from the normal vector direction of other surfaces,is selected as the candidate direction.

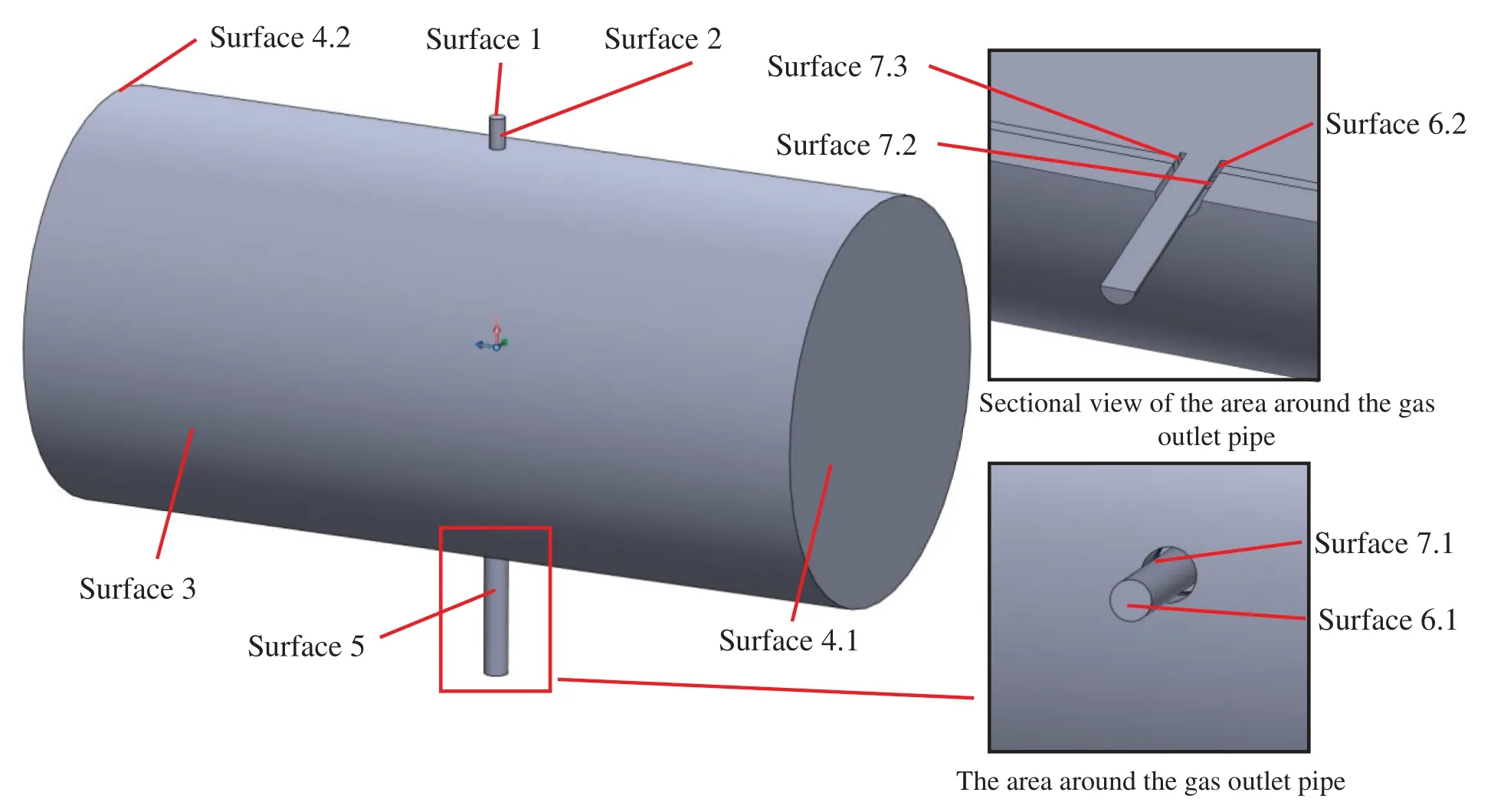
Figure 9 :Spatial surfaces of sintering furnace simulation dataset

Similarly,Surface 3,Surface 5 and Surface 7 can be established.Typical directions different from other surface normal vector directions can be selected from their respective spatial normal vector sets.All candidate directions are shown in Table 3.

Step 2: Determine the characteristic direction.The unit normal vector of each dataset surface obtained above is weighted by surface area to obtain the area-weighted normal vectorthat can characterize the direction and surface area simultaneously.The principal component analysis method is used for dimension reduction on the candidate direction set.7 average vectors of area-weighted normal vector=(0.023,99.337,12.726) have been obtained,and the difference value vectorbetween each area-weighted normal vector and average normal vector is obtained,as shown in Table 4.

According to formula(10),the covariance matrixC=can be constructed as:

The eigenvalues and eigenvectors of the covariance matrix C are calculated,the three main characteristic directions,and(i.e.,principal components) of the candidate characteristic direction set are obtained,which are the candidate characteristic directions,as well as the correlation error E in the three candidate characteristic directions.It can be seen from the analysis that the value of each correlation error E is the sum of the projected areas of each surface that will have ladder effect with the selected characteristic direction.The candidate’s characteristic directionwith correlation error E which is smaller than those ofandis selected as the final charactertistic direction,as shown in Table 5.

Step 3:Initialize the data extraction parameters.Given the similarity and universality in the process of determining data extraction micro-step length by fireworks algorithm optimization,only the first round optimization of fireworks algorithm optimization in the initial optimization interval is taken as an example to demonstrate the data extraction process.Set Surface 4 as the initial dataset A and take the characteristic directionas the coordinate axis and the position point of Surface 4 on the coordinate axis as the coordinate origin to establish a single dimensional coordinate system G.The unit length is 1 mm.It can be seen that the position coordinates of Surfaces 4.1 and 4.2 are 0 and 2140,respectively.Since the simulation data space is symmetric along the characteristic direction,the data extraction range is set as[0,1070].The temperature field near the initial region demonstrates significant variation,hence the length of the initial optimization interval has been set as 8 mm.The number of fireworks has been set as 7,and the maximum number of iterationsTmax=2 has been set.

In view of the difficulty in extracting all data point information from the profile micro-dataset,X data points evenly distributed in profile micro-dataset have been randomly selected to characterize the whole profile micro-dataset in the current study,as shown in Fig.10.To determine the reasonable number X of sampling points,two uniformly distributed profile micro-datasets have been randomly selected.The correlation R has been calculated according to the gradual change on the number of sampling points in Table 6.When the number of sampling points exceeds 600,the range of fluctuation between the correlations R of the two profile micro-datasets does not exceed 5%.It can be considered that the calculated correlation is independent from the number of sampling points.Hence the number X of sampling points of profile micro-datasets in the process of optimization can be set as 600.

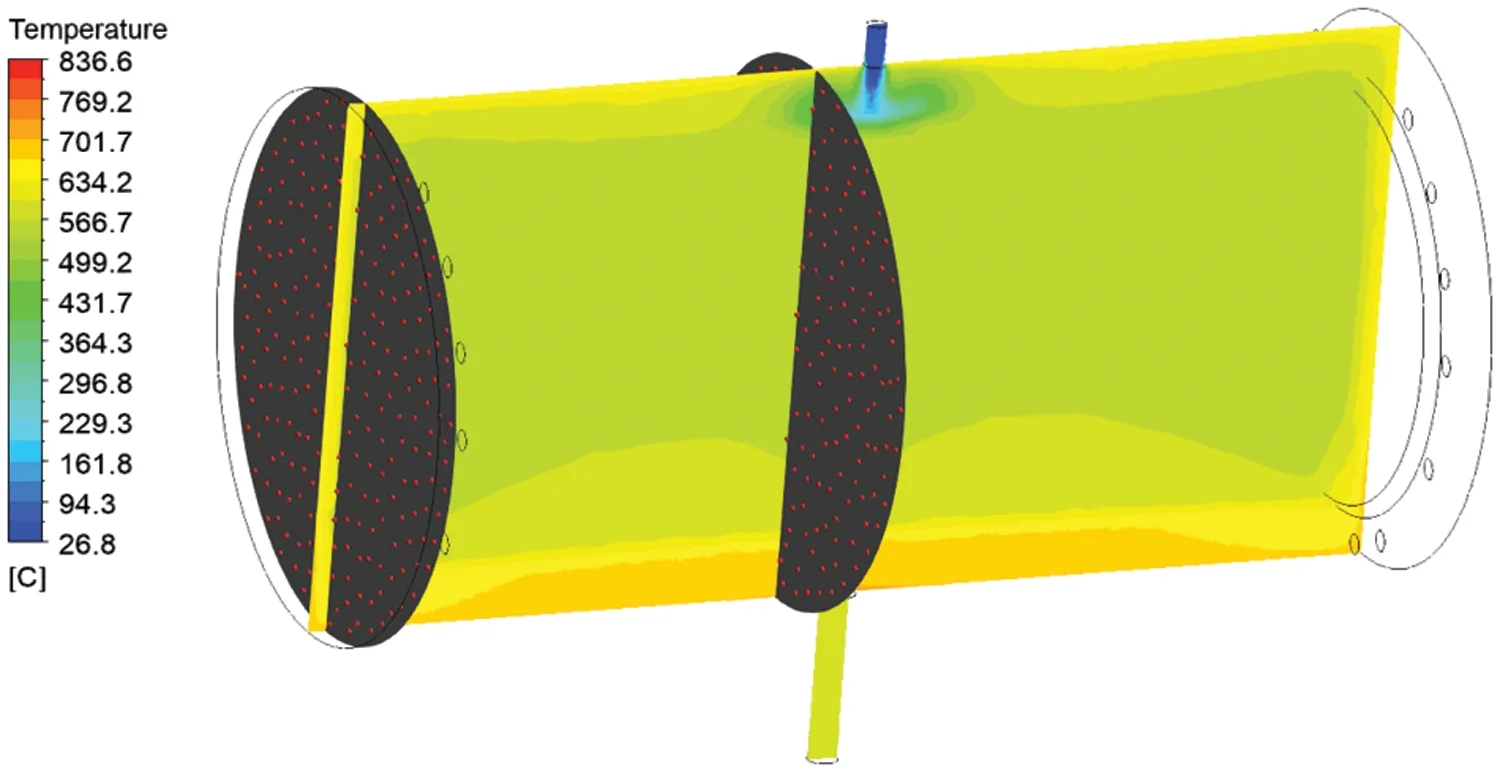
Figure 10 :Random sampling point distribution of profile micro-dataset

Step 4:Determine the interval to be optimized.The range of initial optimization interval is set as[0,8],All optimization intervals are subject to the same processing.The optimization interval is divided into eight equal parts,and the fireworks placement points are set to 1,2,3,4,5,6,and 7 mm,with initial settingR1wait=1.

Step 5:Determine the termination conditions of data sample extraction.As long as the spatial range of simulation dataset does not exceed the initial optimization interval,the optimization will continue.

Step 6:Fireworks algorithm optimization.The fitness functionf(xi)of 7 fireworks setting points in the initial optimization interval is calculated,as well as the number of explosion sparksSiand the explosion radiusAi.Considering the optimized interval length and fireworks number,the spark number parameter m=2(n+1)=16 and the maximum explosion amplitudehave been set.The details are shown in Table 7.

When the explosion parameters of each fireworks point are obtained,the specific position and fitness function valueof each explosion spark are calculated based on the mapping pattern,in whichRandValu=.The details are shown in Table 8.

The minimumRABis selected fromand the fitness function values of all fireworks position pointsxiand explosive spark position points.The position pointx25=5.2427 with the minimumRABis the candidate position point of the profile micro-dataset in this data extraction,then letRAB==0.0040.

Step 7: Determine the termination condition of optimization.As the number of iterations T=1＜Tmaxdoes not meet the optimization termination conditions,the optimization shall continue.The selection probabilityP(xi) of all fireworks and exploding sparks is calculated according to formulas(16)and(17),and the results are shown in Table 9.The 7 coordinate points with the highest selection probabilities are selected as setting points for the next generation fireworks,as shown in Table 10.Finally,let T=T+1,and reinitiate Step 6 for a new round of optimization.

Table 1 : Simulation model parameters

Table 2 : Boundary condition settings

Table 3 : Candidate characteristic directions set

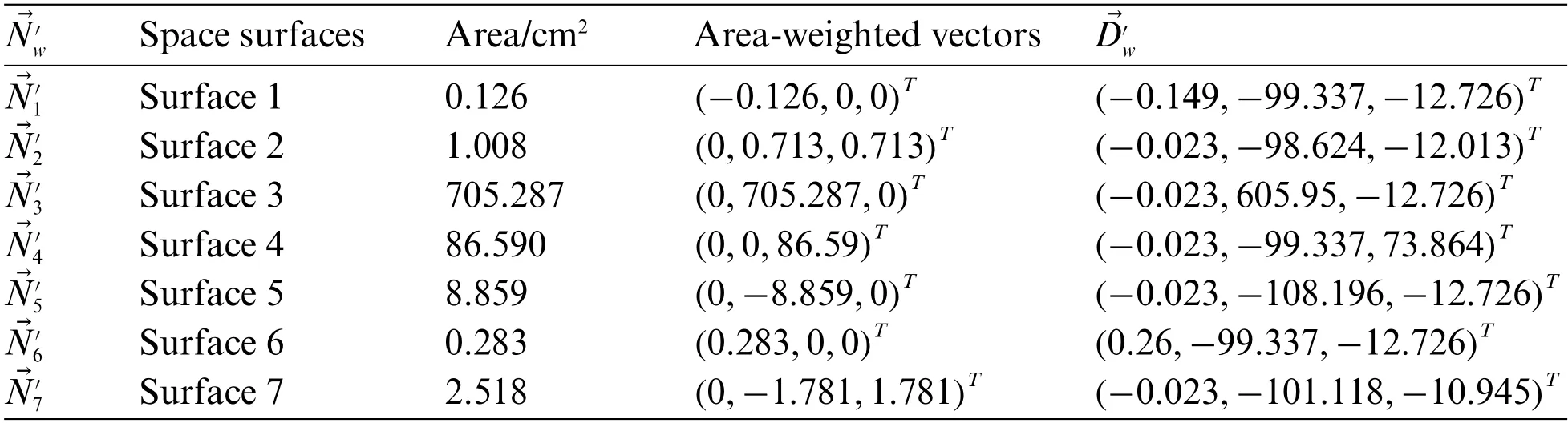
Table 4 : Dimension reduction process of the candidate direction set

Table 5 : Correlation error E of the final candidate characteristic direction

Table 6 : Number setting and correlation results of different samples

Table 7 : Fireworks explosion parameters at each point

Table 8 : Explosion spark parameters

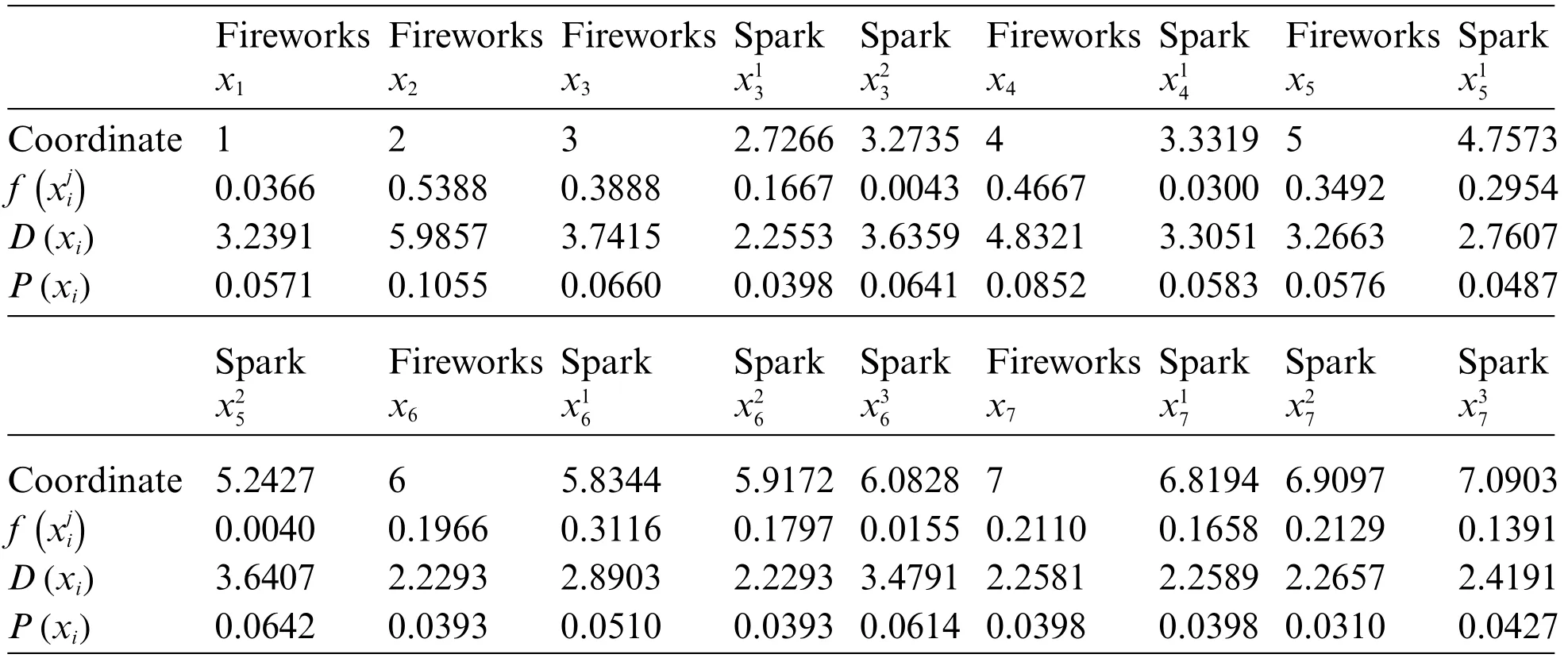
Table 9 : Explosion parameters and selection probability of fireworks and explosion sparks

Table 10 : The parameters of next generation fireworks setting points

After the setting points of the next generation fireworks are obtained,the optimization process of Step 6 is repeated.The minimumRAB=R1wait=0.0033 and the minimum position coordinate ofRAB=6.0950 are obtained.Repeat the determination process as in Step 7 with the optimization termination conditionT≥Tmaxat iteration number T=2.The coordinate position 6.0950 ofRAB=R1wait=0.0033 is determined as the final position point of data extraction in the initial optimization interval,with the micro-step length set as 6.0950.Then,reinitiate Step 4 for further optimization.The next interval to be optimized could be calculated based on formulas(12)and(13),with the slope trend factor k=1.5.From calculation ΔI2=3 can be obtained,hence the next optimization interval range is[6.095,9.095].Meanwhile,the maximum limit valueμL=107 and the minimum limit valueεL=1 are set.The rest of the process is repetitive and not detailed hereafter.

The last extraction interval to be optimized is determined as beyond the range of the sintering furnace simulation dataset and thus the data extraction process of the sintering furnace simulation data sample is considered completed.The final dataset samples of the sintering furnace simulation are shown in Table 11.The data samples are composed of 35 profile micro-datasets,each containing the coordinates and temperature information of 600 data points.To save space,Table 11 only exhibits part of the data samples.

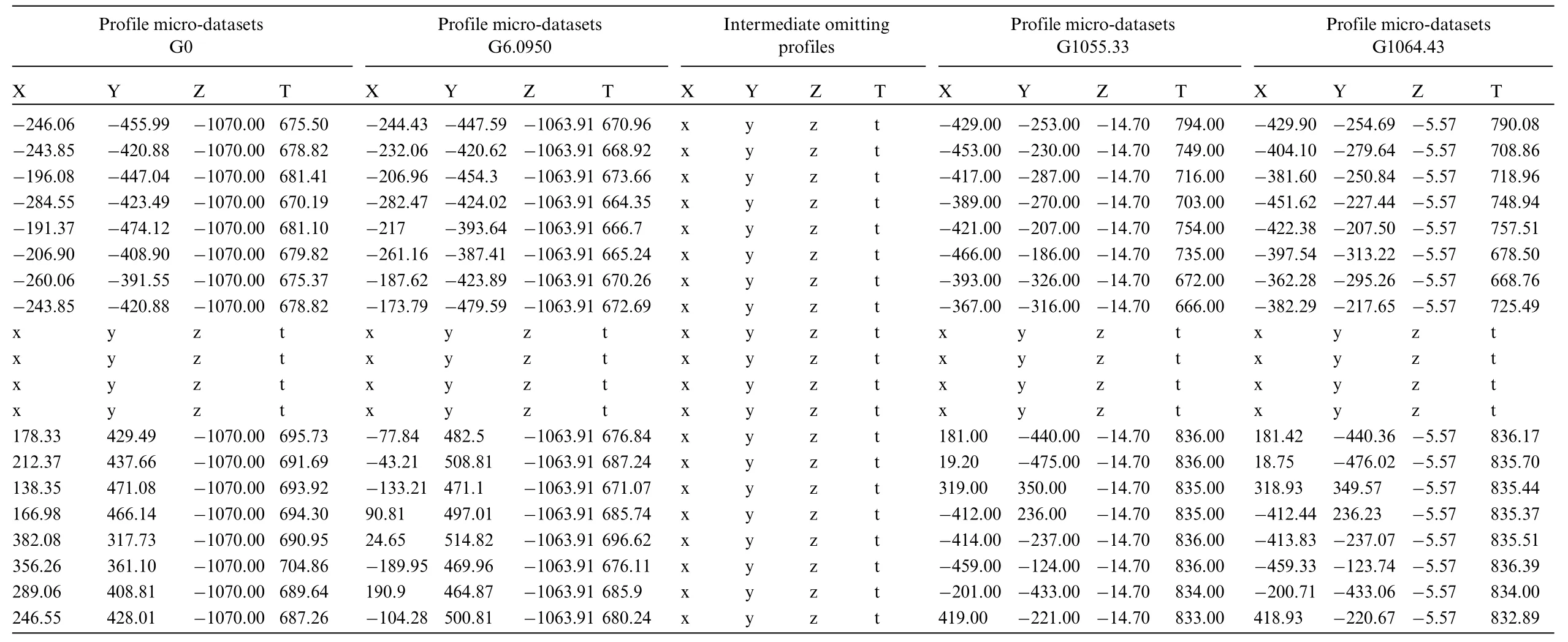
Table 11 : Data samples of sintering furnace simulation datasets

The variation trend of micro-step length along with sampling profile micro-datasets is showed in Fig.11.The initial sampling area of the sintering furnace dataset is near the furnace door,and the temperature field changes acutely,which leads to small micro-step length.Then the sampling gradually approaches the furnace body and the temperature field tends to be stable,resulting in gradual increase and stability of micro-step length.Finally,the sampling area is near the inlet,and micro-step length demonstrates a rapid decrease as a result of sharp change of the temperature field.By analysis,the variation of the micro-step length of the algorithm is consistent with that of the simulation temperature field,and the expected effect of data sampling has been achieved.

4.2 Validation of Data Samples

An accurate approximation model of the sintering furnace temperature field can be constructed with highly representative and complete simulation data samples.Deploying approximation model,a mathematical model meeting the accuracy and computational efficiency requirements based on limited experimental data can be constructed,which can be utilized to simulate the input-output relations of complex problems.Comparative studies on commonly-used approximation models have demonstrated that radial basis function neural network model has high prediction accuracy and robustness under large sample size,with high computational efficiency of model construction and prediction.It is applicable to highly nonlinear approximate problems with accuracy,and has been widely used in engineering product optimizations [33–35].In the current study,two radial basis function approximation models A1and A2of sintering furnace temperature field have been constructed based on the data samples extracted by the method proposed in this study and the conventional data extraction method,respectively.The accuracy of each approximate model has also been examined to demonstrate the effectiveness of the sintering furnace simulation data samples extracted by the method proposed in this study and further verify the rationality and reliability of the proposed method.

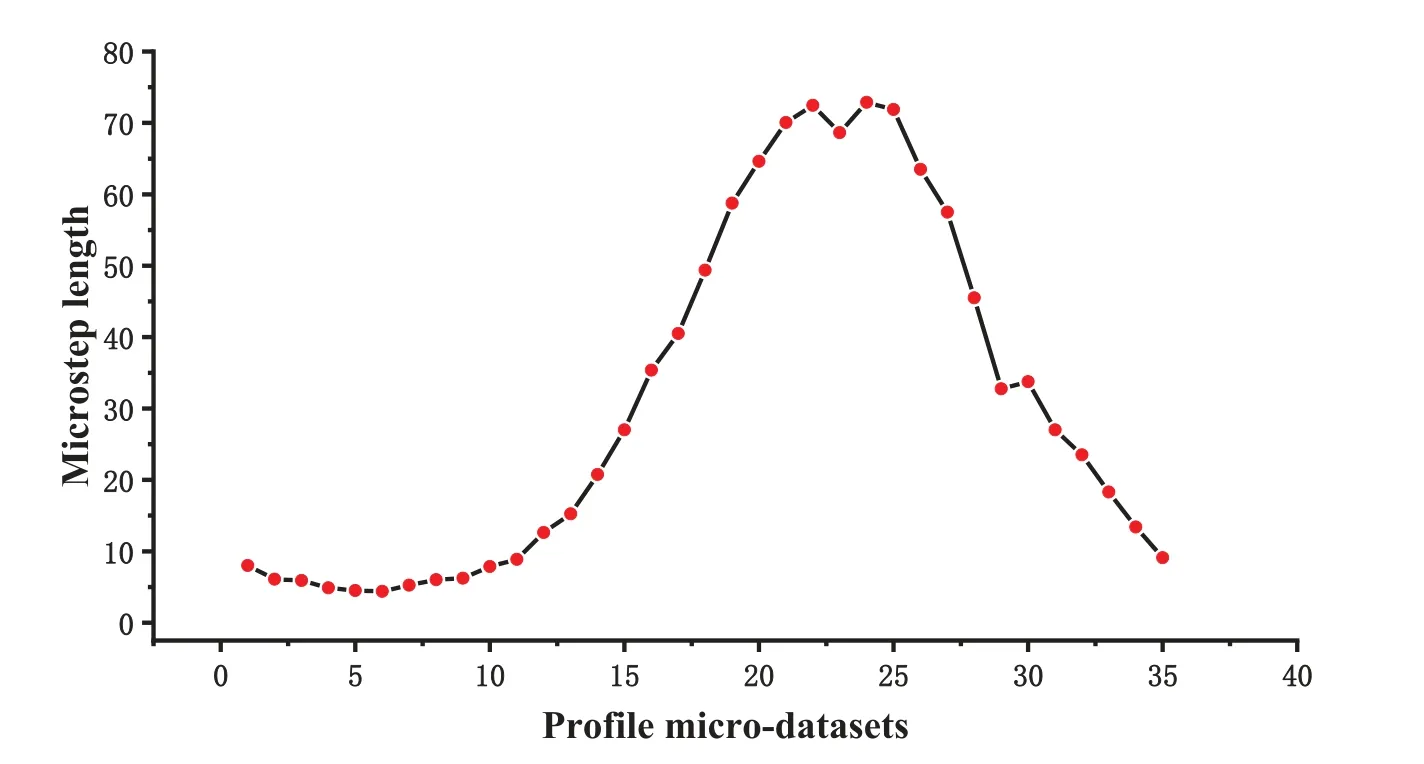
Figure 11 :Trend of micro-step length changing with sampling profile micro-datasets

Conventional multi-field co-simulation data extraction methods mainly rely on the selection of multiple equal-distance spatial profiles of field dataset to extract the simulation data sample.The simulation datasets control samples extracted in this fashion are shown in Table 12.The data samples are composed of 43 profile micro-datasets.The distance between each profile micro-datasets is 25 mm,and each profile micro-datasets also contains the coordinate and temperature information of 600 data points.To save space,Table 12 only demonstrates part of the data samples.

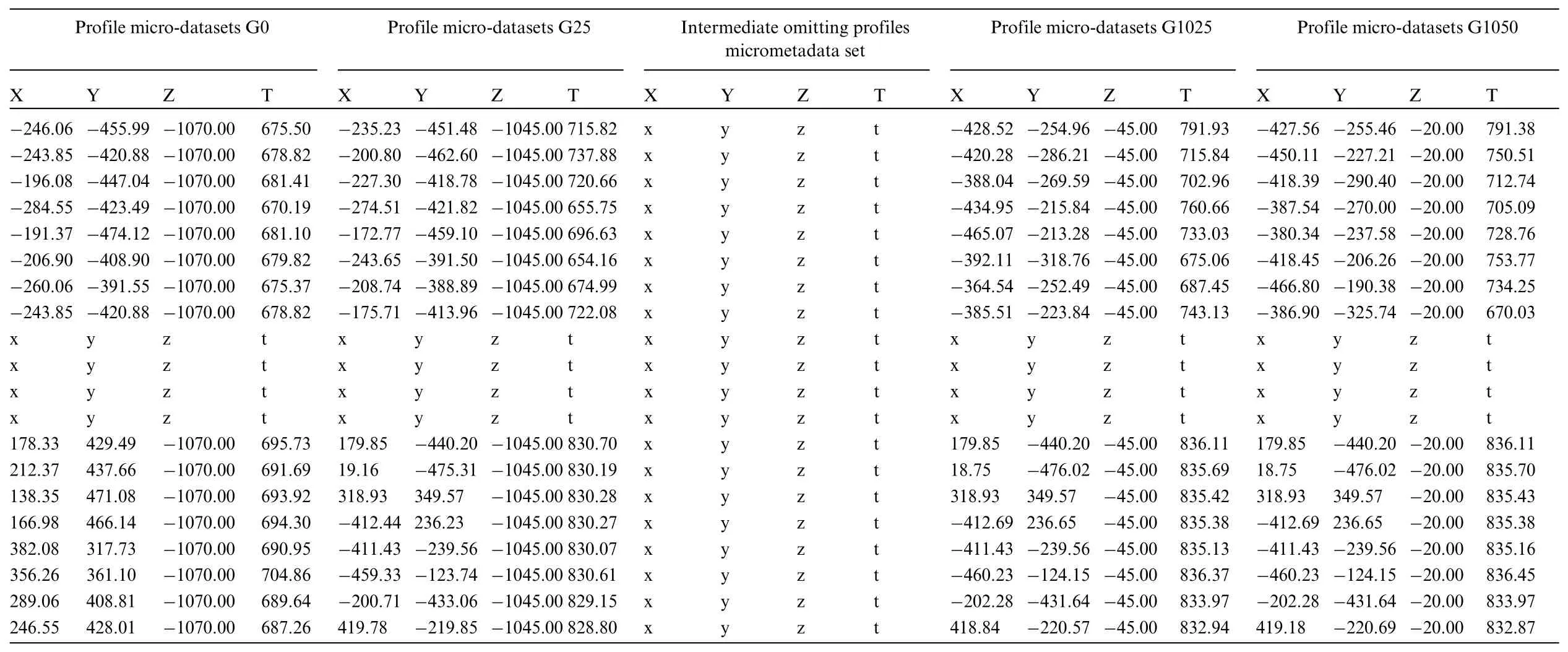
Table 12 : Data control samples obtained by conventional data extraction method

Tables 11 and 12 are the data samples extracted by the proposed data extraction method and data control samples obtained by the conventional data extraction method,respectively.The data control samples are composed of 43 profile micro-datasets,and the distance between each profile micro-datasets is fixed,which leads to inefficient data processing and data duplication;However,the data samples are composed of 35 profile micro-datasets,and the distance between each profile microdatasets varied according to the characteristics of temperature field,which results in efficient data processing and outstanding data representativeness and diversity.

In general,data points less than 1/3 of the original sample number are selected as verification data to verify the accuracy of the approximation model[36–38].In the current study,the accuracies of approximation models A1and A2are examined and compared by verification datasets.The verification datasets consist of 12 profile micro-datasets randomly selected from the sintering furnace simulation space,and each profile micro-dataset also contains 600 data points.To save space,Table 13 only shows part of the data samples.

Table 13 : Verification datasets for approximation model

The accuracy of the approximation model can be verified by three indicators:relative maximum absolute error(RMAE),root mean square error(RMSE),and coefficient of determination(R2).The mathematical expressions of the three indicators are shown in formulas(18)–(20).

In which,N is the number of verification points;yiis the true value of theith verification point;is the predicted value of theith verification point;is the average value of the verification point.RMAE is utilized to characterize the absolute maximum residual value relative to the standard deviation of the sample point output value.The closer the RMAE value is to 0,the higher the accuracy of the approximation model is.

RMSE is utilized to characterize the dispersion of samples.The closer the RMSE value is to 0,the higher the accuracy of the approximate model is.

R2is used to characterize the agreement between the predicted value and the real value.The closer the R2value is to 1,the higher the accuracy of the approximation model is.

In this study,approximation models A1and A2are constructed based on the data samples extracted by the method proposed in this study and the conventional data extraction method,respectively.The accuracies of approximation models A1and A2have been examined and compared by verification datasets,with specific results shown in Table 14.It can be seen that fewer data points are used for the construction of the approximation model A1,indicating higher computational efficiency in the approximation model A1.Meanwhile,the RMAE,RMSE and R2of the approximation model A1are better than those of the approximation model A2,indicating higher accuracy in the approximation model A1.This suggests that the simulation data samples of the sintering furnace extracted by the method proposed in this study have demonstrated higher effectiveness,and the rationality and reliability of this method have been verified.

Table 14 : Accuracy comparison of approximation models

5 Summary and Prospect

Aiming at the limitations of the multi-field co-simulation data extraction method,a multi-field cosimulation data extraction method based on adaptive infinitesimal elements is proposed in the current study.Two points are newly-introduced:First,a characteristic direction determination method based on principal component analysis with the candidate directions in the candidate characteristic direction set dimension-reduced for efficient profile direction selection;Second,an adaptive micro-step length determination method based on the fireworks algorithm in which reasonable number and position of profiles are selected by constantly adjustment on the optimization interval range according to the characteristics of the data.This proposed method has been successfully applied to the data extraction process of the multi-field co-simulation dataset of the sintering furnace.Compared with conventional data extraction methods,the proposed method has exhibited higher data extraction efficiency and accuracy.

In future studies,the adaptive simulation data extraction process for complex multi-surfaces will be focused on,with further explorations into the adaptability and influence of the extracted data samples to different approximation models and optimization algorithms.

Acknowledgement:The authors would like to thank the anonymous reviewers and the editors of the journal.Your constructive comments have improved the quality of this paper.

Funding Statement:This work is supported by the National Natural Science Foundation of China(No.52075350),the Major Science and Technology Projects of Sichuan Province (No.2022ZDZX0001)and the Special City-University Strategic Cooperation Project of Sichuan University and Zigong Municipality(No.2021CDZG-3).

Author Contributions:The authors confirm contribution to the paper as follows:study conception and design:Changfu Wan,Wenqiang Li;analysis and interpretation of results:Sitong Ling,Yingdong Liu;draft manuscript preparation: Jiahao Chen.All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials:The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.