基于平滑因子引入和神经网络优化的锂电池SOC估计方法
付炳喆,李沂洹,王 玮,李 慷
(1.华北电力大学控制与计算机工程学院,北京 102206;2.利兹大学,英国利兹LS2 9JT)
锂离子电池是实现电化学储能的重要手段,具备循环寿命长、能量密度大、自放电率低和对环境友好的优势[1]。电池荷电状态(SOC)是锂离子电池使用中的关键参数,精确获取电池SOC信息对整个系统的优化管理、安全运行等至关重要[2]。然而,由于电池内部电化学反应复杂,工作呈现较强的非线性特性,准确实时的电池SOC估计是当前电池管理的关键和难点之一[3]。
为了精确估计SOC,各国学者对多种研究方法进行了改进创新。常用的SOC估计方法可以大致分为两类:基于模型的估计方法和基于数据驱动的估计方法[4]。基于模型的估计方法以建立精确优良的模型为基础展开估计研究,其准确程度高低往往取决于模型的优劣,且受外界因素影响大,鲁棒性较弱[5]。基于数据驱动的估计方法主要使用机器学习的诸多算法来直接建立起SOC与较易测量的电压电流等参数之间的非线性关系[6],适用于所有类型的电池[7]。神经网络(NN)、支持向量机(SVM)、高斯回归过程(GPR)等算法由于其可靠性、灵活性和强大的泛化能力,越来越多地被用于锂离子电池的SOC估计中。径向基神经网络(radial basis function neural network,RBF-NN)是一种结构简单,性能优良的人工神经网络[8],但由于初始参数的随机性,直接应用于电池SOC估计时,其精度仍存在动态波动、稳定性差的难题[9]。对此,本文提出基于黄金分割-模糊C 均值-遗传(golden section method-fuzzy C means-genetic algorithm,GSM-FCM-GA)组合优化算法来实现对RBF神经网络的改进。同时,为了帮助模型学习电池电压电流快速改变时测量信号与电池内部特性相关的非线性映射,额外引入了滑动窗口内的释放电荷量作为输入信号。
为了验证所提出模型的有效性,本文基于不同温度下联邦城市行车计划(FUDS)的工况模拟环境,对比了RBF、GA-RBF、GSM-FCM-GA-RBF 的估计精度。实验结果表明,所提出的优化模型在线估计锂离子电池SOC时具有较优的性能。
1 径向基神经网络理论基础
径向基神经网络是一种结构简单的单隐层前馈神经网络,已广泛应用于函数逼近问题。径向基函数作为内置的隐含层神经元激活函数。高斯函数是常见的径向基函数,其为一种样本x到数据中心ci之间欧氏距离的单调函数,如下:
式中:σ为高斯函数的宽度。
RBF 网络中,输出结果即为对隐含层输出的线性组合。设定输入向量x为d维,采用高斯径向基函数作为激活函数的RBF 网络可表示为:
式中:q为隐含层神经元个数;y(x)为网络输出值;ci与wi分别为第i个隐含层神经元的中心与权值。
2 改进的RBF 神经网络建立
2.1 基于黄金分割优选法确定隐含层神经元个数
目前RBF 神经网络研究领域暂无统一方法确定隐含层神经元个数这一重要参数,实际应用中大部分仍采用试错法,不仅无法有效去除网络中的冗余结构,还会带来时间和人力的浪费。本文引入黄金分割优选法作为RBF 神经网络隐含层神经元个数确定的依据,具体步骤如下。
步骤1:确定选择区间,认为在RBF 神经网络中若输入层和输出层节点数分别为I和J,则隐含层神经元个数在如下区间选取。
步骤2:在区间[a,b]上确定第一个测试点g1。
其中int(·)表示对(·)进行取整运算,并记录隐含层神经元个数q取g1时模型输出结果的均方误差M1。
式中:m为样本个数;fn1和yn1分别为q=g1时第n个样本对应的实际值与模型输出值。
步骤3:确定第二个测试点g2,并记录对应的均方误差M2。
步骤4:对两次测试结果进行比较。对区间的选择标准如下:
(1)若M2>M1,截去区间[a,g2],留存区间[g2,b];
(2)若M2<M1,截去区间[g1,b],留存区间[a,g1];
(3)若M2=M1,截去区间[a,g2]、[g1,b],留存区间[g2,g1]。
步骤5:在保留的区间内不断重复以上步骤,直至得到q。
基于黄金分割法选择确定RBF 神经网络隐含层神经元个数的流程如图1 所示。
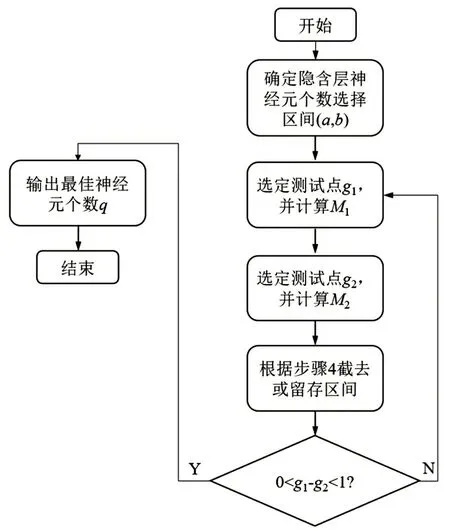
图1 黄金分割优选法流程
2.2 基于FCM 确定隐含层神经元中心
模糊C-均值(FCM)聚类算法广泛应用于聚类中心选择[10],本文以FCM 算法来根据输入样本选取RBF 神经网络隐含层神经元中心。设输入信号X=[x1,x2,...,xN]T,首先确定迭代标准ε>0 并随机生成初始聚类中心cj(j=1,2,...,p)。然后计算输入信号对中心的隶属度,公式如下:
式中:uij为输入信号xi(i=1,2,...,N)对中心cj的隶属度,并规定若存在i,k使得xi-ck=0,则uij=1;p为聚类中心个数;m为模糊系数,对m的选取方法目前仍多为经验和实验结论,一般取m=2[11]。
依据式(8)和式(9)更新中心cj:
式中:N为输入信号样本个数。计算出每次循环后的更新差值后,判断其是否小于ε。
式中:C(d)为第d次聚类得到聚类中心向量。
FCM 聚类算法的伪代码可表示如下:
算法1:基本模糊-C-均值算法
输入:输入信号维度N,迭代标准ε
初始化:最大迭代次数L,输入信号X,聚类中心C(0),模糊系数m
步骤:
1.d←0(initialization);
2.ford←0 toLdo
3.由式(7)计算输入信号对中心的隶属度
4.由式(9)更新聚类中心C(d+1)
5.Until 式(10)成立
6.end
7.Final
Return 更新后的聚类中心向量C
Update 隐含层神经元中心矢量
2.3 基于遗传算法训练RBF 神经网络
RBF 神经网络的参数选取合适与否,直接决定了估计性能的优劣。目前各国学者已经通过多种优化算法如粒子群优化算法[12]、模拟退火算法[13]等对RBF 神经网络进行训练,取得了较好的效果。
遗传算法(genetic algorithm,GA)是一种成熟的进化算法。通过对自然界生物种群繁衍进化的模拟,将适者生存的法则应用到优化求解领域[14]。其良好的寻优能力适用于RBF 神经网络参数优化问题,实现方法具体如下。
步骤1:对RBF 神经网络的隐含层神经元高斯函数的宽度及隐含层和输出层的连接权值进行编码,得到初始化种群。
步骤2:解码得到初始参数并赋予新建RBF 神经网络,利用训练样本训练后以验证样本计算输出误差。
步骤3:计算初始种群各染色体的适应度值,本文中以输出值的均方根误差为计算适应度函数值的唯一标准。
式中:fk和yk分别为第k个输出层节点的实际值与RBF 神经网络输出值;L为输出层节点个数。
步骤4:将种群中适应度高的染色体筛选出来,执行复制、交叉和变异操作,得到新一代种群。
步骤5:计算输出误差并判断是否低于阈值,若满足条件,解码得到最优的高斯函数宽度与连接权值。若不满足,返回步骤2。
根据上述步骤训练RBF 网络,经过遗传算法对网络参数进行寻优得到的RBF 神经网络模型误差较低,且泛化能力较好,在不同的应用场景中均表现出较好的鲁棒性[15]。
3 基于改进RBF网络的锂电池SOC估计
RBF 神经网络在锂离子电池SOC估计领域具有强大的应用潜力。在使用神经网络估计SOC时,通常采用锂离子电池端电压、电流和温度作为输入向量[16]。但实验表明,由于锂离子电池工作时的高度非线性动态响应特性,在充放电过程中,尤其是电池工作电压、电流大小和方向发生急剧改变时,现有的各类机器学习算法模型往往较难识别电池的外部测量信号与SOC精确的映射关系,这是由于诸如工作电压、电流和温度作为神经网络模型输入信号时,均为快速变化的实时采样的数据,是有高度时变特性的测量信息。网络只能机械地识别输入输出数据集序列的简单的对应关系,导致网络在验证集上拟合能力的丢失,泛化能力大大降低[17]。这给RBF 神经网络的学习能力带来极大挑战。
针对以上问题,经过大量实验尝试,在既有的实时测量工作电压、电流和温度的基础上,加入一个慢时变信息——滑动时间窗口内的放电容量,作为新增输入信号。该信号可以在RBF 神经网络模型学习锂离子电池输入输出数据集的非线性映射关系时,作为一个平滑因子,降低剧烈变化的电池工作信号给网络带来的不良影响。对于一个未知初始SOC信息的锂离子电池,经过若干时间的充放电,较易获得该时间窗口内的累计放电信息。采用滑动滤波技术,对某一时刻的滑动窗口时间内的释放电荷量进行累计,即可作为该时刻对应的滑动窗口的释放电荷量,可由式(12)计算:
式中:Qw为t时刻滑动窗口内的释放电量;η为库仑效率;i(t)为锂离子电池工作电流;m为该滑动窗口的长度。
本文以端电压、电流、温度和滑动时间窗口内释放电量作为输入信号,SOC作为输出信息,建立的GSM-FCM-GA优化的RBF网络有4个输入节点、1个输出节点。在保证均方误差最小的前提下,GSM选择了12 个隐含层神经元。用FCM 聚类选择合适的中心。在确定了RBF 神经网络的初步结构后,使用遗传算法对RBF 神经网络训练。初始化种群后,设定规模为100,交叉概率Pc=80%,变异概率Pm=1%。基于RBF 神经网络的电池SOC估计模型的拓扑结构如图2 所示。所提出的改进的RBF 神经网络模型估计锂离子电池SOC的总体流程如图3 所示。
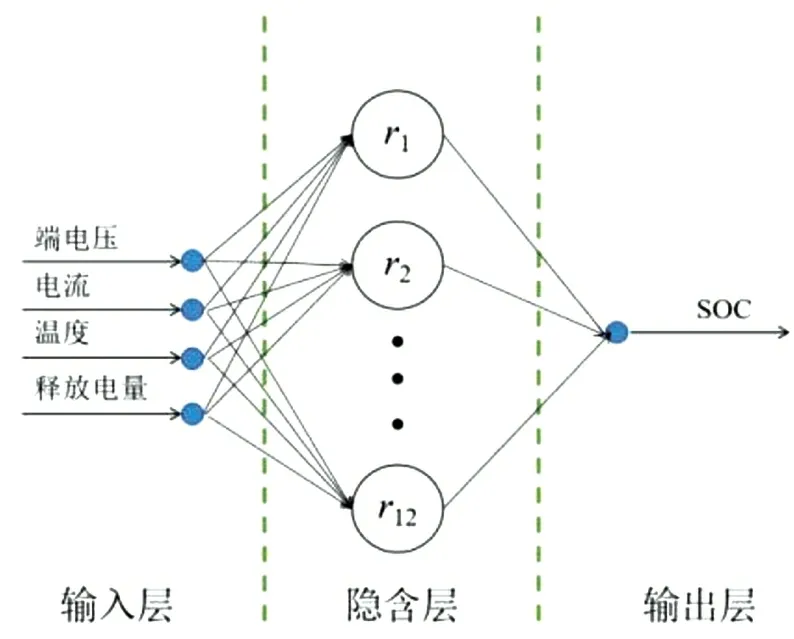
图2 用于SOC估计的RBF神经网络

图3 改进RBF网络估计SOC方法的总流程
4 实验结果及分析
为了验证GSM-FCM-GA 的优化效果,将其与原始RBF 神经网络及GA 优化的RBF 网络的估计性能进行对比。测试采用标称电压为3.2 V、标称容量为1.6 Ah 的商用圆柱形磷酸铁锂电池,最大电压3.6 V,最小电压2.0 V,初始SOC为100%。
本实验基于对FUDS 的放电工况模拟,实验平台如图4所示。将磷酸铁锂电池置于BINDER-MK电池温箱中,分别调整温度至15 和35 ℃,使用NEWARE制造的BTS4000 电池测试系统对电池FUDS 工况放电时电信号的信息采集,汇总于实验控制总机保存并处理。图5 和图6 显示了两种温度的FUDS 工况下每一次循环的电压电流曲线。

图4 实验平台结构示意图

图5 15 ℃FUDS工况电压电流变化曲线

图6 35 ℃FUDS工况电压电流变化曲线
每次FUDS 工况放电循环共历时约4 400 s,各进行8 次循环。分别采用离线训练好的GSM-FCM-GA优化的RBF 网络、原始RBF 神经网络及GA 优化的RBF 神经网络模型对电池的SOC进行估计。图7、图8分别为15、35 ℃三种模型的估计结果与真实SOC变化的对比。图中,黑色曲线代表SOC参考值,黄色曲线代表基础RBF-NN 模型估计的SOC,蓝色曲线代表基于GA 优化的RBF-NN 模型估计的SOC,而红色曲线代表本文所提出的改进RBF-NN 模型的输出。可以看出,未经任何改进的基础RBF-NN 模型的估计值相较于其他两个模型,距离SOC参考值更远;而本文所提出的模型其输出结果几乎与参考值重合。这表明,改进后的GSM-FCM-GA-RBF-NN 模型与其他两个模型相比,具有更高的估计精度。

图7 15 ℃估计结果对比

图8 35 ℃估计结果对比
由于RBF 网络模型的学习能力并非与隐含层神经元个数呈完全的正比例关系,且隐含层神经元设置过多会导致复杂度提高,收敛困难的问题。所以,为了验证所提出方法的有效性,以浮点运算数(floating point operations,FLOPs)为衡量模型复杂度的标准,在表1 中对比了不同隐含层神经元个数设置时模型性能与复杂度,训练测试数据集采用35 ℃的FUDS 工况数据。

表1 不同隐含层神经元个数设置时模型的复杂度与精度对比
从实验结果可以看出,在隐含层神经元个数超过GSM 选择的12 以后,RBF 网络模型已经可以有效地完成学习与训练任务,均方根误差(RMSE)基本维持在3.5%以内。此时继续增加神经元个数并未明显提高模型估计精度,反而大幅增加模型复杂度。由图可见,隐含层神经元个数由12 增加到22 后,RMSE 几乎没有降低,但复杂度提高了近一倍,带来结构资源的浪费,对模型收敛速度造成影响。同时,为了验证优化模型在参数寻优与模型优化问题上的卓越性能,对比了3 次GSM-FCM-RBF 模型和GSMFCM-GA-RBF 模型在FUDS 工况下的训练测试结果,记录其均方根误差与最大估计误差,见表2。

表2 使用GSM-FCM-GA-RBF 和GSM-FCM-RBF在FUDS 工况下的SOC 估计结果对比
从实验结果可以看出,多次重复训练测试实验GSM-FCM-GA-RBF 估计结果的均方根误差均保持在2%以内,最大估计误差也在3%以内。而GSMFCM-RBF 虽然经过结构的优化,但训练过程中仍采用梯度下降法等进行寻优,容易陷入局部最优的问题,导致每次训练测试的结果具有明显不确定性。最大估计误差有时可以维持在5%以内,但在训练效果不好时可以达到近10%,这给直接应用带来困难。
为了更清楚地对比三个模型的估计结果,图9 和图10 给出了三个模型在不同温度下的估计误差曲线。由图可见,改进后的模型对SOC动态工况的估计误差基本维持在2%以内,明显低于RBF 网络模型的估计误差,这得益于黄金分割优选法与FCM 聚类算法自动地确定适合于锂电池SOC估计的隐含层神经元个数与中心。改进模型迅速地逼近最优结构后,利用遗传算法的迭代全局寻优能力训练RBF 网络以得到最优参数赋予模型,完成离线训练任务。同时,图中可以看出相较于GA-RBF 模型3%以内的估计误差,GSM-FCM-GA-RBF 性能有进一步的提升,基本维持在2%以内,这体现了组合算法的优势。

图9 15 ℃FUDS工况下估计误差对比

图10 35 ℃FUDS工况下估计误差对比
上述实验结果表明,与传统的RBF 神经网络及GA 优化的RBF 网络相比,所提出的改进RBF 模型通过引入GSM 与FCM 来确定模型结构,可以去除网络中的冗余结构,降低模型的复杂度与计算量,基于电池的动态性能获得更适用于电池状态估计的径向基函数中心,提高了估计精度;进一步引入GA 来优化RBF 模型的重要参数,避免了参数初始化的不确定性对模型性能的影响,并减少了基于经验法调参带来的巨大工作量,使模型的估计性能进一步得到显著提升。
5 结论
本文提出了一种基于GSM-FCM-GA 组合优化的RBF 神经网络模型的锂离子电池SOC估计方法,通过LiFePO4电池的测试实验验证了该方法的SOC估计性能。实验结果表明,将滑动窗口内的释放电荷量作为扩展输入添加到RBF 网络的输入变量,可以增强模型的学习能力,在强动态工况下仍能给出令人满意的SOC估计结果。具体而言,所提出的GSM-FCM-GA-RBF 模型在不同温度下的FUDS 工况下的电池数据在线估计的RMSE 和最大估计误差分别维持在2%和3%以内,具有令人满意的精度。同时,在相同的训练测试数据集上,对比了原始RBF神经网络及GA 优化RBF 网络的估计性能,进一步证明了所提出方法的优越性。
由于优化模型引入GSM 确定RBF 网络隐含层神经元个数,结合FCM 确定径向基函数中心,这种组合方法克服了RBF 神经网络因参数初始化的不确定性带来估计性能不稳定的缺点,并且避免了仅使用遗传算法对参数一概寻优而陷入局部最优的可能。所提出方法旨在发挥组合方法在参数寻优问题上的优势,因此并未改变RBF 模型的本质,仍具有结构简单的特点,且并不依赖初始SOC。

