基于螺旋更新策略蜜獾优化的DV-Hop 定位算法*
鲁 兴,张来洪,任芳雨
(武汉中原电子集团有限公司,湖北 武汉 430205)
0 引言
随着物联网的发展,无线传感器网络(Wireless Sensor Networks,WSNs)得到了蓬勃发展。WSNs综合了微电子学、集成电路、无线通信等多个学科的技术,因其具有自组织性、功效低、价格低廉、灵活性强等优势,被广泛地应用于抢险救灾、环境监测、康复医疗、智慧城市建设和国防军工等领域[1-4]。WSNs 定位技术主要有基于测距的算法和非测距的算法2 种。基于测距的定位算法精度较高,但对硬件要求也高,在大规模的网络环境中实现较为困难。非测距的定位算法不需要额外的硬件,实现简单、成本较低,广泛应用于大规模无线传感器网络中。
距离向量跳段(Distance Vector Hop,DV-Hop)算法因其实现简单、通信开销小等特点成为受到关注最多的非测距算法。传统的DV-Hop 算法由于跳距处理误差和最小二乘的累积误差等原因导致定位精度较低。为了解决传统DV-Hop 算法定位精度低的问题,国内外学者提出了大量的改进策略[5-7]。邴晓瑛等人[8]提出采用多通信修正跳数,并采用加权的思想修正未知节点的平均跳距,但未知节点的位置估计过程仍采用最小二乘法,没有消除最小二乘法求解本身带来的误差。文献[9]和文献[10]将粒子群优化算法或人工蜂群优化算法引入到传统DV-Hop 算法中,发现新算法可以减小最小二乘导致的误差,一定程度上提高了定位精度,但该过程未改进粒子群算法以适应WSNs 场景,定位精度有待进一步提升。文献[11]采用基于自适应策略的灰狼优化算法来替代传统DV-Hop 的最小二乘法,新算法的收敛速度快、定位精度高,但忽略了未知节点平均跳距的误差,定位精度有待进一步提升。文献[12]提出了基于差分进化的节点定位方法,但差分进化受参数影响较大,控制参数选取不合适,种群进化中容易失去多样性,无法找到最优解。
为此,本文分析传统DV-Hop 定位算法的不足,提出了一种结合未知节点平均跳距修正和改进型蜜獾算法(Honey Badger Algorithm,HBA)的DVHop 定位方法,以期弥补传统DV-Hop 定位算法的不足,提高定位精度和稳健性。
1 DV-Hop 算法及误差分析
DV-Hop 算法主要分为3 个阶段,具体如下文所述。
(1)未知节点与锚节点间最小跳数的估计。节点之间相互交换Hello 包,Hello 包中包含了跳数及锚节点坐标,网内未知节点获得锚节点坐标及离各锚节点的最小跳数。
(2)计算未知节点与各锚节点间的距离。锚节点之间相互传递Hello 包后,获知各自的位置信息以及互相之间的最小跳数。锚节点可利用式(1)计算平均跳距。
式中:(xi,yi),(xj,yj)分别为锚节点i和锚节点j的位置坐标,num_hop为锚节点i和锚节点j的最小跳数。锚节点将自己计算得到的平均跳距向外广播。未知节点将第1 个收到的锚节点的平均跳距作为自己的跳距,则根据式(2)可以估算出未知节点u与锚节点i之间的距离dui。
式中:num_hopui为未知节点u与锚节点i间的最小跳数,Hopsizeu为未知节点u选取的平均跳距。
(3)计算未知节点位置坐标。获取锚节点的位置坐标以及未知节点到锚节点的距离,利用最小二乘法可求得未知节点坐标。
式中:X为未知节点位置,A和b为与锚节点位置以及未知节点与锚节点间距离相关的已知向量。通过上述过程,传统DV-Hop 算法完成了未知节点的定位。由以上定位过程分析可知:在传统DV-Hop算法中,未知节点以收到的最近的锚节点的平均跳距值作为自己的平均跳距值,没有全面考虑网络中的锚节点信息,在多跳网络中,该取值方法不能真实反映网络中的跳距情况,未知节点平均跳距产生的误差会导致节点间距离与实际距离相差过大,因此需要综合考虑多个锚节点的平均跳距离来准确地估计未知节点在网络中的平均跳距[13,14]。此外,跳距误差会在最小二乘法求解未知节点位置阶段被进一步扩大,最小二乘法本身也会有较小的解算误差,会造成误差累积[15]。
2 DV-Hop 算法的优化
2.1 未知节点的平均跳距修正
传统的DV-Hop 定位算法中,未知节点将离它最近的锚节点所估计的平均跳距值作为其平均跳距值,但单个锚节点的平均跳距值无法反映整个网络的实际情况。
由文献[16]可知:传统DV-Hop 算法计算出的锚节点平均跳距比实际值偏小,并且锚节点数量越多,偏小误差累加越大。为了使未知节点估计的平均跳距值更加准确,基于上述偏小误差分析,将未知节点收到的多个锚节点所估计的平均跳距值、锚节点比例进行综合考虑,修正后的未知节点在网络中的平均跳距如下:
若0 ≤Bratio<0.5,则
若0.5 ≤Bratio<1,则
式中:UhopSize为未知节点在网络内的平均跳距;BhopSizeave为锚节点平均跳距均值,即对未知节点所收到的所有锚节点的平均跳距取平均值;BhopSizemax为未知节点所收到的所有锚节点的平均跳距的最大值;Bratio为锚节点占总节点的比例。BhopSizemax和BhopSizeave的计算过程如下:
式中:Nb为未知节点所收到的锚节点个数。当锚节点较多时,用锚节点平均跳距最大值BhopSizemax来减小偏小的误差。当锚节点较小时,结合锚节点平均跳距均值BhopSizeave和锚节点平均跳距最大值BhopSizemax进行综合处理,修正后的未知节点平均跳距能够更好地反映网络的实际情况。
2.2 改进的蜜獾优化算法
HBA 作为一种新兴的元启发式优化算法,主要模拟蜜獾挖掘和寻找蜂蜜的智能觅食行为,因其与多种著名的元启发式算法如模拟退火(Simulated Annealing,SA)、鲸鱼优化(Whale Optimization Algorithm,WOA)等相比,在搜索复杂空间的优化问题上更为有效、结构简单,故可广泛地应用于许多场景。为了减小最小二乘算法估计未知节点坐标带来的累积误差,引入改进的HBA 算法来提高节点的定位精度。相较于传统的HBA 算法,改进的HBA 算法首先引入了Sobol 序列来提高初始种群的遍历性,其次使用螺旋更新机制来加强HBA 算法的局部搜索能力,最后采取镜像策略规避估算位置越界的情况。
改进的HBA 算法的步骤大致分为确定适应度函数、种群初始化、定义气味强度、更新密度因子、更新个体位置和越界处理。
2.2.1 确定适应度函数
改进的HBA 算法中,首先确定适应度函数以评估搜索位置的优劣,依据适应度函数向正确的方向进行搜索。适应度值的计算式为:
式中:n为该未知节点能接收到n个锚节点的信号,(x,y)和(xi,yi)分别为未知节点和锚节点i的坐标,disi为对未知节点平均跳距修正后计算得到的锚节点i与未知节点之间的距离。
2.2.2 基于Sobol 序列的种群初始化
在运用群智能算法时,首要需对种群中的个体分布进行初始化。若初始种群分布不佳,无法充分涵盖取值空间,算法最终可能会收敛到质量不佳的解上,此时则需要增加迭代次数或种群个体数量来使解达到最优值,这会提高算法的计算量。传统的蜜獾优化算法采用随机分布的种群初始化方法,无法保证初始个体在搜索空间中合理分布。为了避免初始化种群随机分布产生的问题,文中利用Sobol序列来初始化种群。
Sobol 序列是一种低差异序列,在种群的各个维度上均以2 为底数的radical inversion 组成,将尽可能均匀的初始点放置至多维立方体中,具有遍历性、规律性的特点,可以用来初始化蜜獾种群,确保种群分布更为均匀和广泛。
设全局解的取值范围为[lb,ub],由Sobol 序列产生的第i个随机数为Ki,则种群的初始位置P0i可以表示为:
假设种群规模为100,分别采用随机法和Sobol序列初始化种群,种群分布如图1 和图2。由图1和图2 可看出,Sobol 序列产生的初始种群分布更加均匀,扩大了蜜獾群的搜索范围,增加了群体的多样性,有利于算法跳出局部极值,一定程度上提高了算法的计算效率。

图1 随机初始化种群
图2 Sobol 序列初始化种群
2.2.3 定义气味强度
蜜獾依据气味寻找猎物,因此猎物气味越强越大,则表明离猎物越近,被搜索到的速度越快。气味强度的定义如下:
式中:Ii为第i只蜜獾感受到猎物的气味强度;S为猎物的集中强度,S=(Pi-Pi+1)2;ηi为猎物Pprey与第i只蜜獾Pi的距离,ηi=Pprey-Pi;r2为(0,1)的随机数。
2.2.4 更新密度因子
密度因子α随着迭代次数的增加而减少,确保算法在勘探和开发之间的平稳过渡。
式中:C0为大于1 的常数,取值不同会影响试验结果,取2;lmax为最大迭代次数,l为当前迭代次数。
2.2.5 更新个体位置
传统HBA 算法的位置更新分为挖掘阶段和采蜜阶段,该算法使用改变搜索方向的标志F,避免陷入个体位置的局部最优解。然而传统蜜獾算法的挖掘阶段沿着类心形轨迹运动,这会导致算法局部寻优能力较弱。挖掘阶段的运动轨迹对算法最终的寻优位置具有重要的影响。若寻优轨迹不适合,算法很容易陷入局部优化,收敛速度减慢。
由前人研究可知:WOA、飞蛾火焰算法采用螺旋飞行路径均具有较好的局部寻优能力。受此启发,本文提出一种基于螺旋更新策略的局部寻优方法。在传统蜜獾寻优算法的基础上,增加螺旋更新阶段,增强蜜獾算法的局部搜索能力。
(1)挖掘阶段。蜜獾寻找猎物过程类似于心形,心形运动的轨迹可表示为:
式中:Pprey为当前发现的猎物的全局最佳位置;β为猎物获取食物的能力;ηi为猎物和第i只蜜獾的距离;r3,r4,r5均为(0,1)的随机数;F为改变搜索方向的标志,由下式确定:
式中:r6为0 至1 之间的随机数。
(2)采蜜阶段。蜜獾随着导蜜鸟找到蜂巢,计算过程如下:
式中:r7为0 至1 之间的随机数。
(3)螺旋更新阶段。设置1 个随机参数r8,由r8来决定蜜獾寻优的更新公式,当r8<0.3 时,则依据个体当前位置更新,否则依据种群最优位置进行更新,计算过程如下:
式中:ηj为第j只蜜獾个体与目标猎物的距离;b为对数螺旋形状参数;t取值为[-1,1];Pnew为蜜獾寻优更新后的位置;Pi为蜜獾个体当前所处位置;l为迭代的次数;Pb为当前所估计的猎物位置,即全局最优位置。
螺旋更新的轨迹如图3 所示。其中,Mi为第i只蜜獾个体,Ni为目标位置,个体位置围绕目标位置Ni进行螺旋更新。通过修改参数t,个体位置可以收敛到目标位置的任意领域范围内。螺旋方程表明个体可以环绕在目标位置的周围而不仅是在它们之间的空间搜索,保证了算法的全局开发和局部搜索能力。
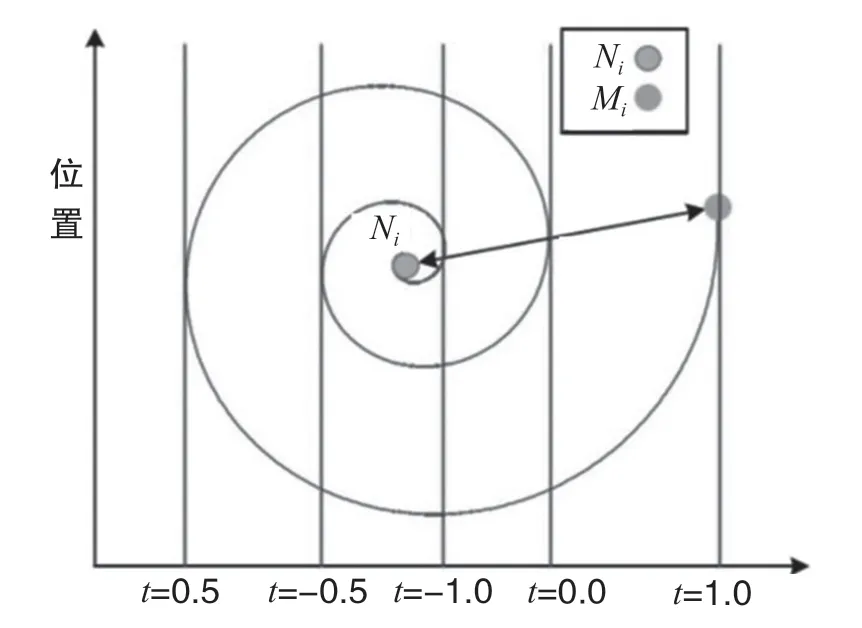
图3 对数螺旋轨迹
2.2.6 越界处理
通过改进的HBA 算法估计出未知节点的最优位置,但有时估计出的未知节点会超出规定的网络区域,发生越界情况。在现实应用中,所有节点部署在规定区域内,越界的节点将无意义。
本文提出了镜像策略来处理节点越界情况。在节点越界的维度,对其进行镜像处理,将其映射回合法区域内。具体映射变换过程如下:
若未知节点求解出的坐标为(xi,yi),其在x上的取值范围为[xlow,xup],在y上的取值范围为[ylow,yup]。由式(16)、式(17)求出的解即可不出现越界情况,保证了解的现实意义。
综上,文中所提基于螺旋更新策略蜜獾优化的DV-Hop 定位算法的流程如图4 所示。

图4 改进型DV-Hop 算法流程
(1)设置相关参数,如蜜獾个体的数目、蜜獾种群维度、蜜獾捕食能力β、密度因子中的常数C0、最大迭代次数lmax、搜索空间的上下界ub和lb、对数螺旋形状参数等。
(2)修正未知节点的平均跳距,并求解出未知节点与锚节点间的距离。依据锚节点个数比例、所有锚节点平均跳距的最大值和所有锚节点平均跳距的平均值3 个因子来修正未知节点平均跳距。将此修正的平均跳距乘以未知节点到各锚节点的最小跳数,从而得出未知节点与各锚节点间的距离。
(3)采用Sobol 序列初始化蜜獾种群。
(4)进入迭代循环后计算个体位置更新公式所需要的一些参数,如密度因子α、气味强度I、搜索方向F等,用蜜獾挖掘阶段和采蜜阶段的式(12)和式(14)更新个体位置。
(5)为了进一步提高解的精度,采用式(15)进行螺旋更新,并计算种群个体适应度值,更新个体最优值和全局最优值。
(6)判断是否达到迭代次数上限,没有则返回步骤(4),达到迭代上限,则输出最优个体位置。
(7)判断所有估计的未知节点位置是否越界,若越界按式(16)和式(17)进行越界处理,否则不处理。
3 仿真实验及结果分析
为了验证文中所提算法的定位性能,对比分析所提算法与传统DV-Hop算法、基于跳距修正的DVHop 算法和基于POS 的DV-Hop 算法。在100 m×100 m 的网络范围内随机部署未知节点和锚节点。文中算法的蜜獾优化种群规模设为100,最大迭代次数设为50,并采用归一化的平均定位误差来定量地评估各算法的定位精度,其定义如下:
式中:Nu为未知节点个数,R为节点的通信半径,为估计的未知节点位置,(xi,yi)为未知节点的真实位置,σ取连续仿真30 次的平均值结果。
3.1 总节点数对定位性能的影响
首先,分析总节点数对定位性能的影响,其中总节点数从60~260 变化,锚节点占总节点数的比例为25%,通信半径为30 m,平均定位误差随总节点数的变化趋势如图5 所示。由图5 可知:当总节点数为60 时,DV-Hop 算法的平均定位误差为0.351,跳距修正的DV-Hop 算法的平均定位误差为0.310,基于POS 的DV-Hop 算法的平均定位误差为0.255,而本文提出的算法平均定位误差为0.205。随着节点总数的增加,平均定位误差随之降低。究其原因可能在于,在一定区域内,随着节点总数的增加,节点之间连通性变强,节点收集到更多的信息,从而使定位误差下降。当然,当总节点数达到一定的值时,平均定位误差下降的速度明显减缓。相比于 DV-Hop 算法、跳距修正的DV-Hop 算法和基于PSO 的DV-Hop 算法,本文所提算法平均定位误差最低,这归功于本文所提算法修正了未知节点平均跳距以及采用改进的HBA 算法来估算未知节点位置。
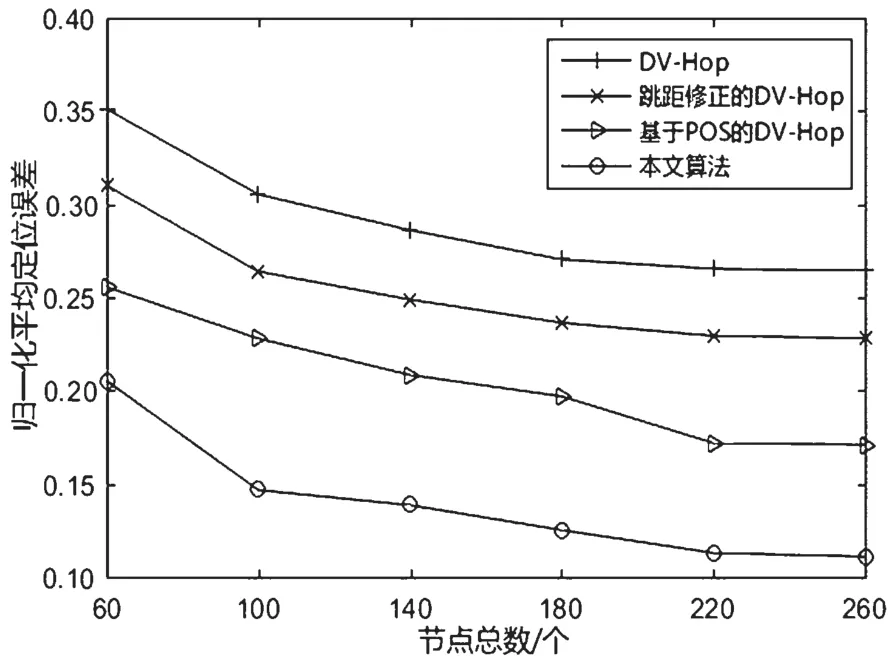
图5 总节点数对定位精度的影响
3.2 锚节点所占比例对定位性能的影响
将节点总数设置为100,通信半径设置为30 m,锚节点所占比例为20%~70%,仿真结果如图6所示。在锚节点较少时,所有算法的平均定位误差均较大。随着锚节点比例的增加,各算法的平均定位误差均减小。这是由于较多的信标节点可以使跳距估计更为准确。当信标比例大于45%时,各算法平均定位误差下降的趋势明显减缓。从4 种算法的对比可以看出,最终本文所提算法的误差小于DVHop 算法、跳距修正的DV-Hop 算法、基于POS 的DV-Hop 算法的误差,且分别平均降低56.17%、44.70%和28.12%。
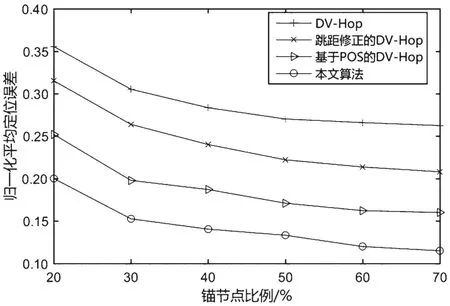
图6 锚节点比例对定位精度的影响
3.3 通信半径对定位性能的影响
在节点总数为100,信标所占比例为25%时,通信半径在20~45 m 之间变化,观察通信半径对定位性能的影响。各算法的平均定位误差随通信半径R的变化曲线如图7 所示。随着通信半径的增加,平均定位误差不断下降。在通信半径为20~40 m 之间时,通信半径的增加会极大提升网络连通性,快速提高定位精度。当通信半径大于40 m 时,平均定位误差下降的速度减缓,不再有效提高定位精度。对比分析可知:最终本文所提算法的定位误差与DV-Hop 算法、跳距修正的DV-Hop 算法、基于POS 的DV-Hop 算法相比分别降低了54.95%、45.51%和25.19%。
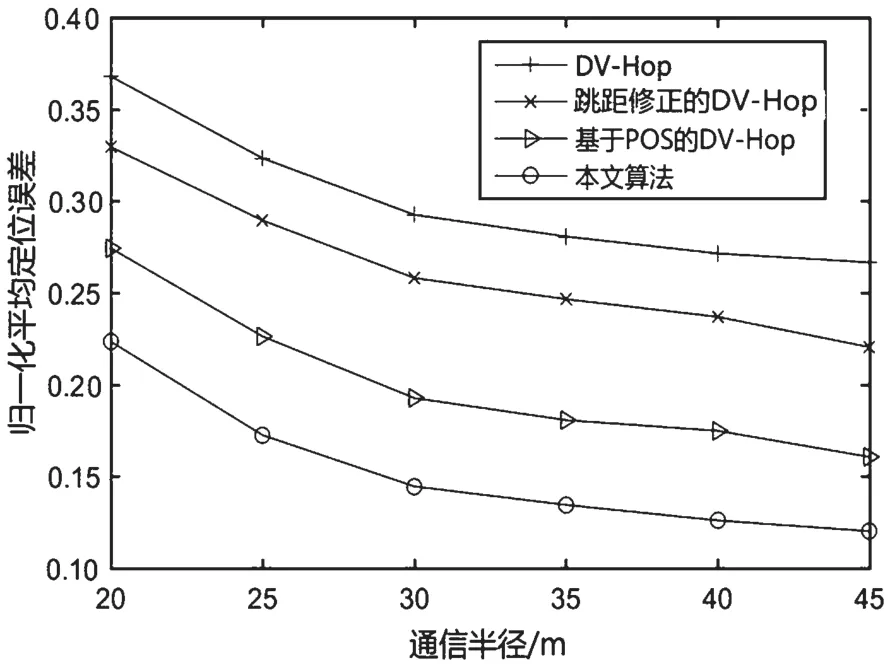
图7 通信半径对定位精度的影响
4 结语
针对传统DV-Hop 算法定位精度不足的问题,本文首先分析了其产生误差的原因,提出了一种改进的HBA 算法与基于未知节点平均跳距修正的DV-Hop 算法相结合的融合算法。该融合算法首先采用依据信标节点比例对未知节点平均跳距进行分段修正以缩小跳距估计误差,再针对传统蜜獾算法的不足进行了改进。结果表明:在不增加任何通信开销时,文中所提算法能有效提高定位精度和稳定性。但文中所提算法的计算量较传统的DV-Hop 算法有所提高,后续研究在提高计算精度的同时能兼顾计算复杂性。

