基于非对称离散高斯似然的深度图像压缩方法*

罗 春，何小海，卿粼波，任 超，熊淑华

（四川大学 电子信息学院，四川 成都 610065）

0 引言

近些年来，深度学习技术在图像压缩领域大放光彩。不同于传统图像压缩算法，深度学习方法学习一个端到端的压缩框架，涉及变换、量化和熵编码过程。相较于传统压缩编码技术，如JPEG 和BPG，深度学习方法具有更优的率失真性能和视觉感受。

随着深度学习技术在图像压缩领域的应用，许多先进的压缩算法被提出。Ballé 等人[1]先提出了端到端的图像压缩算法用于压缩自然图像，后续又提出了超先验模型[2]，对隐变量用高斯分布建模。Minnen 等人[3]引入了自回归先验预测分布参数，但使得模型只能串行运行，限制了模型的计算速度。Cheng 等人[4]在此基础上采用了混合高斯分布模型对隐变量进行更细粒度的建模，搭配非局部注意力机制和自回归模型用于熵编码。由于率失真和卷积的限制，纯卷积网络无法真正去除隐变量间的相关性，导致率失真性能的瓶颈。为此，研究者们将transformer 引入图像压缩领域，突破率失真性能的瓶颈，实现高效的图像压缩编码技术。Zou 等人[5]提出了即插即用的窗口注意力构建编解码器，结合局部和全局相关性的同时依旧保持较高的计算效率，使得压缩的图像满足预期。Liu 等人[6]结合transformer 的非局部特性和卷积网络的局部特性，构造编码器和熵模型，相比于纯卷积神经网络或纯transformer 具有更大的感受野，在Kodak 数据集上达到了最优水平。

许多工作致力于研究如何高效地将图像映射至隐空间，由于卷积和transformer 天然存在的局部和全局相关性，隐变量间普遍地存在统计依赖。因此，在隐空间中如何选取隐变量分布是一个需要解决的问题。此前的工作是选取高斯分布建模隐变量，在给定均值和方差的情况下高斯分布具有最大的熵，这对建模未知分布是有益的，但是也伴随熵增加带来的额外码流。

针对上述问题，本文提出一种结合语义信息的图像压缩算法。该算法引入Spike and Slab[7]先验，并结合语义信息建模隐变量，可以有效地降低图像码率，同时保持高质量的解码图像。

1 深度图像压缩技术

深度图像压缩的经典流程为先经过编码器E得到隐变量的表示y，随后经过量化操作Q得到离散化的隐变量表示，最后经过解码器D得到解码后的图像，整个过程可以表示为：

式中：φ和θ分别为编码器和解码器的参数。在此基础上，引入超先验信息建模隐变量，其过程可以表示为：

式中：φh和θh分别为超先验编码器Eh和超先验解码器Dh的参数。超先验模型具体的原理如图1（a）所示。图1（b）展示了一种改进后的深度图像压缩编码框架——上下文超先验模型，其使用自回归模型，可以有效地学习到隐变量参数，缺陷是限制了模型的并行化部署。

图1 模型原理

后续的深度图像压缩技术大多沿用了超先验的框架，主要研究编解码网络框架和熵模型的构建。比如，文献[8]、文献[9]和文献[10]使用残差网络高效地压缩隐变量，从而获得更高质量的解码图像。文献[11]引入注意力机制来重构编解码器，例如，使用空间注意力机制学习特征通道间的交互，有效地提取空间依赖，以及利用自注意力克服卷积的归纳偏置的缺陷，建立全局的相关依赖。熵模型是一种收发双方共享的模型，也是影响深度图像压缩性能的重要环节。文献[12]使用通道自回归模型，相较于空间自回归模型有优势。文献[13]和文献[14]结合空间通道自回归模型，在不影响运行速度的前提下实现了性能的提升。

随着研究的推进，编解码器和熵模型的效果已逐渐达到瓶颈，依靠增加计算量实现性能提升的方法逐渐变得低效。因此，如图1（c）所示，从隐变量分布出发，引入非对称高斯分布，即Spike and Slab 分布，以实现隐变量分布的熵减过程。

2 非对称深度图像压缩方法

2.1 问题方程

提出的非对称深度图像压缩结构如图2 所示。如其他压缩模型一样，输入图像经过编码器后得到隐空间表示，但并不马上进行量化，而是经过一个“熵减”过程，具体地，可以分为语义信息提取和稀疏化过程。语义信息提取学习二进制掩码s，经过稀疏化后的隐变量具有高度语义相关的稀疏性，将限制学习的高斯分布参数，趋向熵减少的方向。具体地，经过熵减阶段后的隐变量分布可以表示为：

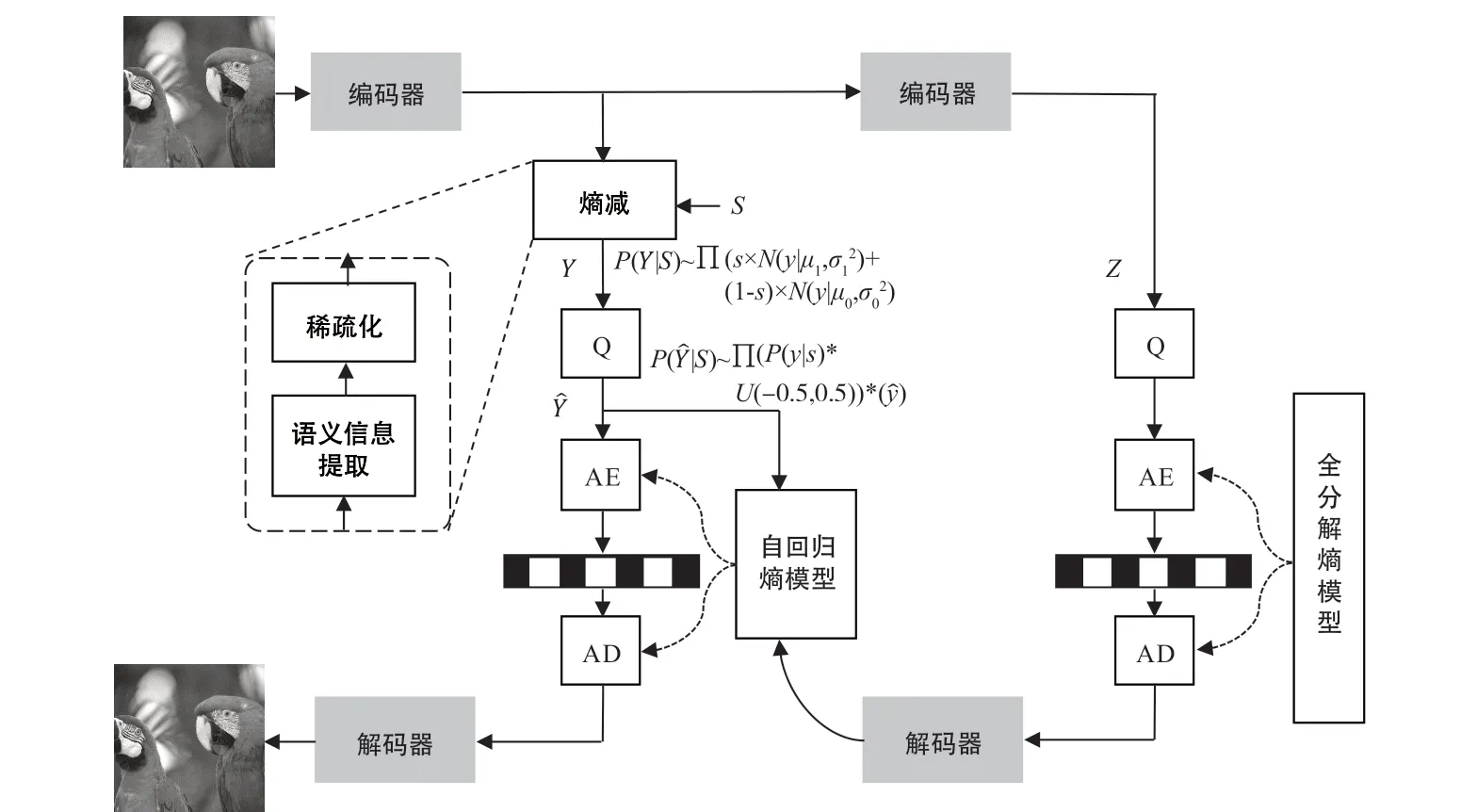
图2 非对称离散高斯似然的深度图像压缩方法网络结构

式中：σ1＞＞σ0。对于那些语义冗余的隐变量（s=0），学习的高斯分布趋向于一个冲激函数，离散化后的隐变量具有较小的熵。

为了训练端到端的图像压缩框架，使用下列的损失函数更新网络参数：

式中：λ为一个超参数，用于比特率和失真率间的权衡；d(,x)为衡量重建图像和原始图像差异的函数，通常使用均方差（Mean Square Error）函数；R()和R()为传输离散隐变量和超先验所需要的码率。

2.2 语义信息提取

借助图像语义信息，可以获得文本相关的稀疏结构，有助于去除变量间的相关性。具体地，如图3 所示构造了卷积—通道注意力级联的掩码提取器G_mask，对输入图像的各个通道进行不同的非线性映射，自适应地调整各个通道间的注意力权重，强化重要特征，削弱无关特征，最终得到联系紧密的特征图。经过掩码头Mask_head 和阈值Threshold模块的二值化处理，将得到语义掩码S∈{0,1}N。具体的流程可表示为：

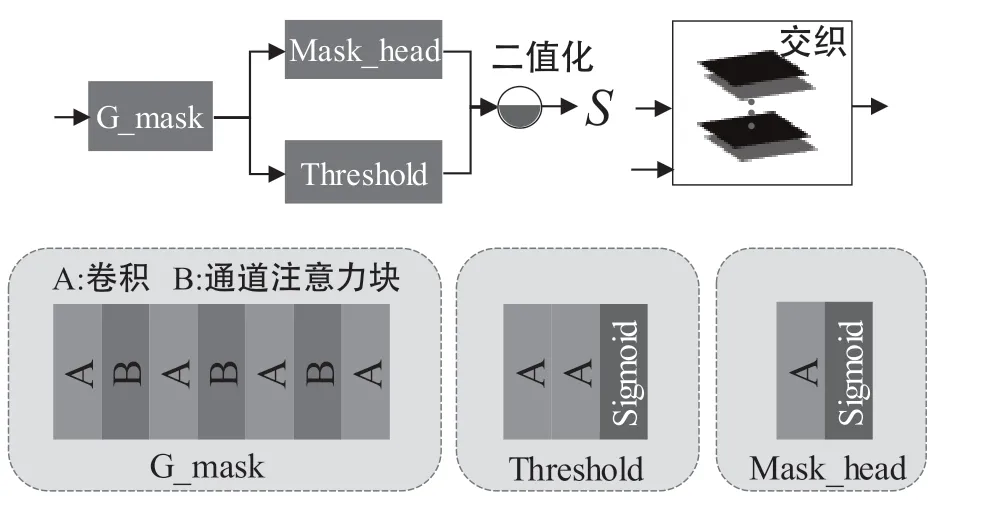
图3 语义信息提取过程

获得语义掩码后，和隐变量进行交织操作，拉近隐变量和对应掩码的空间距离。具体地，将对应通道平面堆叠形成新的张量ym，用于后续的稀疏化处理。

2.3 含参稀疏化过程

结合卷积的局部特性与transformer 的全局特性[15]，本文使用卷积构造含参稀疏化过程，如图4所示。具体地，将输入的张量ym经过卷积网络Q，K和V映射到特征空间得到Q,K,V∈ℝB×C×H×W，经过矩阵转换操作后变成适合操作的矢量形式Q,K,V∈ℝB×L×C，最终得到捕获相关性的注意力特征为：

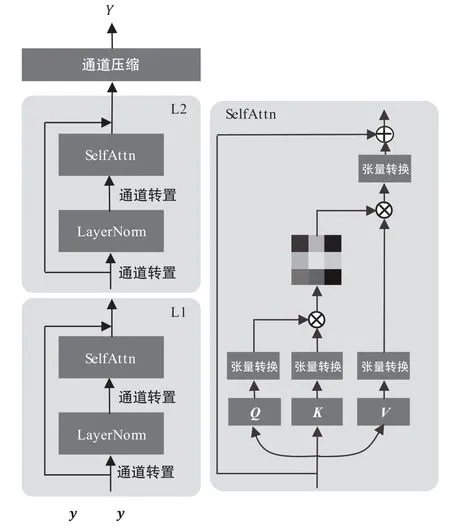
图4 含参稀疏化过程

式中：γ和dk分别为缩放因子和矢量的维度。稀疏过程可以降低计算的复杂度，提高计算效率。相较于无参稀疏化过程，含参稀疏化过程可以自适应地调节稀疏程度，面对复杂环境具有较强的适应性，适合端到端的学习方式的部署。

3 实验分析

3.1 实验设置

模型训练中使用Vimeo90K 数据集作为训练集，它包含153 939 张裁剪空间尺寸为256×256 的图像，通用数据集Kodak 作为测试集。在训练的初期，使用Adam 优化器对压缩网络的参数进行优化，batchsize 设置为24。初期的学习率设置为0.000 1，在训练的后期将学习率设置为0.000 01。

模型使用式（4）优化率失真曲线。具体地，使用均方差（Mean Square Error，MSE）作为失真项，超参数λ选择为{0.001 8,0.003 5,0.013}，并采用pytorch 框架，在GTX2080Ti 上进行训练。

3.2 实验结果分析

本文比较了当前的先进的图像压缩算法，包括Cheng[4]、BPG、hyperprior[2]和多功能视频编码（Versatile Video Coding，VVC），从客观指标（率失真曲线）和主观感受两个方面评价参与比较的压缩算法的优劣。

图5 展示了不同压缩算法在通用数据集Kodak上的率失真性能。从图中可以看出，当bpp 位于0.2～0.3 的区间时，本文所提方法和VVC、Cheng 具有相似的性能，但在bpp 小于0.2 大于0.3 的区间内时，本文所提算法相较于VVC 和Cheng 具有明显优势。

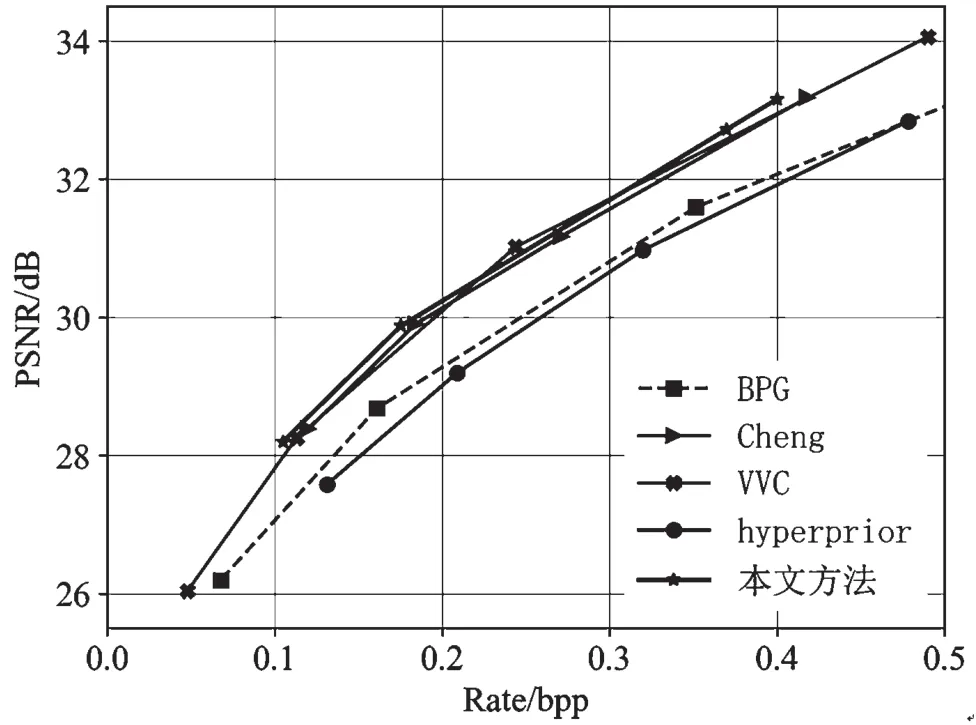
图5 不同压缩算法在Kodak 数据集上的率失真曲线

图6 展示了不同压缩方法在Kodak 数据集图像kodim23 上的解码图像。相较于其他方法，本文提出的方法在保持纹理细节方面具有优势。

图6 图像kodim23 的可视化解码结果（bpp/PSNR/SSIM）

3.3 隐变量分析

图7 展示了隐变量的可视化结果。可以看出，随着隐变量的通道层数的增加，通道特征逐渐变得稀疏，意味着分配的码流越来越少。在纹理细腻的区域，如帽子、围巾区域，一直都在分配码流；而脸部等高频成分较少的区域，只在前几个通道分配码流。这些实验结果验证了本文提出的方法可以有选择地改善码流分配。

图7 掩码后的隐变量

4 结语

本文主要研究了深度图像压缩技术中的率失真优化问题，主要思想是在隐空间借助通道注意力提取语义信息，并基于自注意力机制构建含参稀疏化过程，实现单高斯分布向非对称高斯分布的迁移，以节约码流。实验结果表明，本文提出的方法在节省码率、优化率失真性能上具有良好表现。