基于智能算法优化的嵌入式机器人运动控制方法

高兆申

泰山科技学院 山东 泰安 271000

引言

差分驱动的机器人具有结构简单、运动能量消耗少的特点，在很多场合获得了广泛的应用。例如，在抗震救灾中，可以利用这种机器人投送救援物资[1]；在野外探测中，可以利用这种机器人搭载多功能相机获得所需要的图像[2]。但是，在机器人的运动控制中，由于欠驱动性质的存在，导致控制律设计困难。本文利用嵌入式系统的自主控制和即时通讯优势，设计了一种基于智能算法优化的运动控制律，从而使机器人按照预定的轨迹运动。这种控制方法增加了机器人执行多种任务的能力，有利于推动这种机器人获得更广泛的应用。

1 机器人运动模型

机器人采用“双轮差分驱动+单轮自由支撑”的结构实现平面内的运动。两个后采用同一连杆连接，利用差分驱动的方式为机器人的运动提供动力。其中，前进的动力由两个车轮的一致运动提供，转向的动力由两个车轮的差速运动提供。前轮发挥对车体的支撑作用，并不提供动力[3]。机器人的机械结构如图1所示。

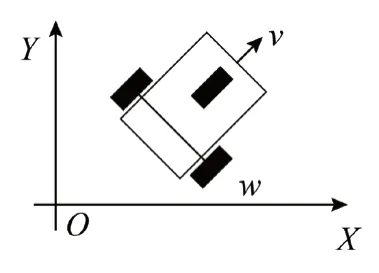
图1 差分运动机器人机械结构

在图1所示的坐标系XOY中，机器人以前向速度v、角速度w运动。其中，v来自于两个后轮的协同运动，w来自于两个后轮的差分运动。定义机器人的运动轨迹为（x，y，θ），其中（x，y）表示其在平面内的坐标位置，θ表示转向角。运动轨迹与运动速度之间的关系，可以表示为[4]：

在公式（1）中，机器人的运动模型显然是一个欠驱动系统。也就是说，通过对速度变量v和w施加控制力，很难完全控制住x，y和θ三个状态变量。这个运动控制律的设计带来了难度。很多文献指出，对欠驱动系统实施运动控制，可以选择其中的部分状态变量作为被控制量、选择剩余的状态变量为被跟随量，通过与控制变量之间联立等价的对应关系，从而完成控制律的综合设计。

2 机器人物理实现

在图1所示的机械结构基础上，增加智能载荷构建完整的机器人系统。机器人的两个后轮由电机分系统提供驱动控制信号。电机分系统由转子、定子、霍尔元件以及信号磁环等组成。其中，转子在定子内部通过电磁感应运动，从而产生稳定的直流电。霍尔元件和信号磁环完成直流电的换相，实现输出功率的稳定调节。同时，利用信号磁环可以将电流的相位信号与机器人的位置信号实现关联。在电机分系统的基础上，设置位置监测传感器，通过实时观测机器人的运动状态调整电机分系统的输出功率，从而完成机器人的运动控制。此外，设计PLC控制器，用于对机器人的运动信号进行控制[5]。

完整的机器人系统，拓扑结构如图2所示。

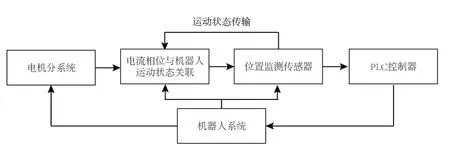
图2 机器人系统拓扑结构

在图2所示的机器人系统拓扑结构中，PLC控制器采用嵌入式方案设计。在PLC内部，设计ARM模块，将运动控制律烧录其中；利用机械传动装置将ARM模块的输出信号转换为控制机器人后轮的力矩信号，驱动机器人进行差分运动。同时，分别利用位置和速度传感器对机器人的实时运动状态进行采集，将运动状态信息与参考轨迹信息进行实时对比。此外，PLC控制器中集成了通讯模块，用于与外界实时传输信号，便于对机器人的运动状态进行监测。PLC控制器的内部结构如图3所示。

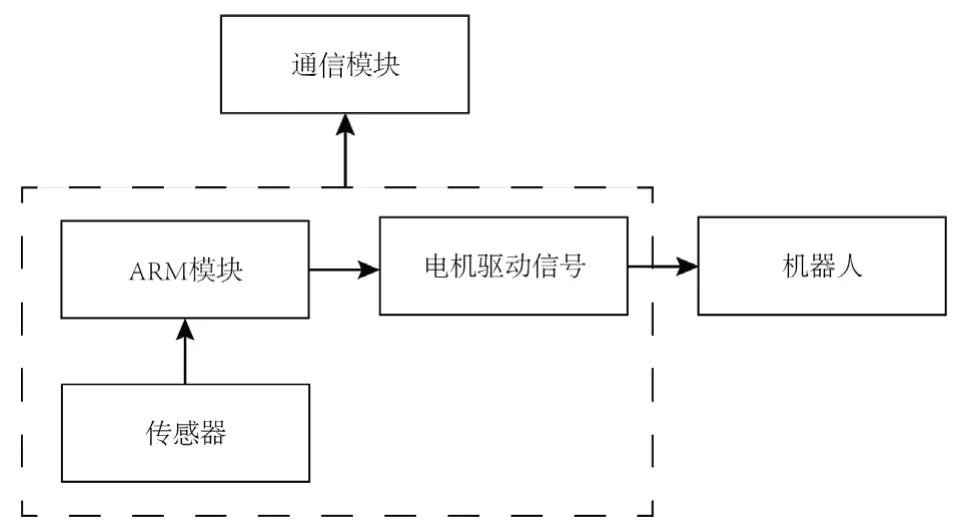
图3 PLC控制器内部结构

3 机器人运动控制律设计

机器人的运动控制律被烧录在PLC控制器内部，通过产生驱动信号控制速度变量v和w，进而驱动运动轨迹（x，y，θ）按照预期变化。在实际场景中，假设机器人预期的运动轨迹，也被称为参考轨迹，如下所示：

式中，vr和wr分别表示参考前向速度和角速度，(xr，yr，θr）表示参考轨迹，也就是期望的机器人的运动状态。

将公式（1）减去公式（2），并将计算结果转变成PLC控制器可以测量的量，结果如下：

式中，（xe，ye，θe）表示运动轨迹的跟踪误差。

为了消除轨迹跟踪误差，也就是使公式（3）中的（xe，ye，θe）同时收敛到0状态，可以设计如下所示的控制律：

式中，k1，k2，k3是大于0的整数，代表待调整的控制器增益。利用公式（4）中的控制律，可以实现机器人按照预定轨迹运动的控制。

4 运动控制效果优化

对控制律（4）采用粒子群算法进行优化。粒子群算法是一种性能稳定的智能算法，具有较快的收敛速度。在机器人的运动控制中，基于粒子群算法可以对控制律（4）中的待调整增益k1，k2，k3进行优化计算。

具体计算思路如下：假设k1，k2，k3在整个实数域内的可能的取值被每一个粒子的位置所代表。这些粒子按照一定的速度运动，在运动过程中位置随时变化，表示k1，k2，k3的取值随之变化。选择轨迹跟踪误差（xe，ye，θe）的平方和作为参考指标，当参考指标的取值最小时，粒子所在的位置即是k1，k2，k3的最优解。经过反复迭代运算，最终发现，在k1=k2=k3=3时，跟踪误差（xe，ye，θe）的平方和取得最小，约等于0。因此，可以断定，k1，k2，k3的最优解为3。

5 机器人运动控制效果仿真验证

为了验证公式（4）中的运动控制律的控制效果，选择如下所示的圆形参考轨迹进行仿真验证。其中，圆形轨迹的半径为1米，机器人的初始位置为（0.5,-0.25），参考轨迹的初始位置为（0，1），初始方向角均为π/4。机器人运动控制的仿真结果如图4所示。

图4 机器人运动控制效果仿真

在图4中，黑色点表示机器人实际轨迹的初始位置，红色点表示机器人参考轨迹的初始位置。黄线和绿线分别表示参考轨迹和实际轨迹。横轴表示X坐标，单位是m，纵轴表示Y坐标，单位是m。由图4可以直观地看出，在很短的时间内，机器人的实际运动轨迹就可以收敛到参考轨迹，说明运动控制律（4）发挥了积极的作用。

为了进一步研究运动控制律的效果，分别计算出在运动过程中各个误差量的变化情况，结果如图5所示。

图5 机器人运动控制误差仿真

图5清晰地表示了在机器人运动过程中误差的变化情况。由图5可以进一步看出，在较短的时间内，运动误差Xe和Ye均稳定地收敛到0，说明运动控制律（4）具有较好的实用效果。

6 结束语

嵌入式机器人的结构相对简单，利用PLC控制器集成自主开发的控制律后，可以控制机器人按照预期的轨迹进行运动。这种控制方式可以提高机器人的应用范围。本文设计了一种控制律，并利用智能算法进行了仿真验证。结果表明，在本文设计的控制律作用下，嵌入式机器人能够按照预定的轨迹运动，进而证明了控制律的有效性。