基于改进特征点匹配的三维点云数据配准算法应用探究
吴辰 欧宇钧 朱沫
中海油能源发展装备技术有限公司深圳分公司 广东 深圳 518054
引言
随着信息技术的发展,三维激光扫描技术得到了广泛的引用,其获得的点云数据蕴含着丰富的三维数据信息。但是,受扫描范围以及目标体形状规则程度等因素的限制,一次三维扫描难以获取完整的目标体表面信息[1]。多次扫描得到的点云数据需要进行旋转、平移等处理,使其统一到标准参考系下,即实现三维点云数据的配准。
1 图像配准原理及算法
1.1 基于原理
顾名思义,图像配准指的是选择待配准图像的特定区域进行匹配,并以此转换参数为标准进行坐标系归一,通过图形融合得到所要拼接的图像。图像配准时优选位置固定的标准图像作为参考,其他待配准图像寻找到特征区域时求取转换参数。在不同条件下,受曝光度、拍摄角度等因素的影响,同一场景的照片也会存在一定的差异,为此,需要提升配准算法的精度和效率。不同图像其特征各异,各自图像的特征构成了特征空间,图像配准时两幅图像的特征空间应具有共同区域且包含足够多的图像特征,如边界、角点、轮廓等[2]。
1.2 常用算法
①模糊匹配算法。该算法选择标志区域作为模板,在待拼接图像中寻找相近区域,在匹配过程中对模板进行平移操作,计算其对应关系。模糊匹配算法实现相对简单且应用广泛,抗噪性强、配准效果好,但是随着数量级的增多,该算法计算复杂度增大,效果变差。②灰度图像配准算法。该算法利用图像中的灰度信息测量图像的相似程度,精度较高,但是容易受目标体变动、扭曲等因素的干扰。在计算过程中,该算法不需要提取图像的几何信息,其计算精度仅受图像的灰度系数影响,精度较高,但运算量较大。③相位相关算法。该算法通过参数转换将图像变换到频率域,通过傅里叶变换得到平移结果,以此为基础进行图像配准。对图像来说,傅式变换表现为图像的收缩、运动等,对噪声不敏感。④基于模型的图像配准算法。该算法基于序列图像构建数据模型,迭代求解相关模型对应的未知量并进行图像配准分析,其优点在于能够对序列图像之间的平移、收缩、扭曲等形变进行快速拼接,其统计效果较好,为实现较好的收敛效果,需要对相对准确的初始配准估计值,否则可能造成图像配准失败。⑤基于特征的图像配准算法。该算法目前在业内较为流行,通过分析待配准图像提取其特征域,将两特征域进行对应计算全局变换参数,直至匹配成功。对于待拼接图像的特征区域,优选配准效果较好的局部区域,应用矩阵配准方式求取转换参数矩阵。以局部特征为切入点实现整体图像的配准,配准速率高,其中特征提取以及算法的鲁棒性直接关系着算法的精度[3]。
2 基于特征点匹配的三维点云配准算法
基于前人研究成果,为提升点云数据配准的精度和速度,下文方法利用法向量特点检测特征点,并采用快速点特征描述直方图进行描述,筛选正确匹配点对后求解初始变换参数,最终采用基于自适应收敛阈值ICP算法进行精确匹配[4]。
2.1 基于特征匹配的初始配准
2.1.1 应用法向量提取特征点集。针对点云数据开展特征点提取时,减少点云配准的个数,能够提升配准速度。基于法向量分布特征对点云数据开展特征点提取,对于点云平坦区域,法向量变化趋势小分布密集,对于点云凸凹处,法向量变化趋势大、分布疏松。假设某点领域的点为,其对应的法向量为,其对应的协方差矩阵为下式(1),其中表示邻域质心,其中法向量C最小特征值对应的特征向量,可用特征值分解法求解。选择合适的阈值,其中法向量间的内积小于的点即为特征点。假设目标点云为P、Q,其对应的特征点集合分别为,其中m、n分别表示点云P、Q的特征点数目。
2.1.2 FPFH特征描述。一般来说,不同点云之间不存在拓扑结构关系,为此,对于前文提取的特征点来说,应进行特征描述才能确保后续特征匹配顺利开展。下文选择快速点特征直方图(Fast point feature histogram,FPFH)开展特征描述。该算法基于局部特征进行描述,以点云法线特征为目标进行估算,基于法向量信息、邻域表面曲率等信息构建直方图,通过计算配准点与领域内点法向量的夹角,得到多维度直方图,进而对其邻域内的几何特征进行描述。任选一查询点,计算点与其邻域内法向量之间的偏差。一般需要在点上定义局部坐标系,如图1所示,以期更好的计算偏差,图中d表示的是两点间的欧氏距离,计算查询点与邻域点的(),将其特征统计到11个子区间就能获取33维的直方图向量。在此基础上选择描述的邻域点,再次确认其邻域,计算其SPFH的同时加权运算得到FPFH。针对目标点集,对其各个点构建特征向量,得到特征向量点集。
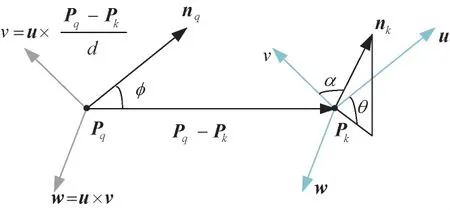
图1 局部坐标系示意图
2.1.3 双向最近邻距离比的特征匹配。根据前文所述方法,针对每个特征点都能得到其对应的特征描述,在特征向量点集中可以找到对应的匹配点。选取双向最近邻距离比作为计算准则,基于合适的阈值,舍去距离超过阈值的匹配点对,将剩余点对作为初始匹配点对。假定点云P、Q对应的特征描述集合,选择集合中描述子进行正向搜索查询,检索集合中距离描述子最近以及次近的描述子,计算的距离比,如在阈值范围内,认为为正向描述子。正向查询后,进行反向查询,即检索集合中距离描述子最近以及次近的描述子,计算与的距离比,如在阈值范围内,认为为反向描述子。如果是同一个特征点,则()为正确匹配的描述子,对应的特征点为正确的对应点对,同理查找出其他点对得到目标点云对应的点对集合,实现源点云的初始配准。
2.2 基于自适应收敛阈值的精确配准
传统意义上的ICP(Iterative ClosestPoint)算法通过迭代的方式优化不同点云之间的匹配误差,实现不同点云之间的坐标系对齐,在实际中多根据经验设定误差收敛值,下文选择基于自适应收敛阈值的ICP算法,对误差收敛值进行预算估计。以阵列激光点云为例,理想匹配的点应位于半径为(为水平分辨率)的圆内,通常情况下对应点的距离小于该值,重合点数越多,对应点之间的距离越近,配准过程中,重合点数越多说明误差越小。计算重合点数与点云总数的比值(,其中表示点云中重合的点数,表示总个数)作为加权系数,最终配准收敛误差阈值如下式(2)所示,其中为系统误差[5]。
在阐述了自适应收敛阈值ICP算法的基础上,选择源点云以及目标点云Q作为研究对象进行精准匹配,其方法主要分为以下4步:首先,基于上述初始配准得到的变换参数,针对源点云P中的点查找目标点云Q对应的最近的点,最大迭代次数定为;其次,定义分别为旋转矩阵和平移矩阵,计算变换参数(),得到所有对应点的总距离;第三,变换源点云P,重复第二步,应用上述得到的最优变换()对源点云进行变换;第四,进行点云数据配准,其对应的计算结束条件为源点云与变换后点云的平均距离不超过配准收敛误差阈值。与传统方法相比,该算法能够去除不合理的对应点对,变换关系更加准确,匹配误差更小。
2.3 实验应用效果
为验证本文方法的有效性和适用性,下文开展实验仿真方法测试。实验所用计算机芯片为Intel酷睿i7-7700,内存为16GB,软件环境为MATLAB 2018a,选择实际测量数据进行配准实验,对比分析传统ICP算法、FPFH+ICP算法以及本文算法的应用效果。本次研究选择均方根误差以及计算时间对配准精度和速度进行评估。目标模型含点共90105个,三种不同方法对应的配准结果如下表1所示,可以看出传统方法迭代次数多、配准速度缓慢,本文方法在计算精度以及速度方面优势明显,能够更好的完成点云配准,验证了该方法的有效性。

表1 点云配准结果对比
3 结束语
三维点云配准算法直接关系着工业生产测量精度的误差,是计算机科学研究的重点所在。针对传统算法计算时间长、配准精度较低的问题,本文提出的基于特征点匹配的三维点云配准算法根据点云法向量提取特征点集,基于FPFH进行点云描述,在初始配准的基础上采用自适应收敛阈值ICP算法进行精准配准,计算精度以及速度显著提升,实现了目标物体的高效配准。


