绿色金融对区域绿色经济发展的研究

潘政宇（贵州大学）

一、引言

为了达到第七十五届联合国大会上所设定的目标，中国必须不断地推动工业与能源结构的转变，以促进可再生能源的发展，力求实现经济发展与绿色转型同步进行，而这一过程离不开资金的投入。绿色金融是一种专门的金融制度，它是为了解决日益严重的资源和环境问题而生，强调了金融机构在进行资金配置决策时，应当充分考虑到与环境因素有关的潜在收益、成本和风险，从而推动国家经济和社会的长远发展，对绿色经济产生一定影响。因此，在“双碳”背景下研究绿色金融对区域绿色经济的支持作用，有利于了解二者之间的关系，找出发展绿色金融和绿色经济的方法，从而促进中国经济转型和发展，使中国经济向高质量方向发展。

二、研究设计

（一）变量选择

1.因变量

区域绿色经济（GE）难以直接观察，必须对其进行测量，但是学术界测度区域绿色经济的方法并未统一。绿色经济属于综合性经济，应从资源、环境等多个方面进行充分考虑，所以参考学者徐晓光等人（2021）的观点，利用他们构建的绿色经济发展水平指数体系，从社会发展、经济效率、创新驱动、生态建设、惠民公平共5个维度来测量区域绿色经济的发展情况。

2.自变量

目前学者们对绿色金融发展（GF）测度也有没有统一的标准，根据中国人民银行、财政部等七部委印发的《关于构建绿色金融体系的指导意见》，绿色融资是为企业提供一定资金，帮助企业减少自身对环境的污染，提高企业资源利用率，实现企业可持续发展。一方面，在传统金融概念中加入绿色发展理念，将金融发展和绿色发展相结合；另一方面要充分利用资金扶持绿色项目和企业发展，通过资本市场对资源进行优化配置，服务实体经济，促进传统产业生态化和绿色产业发展。也就是说绿色金融在促进金融发展的同时也会促进绿色发展，两者是相互影响、相互作用的，所以参考学者谢乔昕（2021）的观点，把金融发展与绿色发展的耦合协调度作为本文测度绿色金融发展水平的指标。

3.控制变量

本文的控制变量包含人均国内生产总值（Y、Y2）、外商直接投资（FDI）、对外开放程度（OP）、产业结构升级（IS）。

（二）模型构建

首先PVAR模型中的面板数据包括了时间和横截面，使数据更加丰富；其次PVAR模型没有将内外变量区别开，只将它们看作是一个内生变量，这种方式获取更多的数据特性。最重要的一点是，PVAR模型并非基于特定宏观经济概念，而是建立在现有研究基础上，对数据的时间稳定性要求又相对宽松，允许有个体效应和异方差。在观测数量较大情况下，采用的面板数据模型得到的分析结果更加可信，在本文研究中占有明显的优势。

本文运用Stata17软件对总体及不同区域进行实证研究，采用PVAR模型分析绿色金融（GF）和绿色经济（GE）的关系，构建模型如公式（1）所示。

公式中i代表了区域，这里指30个省级行政区域；t代表了代时间维度；α0代表了截距项，主要用来展现数据变化时产生的个体差异；αj代表了参数矩阵；p代表了滞后期数；yit-p代表了yit的p阶满后项；ηi代表了个体效应向量；μt代表了时间效应的向量；εit代表了随机扰动项，这里假设其服从正态分布。

三、实证分析

（一）描述性统计

在进行实证分析前需要对所有数据进行描述性统计，便于全面掌握和了解数据的情况，描述性统计结果如表1所示。

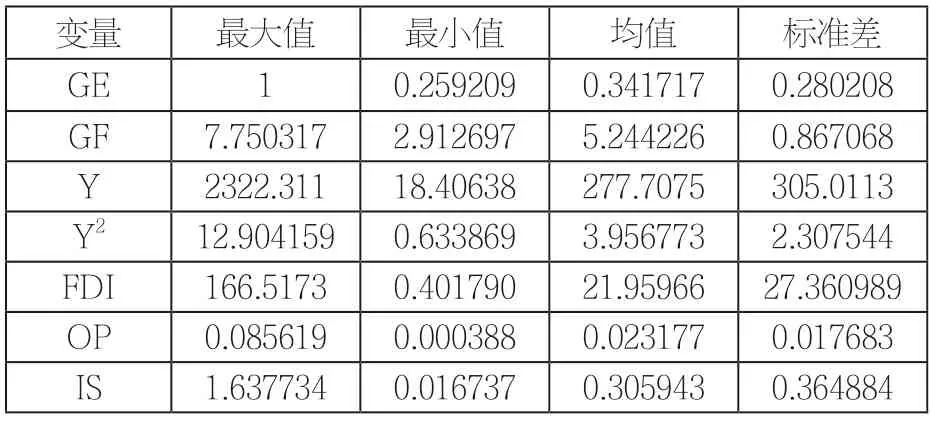
表1 描述性统计表

由表1可以看出，因变量区域绿色经济（GE）指标的最小值为0.259209，最大值为1，均值为0.341717，可见GE呈现不同的水平，各地区GE发展水平也有所不同。自变量绿色金融发展（GF）指标的最小值为2.912697，最大值为7.750317，均值为5.244226，可见各地区GF投入、发展水平都呈现巨大差距。数据的差异性可以为接下来的研究奠定良好的基础。

（二）单位根检验

为减小异方差带来的影响，在保证原始时间序列属性及相关度基础上能够得到稳定数据，本文用LLC单元根检验。首先对Y进行对数处理，再利用Stata17软件进行检验。单位根检验结果如表2所示。

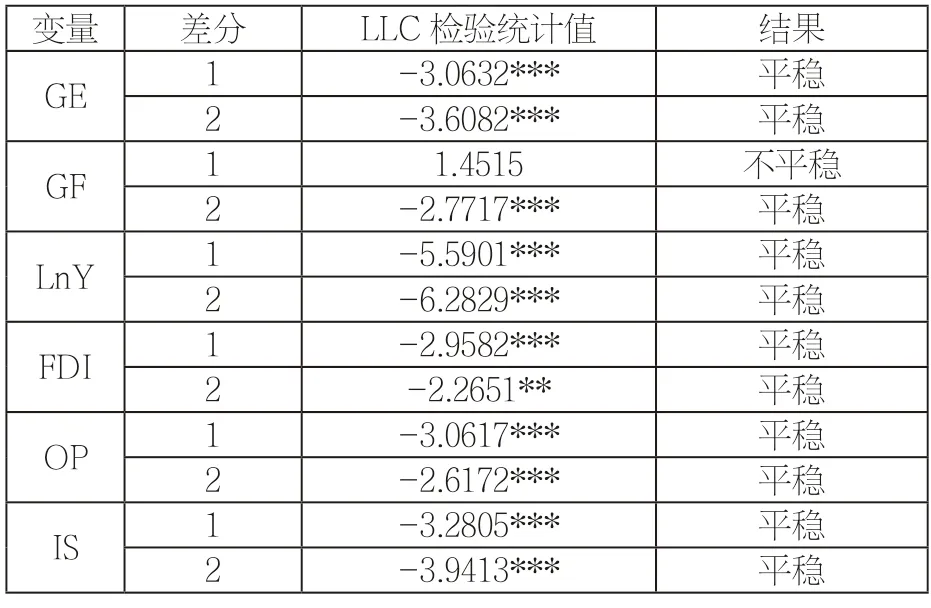
表2 单位根检验结果

由表2可以看出，各变量序列在二阶差分时均为平稳序列，属于同阶单整序列，说明各变量具有稳定性。

（三）协整检验

协整检验能够检验模型中各变量之间是否存在着长期协整关系，选取Pedroni检验、Kao检验、Westerlund检验这3种方法，以检验各变量间的长期稳定关系。在这些检验方法中，Kao检验的假设要求最强，所有面板的协整向量都要相等，Pedroni检验、Westerlund检验没有这方面的要求。协整检验结果如表3所示。

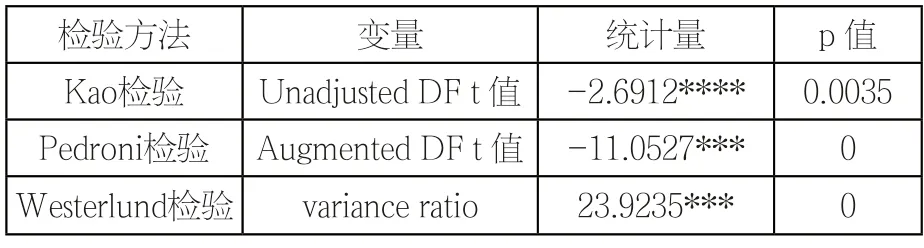
表3 协整检验结果

由表3可以看出，三种检验方法得出的P值均低于1%，故拒绝原假设，说各变量之间存在长期协整关系。

（四）滞后阶数确定

在用PVAR模型进行正式分析前还需要确定滞后期数，可以确保PVAR模型所得结果可靠。参考孙焱林、陈青青（2019）的研究，在PVAR2相关软件中构建了三个统计量，分别是AIC、BIC和HQIC，用于判断最优滞后阶数。运行结果如表4所示，最终选取了3阶滞后期。

表4 滞后阶数的选取

（五）脉冲响应分析

采用脉冲响应函数来检验随机干扰项分别对自身和其它变量的影响，由此得到对应的脉冲响应函数图，中间曲线为脉冲响应函数，两边的曲线是模拟200次得出的可信区间，红色虚线为0。全样本脉冲响应函数如图1所示。

图1 全样本脉冲响应图

对于区域绿色经济（GE）而言，当期对自身的影响相对最大，之后则是逐步降低，然后从第3期开始上升，到第4期后又开始下降，逐渐趋向于0。当GE受到绿色金融（GF）的冲击时，前两期中GE的反应迅速下降，也是从第3期开始缓慢上升到第4期，呈现向4靠近的趋势，之后再次下降。

对于绿色金融（GF）而言，在受到自身冲击的影响时，呈现出波动性发展趋势，最终逐渐收敛至0的状态。当受到GE冲击时，整体呈现出负向反应，第2期之前逐渐下降，第2期后逐步升高，第3期至第4期为正向影响，之后继续下降。

四、总结

本次研究运用PVAR模型，结合“双碳”背景分析绿色金融发展对区域绿色经济的支持作用，并通过脉冲响应分析和方差分解得到具体结果。从全样本的结果来看，区域绿色经济受到绿色金融冲击时呈波动性变化，但始终为正向影响，说明绿色金融发展对区域绿色经济具有正向支持作用。