基于动态填充和权重调整的改进DTW算法

关键词：动态规整算法；缺失值；权重调整；相似性；动态填充

中图分类号：TP311.13;U491 文献标识码：A

文章编号：1009-3044（2024）36-0067-03"开放科学（资源服务） 标识码（OSID） ：

0 引言

动态时间规整（Dynamic Time Warping， DTW） [1]算法自1994年由Berndt等人[2]提出以来，作为一种经典且广泛应用的相似性度量方法，展现出独特的优势。DTW允许时间序列间的局部弹性变换（如移位、收缩及拉伸） ，在保留单调性和边界约束的条件下，寻求全局最优对齐路径，显著增强了时间序列匹配的灵活性与精度。然而，传统DTW算法在处理复杂多变的时间序列数据时，其局限性逐渐显现[3]。核心问题在于，传统DTW算法仅聚焦于点对点之间的距离信息，而忽视了序列的整体动态特性与局部结构特征[4]。

此外，现有的一些改进尝试虽在一定程度上优化了DTW对齐效果与分类精度，但往往未能全面兼顾序列的整体趋势、分段特性及细节波动间的复杂关系，从而限制了其普适性和性能表现。在实际应用场景中，时间序列数据纷繁复杂，不同领域乃至同一序列在不同分析目标下所侧重的关键信息各不相同。例如，心电信号分析强调细节波动与局部特征的精确捕捉[5]，而水文数据则更需把握整体变化趋势[6]。单一信息维度的考量易导致算法在特定领域应用中的性能下滑。此外，噪声干扰与数据缺失作为时间序列分析中常见的挑战，进一步加剧了相似性度量的难度。传统滤波方法虽能减轻噪声影响，却可能伴随高频细节信息的损失[6]；而DTW算法在直接处理含缺失值数据时，常因数据完整性的破坏而难以准确评估序列间的相似性。

鉴于上述挑战，本文创新性地提出了MDIWDTW算法。该算法巧妙融合动态缺失值填充与权重调整机制，通过智能填充策略，有效弥补缺失数据造成的信息断层；同时，通过精细的权重分配，平衡不同特征在相似性评估中的重要性，从而实现对复杂时间序列数据更为全面、准确的相似性度量。

2 动态规整算法

2.1 DTW 算法原理

DTW算法优化了特征参数错位所产的影响，基本原理是寻找两个时间序列之间的最优弯曲路径，序列中的数据点根据坐标值去匹配另一条序列中最具有相同特点的点，数据点的距离和即为最优弯曲距离的累加和[7]。

2.2 DTW 算法的局限性

DTW算法的基本原理是寻找两个时间序列之间的最优弯曲路径，其中数据点的距离和即为最优弯曲距离的累加和。尽管DTW算法在处理非同步时间序列时表现出色，但其对缺失值表现出高度敏感性，传统的DTW算法在存在缺失值时往往无法直接应用。

当时间序列中存在缺失值时，如果直接应用DTW 算法，可能会因为缺失值而引入额外的距离或偏差，同时也可能导致序列在比对过程中出现不连续或跳跃现象，使得DTW算法难以找到最佳的对齐路径。

3 MDIW-DTW 算法框架

为了提高交通流时间序列的利用率，并更好地聚类相关的时间序列，本文提出一种基于改进DTW算法的聚类方法。该方法将着重于优化DTW算法以更好地处理时间序列中的特性，如季节性、趋势、周期性以及潜在的缺失值，同时确保聚类过程能够准确地识别出具有相似行为模式的时间序列。

3.1 算法流程

MDIW-DTW算法的实现流程如下：

第一步：预处理时间序列，随机挖空30%数据。

第二步：根据时间序列的特点，采用均值填充数据，并标记。

第三步：构建距离矩阵和权重矩阵，并初始化相关参数。

第四步：根据距离矩阵和权重矩阵计算出相似矩阵。

式中：式（7） 中的γ和δ是调整相邻点差异对权重影响的参数。这个公式的基本思想是，如果某个点与其前一个点的差异很小，那么该点在匹配过程中可能更重要。

3.2 算法复杂度分析

MDIW-DTW算法的时间复杂度主要取决于路径搜索和权重调整两个步骤。其中，路径搜索的时间复杂度为O（n^2），n为时间序列的长度；权重调整的时间复杂度取决于权重更新的频率和方式，但通常不会超过O（n）。因此，MDIW-DTW算法的整体时间复杂度仍保持在可接受的范围内。

4 实验验证与结果分析

4.1 实验数据集

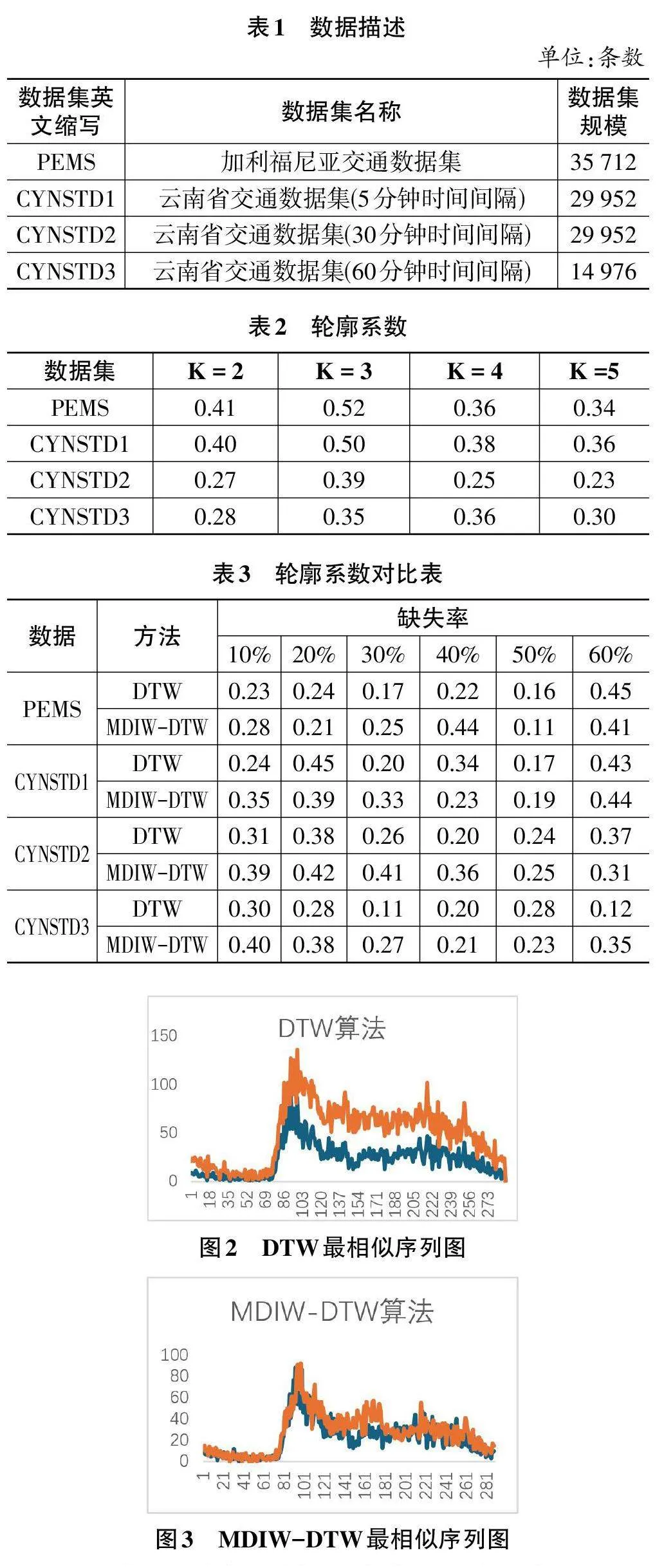
实验采用加利福尼亚高速公路网络PEMS交通流数据集和云南省交通2019年1月1日至8月26日的环路检测器采集的31天交通流数据，数据聚合周期分别为5分钟、30分钟、60分钟。数据集如表1所示。

4.2 实验设置

本实验将MDIW-DTW算法与传统DTW算法以及其他几种处理缺失值的DTW改进算法进行对比，评价指标包括相似度计算的准确性。

4.3 实验结果与分析

考虑到数据集缺失率的差异，算法相似性的度量性能也随之变化。对于不同的数据集，算法均存在其最优参数配置。本实验旨在验证MDIW-DTW算法在参数固定情况下对不同数据类型的普适性，故将参数统一设置为γ=2和δ=1。需要说明的是，本次实验设置的参数并非对所有数据集都是最优配置，在实际应用中通过选取最优参数可获得更好的相似分类结果。

本文采用K-means聚类方法，通过轮廓系数来衡量距离矩阵的聚类效果。轮廓系数取值范围为[0，1]，数值越大表明聚类效果越好。各数据集的聚类效果轮廓系数如表2所示。

根据表中数据可以看出不同的K值的选择对距离矩阵聚类效果有影响，时间间隔为5分钟的数据集相似距离聚类效果略差，当K值为4时，效果要好，时间间隔越长，每天数据量越少，距离矩阵聚类效果越好，轮廓系数越大。

本文根据DTW结合K-means对不同缺失率的时间序列进行聚类，轮廓系数表如表3所示。

由表中数据可知，MDIW-DTW算法在交通流数据集上计算相似性的表现优于传统DTW算法，不同数据集呈现出不同的聚类效果，其中在CYNSTD2数据集上效果最为显著。此外，在不同缺失率条件下，MDIW-DTW算法的距离值聚类效果始终保持优势。

图2和图3展示了缺失率为30%时的结果可视化，其中深色表示样本，浅色表示相似样本。

实验结果表明，MDIW-DTW算法在处理含缺失值的时间序列时表现出色。与传统DTW 算法相比，MDIW-DTW算法在缺失率为30%时能够更准确地计算时间序列间的相似度，并且具有更好的鲁棒性。然而，当缺失率超过30%时，算法难以有效识别相似样本。

5 结论与展望

本文提出了一种基于缺失值的动态规整算法改进方法（MDIW-DTW） ，通过动态填充缺失值并引入权重调整机制，提高了DTW算法在缺失值环境下的性能。实验结果表明，MDIW-DTW算法在处理含缺失值的时间序列时具有更高的准确性和鲁棒性。未来研究可进一步探索更高效的缺失值处理方法和权重调整策略，以提升MDIW-DTW算法的性能。同时，也可将MDIW-DTW算法推广至更广泛的应用领域。