爆炸冲击波下地应力对岩石裂纹扩展的影响

李晓静，韩雪瑞，张向阳，刘宇轩

(1.山东建筑大学土木工程学院，山东 济南 250101；2.山东轨道交通勘察设计院有限公司，山东 济南 250101)

0 引言

钻爆法因其性价比高、适应范围广，已广泛地应用于采矿、隧道建设中[1－2]。 爆炸产生的能量释放不可避免地会导致围岩破裂，尽管对爆炸引起的岩石开裂已开展了深入的研究，但是由于复杂的化学反应和昂贵的现场实验材料，其爆炸作用很难通过测量手段获取，而且随着开采深度的增加，地应力对爆炸引起的断裂影响不容忽视。

随着计算机运算能力的提升，数值软件为研究岩石的爆破提供了一种新的途径。 有限元法(Finite Element Method， FEM)[3]、 有限差分法(Finite Difference Method，FDM)[4]和离散元法(Discrete Element Method，DEM)[5]等数值模拟方法，均已广泛应用于岩体中爆破的研究。 Banadaki 等[6]通过实验室爆破试验研究了冲击波产生的钻孔周边的3 个不同裂纹区域，测量各区域力学性能和爆破压力峰值及所引起的断裂模式，并采用有限元程序AUTODYN 校准了压力和动态断裂，由数值分析所得到的断裂模式与试验结果一致。 甯尤军等[7]开发了一种不连续变形分析的方法(Discontinuous Deformation Analysis ，DDA)模拟岩石破坏问题，并有效地预测了裂缝的萌生、扩展和合并过程。 谢理想等[8]通过有限元程序LS－DYNA 数值模拟了地应力作用下的岩体爆破行，表明压力荷载作用会影响岩体损伤范围，随着地应力增大，掏槽爆破岩体的损伤范围会变小。 袁增森等[9]通过颗粒流程序(Particle Flow Code，PFC)研究了不耦合装药对花岗岩爆破损伤程度的影响，得出了随着装药不耦合系数的增大，花岗岩爆破损伤程度先增强后减弱的结果。 谢冰等[10]运用有限元软件AUTODYN 和离散元软件(Universal Distinct Element Code，UDEC)相结合的方法研究了节理几何特征对爆破的影响，并指出节理间距对预裂爆破有较大影响。 在这些方法中，虽然显式动态有限元软件可用于岩石爆破建模，但其连续性假设会使有限元难以模拟岩石中裂缝的萌生和岩石破碎，特别是对于爆炸载荷下大规模复杂裂缝的模拟。 与有限元法相比，离散元法在描述岩石微观结构和模拟岩石破裂过程方面具有明显的优势。

文章以花岗岩为研究对象，采用LS－DYNA 和PFC2D 相结合的数值分析方法，研究了爆炸冲击波对不同应力状态下花岗岩中裂纹产生和扩展的作用机理，为深部岩体爆破工程提供理论支持。

1 LS－DYNA 和PFC2D 结合数值分析方法

1.1 模拟原理

离散元相对于有限元对于解决岩石材料的破碎和裂纹的扩展具有独特的优势，因此，PFC2D 已成为分析岩体裂隙特性的强大工具。 但是，由于离散元程序PFC2D 不能模拟爆炸过程，通常爆炸波的输入要由其他方法得到，以前的学者通常采用三角形脉冲或者高斯函数曲线模拟爆炸应力波[11－12]，与真实的爆炸冲击波相比有较大的误差。 文章通过有限元软件LS－DYNA 模拟爆炸过程，通过监测孔壁附近单元，记录爆炸冲击速度，将速度转化为PFC 可兼容的数据格式，同时将速度赋予孔壁颗粒，以模拟爆炸应力波作用，观察岩体中的破碎情况及裂缝演化。 简而言之，冲击波是通过赋予粒子径向速度间接施加的。

在PFC2D 程序中，颗粒间的相互作用遵循力－位移定律和牛顿第二定律，岩石材料在PFC2D 中以刚性圆盘组合表示，圆盘之间通过接触模型粘结在一起，PB 接触模型[13]在颗粒之间可以传递力和力矩，所以人们普遍认为PB 接触模型是描述岩石微观特性的最优模型。 因此，文章所有试件的颗粒接触模型均选择PB 接触模型。 PB 接触模型基本部件和力学性能如图1 所示。

图1 PB 接触模型的基本部件和原理示意图

PB 接触模型由颗粒、线性接触和平行键3 个基本组件组成，可以承受法向力Fn、剪力Fs和弯矩M，其力学行为可认为类似于梁的。 因此，最大拉伸应力σt，max和最大剪切应力τmax分别由式(1)和(2)表示为

式中A 为粘结键横截面的面积，mm2；I 为粘结键的惯性矩，mm4；为接触颗粒中半径较小值，mm。

如果σt，max超过法向强度或τmax超过剪切强度时，平行键破坏，颗粒间的力和力矩消失，其中微裂纹代表平行键断裂的断裂，断裂的平行键处代表颗粒之间不再传递力和力矩，微裂纹的数量及位置可以反映岩体的破坏程度。

1.2 计算模型的建立

以文献[6]中的室内试验作为对比，制备直径为144 mm、高度为150 mm 的Barre 花岗岩圆柱形样品，用于实验室爆破实验，如图2 所示。 在试样中间钻取一个直径为6.45 mm 的孔作为爆破孔，将厚度为0.6 mm 的铜管紧密安装在爆孔中，采用直径为1.65 mm 的太恩(PETN)炸药及DYNO 公司的导爆索，将空气作为耦合介质进行测试，铜管的作用是防止爆生气体进入裂缝，影响对冲击波爆破作用的分析，而铜在施加的冲击载荷下容易变形，并随钻孔膨胀而不撕裂，从而防止气体渗透到产生的裂缝中。

图2 文献[6]中爆破试验样本图

在软件分析中精确还原试验的材料性质，建模过程的重点在于离散元模型的微观参数标定和爆破过程的记录方法。 使用离散元软件进行数值模拟的一个关键问题是建立颗粒的微观参数与岩石宏观力学参数之间的关系。 微观参数包括法向和剪切刚度、拉伸强度、内聚力等，使模型能够反映真实岩石试样的力学行为。 利用单轴压缩试验和巴西劈裂试验校准文献[6]中的宏观岩石参数，通过对微观参数迭代调整[14]，使模型宏观参数与实际试样参数相匹配。 实际试样巴雷花岗岩宏观力学性能参数包括密度为2.66 kg/m3、泊松比为0.16，而体积模量、剪切模量分别为25.7 和21.9 GPa，单轴抗拉强度、抗压强度分别为7.3、161.5 MPa。

岩石的单轴压缩和巴西劈裂强度模拟试样如图3 所示，采用由8 165 个颗粒组成的宽为150 mm、高为300 mm 的矩形样品用于模拟单轴压缩试验，使用895 个颗粒组成的半径为75 mm 的圆形样品用于模拟巴西劈裂试验，颗粒的半径服从均匀分布。 图3显示了花岗岩试样在单轴压缩试验和巴西劈裂试验下的应力－应变曲线，通过对比看出数值模拟得到的宏观参数与实验参数基本一致。 校准得到的岩石颗粒微观参数如下:密度为2 500 kg/m3、半径为0.9 ～1.5 mm、局部阻尼为0、孔隙度为0.16、有效模量为2.81 GPa、摩擦系数为0.7、粘结抗拉强度为85 MPa、粘结内聚力为170 MPa、刚度比kn/ks为1.5、摩擦角φ 为30°。

图3 微观参数标定曲线图

此外，在记录爆炸过程方面，由于目前无直接的方法得到炮孔壁单元速度、时程曲线，只能依托数值模拟再现爆炸过程。 而LS－DYNA 在解决非线性动力问题和有效模拟爆炸过程方面具有突出的优势。因此，采用LS－DYNA 在爆炸试验基础上建模，并根据实验构建LS－DYNA 模型，其参数根据文献[15]校准。 爆炸应力波导出及施加示意图如图4 所示。其中，炮孔模型及监测点位置如图4(a)所示。 爆炸产物压力与体积的关系利用状态方程JWL(Jones－Wilkins－Lee)描述，由式(3)表示为

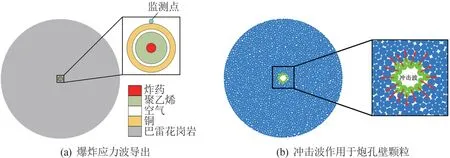
图4 爆炸应力波导出及施加示意图

式中P 为爆轰产物的压力，GPa；V 为爆轰产物的相对体积；E0为单位体积的初始比内能，GPa；A′、ω 为与炸药类型有关的材料常数；B、R1、R2均为与爆炸物类型有关的材料常数。

炸药材料参数如下:密度ρ ＝1 320 kg/m3、A′＝586 GPa、B ＝21.6 GPa、R1＝5.81、R2＝1.77、ω ＝0.282、E0＝7.38 GPa。

采用校准过的微观参数建立与现场试验相同的PFC2D 圆形岩石模型，删除中间炮孔颗粒，PFC 模型中爆炸应力波导出如图4(a)所示；将单元速度均匀地施加在爆破孔边界颗粒上，如图4(b)所示。 图5 显示了LS－DYNA 得到的爆炸后爆破孔周围单元的速度时程曲线。 具体软件操作流程图如图6所示。

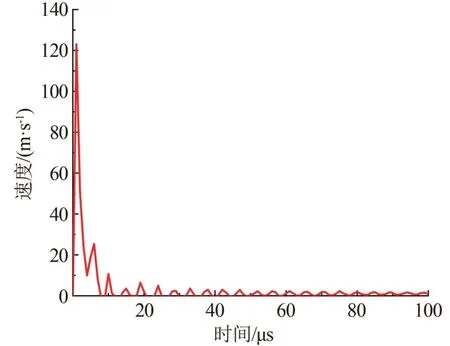
图5 爆炸后爆破孔周围单元的速度时程曲线图

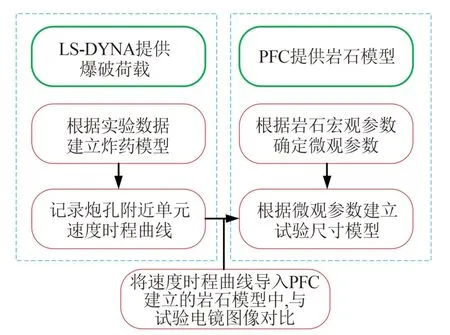
图6 LS－DYNA/PFC 联合方法流程图

1.3 有效性验证

基于LS－DYNA/PFC2D 联合分析的爆破过程中花岗岩裂纹扩展模式如图7(a) ～(e)所示，图7(f)为文献[6]中的电镜实验裂纹图。 对比选取的最终爆破与实验结果，可以看出两者吻合度较高。在炸药爆炸后，所引起的冲击波会立即作用在爆破孔壁上，爆炸释放的能量表现为从爆腔向外移动的冲击波荷载，炮孔周边的岩石动态抗压强度远小于冲击波强度，爆破孔周围的圆形区域产生了致密的拉伸和剪切裂纹，爆破孔附近首先出现了破碎区，消耗了冲击波大部分能量，破碎区内岩石主要发生剪切破坏，在PFC2D 中显示为红色裂纹，如图7(a)所示，此时炮孔周围的裂纹数量增长迅速，冲击波随着与爆破孔距离的增加而衰减为应力波，强度低于岩石的动态抗压强度，压应力波将炮孔周边岩石向外推，破碎区外形成了拉伸区，岩石在环箍方向上产生拉伸应力，远大于岩石的动态抗拉强度，拉伸区岩石主要发生拉伸破坏，在PFC2D 中显示为蓝色裂纹。由于应力波相对于冲击波波速降低，且只在几个方向产生径向拉伸裂纹，裂纹数量增速放缓，此阶段如图7(b)所示，根据裂纹时间增长曲线可知此阶段只发生拉伸破坏，当冲击波传播至自由边界处发生反射，形成拉伸波，并在岩石的边界处产生剥落裂纹，拉伸裂纹数目迅速增加，随后岩石周围的剥落裂纹与炮孔周围的拉伸径向裂纹部分贯通，形成最后的裂纹分布。 由图7(e)和(f)对比可以看出，LSDYNA/PFC 联合模型的模拟结果与试验结果吻合良好，模型能够准确模拟岩石的损伤和破坏，因此该模拟方法可以有效地应用于研究地应力与爆破荷载联合作用下岩石的裂纹扩展规律。

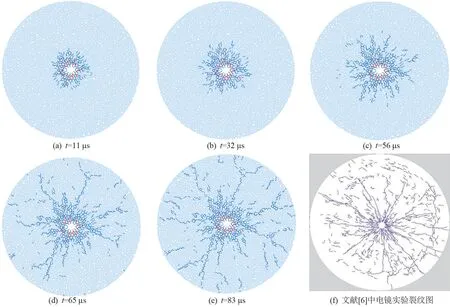
图7 岩石模拟及实验爆炸冲击波下裂纹扩展图

2 地应力对岩体爆破的影响分析

2.1 建立模型

通过1.3 节可以看出， LS－DYNA/PFC 联合模型能够准地确模拟岩石在爆破荷载下的损伤破坏情形，通过建立方形岩体模型分析地应力对爆破的影响，岩石的长、宽均为300 cm。 对模型施加应力，考虑了7 种不同的分析工况，将x、y 方向的压力Px和Py施加于模型的边界，如图8 所示，应力施加工况见表1，同时考虑到岩石尺寸，采用2 倍直径的炸药进行了研究。 通过铜管包围，记录LS－DYNA 炮孔周边的单元速度，施加在方向模型上。 在建立的数值模型中创建6 个分区，观察岩石在冲击波及应力波下的裂纹发育情况，详细记录裂纹数量的变化情况，如图8(b)所示。 1、2 区分别为贴近炮孔区与水平和竖直方向成90°的扇形区域，其半径为25 mm；紧接3、4 区位于1、2 区以外的扇形区域，其半径为100 mm；而最远处为5、6 分区，其半径为150 mm。

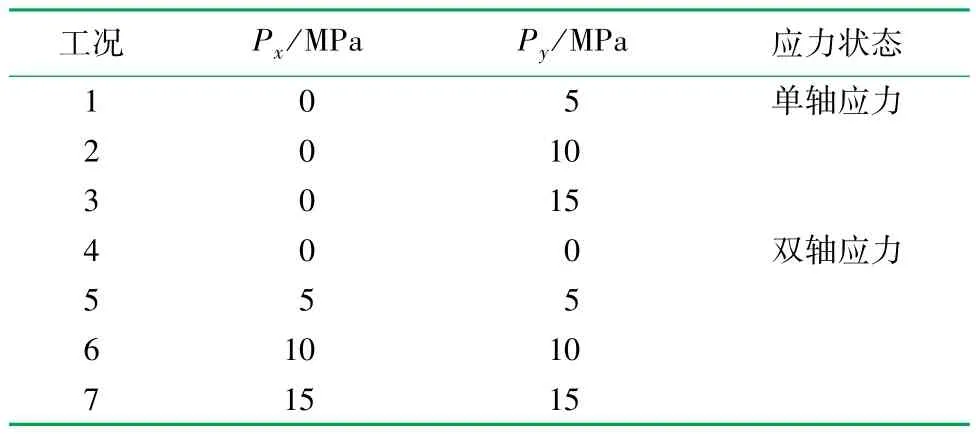
表1 不同条件下的原位应力表

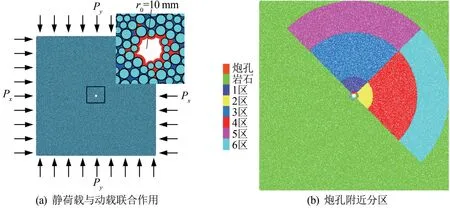
图8 PFC 模型示意图

2.2 单、双轴应力下爆炸分析

单轴应力条件下爆破作用最终的微裂纹图像如图9 所示。 爆破荷载下径向裂纹在水平方向上的扩展长度随着应力的增大而减小，垂直于主应力方向的裂纹长度随着应力的增大而增大。 图10 显示了岩石裂纹监测的分区情况，以及各个分区裂纹数目在不同应力下的对比情况。 在数值模型中创建6 个分区详细记录裂纹数量变化。 对比不同围压下各个分区裂纹数目，由于5、6 区未产生裂纹，此区域不做记录，剪切裂纹只在靠近炮孔的1、2 区产生。 通过图10(a)和(b)可知，围压对1、2 区影响较小，其裂纹数目高度重叠，由于炮孔近端冲击应力远大于地应力，地应力对破碎区域的影响较小。 如图9(c)所示，与应力垂直方向的4 区中裂纹数目随着应力增加而减小，表现为应力对裂纹的产生有抑制作用，根据图10(d)在不同应力下裂纹数目对比可知，平行于应力方向的裂纹在一定范围内会增加，应力对裂纹的产生有促进作用。 距离炮孔较远的3、4 区域裂纹显然受应力影响，地应力对裂缝数目的影响随着距爆破孔距离的增加而逐渐增加。

图9 单轴应力下微裂纹扩展分布图

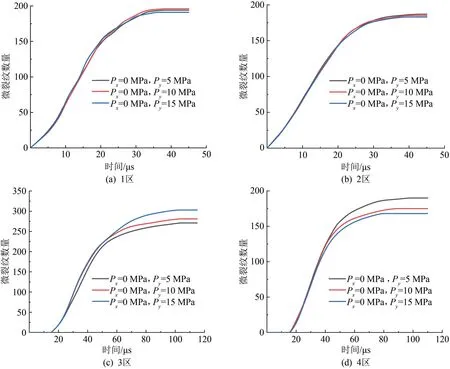
图10 不同区域单轴应力下微裂纹数量对比图

图11 为双轴应力条件下爆炸作用的裂缝最终分布情况。 随着应力的增加裂，纹长度逐渐变短，围压对拉伸裂纹影响较明显。 由于双轴应力下裂纹分布对称，所以不再分区监测，而采用总裂纹数量进行对比，如图12 所示，微裂纹数量随着应力的增加明显下降。 从裂纹数目及裂纹形状可以看出，原位应力对裂纹的发展有抑制作用。

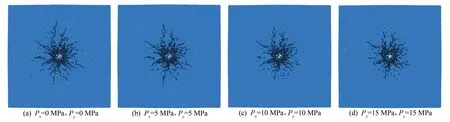
图11 双轴应力下微裂纹最终分布图

图12 双轴应力下炮孔微裂纹数量演变图

双轴应力下破碎区的形状是圆形的，炮孔周围裂纹主要由剪切裂纹和拉伸裂纹组成，随着距离的增加，几个主要裂纹从破碎区周边径向延伸，各个方向裂纹长度几乎相同，随着应力的增加，最远端径向裂纹明显长度减小，裂纹数量减少明显。 根据图12中4 种应力下裂纹数量演变过程对比可知，爆炸前期裂纹数量增长趋势相差不大，即原位应力对爆破孔周围的破碎区影响不大，随着距离炮孔距离的增加，应力对裂纹数量的影响越来越大，远处径向裂纹的延伸受到强烈抑制。

为了研究在等双轴应力和爆破荷载作用下岩石中的应力分布，在炮孔的右侧40 mm 处设置测量圆，详细分析测量圆中的动态应力响应。 岩石中某点径向应力和切向应力计算公式分别由式(4)和(5)表示为

式中σn和τn分别为正应力和切应力，MPa；σx和σy分别为x、y 轴方向的应力分量，MPa；τxy＝τyx为切向应力分量， MPa； n 为平面AB 的法线；l 和m 为应力主轴的两个方向余弦； θ 为与y 轴正向的夹角，°。任一点径向应力σr和切向应力σθ均可由式(4) 和(5) 计算得出。

在PFC2D 中，测量圆可以记录应力分量的时间曲线(x、y、τ)，测量圆中记录的应力包括静态应力和动态应力，各应力分量分布示意如图13 所示。PFC 程序中规定测量圆应力值为负时表示岩体处于压缩状态，反之处于拉伸状态；测量圆的应变速率是根据颗粒间的距离变化来测量的，应变速率为负时表示沿受力方向岩体内颗粒的平均距离变小，反之表示颗粒间平均距离变大。 通常监测点一般会出现两个峰值，即压缩应力峰值与之后的拉伸应力峰值，峰值强度由应力波的强度与初始静态应力决定，图14(a)和(b)分别显示了在等双轴应力为0、5、10 和15 MPa 时径向应力－时间和切向应力－时间曲线。从图11 可以看出，在等双轴原位应力和爆破载荷耦合下，径向压应力随原位应力的增加而上升，相反环箍向张拉应力随原位应力的增加而减小，过高的初始应力导致拉伸应力峰值低于岩石动态抗拉强度，不会造成监测区域的张拉破坏。 由此得出，在等双轴应力下拉伸裂纹被抑制，并且随着原位应力的升高，抑制效果也随之增强。

图13 岩石平面应力分布示意图

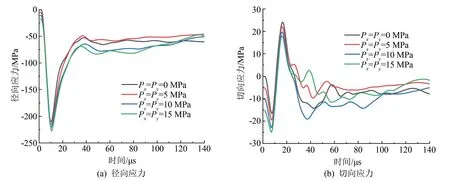
图14 不同地应力下的测点应力－时间曲线图

3 结论

文章采用LS－DYNA/PFC 相结合的方法研究爆炸冲击波下裂纹变化，模拟了冲击波引起的破碎区及裂纹区，分析了地应力在岩石爆破过程中的影响特性，得到如下主要结论:

(1) 在双轴等围压情况，微裂纹数目曲线在爆炸初期阶段高度重合，围压对破碎区影响较小，随着距离增加，裂纹数量差异将越来越明显，围压对拉伸区裂纹的扩展影响也较大；炮孔附近的径向、环向压应力均随地应力的升高而升高；预压应力增强了压缩效果，削弱了炮孔径向方向的张力效应，阻碍了裂纹扩展。

(2) 在双轴不等围压情况下，主应力的方向和大小并不会影响炮孔近端破碎区裂纹数目变化，仅影响较远端裂纹带的发展。 裂纹发展方向与单轴压力方向平行时，单轴压力促进了裂纹的形成；裂纹方向与单轴压力方向垂直时，单轴压力抑制了裂纹的形成，且随着压力的增加，其效果越明显。