铁颗粒非均相着火模型与着火特性研究

蔡 平，徐义华，胡 坤，陈宣任，杨志豪，孙海俊，任冠龙

铁颗粒非均相着火模型与着火特性研究

蔡 平，徐义华，胡 坤，陈宣任，杨志豪，孙海俊，任冠龙

(南昌航空大学飞行器工程学院江西省微小航空发动机重点实验室，南昌 330063)

基于缩小未反应核模型，考虑氧化层对氧气的扩散影响，构建了空气中Fe颗粒的非均相着火模型．模型计算的着火温度与实验着火温度的最大误差为6.95%，与Mi等的着火模型对比，两者所计算的颗粒升温速率基本一致，着火延迟时间的数量级相同．基于该模型研究了环境压强、氧气浓度、初始氧化层厚度和颗粒粒径对着火温度、着火延迟的影响．结果表明：着火温度、着火延迟时间随环境压强、氧气浓度增大而减小，随初始氧化层厚度增厚而增大；粒径小于10μm的范围内，着火温度随粒径减小而增大，粒径在10～50μm范围内，粒径对着火温度影响不大；随着粒径增加，着火延迟时间增加．

铁颗粒；燃料；非均相着火模型；着火温度；着火延迟

金属粉末具有较高的能量密度和更高的比能量，作为推进剂辅助添加剂被广泛应用于军事和商业领域[1-7]．根据金属燃料的燃烧特性可知，其产物为固态金属氧化物，属于零碳排放能源．金属粉末燃烧生成的固态金属氧化物利用太阳能等清洁能源电解冶炼可循环利用．另外，金属燃料比太阳能、风能、地热等初级能源更容易解决能源的储存、运输和交易问题，使初级能源的生产和最终用途在空间和时间上分离，从而实现世界范围内的广泛使用[8-9]．

在众多可以利用的金属燃料中，金属铁颗粒在燃烧中氧化产物直接附着在金属铁核表面，使氧化物颗粒尺寸最终大于初始铁颗粒．与镁、铝等金属的液滴蒸发气相燃烧模式相比，铁颗粒的燃烧模式，更有利于燃烧产物的回收与利用；加上金属铁在地表含量高、分布广、易开采、成本低的特点，使金属铁粉在未来有望成为一种极具潜力的零碳、清洁、可回收的绿色能源[6,8-9]．Mandilas等[10]利用铁粉燃烧特性，搭建了金属燃料内燃机，进而研究了铁粉在内燃机内的燃烧特性．刘世宁等[11]则设计出铁粉燃烧器并实现常温、常压下铁粉与空气的自持燃烧．然而，目前所设计的燃烧器因其燃烧效率低、燃烧室堵塞等问题阻碍了铁粉燃料的使用，因此需要深入理解铁颗粒复杂的着火机理，建立其着火模型，为铁粉燃烧器的科学设计、铁能源的高效利用和燃烧产物的有效回收提供一些理论依据．

当前，铁的物理化学特性已经被熟知．由于铁的熔点(1809K)和沸点(3135K)较高，常温下的铁为固态．空气中铁被氧化后主要生成+2价和+3价的铁氧化物，其中FeO和Fe3O4的熔点分别为1650K和1870K，而Fe2O3在1733K左右时会被分解为Fe3O4和O2[12]．其余氧化物也分别在3537K和2257K时被分解Fe和O2[13]．已有文献对铁的着火进行了相关的研究，高文静等[14]采用普适积分法测量出铁粉燃烧时的活化能和指前因子．孙金华等[15]通过实验发现了铁粉燃烧属于非均相燃烧，铁颗粒燃烧状态为液态．Li等[16]通过实验证明了这一点，他们测量了铁颗粒燃烧中的颗粒温度随时间的变化，发现颗粒的燃烧温度高于铁及其氧化物的熔点．Mandilas等[10]搭建了铁粉燃烧器并测量了其燃烧的温度，得到最高温度在2200～2300K，该温度高于铁熔点及其氧化物的熔点，低于铁沸点．

Leshchevich等[17]通过实验确定了铁粉着火燃烧时的活化能，并根据Arrhenius方程建立了铁粉的半经验着火模型．丁宋毅等[18]则是基于粒子群算法拟合出铁粉的燃烧速率方程，进而建立其着火燃烧模型. Schiemann等[19]认为着火反应区位于铁颗粒表面，反应产物(Fe3O4)吸附在颗粒表面，构建了铁颗粒表面反应的着火模型，该模型未考虑氧化层对着火的影响．在此基础上，Mi等[20]引入了着火反应速率与氧化层厚度呈反比关系，并基于能量守恒定律，建立了铁颗粒着火模型．

由于空气中铁颗粒的着火属于气固反应，其着火模型的建立可以参考较为成熟的冶金宏观动力模型，即缩小未反应核模型[21]．该模型指出：由于固体反应物是无孔的，初始反应仅发生在颗粒表面并形成很薄且疏松的固体产物层，气体反应物通过该产物层扩散并与固体反应物核反应．随着反应进行，产物层逐渐增厚，内部的未反应核区域逐渐缩小，直至消失．

综上所述，目前有关铁颗粒着火模型的研究主要分两种，第1种是由实验结果构成的经验公式，第2种是未考虑氧化层对氧气扩散影响的颗粒表面反应模型，或引入反应速率与氧化层呈反比的表面反应模型．然而，在铁颗粒的着火过程中，氧气在氧化层内的传输过程对颗粒着火产生一定的影响．因此，本文将基于缩小未反应核模型和谢苗诺夫着火理论，考虑氧化层内的氧气传输以及颗粒所处环境区域内的温度和氧气分布，构建空气中Fe颗粒非均相着火模型．在此基础上，应用该模型讨论环境压强、氧气浓度、初始氧化层厚度和颗粒粒径对着火温度、着火延迟的影响．

1 Fe颗粒着火模型

1.1 Fe颗粒着火过程中氧化层结构

空气中铁颗粒的着火过程，本质是铁在空气中的高温氧化过程．由文献[22-24]可知，当温度低于570℃时，Fe颗粒的氧化层由Fe3O4和Fe2O3组成的两层结构．如图1(a)所示，Fe3O4层紧挨着单质铁基体，Fe2O3层则是外氧化层．因为温度低于570℃时，FeO不稳定，其易分解成Fe和Fe3O4．当温度高于570℃时，FeO可以稳定存在，Fe颗粒氧化膜由3层氧化物组成．如图1(b)所示，FeO紧贴单质铁基体，中间层是Fe3O4，最外层是Fe2O3．但文献[25]表明，在中等温度(700～1250℃)的条件下，Fe2O3厚度占整个氧化层厚度的1%，说明Fe2O3层对氧气扩散的影响几乎为零，且生成Fe2O3的反应速率几乎为零，因此在铁颗粒着火过程中可以忽略外层Fe2O3，将氧化层视为内层为FeO和外层为Fe3O4的两层结构，如图2所示．由于着火过程中生成的氧化层厚度与粒径的比值很小，忽略Fe2O3层对计算结果几乎不产生影响．此外，这两层结构都是多孔结构，其形成机理可参见文献[26-27]．基于以上铁的高温氧化机理以及氧化层的结构构建铁颗粒着火模型．

（a）温度低于570℃

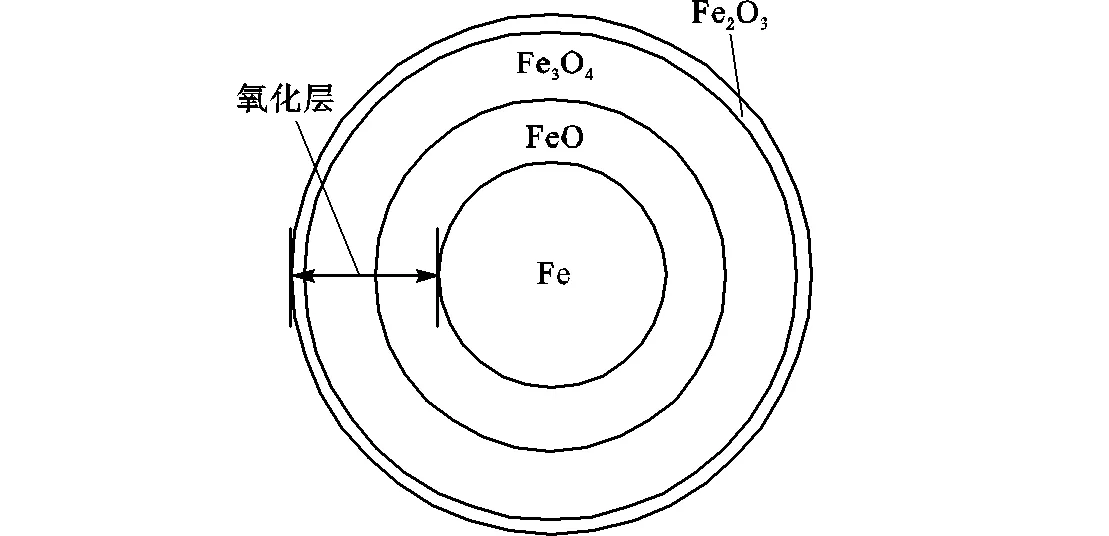
（b）温度高于570℃

图1 颗粒的氧化层结构

Fig.1 Oxide layer structure of particle

图2 不考虑Fe2O3层时颗粒的氧化层结构

1.2 着火机理

由于铁颗粒着火过程较为复杂，影响着火因素较多，为了简化着火模型，对整个着火过程做出如下假设：

(1)颗粒为球形且内部温度均匀．因为颗粒尺寸极小且内部传热速度很大．

(2)着火过程中，不考虑多孔氧化层内部的化学反应，反应区位于铁核与氧化层界面上．

(3)双层氧化层结构可以近似简化为单层结构．因为在FeO层内，Fe与O的摩尔比接近1，且中等温度下摩尔比随温度变化而在0.84～0.95内变动．此外，在FeO层存在较多Fe3O4聚集区[28]，可以认为FeO层主要由Fe和Fe3O4构成．需要说明的是，这种近似简化会导致计算的反应放热速率比实际略大．因为生成FeO的反应热小于生成Fe3O4的反应热，将氧化层简化后，使原本一部分氧化成FeO的Fe直接氧化成Fe3O4．

(4)在颗粒升温过程中，不考虑颗粒受热膨胀，也不考虑a-Fe到g-Fe再到δ-Fe的相变过程，因为相变潜热远小于反应放热，用于计算铁的热力学性质采用α-Fe的热力学性质．

(5)在整个着火过程中，颗粒仅与氧气反应，其他气体称为惰性气体．颗粒处于相对静止、干燥的环境中．

(6)为1，即＝ρcD．

基于以上假设，将着火区域分为内部未反应铁核(Ⅰ区)、多孔Fe3O4氧化层(Ⅱ区)和空间环境(Ⅲ区)，如图3所示．空气中的O2先从环境传输至颗粒表面，再通过多孔Fe3O4氧化层扩散到铁-氧化层界面上，并与Fe反应生成Fe3O4，如式(1)所示．反应产物堆积在氧化层内表面，使氧化层朝颗粒内部方向逐渐增厚，未反应铁核区不断缩小．

此外，有两种热源使颗粒升温，一是外部环境热量通过导热和热辐射方式传输至颗粒，二是反应热．

图3 铁颗粒着火模型原理示意

1.3 着火控制方程

依据上述着火机理，着火控制方程可简化为径向一维球坐标描述，以铁颗粒的中心为坐标原点，建立球坐标系，如图4所示．由图可知，氧气通过浓度梯度在区域Ⅲ和Ⅱ中扩散．

1.3.1 空间区域Ⅲ的控制方程

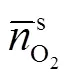
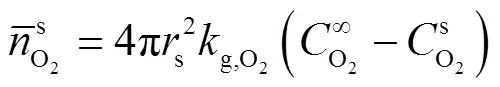
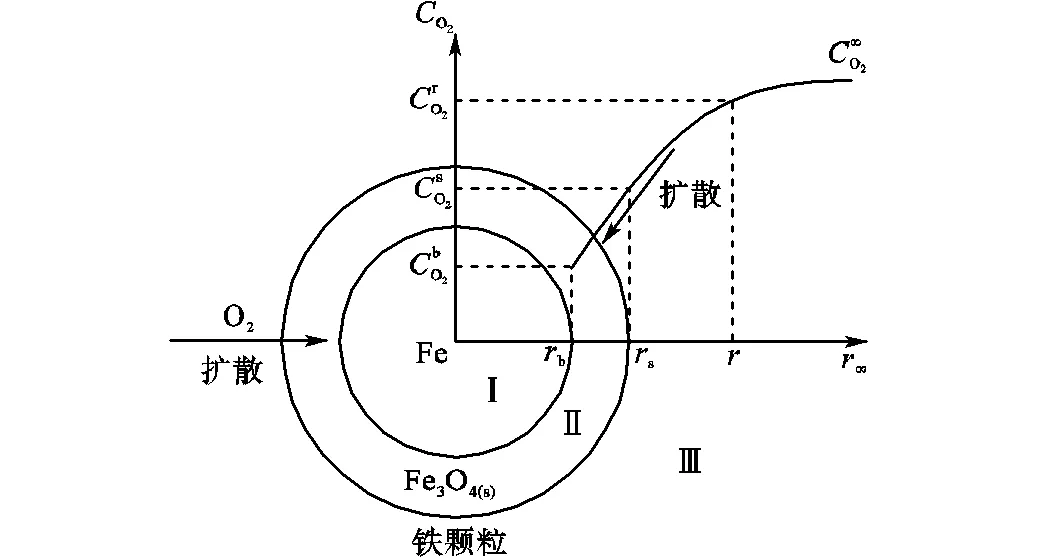
图4 球坐标系下的氧气浓度分布

颗粒处于稳定状态，依据控制体内能量增量等于外界传入的热量，可获得空间区域的能量方程，如式(5)所示．

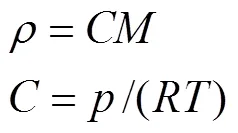
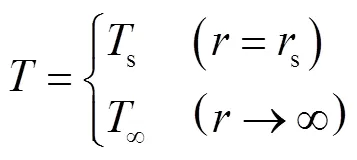
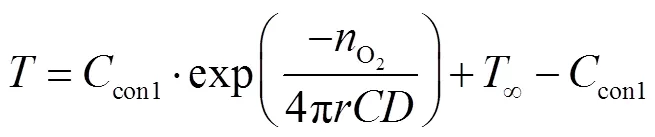
1.3.2 氧化层区域Ⅱ的控制方程

由于氧化层为多孔结构，考虑多孔结构对氧气扩散影响，引入氧化层的孔隙度p和孔隙的曲折度p两种参量[29]．其中孔隙度为孔隙空间占整个氧化层的体积比值，一般是小于1的正数；而曲折度是大于1的数，因为氧化层内的孔径远大于反应物分子的平均自由程，同时孔的走向是蜿蜒曲折的，迫使反应物在孔内传输路径要比直线传输长．此外，文献[30]表明，孔隙度与曲折度呈反比关系且乘积为1．

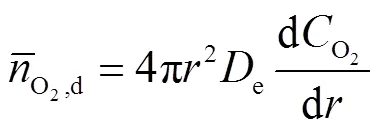
依据着火机理，颗粒内部的化学反应是不可逆的，且反应物Fe为固态，反应速率由O2的浓度及其化学动力学机理决定．依据化学速率由反应物浓度控制的质量作用定律，采用O2的消耗速率来表示反应速率，如式(9)所示．化学反应速率常数(re1)可用Arrhenius函数描述[31]，即

在稳态条件下，氧气扩散速度等于反应速率，即

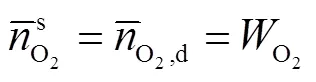
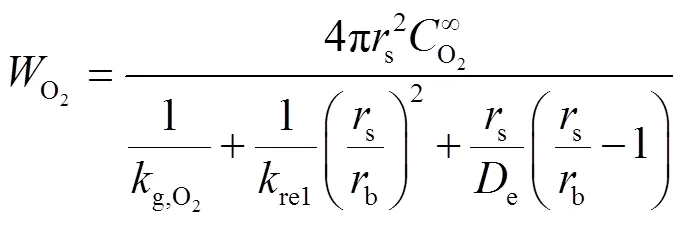
1.3.3 氧化层内径及颗粒温度的控制方程

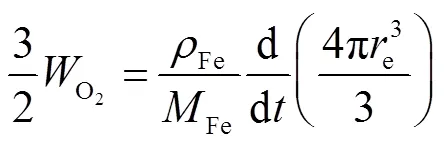
联立方程(11)和(12)得到氧化层内径与时间的变化关系，如式(13)所示．

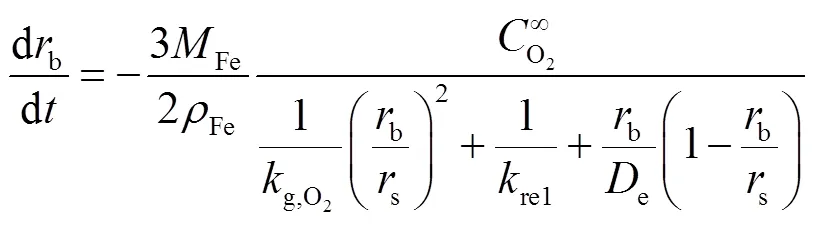
依据能量守恒关系，得到颗粒温度s与时间关系式，即

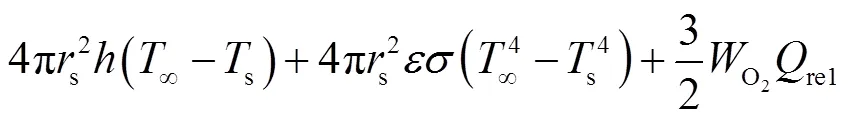
式(14)中等号右边第1项为对流换热，第2项为辐射传热，第3项为反应热．

2 计算结果与分析

2.1 数值计算方法

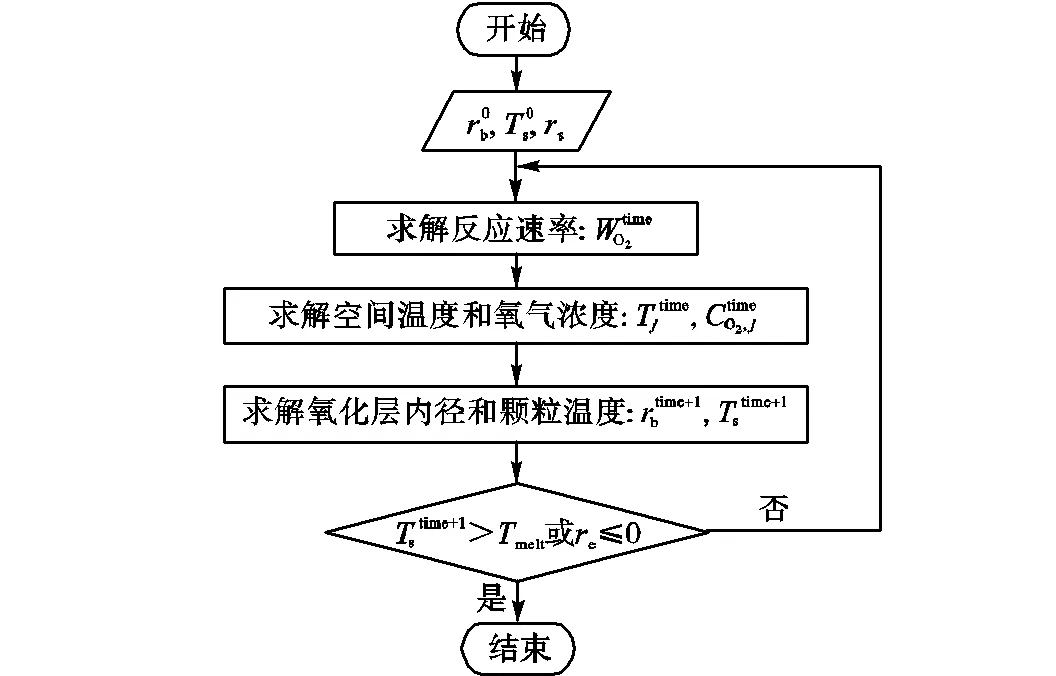
图5 数值计算流程

2.2 模型校核

Arshad等[32]利用Godbert-Greenwald (G-G)加热炉构建了铁粉的着火温度测量系统．该测量系统用于观察铁粉在某一环境温度下是否被点燃．如果铁粉可以在一定的最低环境温度下点燃，认为该环境温度为着火温度且这种测量法是依据谢苗诺夫着火理论[31]．他们利用该系统测量出不同环境压强下粒径为32～50μm、质量浓度为370g/m3的铁粉的着火温度，结果如表1所示．

表1 不同压力下铁粉在空气中的实验着火温度[32]

Tab.1 Experimental ignition temperature of iron powder in air with different pressures[32]

对于表1中的所有实验工况，使用本文所建立的着火模型来计算和分析它们的着火过程．其中模型计算采用的颗粒直径为实验粒径的平均值，即＝41μm．通过模型计算可以得到着火过程中颗粒温度与时间的关系．以该表的工况1为例，绘制了不同环境温度下，颗粒温度随时间的变化关系，如图6所示．当环境温度T≤867K时，颗粒的最高温度停留在环境温度附近．一旦将环境温度提升至868K，那么颗粒温度在0.34s左右时突破环境温度，且急剧升高．说明此时的铁颗粒已经着火成功，因此把环境温度868K作为铁颗粒的着火温度．

图6 不同环境温度下颗粒温度随时间变化

其他工况所计算的着火温度如表2所示．由该表可知，模型计算的结果与实验结果误差均小于7%．另外，计算着火温度的变化趋势与实验结果相反，因为Arshad等往加热炉内通入了常温空气．点燃铁粉的同时，炉内的空气也会被加热．随着炉内压强的增大，通入的空气增多，要使铁粉在3s内被点燃，需要提高炉内温度．

表2 计算着火温度与实验着火温度对比

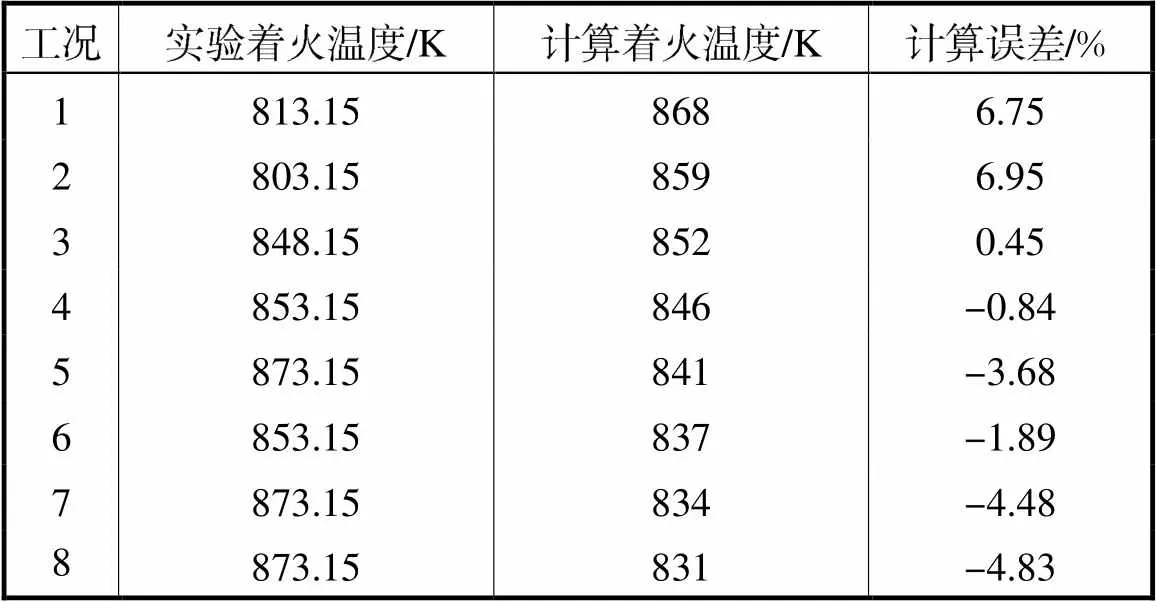
Tab.2 Comparisonbetween calculated ignition tempera-ture and experimental ignition temperature

为了进一步说明着火模型的特点，将本模型与Mi等[20]的着火模型进行对比．在Mi模型中，Mi认为Fe离子在氧化层中的传输性能比O离子强，氧化层的生长主要受Fe离子向外扩散控制，内部铁核缩小的同时，氧化层向外增厚，其构建的反应速率与氧化层厚度呈反比关系．设铁颗粒半径s＝250nm，初始氧化层厚度为3nm，初始颗粒温度298.15K，在环境温度T＝1100K、压强p＝101325Pa、氧气占比为21%的干燥空气中的条件下，分别利用本文模型和Mi模型进行数值计算，得到两种模型下颗粒温度随时间变化，如图7所示．由图可知，在铁颗粒着火之前，两者所计算的颗粒温度随时间变化的趋势一致，着火延迟时间分别是5.65μs和8.83μs，两者着火延时时间的数量级相同．

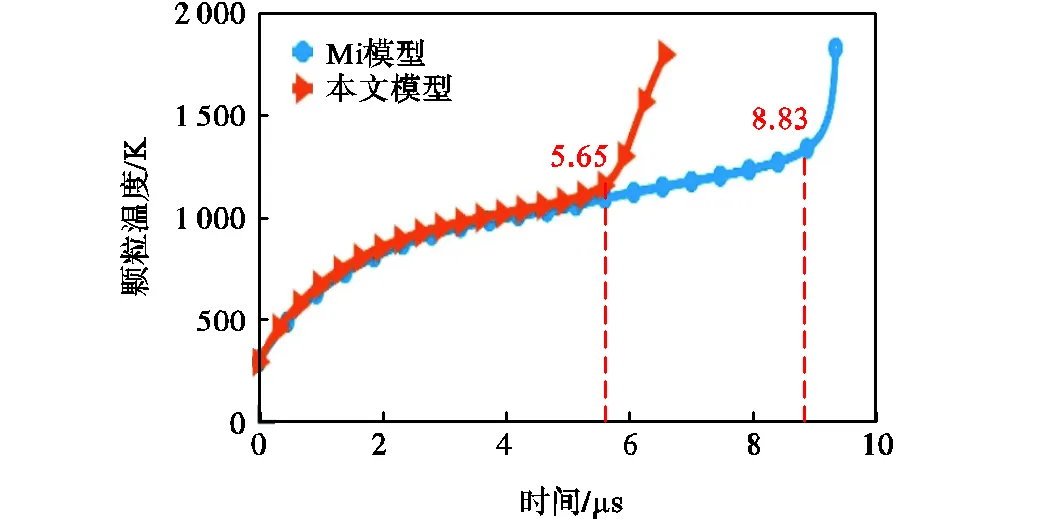
图7 Mi模型和本文模型所计算的颗粒温度随时间变化

2.3 着火过程参数分析

设铁颗粒半径s＝250nm，依据文献[10，33]可取其初始氧化层厚度为3nm，则其初始氧化层内径b＝247nm，初始颗粒温度298.15K，在环境温度T＝1000K、压强p＝101325Pa、氧气占比为21%的干燥空气中的条件下，通过数值计算得到氧化层内径和颗粒温度随时间变化(见图8)，以及在不同颗粒温度时所对应的空间温度分布(见图9)和空间氧气摩尔浓度分布(见图10)．其中对于空间距离采用＝/s，对空间坐标进行无量纲化．

由图8可知，随着反应时间增加，颗粒升温分为3个阶段，即颗粒在对流换热作用下的急剧升温阶段(时间小于5μs)、颗粒温度接近环境温度的缓慢升温阶段(时间在5μs至16μs之间)，以及着火后的颗粒快速升温阶段(时间大于16μs)．反应产物堆积在氧化层内表面，氧化层的厚度可由其内径表示，厚度增大，则内径减小．由该图可知，随着反应时间增加，氧化层内径先缓慢减小，在16μs时，由于颗粒已经被点燃，内径开始急剧减小，即氧化层厚度快速增大．

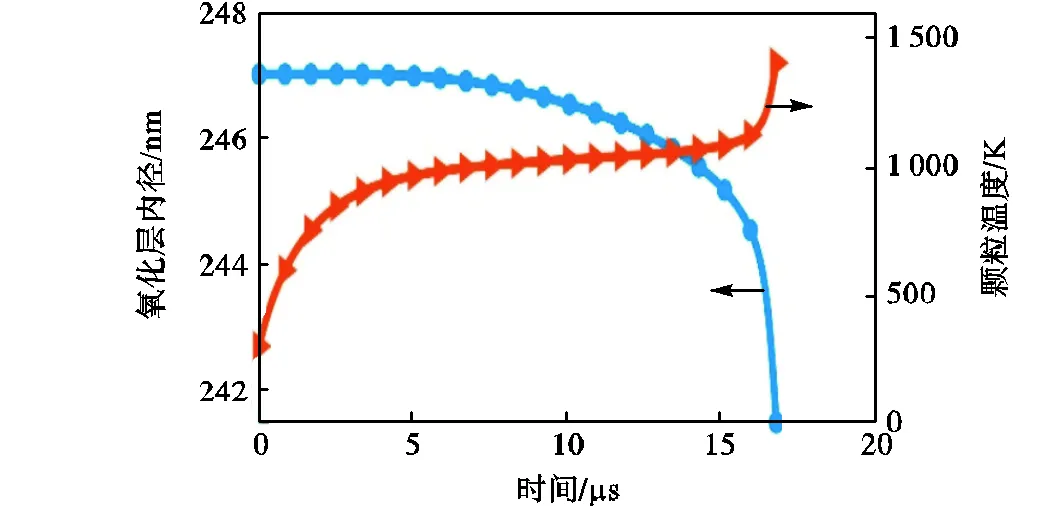
图8 氧化层内径和颗粒温度随时间变化

由图9和图10可知，在时间从0ms增加至7.5μs过程中，由于颗粒温度始终不超过环境温度(1000K)，铁颗粒所处的空间区域中，随着空间距离的增加，空间温度的走向可分为两部分，即空间温度急剧增大(距离/s小于4左右)，以及其缓慢增大(距离/s大于4)．在此过程内，反应速率主要受化学动力学控制，随着时间增加，颗粒温度升高，反应速率有微小增加，使颗粒周围的氧气摩尔浓度微量减小．在着火过程的7.5μs至16.0μs中，由于颗粒温度高于环境温度，空间温度随空间距离的增加而逐渐减小．此过程中，颗粒温度接近着火温度，氧气在空间区域(Ⅲ区)和氧化层(Ⅱ区)中的扩散效应比前一过程明显，随着时间增加，颗粒的反应速率受化学动力学控制逐步过渡到受化学动力学与氧气扩散机制共同控制，且反应速率有较大增加，使颗粒周围的氧气摩尔浓度有了较大的减小；随着空间距离的增加，氧气浓度先急剧增大(距离/s小于4左右)，再缓慢增大(距离/s大于4)．此外，当空间距离足够大时，空间温度和氧气浓度都趋于环境值．

（a）氧气摩尔浓度分布

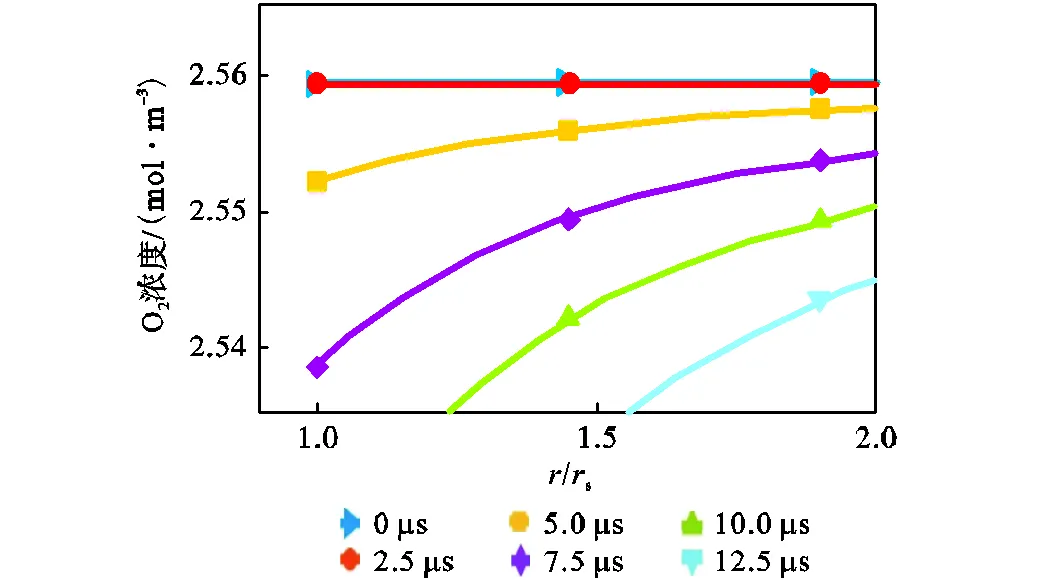
（b）图(a)中局部放大

图10 不同时刻下的氧气摩尔浓度分布

Fig.10 O2molar concentration distribution under differ-ent time

为了更加直观体现铁颗粒着火过程中的空间参数变化规律，图11给出了不同时刻的温度分布和氧气摩尔浓度分布云图．图11(b)中间白色部分为颗粒．由图11可知，在着火过程中，随着时间增加，在离开颗粒方向的空间温度梯度由正梯度逐渐转变为负梯度，即随着着火时间的推移，颗粒温度由常温开始迅速增大到接近环境温度，再在反应生成热作用下颗粒温度进一步升高，直至着火成功；而氧气摩尔浓度梯度在离开颗粒方向保持正梯度，且梯度随时间的增加而增大．

2.4 环境压强、氧气浓度、初始氧化层厚度和颗粒粒径对着火温度的影响

2.4.1 环境压强的影响

设铁颗粒半径s＝250nm，初始氧化层内径b＝247nm，初始颗粒温度298.15K，在氧气占比为21%的干燥空气中的条件下，计算了环境压强为0.05～0.5MPa的着火过程，得到了着火温度随环境压强的变化，如图12所示．由图可知，着火温度随环境压强增大而降低，因为环境压强与浓度呈正比，随着环境压强增大，氧气浓度增加，增大了着火过程的颗粒反应速率，使单位时间内反应热增多，降低了着火温度.

（a）温度

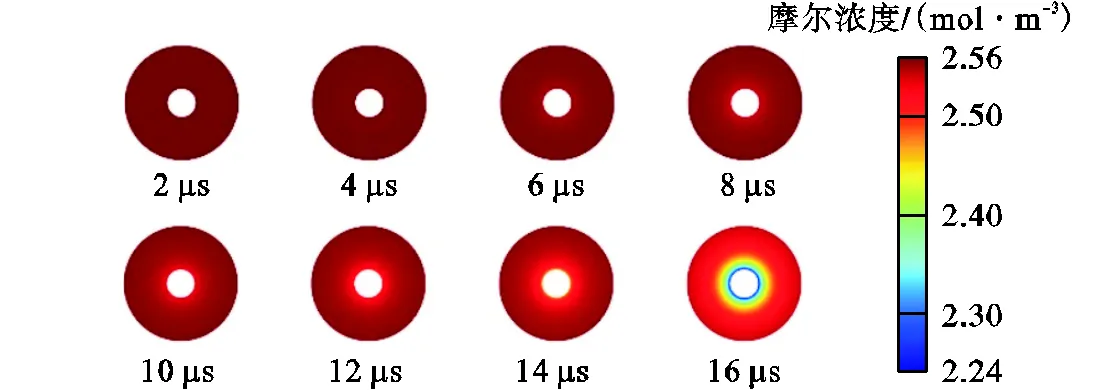
（b）氧气摩尔浓度

图11 着火过程中空间参数分布

Fig.11 Space parameter distribution during ignition

图12 着火温度随环境压强的变化

Fig.12 Ignition temperature versus atmospheric pressure

2.4.2 氧气浓度的影响

设铁颗粒半径s＝250nm，初始氧化层内径b＝247nm，初始颗粒温度298.15K，在压强p＝101325Pa干燥气氛中的条件下，由于压强不变，要改为氧气浓度则只需改变氧气摩尔分数，设气氛中氧气的摩尔分数从0.21均匀变化到0.66，计算得到的着火温度随氧气摩尔分数的变化如图13所示．由图可知，着火温度随氧气浓度增大而减小．

2.4.3 初始氧化层厚度的影响

设铁颗粒半径s＝250nm，初始颗粒温度298.15K，在压强p＝101325Pa、氧气占比为21%的干燥空气中的条件下，计算了初始氧化层厚度为0～45nm的着火过程，得到了着火温度随初始氧化层厚度的变化，如图14所示．由图可知，着火温度随初始氧化层厚度增厚而增大，因为随着氧化层厚度增大，阻碍了氧气的扩散，铁颗粒反应速率降低，需要更高的环境温度弥补颗粒升温速率，使其达到成功着火温度．

图13 着火温度随氧气摩尔分数的变化

图14 着火温度随初始氧化层厚度的变化

2.4.4 颗粒粒径的影响

设铁颗粒初始氧化层厚度3nm和初始颗粒温度298.15K，在压强p＝101325Pa、氧气占比为21%的干燥空气中的条件下，计算了颗粒直径为100nm至50μm的着火过程，得到了着火温度随颗粒粒径的变化，如图15所示．由图可知，粒径在100nm到10μm左右，着火温度随粒径增大而显著减小，因为反应速率遵循线性规律，导致着火温度与颗粒尺寸有关[34]．对于等质量的纳米级颗粒群[35]，其着火规律与单颗粒相反，即由于纳米颗粒群效应可大大降低其着火温度，随着粒径减小，比表面积增大，颗粒的着火温度降低．在粒径为10μm至50μm之间，着火温度随粒径增大而稍有降低，可以认为该粒径范围内，粒径对着火温度的影响较小．

图15 着火温度随颗粒直径的变化

2.5 环境压强、氧气浓度、初始氧化层厚度和颗粒粒径对着火延迟的影响

基于控制变量法，将研究环境压强、氧气浓度、初始氧化层厚度和颗粒粒径对着火延迟的影响．其中，着火延迟时间为颗粒从初始状态到颗粒温度开始急剧上升时的时间变化量，即着火时刻的时间量为着火延迟时间．

2.5.1 环境压强的影响

设铁颗粒半径s＝250nm，初始氧化层内径b＝247nm，初始颗粒温度298.15K，在温度T＝1100K、氧气占比为21%的干燥空气中的条件下，计算了环境压强为0.05～0.5MPa的着火过程，得到了不同环境压强下颗粒温度随时间的变化，如图16所示．由图可知，在颗粒着火成功之前，不同环境压强下，颗粒温度随时间变化的趋势基本不变，即环境压强对颗粒升温速率几乎没有影响，因为着火过程中颗粒温度不高，反应热比较小，颗粒升温所需的能量主要来自环境对颗粒的加热．在环境压强为0.05MPa、0.10MPa、0.15MPa、0.30MPa和0.50MPa的条件下，所计算的着火延迟时间分别为7.1μs、5.7μs、5.1μs、4.5μs和4μs，说明着火延迟时间随环境压强增大而缩短，这主要因为颗粒温度达到着火临界点温度后，其反应速率受化学动力学与扩散机制共同控制，则环境压强越大，氧气浓度越高，使得其反应速率增大，放出的反应热增多，从而减少颗粒达到着火点的时间．

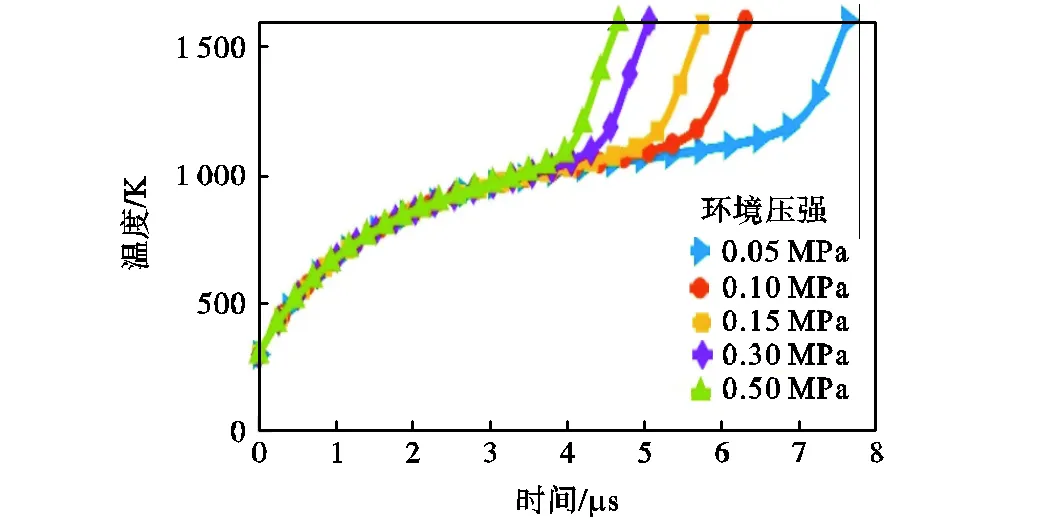
图16 不同环境压强下颗粒温度随时间变化

2.5.2 氧气浓度的影响

设铁颗粒半径s＝250nm，初始氧化层内径b＝247nm，初始颗粒温度298.15K，在压强p＝101325Pa、温度T＝1100K干燥气氛中的条件下，计算了氧气摩尔分数为0.21～0.66的着火过程，得到了不同氧气摩尔分数下，颗粒温度随时间的变化，如图17所示．由图可知，在着火成功之前，不同氧气浓度下，颗粒温度随时间变化的趋势基本不变，即氧气浓度对颗粒升温速率几乎没有影响．在氧气摩尔分数为0.21、0.26、0.31、0.46和0.66的条件下，所计算的着火延迟时间分别为5.7μs、5.4μs、5.1μs、4.7μs和4.3μs，说明着火延迟时间随氧气浓度增大而缩短，这与环境压强的影响相似，所导致的机理也相同.

图17 不同氧气摩尔分数下颗粒温度随时间变化

2.5.3 初始氧化层厚度的影响

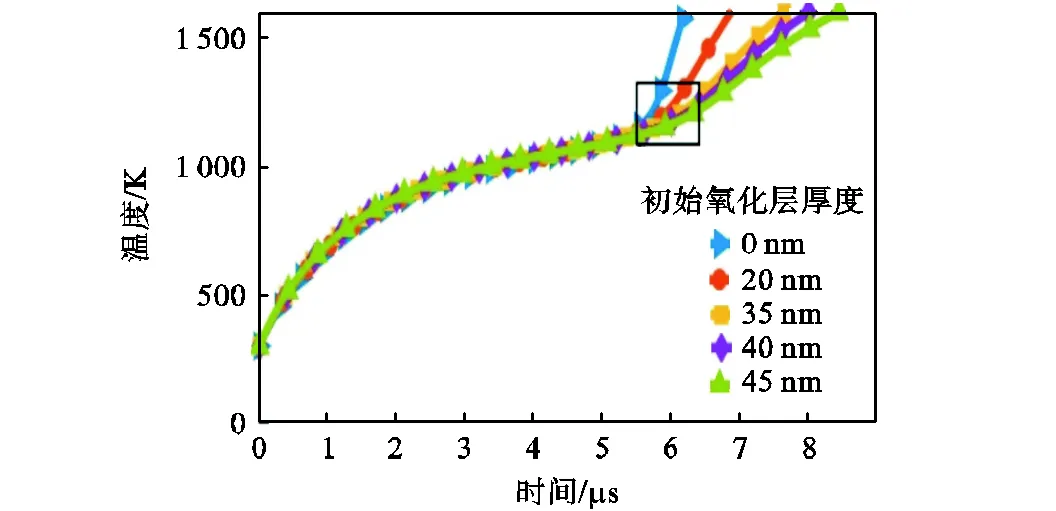
设铁颗粒半径s＝250nm，初始颗粒温度298.15K，在压强p＝101325Pa、温度T＝1100K、氧气占比为21%的干燥空气中的条件下，计算了初始氧化层厚度为0～45nm的着火过程，得到了不同初始氧化层厚度下，颗粒温度随时间变化，如图18所示．由图可知，在着火成功之前，不同初始氧化层厚度下，颗粒温度随时间变化的趋势基本不变，即初始氧化层厚度对颗粒升温速率几乎没有影响．在初始氧化层厚度为0、20nm、35nm、40nm和45nm的条件下，所计算的着火延迟时间分别为5.6μs、5.9μs、6.1μs、6.2μs和6.3μs，说明着火延迟时间随初始氧化层厚度增厚而增加，因为颗粒温度达到着火临界点温度后，反应速率受化学动力学与扩散机制共同控制，随氧化层厚度增厚，氧气扩散速率减少，反应速率减小，增加了颗粒达到着火点的时间．

2.5.4 颗粒粒径的影响

设初始氧化层厚度3nm、初始颗粒温度298.15K，在压强p＝101325Pa、温度T＝1100K、氧气占比为21%的干燥空气中的条件下，计算了颗粒直径为100～3000nm的着火过程，得到了不同粒径下，颗粒温度随时间变化，如图19所示．由图可知，在着火之前，不同颗粒粒径下，颗粒温度随时间变化的趋势变化较大，且随着粒径增大，颗粒升温速率减小．这主要因为粒径越大，颗粒存储能量越多，环境对颗粒的加热时间增加．在颗粒直径为100nm、500nm、900nm、1500nm和3000nm的条件下，所计算的着火延迟时间分别为0.45μs、5.9μs、16μs、40μs和142μs，说明随着粒径增大，着火延迟时间增加．

（a）颗粒温度变化

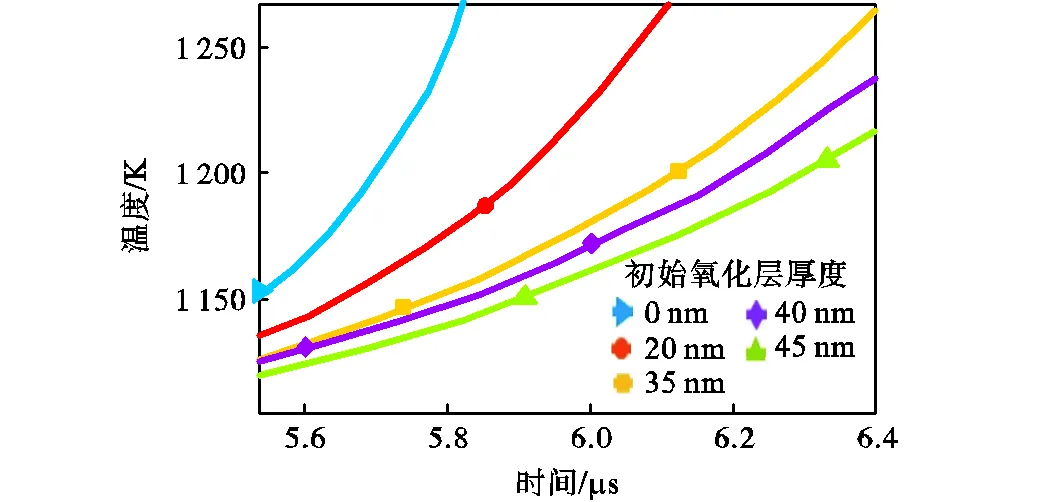
（b）图(a)的局部放大

图18 不同初始氧化层厚度下颗粒温度随时间变化

Fig.18 Particle temperature versus time under different initial oxide-layer thickness

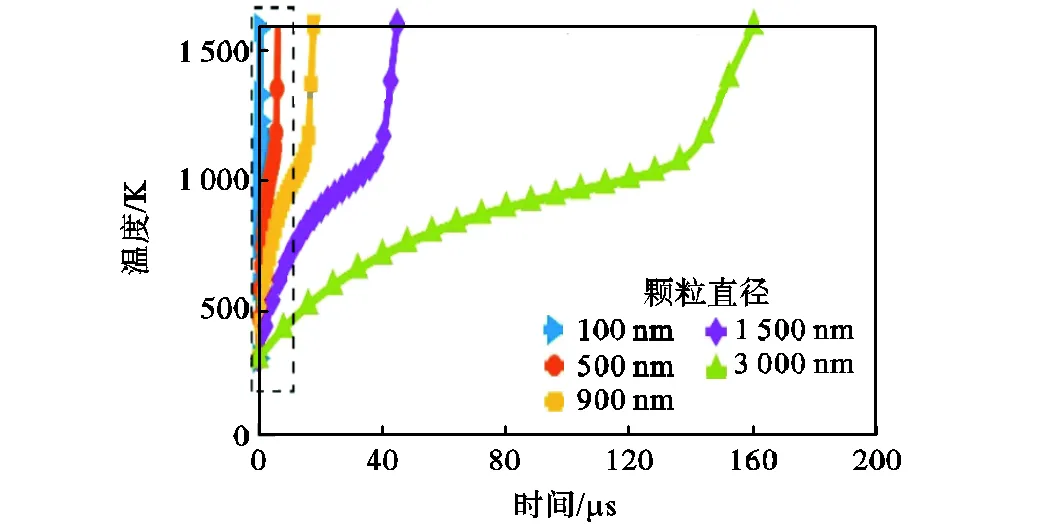
（a）颗粒温度变化

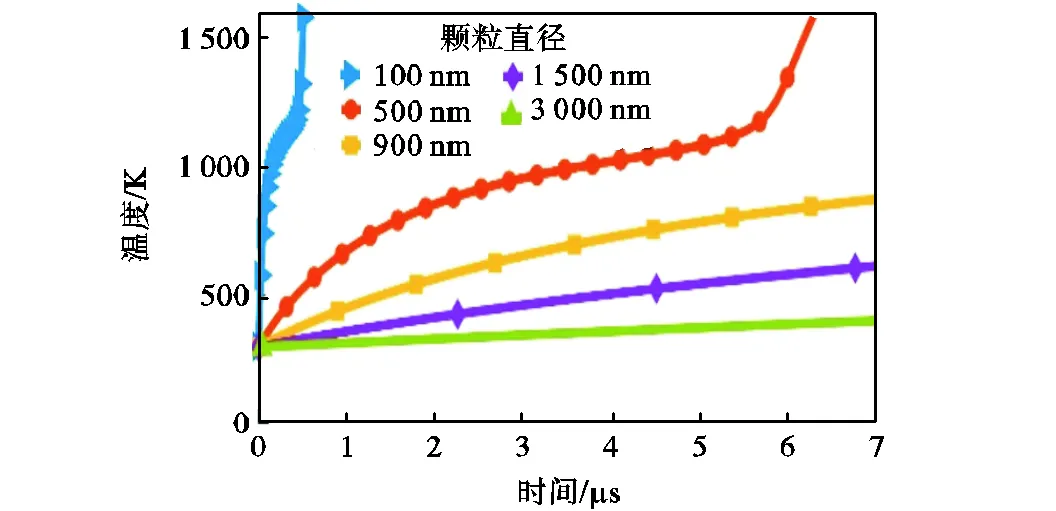
（b）图(a)的局部放大

图19 不同颗粒直径下颗粒温度随时间变化

Fig.19 Particle temperature versus time under different particle diameter

3 结 论

基于缩小未反应核模型，假设氧化层为单层Fe3O4层，并考虑氧化层对氧气扩散的影响，构建了空气中Fe颗粒的非均相着火模型．应用该模型与Mi模型的计算结果进行对比，分析了铁颗粒着火过程中颗粒温度、氧化层内径随时间变化关系及着火过程中不同时刻的铁颗粒所在空间的温度和氧气摩尔浓度分布．基于该着火模型，研究了环境压强、氧气浓度、初始氧化层厚度和颗粒粒径对着火温度、着火延迟的影响，得到如下结论：

(1)所建立的着火模型计算的着火温度与实验结果的最大误差为6.95%，与Mi模型所计算的颗粒升温速率基本一致，两者着火延迟时间的数量级相同．

(2)在铁颗粒所处的环境空间中，随着时间增加，在离开颗粒方向的空间温度梯度由正梯度逐渐转变为负梯度，即随着时间的推移，颗粒温度由常温开始迅速增大到接近环境温度，再在反应生成热作用下颗粒温度进一步升高，直至着火成功；而氧气摩尔浓度梯度在离开颗粒方向保持正梯度，且梯度随时间的增加而增大．

(3)在颗粒着火成功之前，颗粒升温速率受环境压强、氧气浓度和初始氧化层厚度的影响较小，但随颗粒粒径增大而减小．

(4)着火温度随环境压强和氧气浓度增大而降低，随初始氧化层厚度增大而升高；粒径小于10μm的范围内，着火温度随粒径减小而增大，粒径在10～50μm范围内，粒径对着火温度影响不大．着火延迟时间随环境压强、氧气浓度增大而缩短，但随初始氧化层厚度、颗粒粒径增大而延长．

1——指前因子，s-1；

和C——混合气体和组分的摩尔浓度，mol/m3；

和e——扩散系数和多孔氧化层的扩散系数，m2/s；

1——活化能，J/mol；

——对流换热系数，W/(K·m2)；

re1——化学反应速率常数；

和M——混合气体和组分的相对分子(原子)质量，g/mol；

——环境压强，Pa；

re1——反应热，J/mol；

——通用气体常数，J/(mol·K)；

、e、b和s——半径、颗粒内部Fe核半径、氧化层内径和颗粒半径(氧化层外径)，m；

——舍伍德数；

、melt、s和T——温度、Fe的熔点、颗粒温度和无穷远处的温度，K；

——速度，m/s；

——颗粒表面的发射率；

p——多孔氧化层的孔隙率；

——导热率，W/(m·K)；

和ρ——混合气体和组分的密度，g/m3；

——斯蒂芬-玻尔兹曼常数，W/(m2·K4)；

p——多孔氧化层的曲折因子．

角标：

r——表示球形坐标系中某一位置；

s——表示颗粒表面、氧化层外表面；

b——表示氧化层内表面、反应界面；

∞ ——表示无穷远处．

［1］ 李 悦，胡春波，胡加明，等. 粉末火箭发动机研究进展[J]. 推进技术，2018，39(8)：1681-1695.

Li Yue，Hu Chunbo，Hu Jiaming，et al. Progress of powder rocket engine technology[J].，2018，39(8)：1681-1695(in Chinese).

［2］ Li Y，Hu C B，Deng Z，et al. Experimental study on multiple-pulse performance characteristics of ammonium perchlorate/aluminum powder rocket motor[J].，2017，133：455-466.

［3］ Szabo J，Miller T，Herr J，et al. Magnesium bipropellant rockets for martian ascent vehicles[C]//47San Diego，USA，2011：5834.

［4］ Huang H T，Zou M S，Guo X Y，et al. Analysis of the solid combustion products of a Mg-based fuel-rich propellant used for water ramjet engines[J].，2012，37(4)：407-412.

［5］ Huang H T，Zou M S，Guo X Y，et al. Analysis of the aluminum reaction efficiency in a hydro-reactive fuel propellant used for a water ramjet[J].，2013，49(5)：541-547.

［6］ Beach D B，Rondinone A J，Sumpter B G，et al. Solid-state combustion of metallic nanoparticles：New possibilities for an alternative energy carrier[J].，2007，129：29-32.

［7］ 王金云，王孟军，杨在林，等. 金属燃料技术研究进展[C]//第五届空天动力联合会议暨中国航天第三专业信息网第41届技术交流会论文集(第三册). 南京，2020：206-219.

Wang Jinyun，Wang Mengjun，Yang Zailin，et al. Re-search progress of metal fuel technology[C]//41st(3)Nanjing，2020：206-219(in Chinese).

［8］ Bergthorson J M，Goroshin S，Soo M J，et al. Direct combustion of recyclable metal fuels for zero-carbon heat and power[J].，2015，160：368-382.

［9］ Bergthorson J M. Recyclable metal fuels for clean and compact zero-carbon power[J].，2018，68：169-196.

［10］ Mandilas C，Karagiannakis G，Konstandopoulos A G，et al. Study of oxidation and combustion characteristics of iron nanoparticles under idealized and enginelike conditions[J].，2016，30(5)：4318-4330.

［11］ 刘世宁，胡春波，胡 旭，等. 基于产物分析的铁粉燃烧器燃烧特性实验研究[J]. 推进技术，2022，43(6)：385-396.

Liu Shining，Hu Chunbo，Hu Xu，et，al. Experimental study on combustion characteristics of iron powder burner based on product analysis[J].，2022，43(6)：385-396 (in Chinese).

［12］ 叶大伦，胡建华. 实用无机物热力学数据手册[M]. 第2版. 北京：冶金工业出版社，2002.

Ye Dalun，Hu Jianhua.[M]. 2nd Edition. Beijing：Metallurgical Industry Press，2002(in Chinese).

［13］ Wilson D B，Steinberg T A，Stoltzfus J M. Thermodynamics and kinetics of burning iron[J].，1997，1319：240-257.

［14］ 高文静，金 晶，曾武勇. 纳米铁粉的燃烧动力学模型研究[J]. 科学技术与工程，2013，13(33)：9808-9812.

Gao Wenjing，Jin Jing，Zeng Wuyong. Kinetic model study on combustion of nano iron powders[J].，2013，13(33)：9808-9812 (in Chinese).

［15］ 孙金华，卢 平，刘 义. 空气中悬浮金属微粒子的燃烧特性[J]. 南京理工大学学报，2005，29(5)：582-585.

Sun Jinhua，Lu Ping，Liu Yi. Combustion behavior of metal particles suspended in air[J].，2005，29(5)：582-585 (in Chinese).

［16］ Li S，Huang J Q，Weng W B，et al. Ignition and combustion behavior of single micron-sized iron particle in hot gas flow[J].，2022，241：112099.

［17］ Leshchevich V V，Penyazkov O G，Fedorov A V，et al. Conditions and delay time of ignition of iron microparticles in oxygen[J].，2012，85(1)：148-154.

［18］ 丁宋毅，孙 波，卓长飞. 基于粒子群算法的微纳米铁粉燃烧实验研究[J]. 科学技术与工程，2022，22(7)：2709-2716.

Ding Songyi，Sun Bo，Zhuo Changfei. Experimental research on combustion of micro/nano iron powder based on particle swarm algorithm[J].，2022，22(7)：2709-2716(in Chinese).

［19］ Schiemann M，Fischer P，Bergthorson J M. Iron particles as carbon-neutral fuel in spray roasting reactors[C]//8. Dubrovnik，Croatia，2017：487-492.

［20］ Mi X C，Fujinawa A，Bergthorson J M. A quantitative analysis of the ignition characteristics of fine iron particles[J].，2022，240：112011.

［21］ 肖兴国，谢蕴国. 冶金反应工程学基础[M]. 北京：冶金工业出版社，1997.

Xiao Xingguo，Xie Yunguo.[M]. Beijing：Metallurgy Industry Press，1997(in Chinese).

［22］ Gleeson B，Hadavi S M M，Young D J. Isothermal transformation behavior of thermally-grown wüstite[J].，2000，17(2)：311-318.

［23］ Juricic C. On the Mechanisms of Internal Stress Formation in Multi-phase Iron Oxide Scales[D]. Bochum：Ruhr University Bochum，2008.

［24］ Chen R Y，Yeun W Y D. Review of the high-temperature oxidation of iron and carbon steels in air or oxygen[J].，2003，59(5)：433-468.

［25］ Païdassi J. The kinetics of the air oxidation of iron in the range 700—1250℃[J].，1958，6(3)：184-194.

［26］ Neil B，Gerald H M，Frederick S P.[M]. 2nd EditionCambridge：Cambridge University Press，2006.

［27］ 李铁藩. 金属高温氧化和热腐蚀[M]. 北京：化学工业出版社，2003.

Li Tiefan.[M]. Beijing：Chemical Industry Press，2003(in Chinese).

［28］ Chen R Y，Yuen W Y D. A study of the scale structure of hot-rolled steel strip by simulated coiling and cooling[J].，2000，53(5)：539-560.

［29］ 李文超. 冶金与材料物理化学[M]. 北京：冶金工业出版社，2001.

Li Wenchao.[M]. Beijing：Metallurgical Industry Press，2001(in Chinese).

［30］ 葛庆仁. 气固反应动力学[M]. 北京：原子能出版社，1991.

Ge Qingren.[M]. Beijing：Atomic Energy Press，1991(in Chinese).

［31］ 李法社，王 华. 高等燃烧学[M]. 北京：科学出版社，2016.

Li Fashe，Wang Hua.[M]. Beijing：Science Press，2016(in Chinese).

［32］ Arshad U，Taqvi S A A，Buang A，et al. SVM，ANN，and PSF modelling approaches for prediction of iron dust minimum ignition temperature (MIT)based on the synergistic effect of dispersion pressure and concen-tration[J].，2021，152：375-390.

［33］ Liu Y X，Liu D，Liu G N. Energy conversion and ignition of iron nanoparticles by flash[J].，2017，60(12)：1878-1884.

［34］ Khaikin B I，Bloshenko V N，Merzhanov A G. On the ignition of metal particles[J].，1970，6(4)：412-422.

［35］ 杨 丽，朱燕群，王智化，等. 微纳米金属铁粉的燃烧特性试验研究[J]. 浙江大学学报(工学版)，2010，44(8)：1562-1566.

Yang Li，Zhu Yanqun，Wang Zhihua，et al. Experimental study of combustion characteristics of micron and nano iron powders[J].()，2010，44(8)：1562-1566 (in Chinese).

Heterogeneous Ignition Model and Ignition Characteristics of Iron Particle

Cai Ping，Xu Yihua，Hu Kun，Chen Xuanren，Yang Zhihao，Sun Haijun，Ren Guanlong

(Jiangxi Key Laboratory of Micro Aeroengine，School of Aircraft Engineering，Nanchang Hangkong University，Nanchang 330063，China)

The heterogeneous ignition model of iron particles in air was established based on shrinking unreacted-core model，taking into account the influence of oxygen diffusion in the oxide layer on the ignition process. The maximum error between the calculated ignition temperature by this model and the experimental ignition temperature is 6.95%. Compared with Mi's ignition model，the particle heating rates calculated by the two models are basically the same，and their ignition delay time is of the same order of magnitude. The influences of atmospheric pressure，oxygen concentration，initial oxide-layer thickness and particle diameter on ignition temperature and ignition delay were studied based on this model. The results showed that ignition temperature and ignition delay decrease with the increase of atmospheric pressure and oxygen concentration but increase with the increase of initial oxide-layer thickness. The ignition temperature within the range of particle diameter less than 10μm increases with the decrease of particle diameter，and within the range of 10μm to 50μm，it is hardly affected by particle diameter. The ignition delay time increases as the particle diameter increases.

iron particle；fuel；heterogeneous ignition model；ignition temperature；ignition delay

TK16

A

1006-8740(2024)01-0091-12

2023-03-01．

国家自然科学基金资助项目(51666012；12102161)；航空科学基金资助项目(20200001056001).

蔡 平(1998— )，男，硕士研究生，caipinghead@163.com.

徐义华，男，博士，教授，xuyihua@nchu.edu.cn.

(责任编辑：隋韶颖)