重力三维密度光滑反演软件设计与实现
彭衍武 陈文进 谭小龙 洪国庆
1 江西理工大学土木与测绘工程学院,江西省赣州市客家大道1958号,341000
通过重力密度反演分析技术可以更准确地了解地质体结构、形状及其他特征,为此,国内外学者进行大量工作。Li等[1-2]引入深度加权函数;Portniaguine等[3]引入最小梯度支撑函数约束重力反演;Chasseriau等[4]提出基于随机方法的反演技术;Zhdanov[5]提出重磁反演和成像新方法;Commer[6]提出深度分辨率增强的加权方案;耿美霞等[7]建立在密度约束下的多变量协同克里金联合反演方程;张志厚等[8]提出一种基于深度学习的重力异常及重力梯度异常的联合反演方法。
在三维密度反演领域已经存在诸多算法,但可用于密度反演的公开软件却很少。基于此,本文借助 MATLAB语言,开发一个支持三维密度反演、重力场正演、数据分析及可视化等功能的系统软件,为重力三维密度反演学习和研究提供软件工具支持。
1 方法原理
1.1 重力场正演
根据牛顿万有引力定律,由计算点体积质量密度元素产生的万有引力势为[9]:
(1)
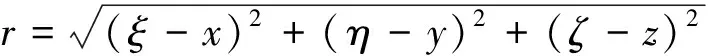
(2)
式中,r为径向矢量;ΔVj为第j个棱柱体的体积;ρj为第j个棱柱体的密度;M为长方体总数。本文采用Nagy等[10]推导的位、引力矢量和引力梯度张量表达式用于重力场正演计算。
1.2 三维密度反演
根据待求解密度模型的特点建立合适的反演目标函数:
S=φd+μφm
(3)
式中,φd为数据拟合项。通常认为重力数据观测噪声符合高斯分布特点,因而采用L2范数进行构建:
(4)
式中,Wd为每个数据点的权重方阵;dobs为观测数据点的N×1维向量;dpre为预测数据点的N×1维向量。模型拟合项定义如下:
(5)
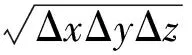
(6)
式中,z0为观测高度;z为单元深度;β为拟合指数项。因此,目标函数可表示为:
φ(ρ)=φ(ρ)d+μφm(ρ)
(7)
最后,通过最小二乘可得:
(8)
2 软件设计与功能
本文软件是基于 Windows10系统,开发环境为Intel(R) Core(TM) i5-9300H CPU,8G内存。系统结构和操作流程如图1所示。该软件由三维密度反演和数据结果界面两部分组成(图2),主要功能包括参数设置、地下模型空间划分、重力观测数据选择、反演结果显示与预测。
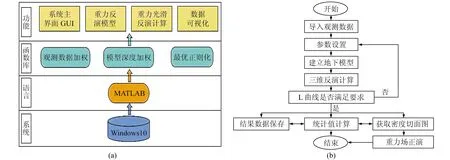
图1 系统设计框架与操作流程
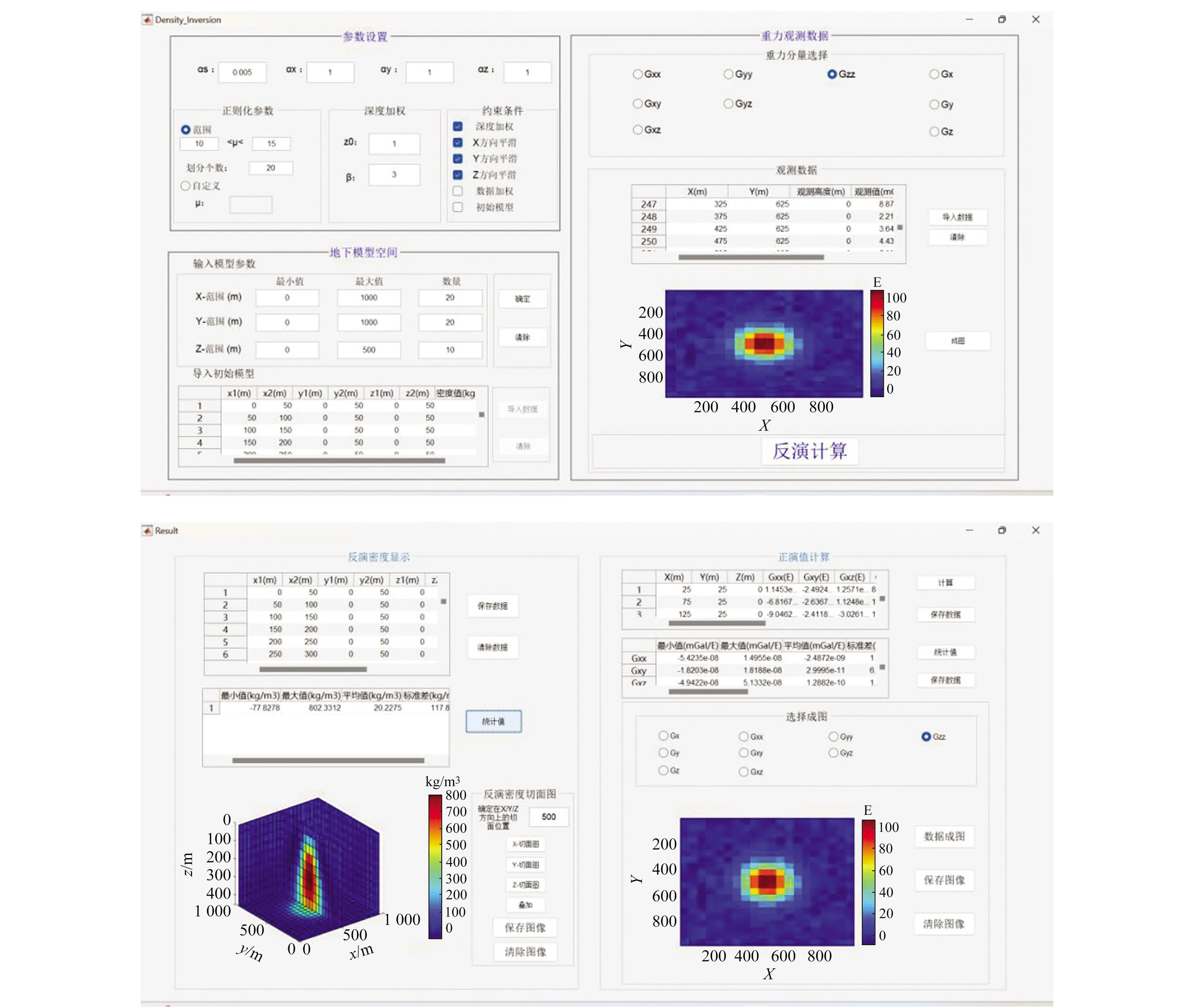
图2 三维密度反演主界面与子界面
3 数据测试
3.1 单长方体模型数据测试
测区范围为1 000 m×1 000 m×500 m,网格划分为20×20×10,单模型x轴范围为400~600 m,y轴范围为400~600 m,z轴范围为100~300 m,密度为1 g/cm3。模型切面及观测数据如图3所示,反演结果如图4所示。

图3 模型切面与重力观测数据
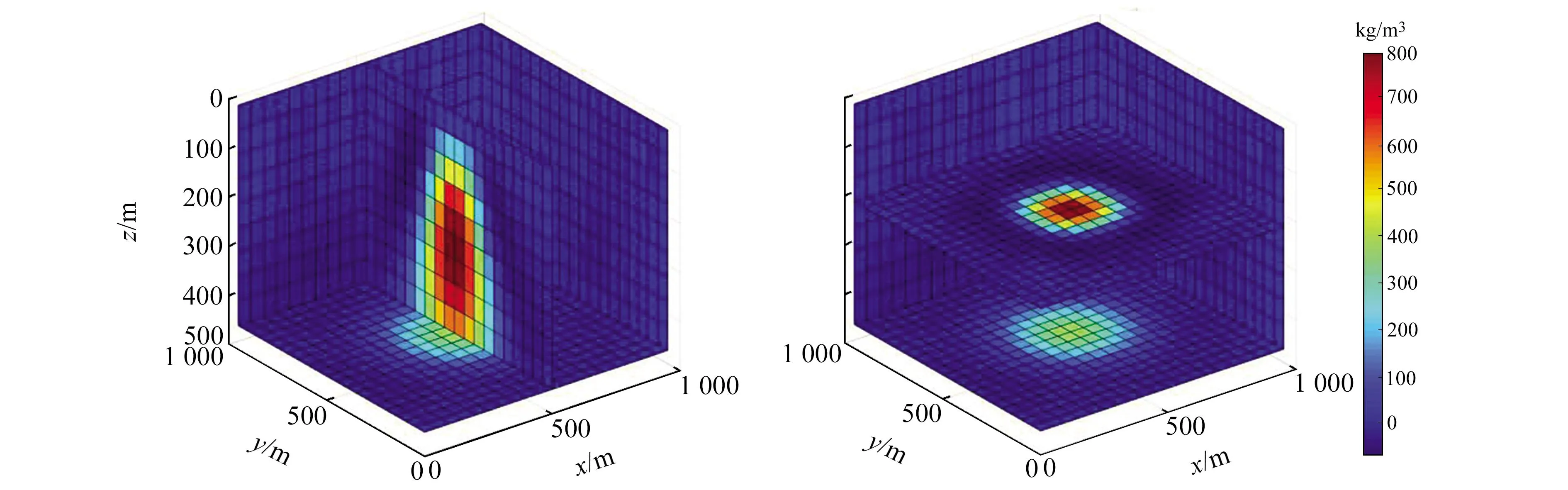
图4 反演模型在x=500 m、z=200 m处密度切面
从图4可以看出,反演结果能够有效地反映地质体的空间分布,验证了本文软件的有效性。
3.2 实测数据测试
本文采用文顿盐丘(Vinton Dome)地区重力梯度实测数据进行反演测试。文顿盐丘位于美国墨西哥湾沿岸,该地区岩盖密度约为2.75 g/cm3,盐丘附近沉积物、围岩及盐核密度均约为2.2 g/cm3,即岩盖剩余密度约为0.55 g/cm3。本文选用的测区范围为4 000 m×4 000 m×1 000 m,网格划分为40×40×20。
图5为实测重力梯度gzz和预测gzz数据,由图可知,预测数据与实测数据拟合效果较好。图6为密度反演结果,从图中可以看出,反演密度集中部分顶部埋深约为200 m,底部埋深约为600 m。该结果与前人研究所得埋深结果200~650 m[11]、200~550 m[12]较为接近,验证了软件的可靠性与实用性。

图5 实测重力梯度数据与密度异常体预测数据

图6 反演模型在y=2 000 m、z=300 m和z=700 m处密度切面
4 结 语
本文开发出一个重力三维密度光滑反演软件,具有最优正则化参数选取、数据文件管理、密度反演计算及结果分析和可视化等功能。模拟和实测数据测试结果验证了该软件的有效性与实用性,未来可以在计算效率等方面进一步优化。

