基于BO-WT-VMD 组合模型的钢丝绳的损伤信号降噪方法

朱宇坤，黎 恒，吴文俊，柯圆圆*

（江汉大学 a.智能制造学院，b.人工智能学院，湖北 武汉 430056）

0 引言

在日常生产生活中提升机随处可见，如矿井提升机、多功能提升机、缠绕式提升机、摩擦式提升机、井塔式提升机、多绳摩擦式提升机等。提升机的工作原理是通过动力机械拖动钢丝绳及所运输的货物进行上下运动以完成运输过程。钢丝绳是提升机不可或缺的重要组成部分，在运行过程中钢丝绳会出现老化、磨损和结构断丝等现象，对安全生产造成影响。如何在不损害钢丝绳性能和不影响钢丝绳使用的前提下，通过信号建立一个有效的钢丝绳故障监测模型显得很有必要。例如，文献［1］对钢丝绳损伤识别方法进行了研究。

要实现钢丝绳故障的识别，需消除或者减少噪音对原始信号造成的影响，同时需要保留原始的有效信息，因此需要对采集的信号进行降噪处理。信号降噪的传统方式是进行频谱研究。因噪音信号一般处于高频部分，有效信号频谱主要分布于低频区域，故可对原始信号进行傅里叶变换［2］，保留低频区域的信号以完成信号去噪。但实际上，钢丝绳检测信号往往是不规律的，含有离群点和突变的可能性很大。使用传统的降噪方式不能有效地分离由噪声引起的高频信号和中频信号，且会使中频信号缺失，致使对钢丝绳损伤状况有用的检测信号丢失，从而影响检测结果。

1986 年，数学家Meyer 和Mallat 建立了构造小波基的统一方法——多尺度分析。此后，学者们提出了利用小波变换［3-6］对信号进行去噪，如朱金玲［6］针对ECG 信号，利用小波变换有效地消除了ECG 信号中的噪声影响，并保持了与原始信号之间的一致性。通常，小波变换在高斯白噪声的处理过程中效果尤为显著。如何选取小波基和分解层数是信号处理问题的关键，而噪音信号是无法完成自适应降噪的。经验模态分解（empirical mode decomposition，EMD）算法是一种将复杂信号分解为一组平稳化的数据序列集，以原始数据为“基”的自适应数据处理方法。它在处理非平稳及非线性数据上有着明显优势［7-10］。王晓蓉等［10］针对铡草机振动信号采用EMD 去噪，使得信噪比得到了提高。因EMD 在运算时容易出现端点效应和模态分量混叠现象，而变分模态分解算法（variational mode decomposition，VMD）［11-13］通过迭代搜索变分模型最优解的方式，将非平稳混合信号分解为多个单分量模态，通过控制带宽来避免混叠现象，是一种自适应、完全非递归的模态变分模型和处理方法，广泛应用于非平稳信号的去噪。VMD 分解的效果会受参数惩罚因子α和模态分解个数K值影响，选取不当会造成信号过分解或分解不完全，影响降噪结果［14-15］。

本文以某六绳提升机的钢丝绳信号数据为样本，提出了基于贝叶斯优化-小波变换-变分模态分解（BO-WT-VMD）组合的信号降噪模型。首先利用小波变换确定小波层数并对原始信号进行去噪，然后利用VMD 算法进行二次降噪。再采用贝叶斯优化算法［16］进行寻参，获取最优的α和K的超参数组合，再将所得参数α和K的值代入VMD 算法中，得到分解后的K个模态。通过皮尔逊系数选择最优的模态，剔除剩余模态，最终得到去噪后的重构数据，为钢丝绳故障监测模型的建立提供了良好的基础。在仿真实验和真实数据中，分别计算了BO-WT-VMD、WT 和VMD 算法的SNR值和RMSE值。最后，为了找出去噪信号故障的程度、位置和数量，采取局部离群因子检测技术（local outlier factor，LOF）计算每点在相应区间的局部离群因子，从而确认故障点的位置、数目和程度。

1 基于BO-WT-VMD的组合降噪模型

1.1 小波变换

小波分析法是一种窗口大小固定，时宽和频宽可变的时频局部化分析方法，利用基本小波函数替代Fourier 变换中的基函数，与待分析信号作内积。假设f(x)是平方可积函数，将f(x)的小波变换定义为

式中，a和b分别是尺度因子和时移因子；φa,b(x)是小波基函数。

因钢丝绳检测信号为一维离散信号，故在数值计算中需要将小波变换的尺度因子和时移因子分开。设比例因子a=,b=0，其中a0＞1,b≠0，m与n均为整数。小波基函数为

当h,a0,b0取合适值时，hm,n(x)构成标准正交基。阈值公式利用软硬阈值折中的方法，具体为

式中，cD1为第一层分解的细节系数；N为数据长度。

同时，小波变换采用如下的阈值函数进行变换：

式中，当a=0 时，该函数为硬阈值函数；当a=1 时，该函数为软阈值函数。因本文采取软硬阈值折中的方法，故a取值0.5。

为了有效地过滤钢丝绳的损伤干扰信号，提升钢丝绳的在线检测效果，本文设计了钢丝绳损伤信号的小波变换预处理模型，具体流程如图1 所示。图1 中f(iΔs)表示通过距离采样的输入信号；M表示形态滤波器；Y（0），Y（1），…，Y（n）表示由形态滤波器处理的信号；H（i）和L（i）分别表示经过第i层小波变换后故障信号的详细高频信息和一般低频信息。根据图1 的流程图，钢丝绳损伤信号的预处理模型在小波变换的每一层中都有一个附加的形态学滤波器。利用此形态滤波器，可去除操作过程中由于钢丝绳摇晃而产生的一维钢丝绳损伤信号的漂移信号。然后，利用小波变换方法作进一步分析，具体步骤如下：

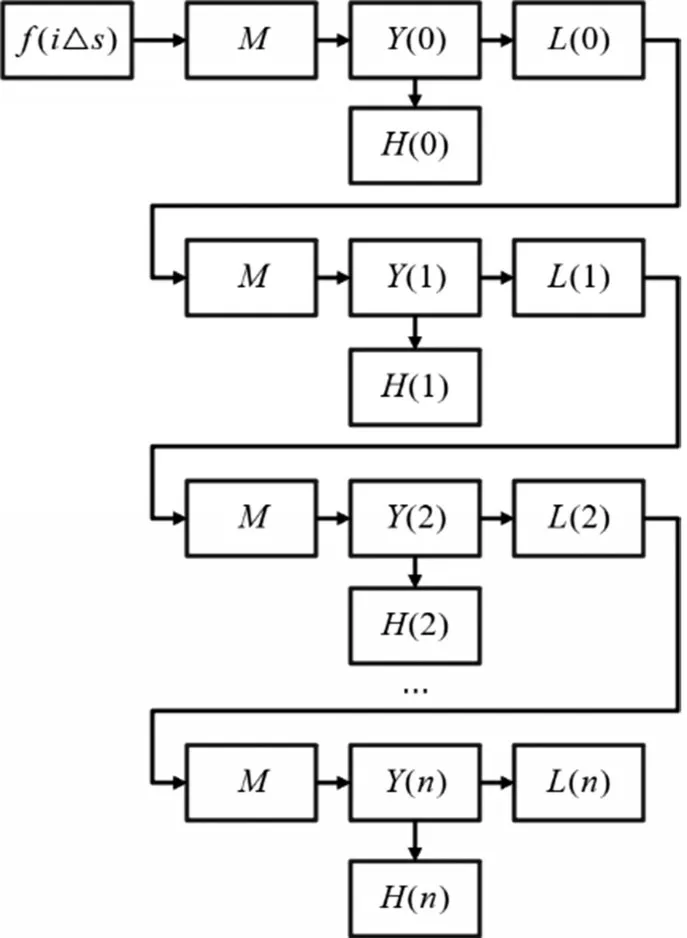
图1 小波变换具体流程图Fig.1 The flow chart of the wavelet transform

步骤1：对噪音信号进行小波分解。选择对应的分解尺度与小波基，进行小波分解，得到一组小波系数。

步骤2：对小波分解的各层高频系数进行阈值量化，从而得出小波系数的估计值。

步骤3：将已经阈值量化后的小波系数值进行逆小波变换以重构信号，从而得到去噪后的信号。

1.2 VMD 算法

VMD 是对变分问题的一种求解过程，该算法所进行的自适应信号分解过程是通过求解寻找约束变化模型的最优解来实现的。在该算法模型中，将输入信号x(t)根据预设的分解尺度K以及二次惩罚因子α被分解成K个稀疏模式的IMF 分量，用uk(t)表示。每个IMF 分量都有一个中心频率的有限带宽，中心频率和带宽在分解过程中将会不断更新。每个IMF 分量又被定义为调幅调频信号，即

其中Ak(t)是uk(t)的瞬时赋值，ϕk(t)为其相位函数，其瞬时相位ωk(t)=ϕk(t)。

利用交替方向乘子表，计算增广拉格朗日函数的鞍点，得到最优解{uk},{ωk}和λk。将原始信号f分解为K个IMF 分量，具体步骤如下：

1）设n=0，初始化{uk1},{ωk1}和λ1，其中n为迭代次数。

2）当n=1，循环开始，并更新{uk},{ωk}和λk。

（a）当ω≥0 时，迭代更新{uk}的值，具体数学表达式为

（b）迭代更新{wk}的值，具体迭代为

（c）当IMF 分量及其中心频率被更新时，拉格朗日乘数λ也被更新为

3）设n=n+1，重复迭代更新uk,wk，直至满足收敛条件

式中，ε为预先给定的判别阈值。当满足约束条件时，则可停止迭代并输出K个模态分量。

1.3 确定最佳模态分量

利用图1 所示的降噪流程对采集到的声波信号，利用小波包分析进行降噪处理，确定小波包分解层数，小波基函数及阈值函数，得到初步处理后的去噪信号；再对这些信号进行VMD 分解，得到K个IMF 分量，并利用相关系数公式计算各IMF 分量间的相关系数，选取阈值满足条件ρ＞Cmax/(10Cmax-3)的IMF 分量为有效的IMF 分量，其中Cmax为各分量与原始信号的最大相关值；最后，将提取的有效的IMF 分量进行信号重构，得到去噪后的重构信号。

相关系数是指两个变量之间的相关程度，相关系数的绝对值越大，说明相关性越强，相关系数越接近于0，相关性越弱，具体公式为

式中，Cov(xi,yi)和σx,σy分别为xi和yi的协方差和标准差。本文用去噪后信号与原始信号之间的相关系数表示去噪效果，相关系数C越趋于1，说明去噪效果越好。

1.4 贝叶斯优化算法

贝叶斯优化算法（Bayesian optimization，BO）［16］是指在目标函数未知的情况下，利用贝叶斯定理来指导搜索找到目标函数最大值或最小值的方法，也就是通过代理优化的方式找到全局最优解。它有效地解决了序贯决策理论中经典的机器智能问题，能通过较主动选择相对好的策略来确定下一个最有“潜力”的评估。在贝叶斯优化算法中，其核心问题是构建代理函数和采集函数，常用的代理函数是高斯过程，它能建立与目标函数近似的模型，并能获取下一个评估的位置，在某些场景下，合理选用高斯过程可以有效改进贝叶斯优化结果。

设待优化模型的超参数集合为X={x1,x2,…,xn}，贝叶斯优化算法的目标函数为f(x)，则贝叶斯优化算法遵循如下的二项分布：

式中，GP为高斯分布，μ为均值，k(x,x')为协方差函数。

利用贝叶斯优化算法，经过t次迭代试验后可得到数据(xt,f(xt))，此时有数据集Dt={(x1,f(x1)),(x2,f(x2),…,(xt,f(xt)))}。然后，我们便需要预测集合第t+1 处的数据(xt+1,f(xt+1))。将第t+1 处的点分布在某个t+1 维度的高斯分布中，也就是：

式中，K为协方差函数矩阵，k=[(xt+1,x1),(xt+1,x2),…,(xt+1,xt)]，由此可以得出ft+1的分布，即

式中，μ(xt+1)=kK-1f1:t，它表示预测均值；δ2(xt+1)为预测协方差，其值为k(xt+1,xt+1)-kK-1fT。由此可得集合t+1 处的数据(xt+1,f(xt+1))。

贝叶斯优化算法以伪代码形式的执行流程如下：

综上，本文使用BO 来改进VMD 算法，利用基于BO-WT-VMD 的组合降噪模型对原始信号进行去噪处理，其大致过程如下：

首先，利用小波变换确定小波层数，并对原始信号进行去噪。其次，利用贝叶斯优化确定VMD 的参数K与α，即：首先随机初始化超参数组合与先验数据集，通过高斯模型GP 增加采样点，得到后验数据集，若后验数据集满足终止条件，则确定优化后的参数组合，得到小波变换的参数；若后验数据集不满足终止条件，则通过循环高斯模型及前面的步骤，直至后验数据集满足终止条件，确定优化后的参数组合，得到VMD 的参数K与α。最后，将所得参数K与α的值代入VMD 算法中，得到分解后的K个模态，然后通过皮尔逊系数选择最优的模态，剔除剩余模态，最终得到去噪后的重构数据，具体模型框架如图2 所示。

图2 BO-WT-VMD 模型框架图Fig.2 The framework of the BO-WT-VMD model

2 降噪效果评价

一般地，降噪效果采用主观评价法和客观评价法。主观评价法会受人为因素的影响，具有一定的主观性。客观评价法是建立在质量指标体系基础上，通过不同的指标来判定降噪效果的方法。本文采取信噪比和均方根误差来评价信号的降噪效果。

1）信噪比（SNR）：指有用信号功率与噪声信号功率的比值，即

式中，x(i)为原始信号；(i)为降噪后的信号；N为信号长度。信噪比SNR越大，表示降噪效果越好。

2）均方根误差（RMSE）：指观测值与真实信号偏差的平方和，与观测次数N之比值的平方根，即

均方根RMSE误差越小，表示降噪效果越好。

3 基于BO-WT-VMD 算法的仿真实验

为了对本文提出的BO-WT-VMD 降噪方法进行可行性分析，先对仿真信号进行降噪分析，设仿真信号表达式为

式中，信号频率为2、24、288。观测信号由不同分贝的高斯白噪声和有线信号叠加而成。评价的参数指标采用信噪比（SNR）和均方误差（RMSE）。

为比较不同算法的降噪效果，本文分别对VMD、WT 和BO-WT-VMD 算法利用仿真信号进行降噪，得到的3 种算法降噪性能结果如表1 所示。

表1 3 种算法降噪性能表Tab.1 Noise reduction performance of 3 algorithms

由表1 可知，在3 种降噪算法中，BO-WT-VMD 算法的SNR值最大，为17.340 3，RMSE值最小，为0.101 0，说明BO-WT-VMD 模型对噪声数据的降噪性能最好。

仿真函数值的降噪效果如图3 所示。分析图3 可知，WT 算法无法完整返回仿真函数的有效信息；VMD 算法在某些极值点处无法很好地拟合；相比之下，BO-WT-VMD 算法很好地弥补了以上算法的不足，对仿真函数值的降噪效果良好，因此BO-WT-VMD 算法具有良好的降噪效果。BO-WT-VMD 模型对信号的模态分解结果如图4 所示。图4 显示了对原函数图像利用BO-WT-VMD 模型得到的3 个IMF 分量，而IMF3为噪音分量是需要去掉的。

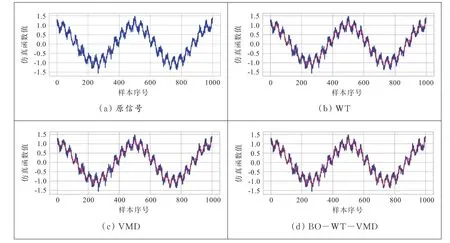
图3 仿真函数值的降噪前后对比图Fig.3 Comparison diagram of simulation function values before and after denoising

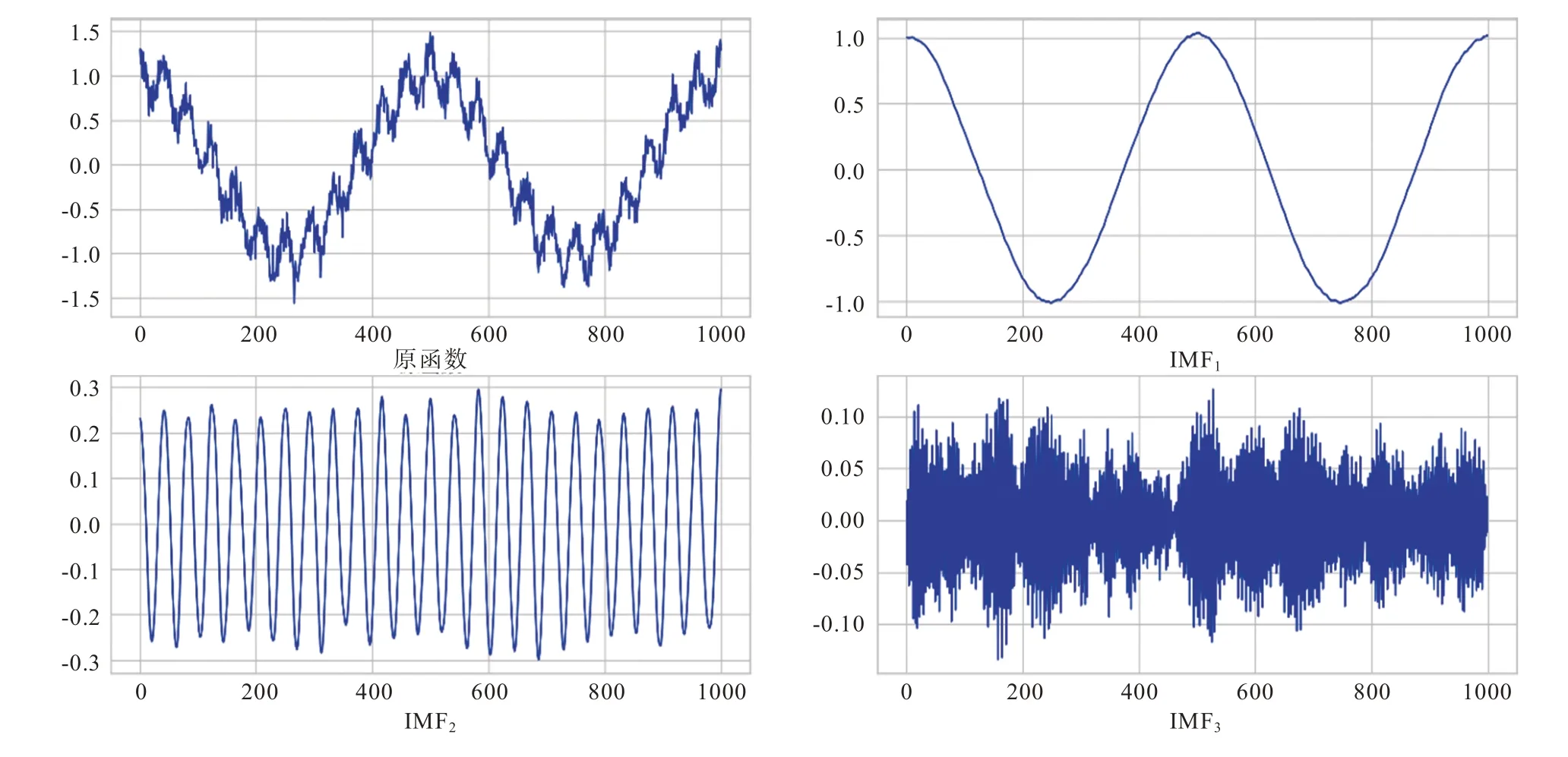
图4 模态分解结果图Fig.4 Result diagram of modal decomposition

4 六绳提升机的信号去噪实验数据分析

为检验BO-WT-VMD 算法真实数据的降噪结果，本文选取文献［17］提供的数据进行检验。该数据是假设在六绳提升机中，六根长度为960 m 的钢丝绳在井筒中升降往返10 次的监测数据。因有六根钢丝绳，故与之对应的共有六组电压数据，分别命名为1 号电压到6 号电压。不失一般性，本文分别从1 号电压和2 号电压中抽取样本序号为5 000～6 000 的电压，使用BOWT-VMD 算法对其进行降噪预处理，并分析其降噪效果，降噪前后对比图如图5 和图6 所示。

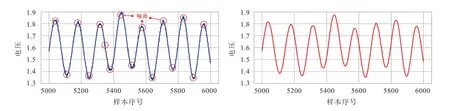
图5 1 号电压降噪前后对比图Fig.5 Comparison of voltage 1 before and after denoising

图6 2 号电压降噪前后对比图Fig.6 Comparison of voltage 2 before and after denoising

通过分析图5 和图6 可知，BO-WT-VMD 算法对文献［17］中的题目所给信号数据具有较好的降噪效果，能够准确地剔除噪音部分，完成信号去噪。因此，BO-WT-VMD 算法对于噪音数据，特别是钢丝绳断丝损伤信号有着良好的降噪效果，可对后续损伤信号特征量进行准确提取，从而提高钢丝绳断丝损伤信号定量识别的准确度。

为了监测降噪信号的故障数目、位置和程度，采取局部离群因子（LOF）算法对降噪信号进行分析，通过判断每个点输出的局部离群因子找出故障信号点并统计，利用文献［17］所给的量化定义公式计算出损伤程度与位置。

LOF 算法是一种典型的基于密度的高精度离群检测方法，通过给每个数据点都分配一个依赖于领域密度的离群因子LOF，进而判定该数据点是否为离群点。若异常分数LOF值接近1，表明样本点P与其邻域对象密度越接近，越有可能与邻域同属一簇；若异常分数LOF值小于1，表明样本点P处于一个相对密集的区域，不像一个异常点；若异常分数LOF值远大于1，表明样本点P与其他点比较疏远，很可能是一个异常点。

下面对算法中的相关概念，如对象的第k距离（设k为正整数）、k距离邻域、数据对象的可达距离、可达密度和局部离群因子描述如下：

1）数据对象P的第k距离：是指距点P最近的第k个点的距离，记为dk（P）。设两个数据对象P与Q的距离为d（P，Q），且满足如下条件：

A.数据集D中至少存在不包括点P的k个点Q'∈D{P}，使得d(P,Q')≤d(P,Q)；

B.数据集D中至多存在不包括点P在内的k-1 个点Q'∈D{P}，使得d(P,Q')＜d(P,Q)。则dk（P）=d（P，Q）是数据对象P的第k距离。

2）对象P的第k距离邻域：指所有与点P的距离小于等于dk（P）的数据对象Q'的集合Nk（P），即

3）可达距离：数据对象P与Q的可达距离记为reach-distk（P，Q），它至少是点P的第k距离dk（P），即

事实上，距离P点最近的k个点，它们到P点的可达距离被认为是相当的，且都等于dk（P）。

4）局部可达密度：数据对象P的局部可达密度是指点P的第k邻域内所有到点P的平均可达距离的倒数，即

5）局部离群因子：数据对象P的局部离群因子是指点P的邻域Nk（P）内其他点的局部可达密度与点P的局部可达密度之比的平均数，即

通过LOF 算法得到可能的异常点，并分析2 号电压的第248 000～250 000 和第240 400～242 400 个信号数据的电压变化趋势与局部异常因子的变化趋势（分别记为变化趋势（a）和变化趋势（b））来判断算法的可靠性，其中变化趋势如图7 和图8 所示。

图7 电压与局部异常因子变化趋势（a）Fig.7 Trend of voltage and local anomaly factor（a）

图8 电压与局部异常因子变化趋势（b）Fig.8 Trend of voltage and local anomaly factor（b）

通过对图7 和图8 的分析可知，电压发生突变的点在对应的局部异常因子上也有明显的突变，而且所对应的位置基本一致，故该算法具有良好的检测到异常因子的能力。通过LOF 算法的监测，得到了6 根钢丝绳在往返运行10 次后的异常因子数，各钢丝绳的缺陷数量如图9 所示。

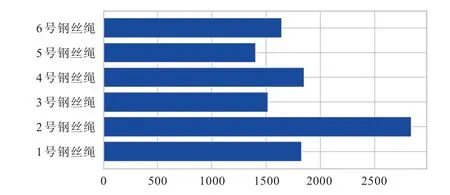
图9 各钢丝绳的缺陷数量图Fig.9 The defect number of each wire rope

各钢丝绳不同程度的缺陷数量以及缺陷对应位置如表2、表3 所示。

表2 各钢丝绳不同程度缺陷数量Tab.2 The quantity table of different degree defects of each wire rope

表3 各钢丝绳缺陷所在位置Tab.3 The defect location of each wire rope

5 结论

本文针对VMD 中参数K需要人为设定的问题，使用了一种基于贝叶斯优化集成软硬阈值折中变分模态分解的方法，实现了对仿真信号数据和钢丝绳断丝损伤信号数据的降噪处理，通过分析和实验验证得出了以下结论。

1）运用贝叶斯优化算法优化变分模态分解的超参数K和α，有效地解决了传统变分模态分解算法中K和α需要人为设定的问题，实现了信号最优分解，有效地避免了信号分解不足或者过分解。

2）在仿真信号中，与变分模态分解降噪法、小波包阈值降噪法相比，基于贝叶斯优化集成软硬阈值折中变分模态分解的降噪方法的SNR值较大，RMSE值较小，降噪效果更好。

3）在实际工程中采集到的原始含噪信号，经过贝叶斯优化集成软硬阈值折中变分模态分解的降噪方法降噪后，可以在消除噪声的同时有效地保留信号，可对后续损伤信号特征量进行准确提取，从而提高钢丝绳断丝损伤信号定量识别的准确度。

本文所采用的BO-WT-VMD 算法对于噪音数据有着良好的降噪效果，但相比传统降噪方法用时较长，不利于处理大数据的降噪，后期可从结合机理的角度和综合使用人工智能方法进行数学建模来研究解决大数据降噪的问题。