基于PCA 和ICA 模式融合的非高斯特征检测识别

葛泉波 程惠茹 张明川 郑瑞娟 朱军龙 吴庆涛

在复杂水域中,无人船(Unmanned surface vehicle,USV)需要准确地了解自身的位置、姿态和运动状态,以便进行自主导航和避障.位姿测量是无人船实现自主导航和避障的关键技术之一.位姿测量可以通过多种传感器来实现,如GPS、惯性测量单元、视觉传感器等.这些传感器可以提供无人船的位置、速度、加速度、角速度等信息.在无人机-无人船协同降落场景中,无人船需要面对各种复杂的环境 (风浪流),这些环境会对无人船的运动状态以及后续无人机相对位姿的准确估计产生影响,因此需要准确的位姿测量来保证无人船的安全和稳定性.

在位姿估计或目标跟踪状态估计算法中,通常使用的是基于卡尔曼滤波的方法,文献[1]中基于EKF 给出了三种典型非线性集中式融合算法,并在非线性系统中推广与完善;Fu 等[2]提出了一种基于动态递归标称协方差估计和改进变分贝叶斯推理的增强自适应卡尔曼滤波;Gao 等[3]提出了一种基于马氏距离的自适应加权联邦卡尔曼滤波方法,提高了导航滤波计算的精度;文献[4]中提出一种复合自适应滤波算法,解决了一类过程噪声统计特性未知且系统状态分量可观测度差的状态估计问题.在卡尔曼滤波中,存在过程噪声和测量噪声两个噪声源.如果过程噪声和测量噪声都服从高斯分布,那么卡尔曼滤波器能够提供一个最优的线性无偏估计;如果噪声是非高斯的,那么卡尔曼滤波器可能无法准确地描述数据的真实分布,从而导致估计误差的增大.因此,对这些不确定噪声的高斯性和非高斯性进行判别是后续建模的关键,而随机噪声变量的非高斯性/高斯性判别主要依赖于随机变量概率分布曲线的峰度与偏度系数的检验,因此,对峰度与偏度系数的高性能估计成为关键.

近些年,有许多学者对基于峰度和偏度的非高斯判别方法进行研究[5-8],Mardia[5]基于偏度和峰度建立了多维正态性检验统计量.此后,许多学者对这一类型的检验进行了研究,使其理论不断丰富和发展.Srivastava[6]对偏度和峰度在多维情形下做出了不同的推广,提出了自己的多维正态性检验统计量;文献[6]中所提到的多维正态性检验方法,对于高维和大样本情形,可以考虑T 型多维峰度作为正态性检验统计量,许多国内学者也针对多维数据降维技术进行了研究和实验[9-12].孙平安和王备战[13]验证了主成分分析(Principal component analysis,PCA) 存在会损失部分有用信息并且容易受到噪声影响的缺陷;Zhou 等[14]对基于PCA 和CCA 的特征降维算法进行了有效的研究.Sharma 和Saroha[15]将PCA 方法与特征排序相结合,最终验证将PCA 与特征排序相结合的方式可以在提升分类精度的基础上实现降维.刘文博等[16]提出一种基于加权核主成分分析的维度约简算法,证明随着数据维度的增加,多核学习的优势更明显.如何构造更加多样化的核函数以提高数据处理效率成为了研究重点.

本文在现有技术的基础上,提出了一种基于PCA 和独立成分分析 (Independent component analysis,ICA)模式融合的非高斯特征检测识别方法,以期得到更优的检测效果.

1) 提出一种基于标准化加权平均和信息熵的数据预处理方法.首先采用标准化加权平均对数据进行规范化处理,然后通过计算信息熵和信息偏差度来消除一些数据的不确定性.

2) 提出一种基于混合加权核函数的主成分分析方法.该方法使用加权核函数对PCA 进行改进,旨在对高维数据特征进行维度约简,降低数据的复杂度,从而实现简便的数据降维,同时提出一种改进的灰狼优化(Grey wolf optimization,GWO)算法来优化参数.

3) 提出一种基于ICA 和PCA 联合的相关性分析方法进行数据降维.该方法使用改进的PCA 算法对数据进行降维,将降维后的数据与经过ICA 处理的数据进行相关性分析,以确定最终的降维成分.

4) 在降维数据的基础上综合T 型多维偏度峰度检验方法和KS (Kolmogorov-Smirnov)检验方法进行检测识别,对数据进行多元正态分布拟合并且考虑到样本容量和样本分布状况.

1 系统描述

1.1 传统PCA 的问题分析

PCA 是一种数据分析技术,它可以高效地找出数据中的主要部分,将原有的数据降维并去除整个数据中的噪声和冗余.

1) 传统利用PCA 进行降维处理的方法用零均值化对数据进行特征缩放.简单的均值相减并不能达到数据预处理的目的,因此需要考虑对数据预处理过程进行改进和完善,以保障后续的计算结果.

2) PCA 只能解决数据分布是线性的情况.实际工程系统中,需要考虑到非线性噪声的处理.文献[17]中通过使用核主成分分析把非线性的数据映射到高维空间实现线性模式转化,然后用PCA来进行降维处理[18],但其计算相对复杂,需考虑提高其处理效率.

3) PCA 整个计算过程就是通过一个协方差矩阵的特征值分解来起到降维效果的.PCA 降维是选取方差最大的主成分,难免会损失一些信息[19],因此,研究过程中需要考虑的是如何有效降维并且获得精确的降维结果.

1.2 研究动机

本文主要研究基于PCA 降维的非高斯特征判别在多维数据中的应用.PCA 在数据特征提取方面具有一定优势,但在多维数据降维处理过程中,仍存在以下几个问题:

1) 零均值化处理得到的数据难以很好地全面表征原始数据的综合特征[20].由于均值容易受到极端值的影响,所以在对数据完全无知的情况下,简单的均值处理并不能较好地保留数据特征信息.

2) 现有非高斯检测方法中,基于PCA 的协方差矩阵求解技术难以保证协方差矩阵不受非线性噪声的影响,从而将严重影响最终的降维效果[21-23].在实际应用中,采用主成分降维后进行正态检验可能会受到非线性噪声影响,从而极易影响检验效果.

3) 非高斯数据求解得到的特征值和特征向量不一定是最优解,难以很好地表达原始数据的基本特征[24-25].PCA 主要通过寻找数据矩阵的特征值和特征向量,然后使用坐标旋转得到主成分,所以如果输入数据不是高斯分布,特征值和特征向量就不能代表数据的特征,这样PCA 也就失去了它的意义[26].

1.3 解决方案

面对上述多维数据PCA 降维中存在的问题,针对性地提出以下解决方案,改进后方案的具体过程如图1 所示.

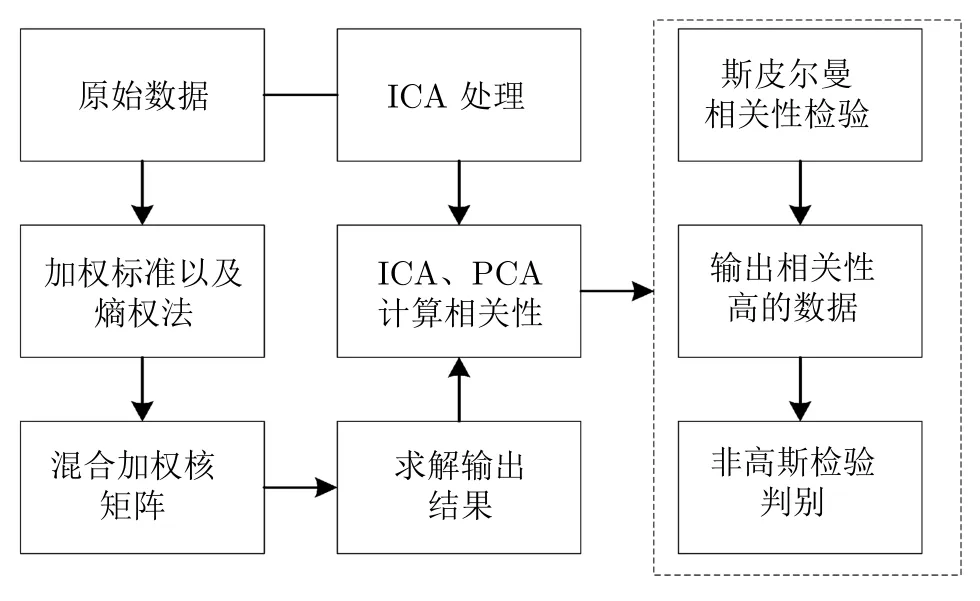
图1 主成分分析改进方案过程Fig.1 Principal component analysis improvement plan process

2 基于信息熵的混合加权核主成分分析

2.1 改进的数据预处理过程

在对数据完全无知的情况下,本文通过对原始数据集采用特征加权平均值进行改进,保留了特征间差异性,使降维后保留的信息量也更具有价值,此外,为了提高数据预处理的可靠性,本文使用熵权法进行数据筛选,筛除对结果贡献率较低的数据.

2.1.1 加权平均的数据处理过程

将原始数据按列组成n行m列矩阵X(n×m),以当前值减去数据集中该特征的加权平均值Dx,Dx的计算如式 (2) 所示,其中的权重分配方式参考每个特征算出的均方差σd,加权平均处理后得到矩阵具体计算公式如下所示

式 (2) 为数据平均值和加权平均值,式(3)为得到的数据预处理结果,xi为每行各个元素,为对应的均值,Dd为每行各个元素与均值之差,每行均值之差构造矩阵D(n×m),ω d为每个元素对应σd所分配的权重值并且ω d之和为1,其中ωd利用均方差计算各指标的权重,为对加权平均值进行处理后的数据矩阵,避免了数据处理结果受到极端值的影响,为后续降维提供好的数据保障.

2.1.2 熵权法数据筛选过程

采用熵权法进行数据处理的目的就是筛除掉对结果贡献率较低的数据,对加权平均值进行处理后的数据继续进行熵权法的数据筛选,式(4)中Ej为信息熵,rij为第i个数据的评价指标且满足 0 ≤rij≤1,式 (5) 中ωj为各个特征的权重,式(6)中Z(n×p)为数据预处理后输出的矩阵

对数据进行预处理标准化通常考虑标准差的影响,尤其是对被噪声污染的数据而言,噪声的标准差对数据的放大作用更显著,而没被噪声污染的数据其在标准化的过程中放大作用较小.因此,为数据集中每个特征计算出信息熵值而后利用信息熵计算得出特征权重,这样可以筛除掉作用小的数据以得到更高的降维精度.

2.2 基于加权核函数的主成分分析

改进的主成分分析过程引入加权核函数,通过选取核函数并构造多样化的核函数来提高数据处理效率,使得混合后的核函数性能更佳[16].

2.2.1 构造混合加权核函数

本文通过组合两种具有代表性的高斯径向核函数和多项式核函数的映射特性,构造一种混合核函数.该混合核函数拥有高斯径向核函数的局部特性,也拥有多项式核函数的全局特性,多项式核函数选择二阶.传统的高斯径向核函数、多项式核函数以及混合核函数表达式分别为[16]

由上述公式可以看出,涉及到的参数有高斯径向核函数参数σ、多项式核函数系数q和混合核函数的权重系数λ.文献[27]中通过训练和测试支持向量机找出效果最好的参数,但求解相对比较耗时.文献[28]中采用粒子群优化算法进行寻优,后期易陷入局部最优.针对参数寻优问题,本文提出一种改进的灰狼优化算法,减少主观经验选择的盲目性并在一定程度上提高算法的全局搜索和局部开发能力.由此依据加权核函数构建目标函数过程如下[9]

式(8)中γ用来对内积进行缩放;K为式 (9) 的加权核函数;式 (10) 中ω为超平面法向量,c为惩罚因子,ei为松弛变量;式 (11) 中yi为约束条件,ϕ(x) 为对应的函数映射,b为函数中截距变量;式(12) 中y(x) 为目标函数,αi为拉格朗日因子.

2.2.2 基于改进灰狼算法的混合核函数参数优化

GWO 算法是一种群智能优化算法.该算法的优化过程将包围、追捕、攻击三个阶段的任务分配给各等级的灰狼群来完成捕食行为,从而实现全局优化的搜索过程[29-30].改进的灰狼算法注重全局搜索与局部开发能力的协调,以便于较快获得全局最优

式 (13) 为标准GWO 算法中参数a的计算策略,其变化过程是线性递减的,但是在整个算法搜索过程中并非是线性变化的,因此在式 (14) 中提出一种非线性控制因子策略.式中t表示当前迭代次数,tmax为最大迭代次数.如图2 所示,当 |A|＞1 时,进行全局搜索,当 |A|≤1 时,进行局部搜索.由式 (15)可知,参数A随着控制因子a的变化而变化,因此在算法搜索过程中主要通过参数a的变化来完成.根据式(14),在迭代初期a的收敛速度较小,式(15)中A的值波动较大,避免了算法的早熟收敛,从而提升了算法的全局搜索能力.迭代后期a的收敛速度较大,算法有较强的局部开发能力.因此,改进的非线性控制因子策略能较好地协调算法的全局搜索与局部开发能力.

图3 为使用不同非线性控制因子策略的迭代结果,图中分别为利用不同控制策略对数据集CEC-2005 中函数F11[30]进行迭代的结果,横坐标为迭代次数,纵坐标为函数值,其中 G WOX为利用式 (14)的迭代结果,由结果可以看出本文提出的控制因子策略收敛速度快,迭代时间短[27].

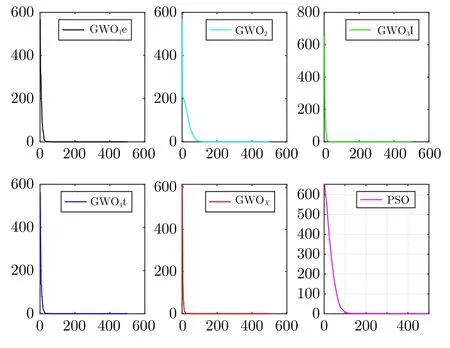
图3 不同控制因子策略的迭代结果Fig.3 Iterative results of different control factor strategies

灰狼在捕食猎物过程中的位置变化如式(15)～式 (17)所示

式中,A和C是系数向量,Xp是猎物的位置向量,而X表示灰狼的位置向量,D是一个矢量并且依赖于Xp,a为控制因子且在迭代过程中从2 线性减少到0,r1,r2是[0,1] 中的随机向量,式(14)～式(18) 为灰狼的位置变化,最后对位置求平均得到灰狼的最终位置X(t+1).灰狼位置更新的具体过程如式(18)～式 (20)所示[27]

其中,D α,D β,D δ为三个最佳解,X α,X β,X δ为本次迭代适应度前三的灰狼的位置,A1,A2,A3以及C1,C2,C3为每次迭代时产生的系数,X1,X2,X3为各灰狼的位置.

根据上述分析,可以得到改进GWO 的参数优化算法原理,如算法1 所示.其中,加权核函数中参数设置: 高斯径向核函数参数σ∈[0.01,100],多项式核函数参数q∈[0.1,4],惩罚系数c∈[0.01,1 000],混合权重系数λ∈[0,1].基于改进的GWO 进行参数优化的流程如图4 所示.

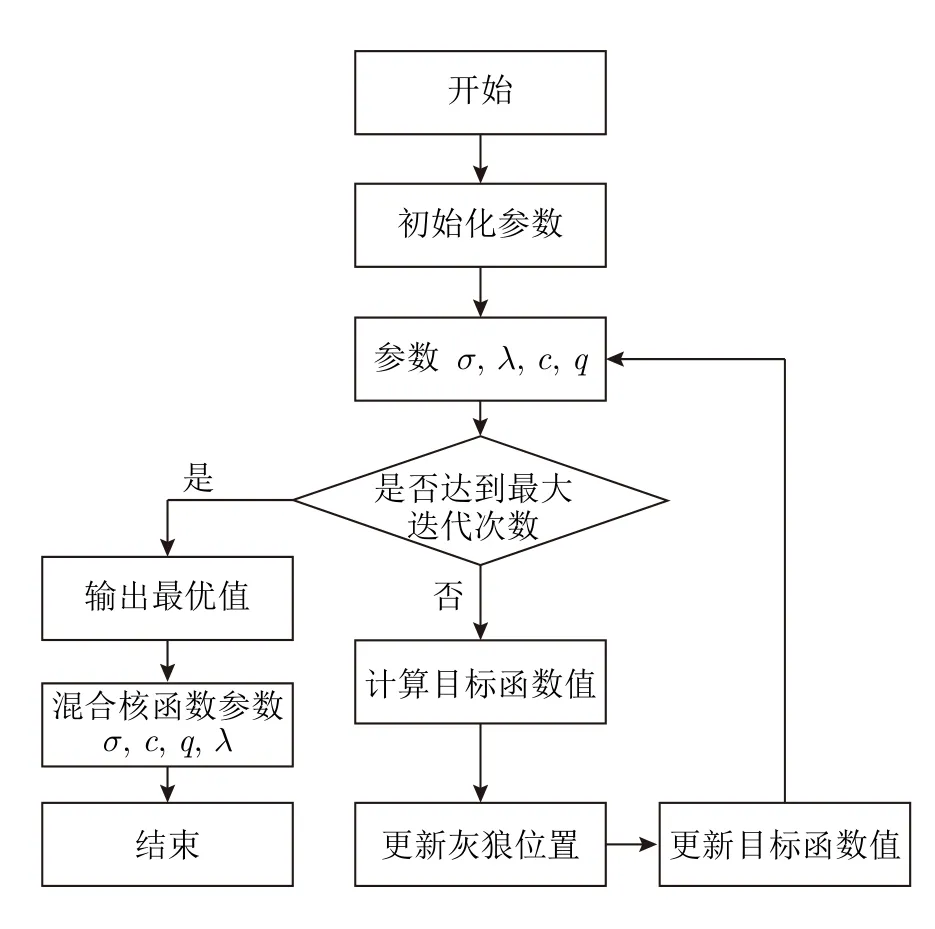
图4 GWO 参数优化流程图Fig.4 GWO parameter optimization flowchart

算法1.改进的GWO 参数优化算法

1) 初始化种群规模N,随机产生初始化种群,初始化t=0,初始化a,A,C,σ,λ,c,q等参数;

2) 计算种群中每个个体的适应度,将适应度排名前三的个体分别记为X α,X β,X δ;

3) 由式 (14)～式(17) 计算种群中其他个体与X α,Xβ和X δ的距离,根据式(18)～式(20)更新个体位置;

4) 更新算法中a,A,C,σ,λ,c,q等参数;

5) 判定算法是否满足收敛条件,如果满足,则算法结束;否则,令t=t+1,返回步骤 3).

2.3 独立成分分析与主成分分析的融合

对原始数据进行独立成分分析,n为样本量,p为数据维度.设有m条n维数据(n行m列),则构成n行m列矩阵X,X=HS,其中H是混合源分量的某个未知可逆方阵,S为解出的独立成分,ICA的目标是找到混合矩阵H,以便从观测数据中恢复原始信号H[31].

2.3.1 独立成分分析基本原理

1) 数据预处理,按行去中心化

2) 数据白化处理,去除数据集中所有线性相关性并沿所有维度归一化方差.

a) 求协方差矩阵

b) 奇异值分解,化简得到最终表达式

c) 得到原数据的白化数据Xw并将式(23)代入下式

d) 假设所有的数据源相互独立,那么也就可知

3) 利用信息论求解,找到一个旋转矩阵V,使得多重信息那么是条件独立的,则W=V D-1/2ET.

ICA 处理数据过程中,V是正交矩阵,为唯一未知的旋转矩阵,D为对角矩阵,对角线上的元素为对应的特征值,E 是对应的特征向量形成的一个正交基,U为奇异值矩阵,其中UTU=1,p(S) 表示概率分布.

2.3.2 改进ICA-PCA 的融合方法

本文提出一种ICA 和PCA 的融合模式,对两种降维结果进行相关性计算和分析,具体流程如图5 所示.

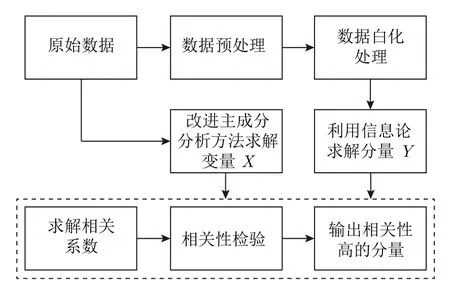
图5 ICA-PCA 融合过程图Fig.5 ICA-PCA fusion process diagram

文献[32]中提到使用皮尔逊相关系数和斯皮尔曼相关系数来描述两组变量的相关性,两者相比,皮尔逊相关系数需要数据服从正态分布,反之,斯皮尔曼相关系数适用于分布不明变量的相关性分析且没有过多数据条件要求,分别为改进后PCA 降维后得到的分量以及ICA 降维后得到的分量,因此,本文ICA-PCA 融合改进应用斯皮尔曼相关系数来处理和分析.式 (26) 为相关系数rs的计算公式

斯皮尔曼相关系数的取值范围为[-1,1],rs绝对值越大,相关性越强.斯皮尔曼相关系数rs＞0时,认为两组变量存在正相关;斯皮尔曼相关系数rs＜0 时,则认为两组变量存在负相关.依据rs相关系数的计算进行相关性检验,式 (27) 为具体检验公式,rs的分布可近似地用均值为0、标准差为的正态分布曲线表示,Z为正态检验值

通过计算Z可以根据正态分布密度函数求得检验值P,通过比较P值与0.05 之间的大小,可以判断r s＜0 的显著性.如果P值小于0.05,可以认为存在显著性的差异,即两者具有相关性.当样本数小于30 时,参照临界值表[33]该样本数所对应的斯皮尔曼相关系数临界值,当计算的斯皮尔曼相关系数大于临界值时,认为两者之间相关性是显著的,是有统计学意义的.

3 基于偏度和峰度的非高斯性判别

本文研究无人船航行观测数据的非高斯特征识别,因此,对降维后的数据基于偏度和峰度进行非高斯性判别.T 型多维偏度峰度检验是将多维数据转化为一维数据后进行检验,但该方法对数据分布有要求;而使用非参数检验方法不需要假设数据服从特定的分布,适用于各种类型的数据,例如KS检验.因此,本文使用T 型多维峰度统计量[8]并综合KS 方法[33]进行检验.

第一,对数据进行多元正态分布拟合[34]后得到均值向量和协方差矩阵;第二,使用KS 检验和T型多维偏度峰度检验来检验拟合后的数据是否符合正态分布;第三,使用KS 检验来检验拟合后的数据,检验两个样本是否来自同一分布,其检验统计量为KS 统计量;第四,如果KS 检验和T 型多维偏度峰度检验都表明数据符合正态分布,则可以认为数据符合正态分布,具体计算公式如下[34]

其中,x1,x2,···,xn为n个m维数据,µ是m维向量,表示随机变量的均值向量;Σ是n×n的协方差矩阵,f(xi;µ,Σ) 表示µ和Σ下样本xi的概率密度函数,l nL为对数似然函数,对对数似然函数求偏导数,令其等于零,解出参数µ和Σ的估计值,b1,b2分别为样本的偏度和峰度,分别为数据的三阶矩和四阶距.

4 仿真实验与验证

为验证本文所提方法对复杂情形下的USV 传感器受到不确定噪声的非高斯性/高斯性检测的优越性,进行仿真实验的平台配置: 硬件环境为CPU Intel(R) Core(TM)-i5-8265U 1.80 GHz,运行在Windows10 操作系统,运行软件为Matlab R2019b.为了保证实验的真实性和可靠性,本次实验在千岛湖水域对无人船的数据进行采集,以280 Hz 的频率采集无人艇在行驶中的正常数据集.数据集包括无人船位置数据和姿态角数据,具体如下:X方向的加速度ax;Y方向的加速度ay;Z方向的加速度az;围绕X轴旋转的俯仰角α;围绕Y轴旋转的偏航角β;围绕Z轴旋转的翻滚角θ.将以上6 个值作为待处理的值,从而很大程度地仿真了无人船在真实运动场景下受到噪声的实际情况,实验中使用无人船采集数据的环境如图6 所示,图6(a)为静止状态的无人船,图6(b)为运动状态的无人船.为评估所提出的改进方法在不同改进阶段的性能,本文通过对比相同数据集在不同方法下的结果,共做了5组实验,实验一验证数据预处理方法的必要性;实验二验证改进灰狼优化算法相较于其他优化算法的优越性;实验三对改进的ICA-PCA 方法进行分析并验证ICA 和PCA 联合的优势;实验四对比验证对改进方法降维后的结果进行非高斯性检测的效果;实验五验证整个方法在实际应用中的有效性.

图6 实际数据采集环境Fig.6 Actual data collection environment

4.1 改进后的数据预处理方法实验

实验一验证数据预处理方法的必要性.将本文提出的方法与EW-PCA 以及PCA 方法的结果进行比较,从而验证数据预处理对降维效果的影响.这里选取Arcene 数据集进行验证,Arcene 共700个样本,数据维度为10 000.K值表示降维后主成分的个数,在主成分个数更少的情况下,更大程度地保证了所含有的原有信息量.在相同贡献率时,本文提出的方法主成分个数K值能够取到更小,代表保留数据的能力更强.表1 为应用PCA、EWPCA 以及本文改进的PCA 方法对相同数据集降维的结果,观察表1 可见改进后的实验效果优于现有的方法.当贡献率同样都为95%时,PCA 方法的K值取110,EW-PCA 方法的K值取45,本文改进的PCA 方法的K值取36.在对相同数据集处理的情况下,本文提出的改进PCA 方法保留有用信息的能力更强.

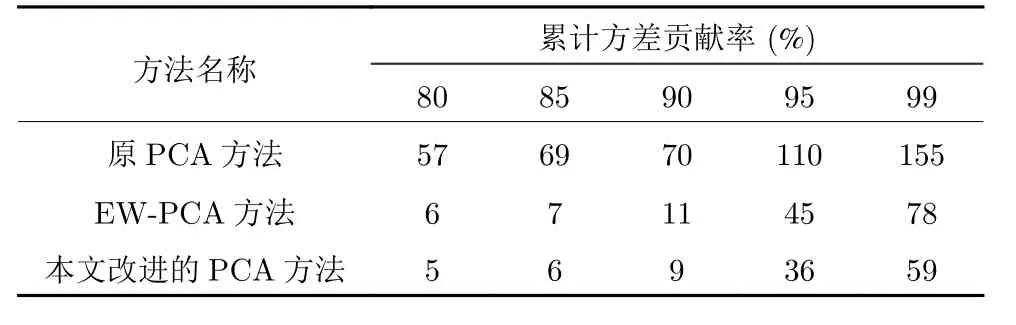
表1 降维结果对比表Table 1 Comparison table of dimensionality reduction results

4.2 改进灰狼优化算法的加权核函数寻优

实验二验证改进灰狼优化算法相较于其他优化算法的优越性.与近几年改进后的灰狼优化算法NGWO1等进行对比,将单峰函数、多峰函数以及固定维数的多峰函数三类函数分别进行测试,对PSO、GWO 以及NGWO1等优化算法结果从收敛性能、迭代次数等方面进行比较,实验的测试集使用CEC2005.图7 为单峰函数测试结果对比图,横坐标为迭代次数,纵坐标为函数值,从对比结果看,改进的GWO 算法相较于 N GWO1和PSO 收敛速度更快;图8 为多峰函数测试结果对比图,从对比结果看,改进的GWO 算法前期收敛速度慢,后期收敛速度较快;图9 为固定维度的多峰函数测试结果对比图,从对比结果不难看出,改进的GWO 算法具有收敛速度快以及迭代时间短等特点.因此本文方法在求解精度、收敛速度以及时间成本方面都有良好的性能,在一定程度上减少了主观经验选择的盲目性.

图7 单峰函数结果对比图Fig.7 Comparison chart of unimodal function results

图8 多峰函数结果对比图Fig.8 Comparison chart of multimodal function results

图9 固定维数多峰函数结果对比图Fig.9 Comparison chart of fixed dimension multimodal function results

4.3 改进的ICA-PCA 方法分析实验

实验三对改进的ICA-PCA 方法进行分析并验证其优势,使用主成分个数、累计贡献率和运行时间三个指标进行评价.通过比较本文方法和现有ICA-PCA 方法的结果,验证本文方法在实时性和降维效果等方面的优势.通过表2、表3 和图10,对比累计贡献率和运行时间两个指标,当保留48 个主成分时,累计贡献率达到了95%,相比改进之前的方法,保留有用信息的能力更强,时间成本更低.

表2 ICA-PCA 方法对比结果Table 2 ICA-PCA method comparison results

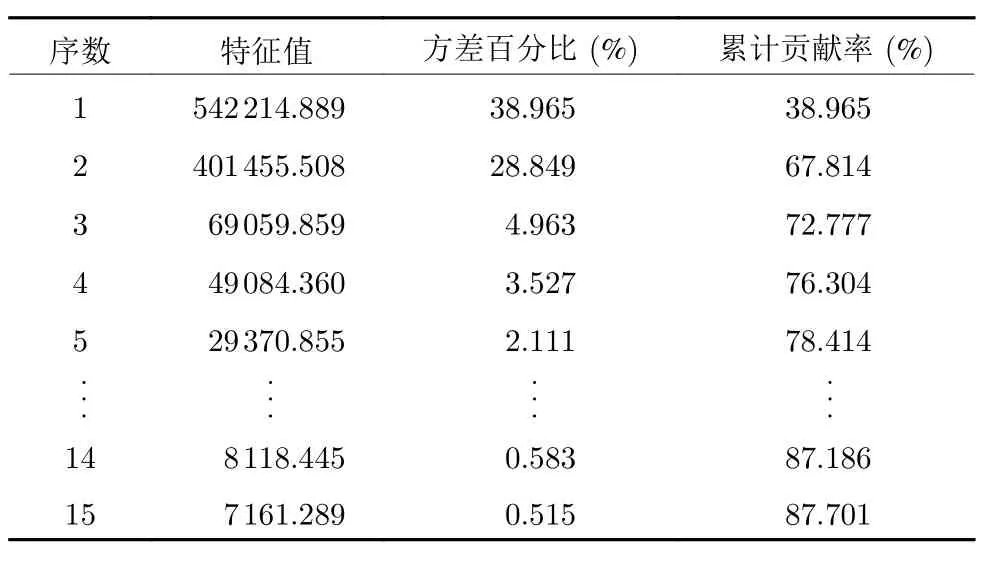
表3 降维结果Table 3 Dimensionality reduction results

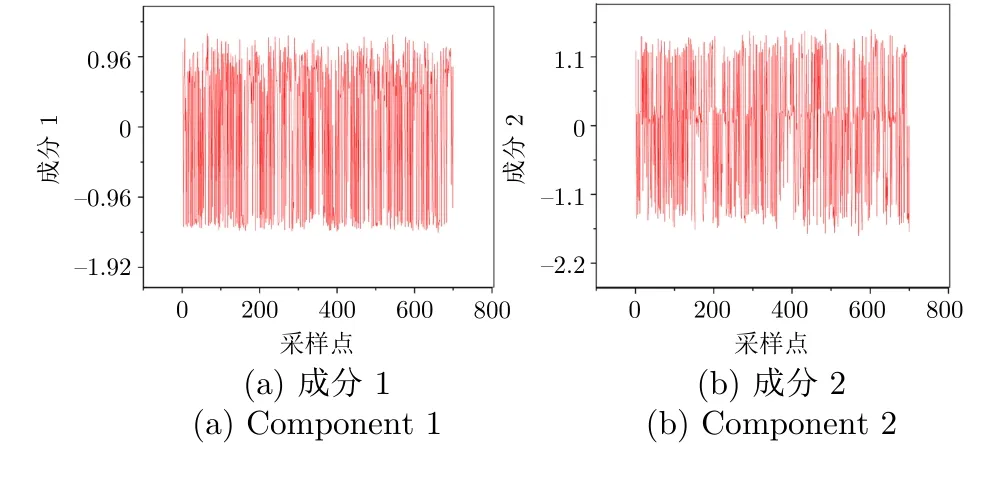
图10 降维主成分结果Fig.10 Dimensionality reduction principal component results

4.4 多维非高斯性检测方法的检测效果

实验四将降维后的数据的非高斯性判别结果与现有的非高斯性检测方法的判别结果进行比较,从结果的精确度和检测效果等方面进行比较.对原始数据集进行非高斯性检测,判断数据变量是否服从高斯分布,如果H0=0 且P在5%置信水平上,则过程变量服从高斯分布;反之,则服从非高斯分布.表4 为应用现有的非高斯性检测方法 Kolmogorov-Smirnov 检验和 Shapiro-Wilk 检验进行判别的结果.其中,统计量D为两条累计分布曲线之间的最大垂直差,描述两组数据之间的差异;统计量W为峰度,验证一个随机样本数据是否来自正态分布.当数据呈现出显著性P＜0.05 时,意味着数据不具有正态性.

表4 正态性检验结果Table 4 Normality test results

4.5 无人船航行姿态数据的应用验证

为了验证方法在实际应用中的有效性,对采集到的无人船航行姿态数据进行处理和检测.其中包括无人船进行圆形运动、矩形运动的线加速度、水平坐标和偏航角等信息.图11 为无人船圆形运动时X,Y,Z方向的速度变化,其中横轴代表采集样点数,纵轴为速度变化;图12 为降维后的结果;图13为非高斯性判别的结果,其中纵坐标频率描述数据集中每个数值出现相对频率的统计量.表5 中显示渐进显著性为0,则表明样本量的增加不会影响检测结果的显著性.

表5 非高斯检测结果Table 5 Non-Gaussian detection results

图11 三个方向的速度图Fig.11 Chart of speed in three directions

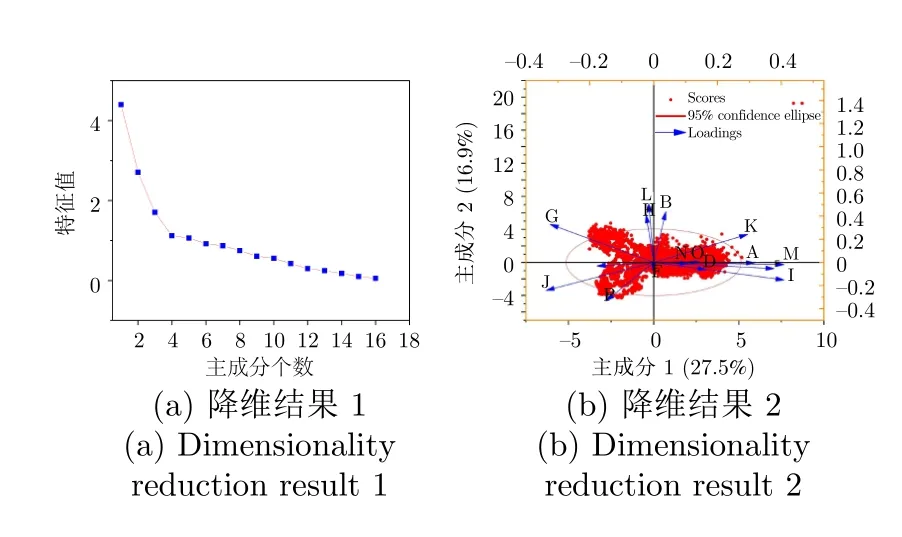
图12 降维结果Fig.12 Dimensionality reduction results

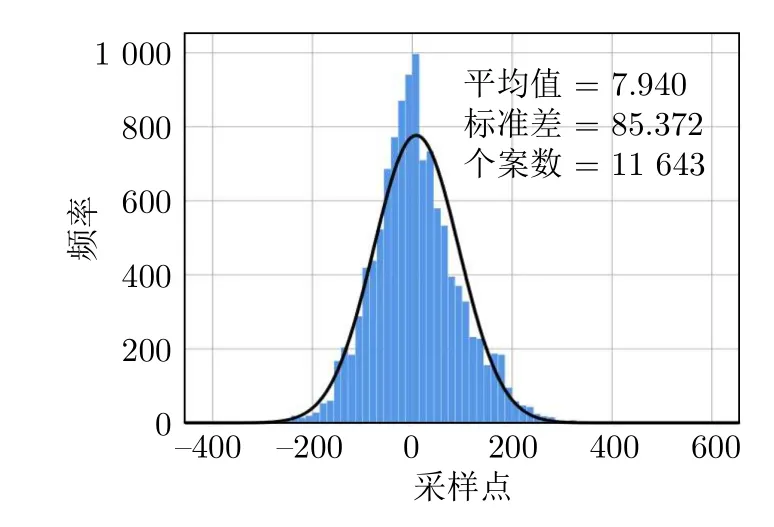
图13 检测结果1Fig.13 Test result 1

5 结论

针对复杂情形下传感器观测数据的非高斯性/高斯性检测判别问题,改进传统PCA 方法实现数据的降维处理,而后采用T 型多维峰度检验和KS检验方法进行非高斯特征的识别.该方法考虑到数据预处理的重要性、噪声数据的复杂性以及非线性非高斯的噪声对降维精确度的影响.实验验证改进后的方法能有效降低多维数据检测的复杂度,保证了最终结果的精确性和完整性.需要注意的是,本文分析时着重考虑对多维数据的降维处理,并未考虑更多基于偏度和峰度判别的方法,在下一步的研究中,将深入展开更细致化的研究,使方法在精度和完整性方面得到进一步提升.