消除全局层析反演累计误差的反向递推方法

薛 冈,熊鹰杰,孟庆利,单中强,云惠芳,杨 帆

(中国石油化工股份有限公司华东油气分公司,江苏南京210019)

随着地震数据处理技术的不断发展,层析反演方法的研究逐渐成为速度建模的重要研究方向。如何提高速度建模精度与效率是科研人员研究的热点,其中累计误差对深层速度的影响是实际生产中亟需解决的问题。

速度建模从早期叠加速度分析和迪克斯公式转换[1-2]到目前的网格层析,地震速度问题的研究取得了长足进展。层析反演在当今实际生产中得到了广泛的应用,基于射线理论的层析反演是根据偏移距域共成像点道集的剩余曲率来更新速度场[3-4],随后苑书金等[5]、BRANDSBERG等[6]使用角度域共成像点道集(ADCIGs)(以下简称角道集)进行层析反演;秦宁等[7-8]进一步研究了基于角道集的层析反演公式,加入了正则化与井资料的约束。相对于其它共成像点道集,角道集具有对速度的敏感性更高、不存在假象和在浅层区域的角度信息更多等优点,有利于提高浅层速度模型的精度[9-10],并且角道集携带了地震数据不同的入射角信息,更有利于速度模型的迭代更新[11-13]。常见的网格层析反演方法有两种:①无层位约束的网格层析[14-17]或立体层析反演;②有层位与断层约束的“层剥离”层析反演[18]。无层位约束的网格层析是根据工区背景或处理需求设置所需要的网格形状与大小,从而计算射线的走时信息;立体层析是基于局部相干同相轴,并将炮、检点位置处的斜率信息同时纳入层析反演数据空间,以减少反演多解性。这种方法只需要拾取局部相干同相轴的走时和斜率[19-21],且将反射问题转化为透射问题,巧妙回避了传统反射层析中速度与反射层深度耦合问题[22]。有层位约束的层析方法如CCG公司的HD-tomo,在速度突变区加入层位或断层,并改变网格大小进行局部或整体反演,以提高复杂模型的反演精度。这两种方法虽然可以对速度模型整体进行反演,但是他们的计算方法都忽略了浅层误差对中深层的影响从而导致深层成像不准确的问题[23-25]。

本文提出了一种从下至上逐层消除累计误差的计算方法,利用斯奈尔定律找出入射角与层速度的关系,计算每一层入射角的对应关系,逐层减去累计的深度误差。最后,根据每一层计算得到的深度误差来纠正后续叠前深度偏移成像剖面中反射层位的深度变化量,用以更新层位信息。最后,通过模型试算证明了算法的正确性,用实际资料测试证明了方法的适用性。

1 方法理论

1.1 常规层析反演原理

常规成像域层析反演依据当前层位的深度域共成像点道集同相轴的剩余曲率来计算深度误差,并通过时深转换得到走时残差,从而更新该层的速度值,该方法是推导射线旅行时残差与共成像点道集剩余曲率之间的定量关系式。如图1所示,角道集中不同的角度对应的偏移深度可以表示为[26]:

图1 深度残差

(1)

由此可推出深度残差Δz为:

(2)

其中,

(3)

式中:za是偏移深度;z0是零偏移距深度;γ为偏移深度与真实深度之比;d为入射角;di为角道集在i点的入射角;zai为控制点i对应的偏移深度;M为角道集控制点个数。图1是按照一定角度间隔计算的深度残差,实际反演中每一个角度都需要找出对应的深度残差,角道集中的角度越大对应的偏移距就越大,因此,大角度对应大偏移距信息,在速度误差不变的情况下传播时间越长,深度误差越大。

选取任意真实的反射界面位置RT,因速度扰动而得到的反射界面位置为Ri,根据图2中的几何关系可求出射线路径的改变量Δl为:

(4)

图2 深度误差累计原理

Tzi=Δzicosα

(5)

式中:α为地层倾角。将(5)式代入(4)式可得:

Δl=2Δzcosαcosd

(6)

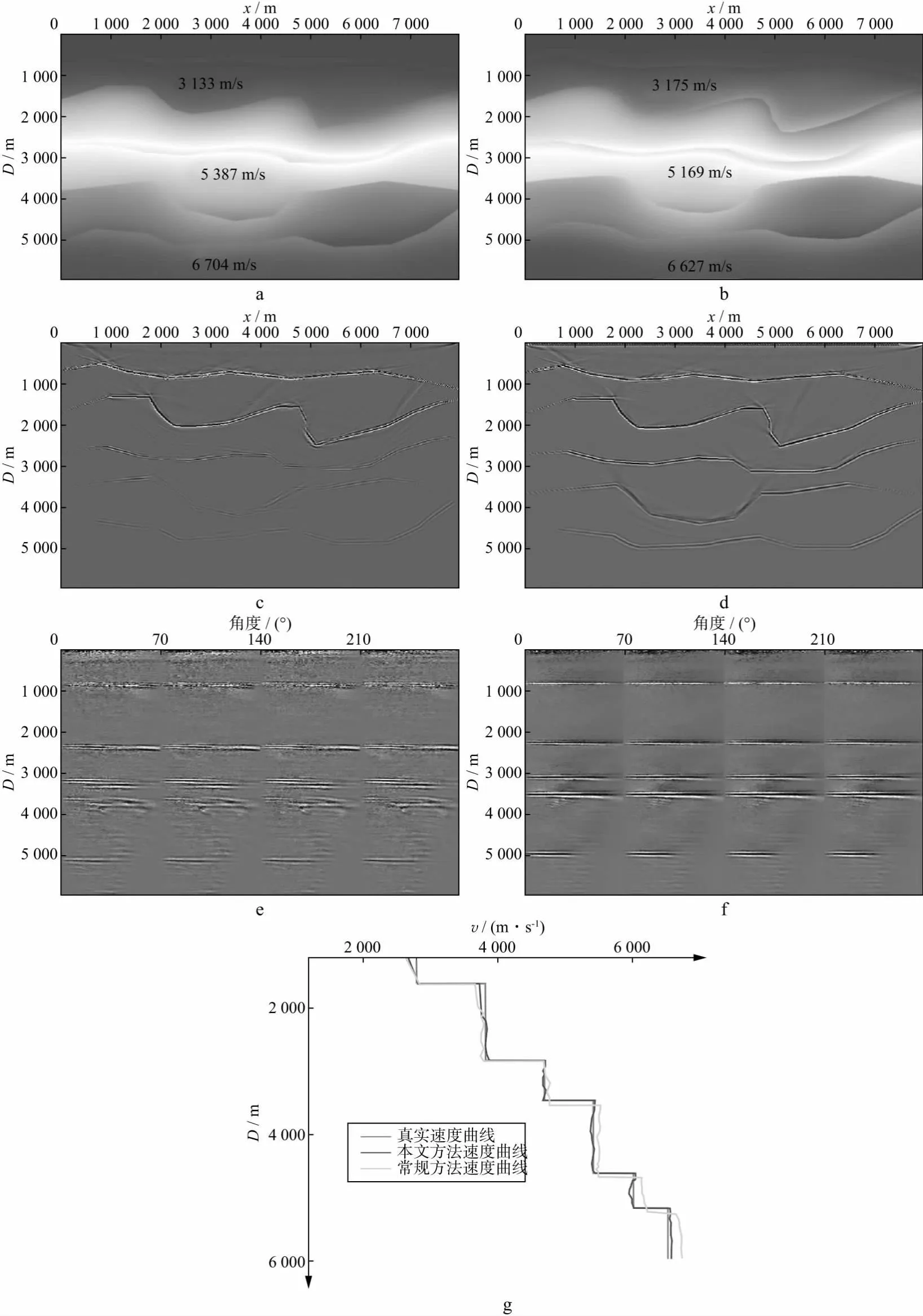
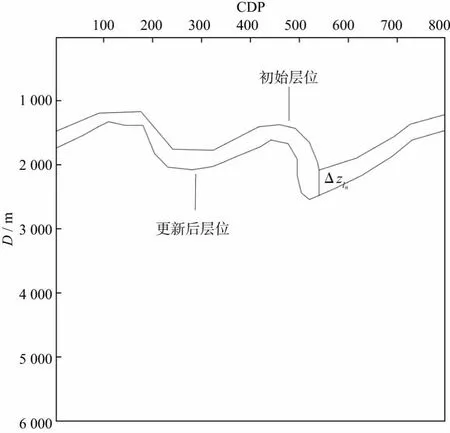
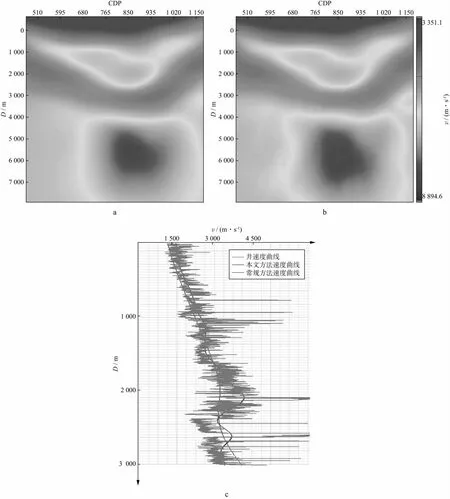
地下介质是多层且复杂的,目前常用的基于剩余曲率计算深度误差的层析反演方法每层均按这种方法来计算深度误差,然而这种计算方法忽略了射线在向下传播的过程中会携带上一层的深度误差,如图2所示。当理论速度小于实际速度时,扰动后的反射界面Ri1会比实际反射界面RT1的深度要浅,当射线继续向下传播时,由于扰动后的反射界面的入射点深度与实际层位相差Δz1,那么下一个反射界面在计算深度误差时就要加上第一层的误差。但每个反射层的速度都不相同,射线在向下传播的过程中会发生折射,到达下一层的入射角也会随之发生改变,因此,需要找出角道集的上下对应关系。假设v1

(7)

由于入射角小于90°,根据sin函数在第一象限单调递增,则可以证明角道集入射角di的上下对应关系为:

(8)

在层位信息中可以提取第n层反射界面Rin的深度,因此相邻反射界面的零偏移距深度之差可表示为:

z0n-z0n-1=ΔRin

(9)

式中:z0n,z0n-1分别为第n层与第n-1层零偏移距对应的偏移深度。

1.2 高效去除反演累计误差

针对累计误差这个难题,实际生产中的解决方法是增加速度模型更新迭代次数,直到浅层模型逐渐准确后,深层部分的累计误差就逐渐缩小直至达到预期精度。基于“层剥离”的层析反演虽然有层位约束且改善了误差自上而下的积累[27-30],但是每一层的速度更新后都需要进行一次偏移迭代,而且基于层位约束的层析反演在每次更新速度之后,反射层位在深度与形态上都会发生改变,之前拾取的层位都不再准确,需要重新拾取层位。多次迭代与逐层更新各有优劣,前者虽然反演效率高于后者,但在缺少层位与断层约束的情况下,很难还原地下深层部分的复杂构造。本文提出一种从下至上逐层消除累计误差的反向递推方法。

根据斯奈尔定律可以得到角道集从上至下的对应关系,并以此计算出射线向下传播过程中在上一层所积累的误差,根据图2中实际反射层位与扰动后反射层位的几何关系可由第一层角道集的入射角d1计算出第二层的实际误差为:

(10)

式中:z01,z02分别为第1层与第2层所对应的偏移深度。第n层的偏移深度zni与真实深度之比γn可表示为:

(11)

根据角道集从上至下的对应关系可以推出消除累计误差后第n层的深度误差Δzn为:

(12)

则公式(6)可改写为:

(13)

将公式(13)中的射线路径改变量按时深转换推导为时间残差:

(14)

式中:Δtn为消除累计误差后的走时残差;sn为第n层成像点处的局部慢度值。公式(14)的变量为单个矩阵元素,将其写成矩阵形式并代入最小二乘层析反演目标泛函为:

(15)

式中:E(s)是层析目标泛函;Δs为模型数据与观测数据的慢度差向量;L为灵敏度矩阵,其元素l为当前层位每条射线在网格内的路径长度。求取方式为:

(16a)

(16b)

其中,n(c)为当前射线位置,n0为初始射线位置,λ为梯度速度,v0为射线入射点速度。求出灵敏度矩阵后建立全局层析反演方程组:

(17)

将方程组进行全局求解得到所有层位的实际慢度更新量。

速度模型更新之后,再次偏移成像的剖面形态与地下层位的实际深度也会发生改变,在实际生产中往往需要解释人员重新拾取层位信息,费时费力。根据图2中的几何关系可得零偏移距道集在速度更新后的深度zu与之前偏移深度z0的关系式为:

(18)

式中:Δv是层析方程组求解的Δs的倒数,根据零偏移距深度的变化可以推出层位深度的改变量Δzl为:

(19)

角道集在更新一次速度后的形态与位置变化如图3所示。在速度得到修正之后再次进行偏移迭代会发现角道集的曲率变小,且实际深度也随着反射界面的归位而向下移动了Δz1,角道集的零偏移距深度和叠前深度偏移剖面的层位深度是相同的。实际的层位是每个反射层CMP点的深度坐标,因此可以利用角道集的深度变化来更新层位。这种变化并不是简单的向上或向下平移。如图4所示,由于每个CDP点的角道集剩余曲率都可能不相同,计算出的深度误差也不同,那么每个点的深度变化就会存在一定的差异,如图4中A点与B点的剩余曲率不同,深度误差就不同,从而导致更新后的层位与之前的层位在形态上发生改变。

图3 角道集更新前(a)、后(b)形态与位置变化

图4 不同层位点的深度变化量

2 模型试算

首先采用单斜模型验证自动更新层位方法的正确性,单斜模型如图5a所示。模型共有5个层位,每个层位的倾角各不相同,从上至下分别为10°,21°,31°,41°与51°。为了更加直观地验证层位更新的正确性,将真实模型整体乘以0.9并大尺度平滑作为初始模型(图5b),对初始模型与真实模型进行叠前深度偏移成像,并在偏移剖面上标定中深层的两套层位(图5c、图5d)。

图5 初始模型与真实模型及其偏移成像剖面a 真实速度模型; b 初始速度模型; c 初始速度模型偏移成像剖面; d 真实速度模型偏移成像剖面

用本文方法与常规方法进行三轮层析后的速度模型与标定的偏移剖面如图6所示。从速度模型不同层位的深度上可以初步看出本文方法得到的速度模型更接近真实模型。为了直观对比层位的变化,将4个偏移剖面的标定位置提取到同一坐标下,选择了5层中的两层进行误差对比(图6e),由对比结果可以看出,常规方法中部层位平均深度误差约为8.3%,深部层位平均深度误差约为11.5%;本文方法中部层位平均深度误差约为3.7%,深部层位平均深度误差约为5.5%。观察对比发现,本文方法速度模型对应的偏移剖面在标定位置比常规方法更接近真实模型。

图6 采用本文方法与常规方法进行3轮层析后的速度模型与标定的偏移成像剖面a 常规方法速度模型; b 本文方法速度模型; c 常规方法速度模型的偏移成像剖面; d 本文方法速度模型的偏移成像剖面; e 层位变化对比

为了进一步验证反向递推法消除累计误差的正确性,使用复杂模型进行测试,如图7所示。横向采样点800,纵向采样点600,采样间隔均为10m,真实速度范围为2000～7000m/s。为避免初始速度模型(图7b)对应的道集统一上翘或下弯,将真实速度模型(图7a)乘以某随机函数,再大尺度平滑,初始速度模型的偏移剖面(图7c)画弧严重,同相轴未归位且不连续,角道集上翘或下弯(图7d),这种现象在深层尤为严重。基于上述模型,采用常规网格层析方法与本文提出的递推消除累积误差方法分别进行测试,对层析结果采用RTM成像方法来验证建模的精度。

图7 真实速度模型(a)、初始速度模型(b)及初始速度模型对应的偏移成像剖面(c)和角道集(d)

图8为经过3轮偏移迭代后的常规网格层析反演速度模型与本文方法层析反演速度模型及其偏移成像结果。由图8可见,经过3轮偏移迭代之后,常规网格层析反演速度模型浅层部分的层位和真实模型已经基本一致,但深层部分速度层位的深度与真实模型不同,说明速度带来的误差影响了深层速度的准确性。常规方法浅层部分的道集已经被拉平,但中深层部分由于受到累计误差的影响,无法准确判断道集是上翘还是下弯,且随深度的增加道集质量也逐渐变差。偏移剖面上深层部分的同相轴杂乱且不连续,说明常规层析反演方法在更新速度模型时,只能优先将没有累计误差的浅层部分更新正确之后才能正确计算深层的误差,而前3轮的迭代过程中,中深层部分的深度误差是累计浅层部分的误差之后计算得出的,因此更新结果不正确。值得注意的是,在迭代次数增加的过程中,深层部分的速度值可能会出现偏大或偏小的情况,而且速度模型在横向上的变化通常是无规律的,这一建模难点在构造复杂地区尤为明显。在本次测试中,常规方法的中深层部分道集虽然是平整的,但道集质量差,说明该层是在累计误差的影响下被“拉平”,因此,该层的速度并非真实速度。由模型测试结果可以证明,只要中浅层部分速度不正确,都会影响深层部分道集与偏移成像的质量。

图8 经过3轮偏移迭代后常规方法与本文方法的速度模型及偏移成像结果a 常规网格层析反演速度模型; b 本文方法层析反演速度模型; c 常规层析反演速度模型的偏移剖面; d 本文层析反演速度模型的偏移剖面; e 常规层析反演速度模型的角道集; f 本文层析反演速度模型的角道集; g 两种方法速度与真实速度曲线对比

而本文方法层析反演速度模型(图8b)得到的层位形态与深度都与真实模型基本一致。本文方法在消除累计误差后,速度模型第2层与常规方法相差不足1%,但中深层部分的速度值的准确度比常规网格层析提高了3%左右,对比成像剖面发现,深层的成像有了明显的改善,同相轴清晰且连续,深层部分的道集已接近平整,最后将两种方法的速度模型与真实速度模型抽取相同位置的纵向曲线进行对比(图8g)可以看出,本文方法速度模型的纵向变化趋势与真实速度模型更加一致。

本文方法在每轮迭代的同时也会更新层位的深度信息,利用公式(19)改变对应CDP点的层位深度,经过3轮迭代层位的改变量如图9所示。第n个CDP点的深度更新量用Δzln表示,根据不同点位道集的剩余曲率的差异,层位在更新之后形态会发生一些改变,多次更新之后形态会逐渐接近真实层位,节省了多次拾取层位信息的时间,提高了层析反演的效率。

图9 层位更新原理

3 实际数据应用

四川盆地东南缘构造复杂区地表、地下呈现“双复杂”地质特征,地表灰岩出露,高程变化大,地下逆断层发育,部分地区目的层高陡构造特征明显。在该地区采集的某三维地震数据整体信噪比低、地震波场复杂、速度建模困难。在该工区应用本文方法开展速度建模工作,测试数据的最大偏移距为6000m,测线横向CDP点数为1320,间隔为20m,最大偏移深度为11250m。采用Kirchhoff叠前深度偏移进行成像以及角道集的提取,本文方法迭代次数为9次,常规方法迭代次数为17次,且在迭代过程中需要重新拾取一次层位信息,本文方法每次迭代会自动更新层位信息,最终获得的速度模型如图10所示,两种方法速度模型的形态在浅层的改变并不明显,但本文方法得到的速度模型(图10b)在深层的形态以及速度值与常规方法(图10a)的差异较大且更接近地下构造的实际形态,与井曲线的趋势对比(图10c)进一步证明了本文方法得到的速度更准确。

图10 常规方法(a)、本文方法(b)速度模型以及两种方法速度曲线与井曲线对比(c)

利用两个速度模型进行Kirchhoff叠前深度偏移,角道集与偏移剖面如图11所示。经过多轮迭代,常规方法与本文方法的浅层道集都已经被拉平,但常规方法的深层道集(图11a)不仅上翘且不连续,而本文方法在消除深层的累计误差后得到的道集(图11b)在深层部分已经基本平整且连续,证明速度值正确。从偏移结果来看,常规方法偏移剖面(图11c )在深层向斜构造区域成像不清晰,且同相轴连续性差,本文方法的偏移剖面(图11d)在该区域成像质量与连续性有明显改善,且整体成像效果优于常规方法。

图11 基于常规层析反演速度模型与本文层析反演速度模型得到的角道集与偏移剖面a 角道集(基于常规速度模型); b 角道集(基于本文速度模型); c 叠前深度偏移剖面(基于常规速度模型); d 叠前深度偏移剖面(基于本文速度模型)

4 结论

1) 针对层析反演速度误差逐层积累的难题,本文从剩余时差的计算原理出发,推导出降低累计误差的计算方法,并用修正后的角道集剩余曲率计算得到真实的深度误差来更新层位,提高层析反演精度的同时,也提高了反演效率。

2) 本文提出的反向递推方法有效降低了层析反演累计误差,能够给出更为准确的速度模型,基于速度模型偏移获得的深、浅层部分的层位形态和真实模型的形态比常规网格层析反演更为准确。

3) 模型测试结果表明,采用本文方法建立的速度模型的反演精度比常规层析反演方法提高了1%～3%。在提高层析反演精度的同时,自动修正层位深度,也提高了反演效率。四川盆地某工区实际数据主要目的层为向斜构造,深度范围是2871～6098m,经过钻井资料证实,基于常规层析反演速度模型偏移的成像剖面深度误差为60～90m,基于消除累积误差后的速度模型获得的偏移剖面深度误差为30～65m,精度明显提高。