低信噪比地震数据图像结构引导去噪方法与应用

郑启明,李 琦,都小芳,吴高奎

(1.北京派特杰奥科技有限公司,北京100044;2.中国地质大学(北京)海洋学院,北京100083;3.中石油东方地球物理公司研究院,河北涿州072751;4.中石化石油勘探开发研究院,北京102249)

基于地震资料刻画断层、裂缝等结构特征,对于发现和描述油藏具有重要意义,可支撑决策最佳开发方案、减少探井风险,提高石油勘探成功率。然而,在地震勘探区域,由于地质结构比较复杂,断裂带的地层形态多变,因而常导致采集的地震数据信噪比较低,使得地震数据处理、解释十分困难。高品质的地震资料是高质量解释、油气储层精准预测的重要依据和保证。因此,在地震数据处理时需要采用有效的去噪技术来提高地震资料的品质和可靠性。地震资料处理和解释人员探索了一系列的地震数据滤波技术以提高地震资料信噪比,如频率-波数域滤波、时域中值滤波等[1],这些技术可以有效去除地震数据中的部分噪声,从而提高地震资料解释和油气储层预测的准确性。相比通用的图像处理算法,地震数据处理更关注利用反射同相轴的横向一致性,处理过程中可能会压制倾斜断层阴影部分的幅值、破坏小尺度断层和裂缝等非连续性的结构信息,导致错误匹配断层两侧的同相轴。因此,进一步探索研究可以保护断裂、裂缝、尖灭等地质信息的叠后地震保边去噪技术对地震解释工作尤为重要。

为更好地利用地震反射的局部信息,LUO等[2-3]首次将保边光滑滤波的思想引入地震资料解释性处理领域。采用Kuwahara多窗分析技术得出,此类方法可以考虑局部结构信息设计自适应光滑滤波器[4-5],在提高信噪比的同时,保护地震图像中的有效地质信息。此后,国内外学者引入基于各向异性扩散滤波的构造导向滤波技术[6-10],通过结构张量评估局部结构走向、计算各向异性算子,设计增强地震资料沿同相轴方向的信噪比、抑制断点位置光滑强度的自适应滤波器。在此基础上,国内外学者优化了相关算法,提高了结构张量评估局部层位走向的有效性[11-16],通过偏微分方程的近似解法提高了计算效率[17],并将相关技术扩展应用到三维地震数据的处理[18-20]。考虑到扩散滤波的有效性依赖于结构张量的准确估计,HALE[21]提出了引入高度自适应的双边滤波技术来实现保边光滑处理的方法,但该方法的计算代价相对较高。国内学者也探索了在变换域[22-24],如曲波域、变分模态域或多道奇异谱上的数据滤波去噪处理技术。TRINH等[25]提出了利用Bessel函数逼近各向异性Laplace滤波的结构导向光滑算法;在图像处理领域,HE等[26]提出了利用引导图像滤波进行自适应保边光滑处理的方法,计算效率显著高于双边滤波方法,该方法尚未在地震数据处理中广泛应用。此外,结构导向光滑滤波技术在全波形反演中也具有较明显的应用效果[27-28]。近年来人工智能技术飞速发展,高性能滤波算法[29]、神经网络地震数据去噪方法[30-31]和智能化断层表征技术[32-33]也得到了深入的探索。

在前人研究的基础上,将“二维图像滤波”首次扩展应用到二维或三维地震数据处理中,该计算过程有别于传统的二维图像滤波。为抑制随机与相干噪声、增强地震反射同相轴的一致性,建立了双边显式加权滤波器的框架,引入了分时窗的引导滤波核函数与正规化算子,建立输入与输出的目标方程,利用线性回归显式求解方程系数,迭代计算直至收敛。该算法采用高效率的保边光滑处理,使得处理后的地震资料能更加准确地刻画地质结构,从而更好地服务于地质勘探开发。

1 图像结构引导滤波原理

针对地震数据去噪开发的滤波器可分为非平均滤波器和加权平均滤波器,前者以中值滤波为代表,其滤波过程一般为非线性过程,后者可进一步分为显式滤波器和隐式滤波器。显式滤波器通过设计滤波核函数,然后根据核函数对待处理的数据进行加权平均实现特定滤波的目的,其中较典型的有均值滤波、高斯滤波。在地震数据处理中,以隐式加权平均的扩散滤波方法较为常见,其将包含在矩阵中的滤波器作用于待处理数据,可以较为直接地在矩阵中引入各向异性参数并求解隐式矩阵来实现结构导向滤波。需要注意的是,各向同性扩散滤波与高斯滤波是等价滤波器。

定义问题Iout=Iin+n,其中,Iin,Iout,n分别为含噪声数据、去噪后的数据和噪声。参考显式加权平均滤波器的设计思路,可利用线性加权平均定义滤波核函数:

(1)

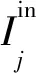
(2)

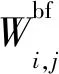
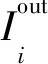
(3)

其中,k为窗wk的中心坐标,(ak,bk)是表征该线性关系的参数,假定其在窗wk中为常量。若输入数据Iin和输出数据Iout的差异为随机或相干噪声,则确定参数(ak,bk)的最小化目标函数为:

(4)

其中,ξ是正则化算子系数,用以确保ak的解在可接受的数值范围内。利用线性回归算法,可显式地求解(ak,bk)的值,即:

(5)

(6)

分时窗处理过程中,由于在时窗交叠区的输出数据Iout具有非唯一性,因此,在同一点处多个交叠窗的平均输出表达式为:

(7)

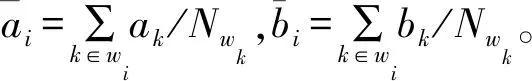
(8)

传统的双边滤波器可以利用引导数据通过显式加权平均进行保边结构光滑,其核心在于使用线性加权平均滤波器,可以引入滤波核函数。引导滤波器采用同样思想,但通过构建最优化问题引入了隐式的加权平均,通过线性最优化解获得了引导滤波器算子,同时在优化问题中引入正则化算子形成超参数,可控制对于边界结构的敏感程度。

以上推导过程适用于二维或三维地震数据体。在具体应用过程中,需要准备引导数据G(原始输入数据或滤波处理后的窄带高信噪比数据),试验确定半窗宽度r和正则化因子ξ两个参数。当r和ξ变大时,处理后的数据具有更强的光滑效果,可能会损伤地震反射的断裂结构信息,实际计算中需要根据保边处理的目的与需求,综合考虑确定合适的处理参数。由公式(5)至公式(7)可知,该算法可多次迭代应用方框滤波器实现地震数据的去噪处理,自动具备O(n)的计算效率。

具体应用于实际地震数据处理时,采用以下技术流程:

1) 准备待处理的地震数据Iin(二维或三维地震数据)、结构引导数据G(可以与Iin相同)、设置算法参数半窗宽度r和正则化因子ξ;

2) 计算f(Iin),f(G),f(Iin·Iin)与f(Iin·G),其中,f为均值滤波器;

3) 计算参数a=[f(Iin·G)]/[f(Iin·Iin)-f(Iin)f(Iin)+ξ];

4) 计算参数b=f(G)-af(Iin);

5) 计算滤波后的数据Iout=f(a)Iin+f(b)。

此流程主要计算6次均值滤波,由于均值滤波器可以使用方框滤波器的方法构建,因此本流程具有O(n)复杂度的计算效率。

该流程中结构信息的引入依赖于结构引导数据G的选择。引导滤波应用过程中利用均值滤波器提取G的结构信息。假如G由多个均质的区块构成,那么引导滤波会在各个区块内分别进行操作,而不会在光滑区块的边界进行均值滤波,从而有效保留边缘信息,实现保边滤波的效果。若G是输入数据本身,则引导滤波器会强化数据本身的走向或者倾斜结构,同时具有保留边界、突出主要结构的功能。导向滤波器中的引导数据G的选取可根据具体应用调整,本次研究选择输入数据作为引导数据,是较为直接和有效的方法。

2 模型数据测试

为验证图像结构引导滤波算法的稳定性与结果的可靠性,对比该算法与传统滤波器及主流滤波器的优劣,基于Marmousi模型通过卷积15Hz主频的Ricker子波和反射系数,在设计的二维合成地震剖面(图1a)中加入一定噪声得到信噪比(signal to noise ratio,SNR)约8dB的含噪数据(图1b),以此评估后续各类滤波算法的去噪效果。其中,SNR定义如下:

(9)

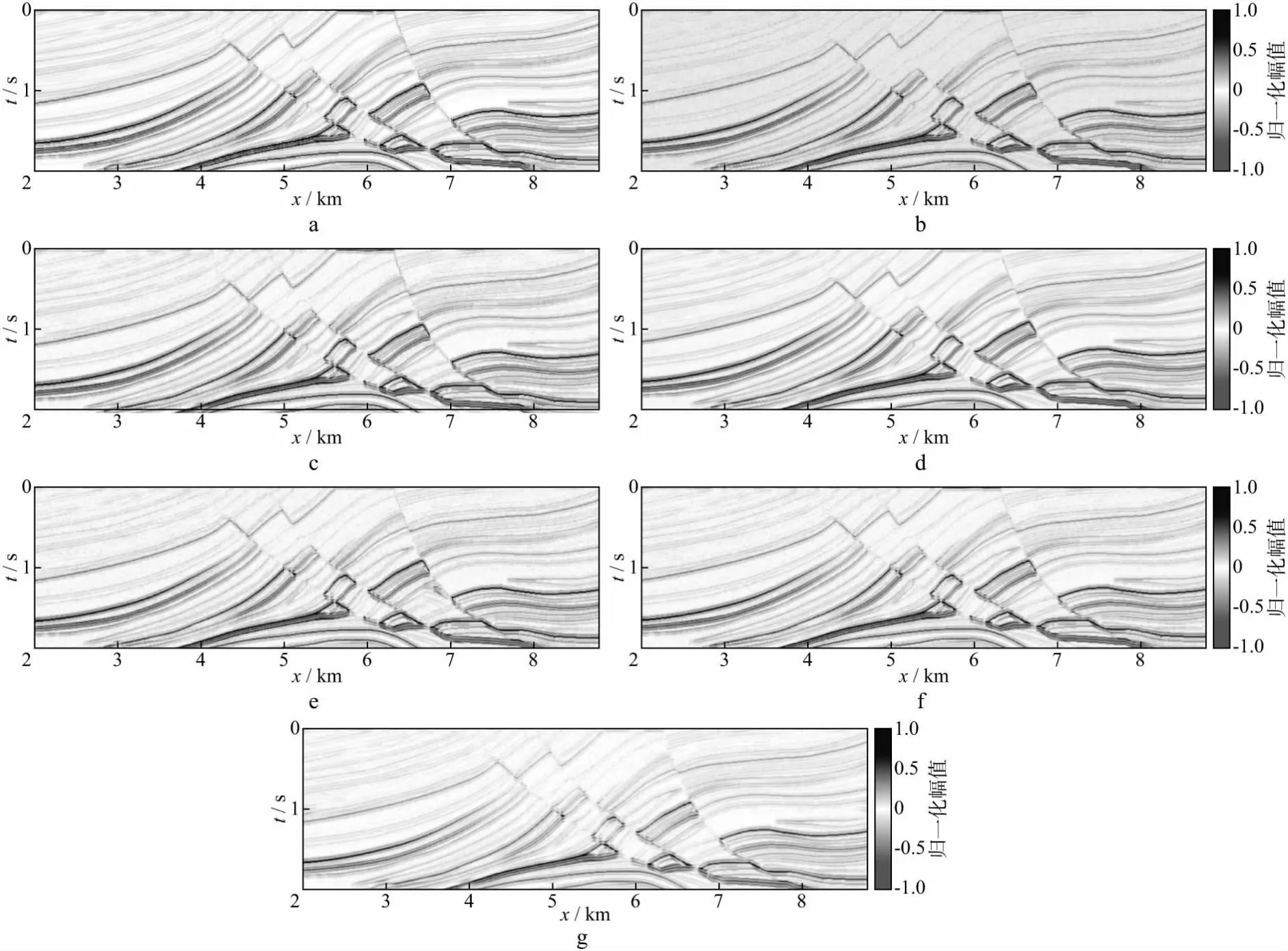
图1 基于Marmousi模型的合成地震剖面去噪测试对比a 无噪剖面; b 含噪剖面; c 图像结构引导滤波后的结果; d 构造导向滤波后的结果; e 中值滤波后的结果; f 均值滤波后的结果; g 高斯滤波后的结果

其中,Isignal表示不含噪声的有效信号,Isignal+noise表示含噪声的信号,SNR表示计算得到的信噪比。

为方便对比不同方法的去噪效果,试验中选用了相同的半窗宽度,其中图像结构引导滤波与构造导向滤波皆以原始数据本身作为引导数据提取结构张量进行处理,含噪地震数据的自适应引导图像滤波、构造导向滤波、中值滤波、均值滤波和高斯滤波的处理结果分别如图1c至图1g所示。

由模型去噪结果可知,图像结构引导滤波(图1c)、构造导向滤波(图1d)、中值滤波(图1e)、均值滤波(图1f)、高斯滤波(图1g)均有效消除了部分噪声,提高了模型数据的信噪比。前两种方法的信噪比由8.00dB分别提高至18.31,14.77dB,与构造导向滤波相比,图像结构引导滤波的信噪比高约4dB,对地层边界具有更好的保护作用;而后3种方法的信噪比由8.00dB分别提高至9.19,9.58,10.09dB,信噪比虽有所提高,但在一定程度上模糊了地层与断裂的反射边界。

为便于清晰展示上述去噪效果,图2更详细地对比了不同方法分离的噪声剖面。图1与图2的截断幅值不同。在层位相对平缓的区域,如距离为8km,时间为1s处,图像结构引导滤波和构造导向滤波均较好地保持了地震数据的结构信息(图2b、图2c),而中值滤波、均值滤波和高斯滤波因过度光滑破坏了有效地震反射的真实结构信息(图2d、图2e、图2f)。针对本合成数据中其它斜率较大的结构,从噪声剖面可知,构造导向滤波(图2c)保留边界的能力相对中值滤波(图2d)、均值滤波(图2e)和高斯滤波(图2f)更强,但是图像结构引导滤波(图2b)更好地保留了地震反射细微的结构。总之,相比其它处理方法,图像结构引导滤波不但能有效抑制噪声,而且在处理方法与计算效率上也更加简单高效。

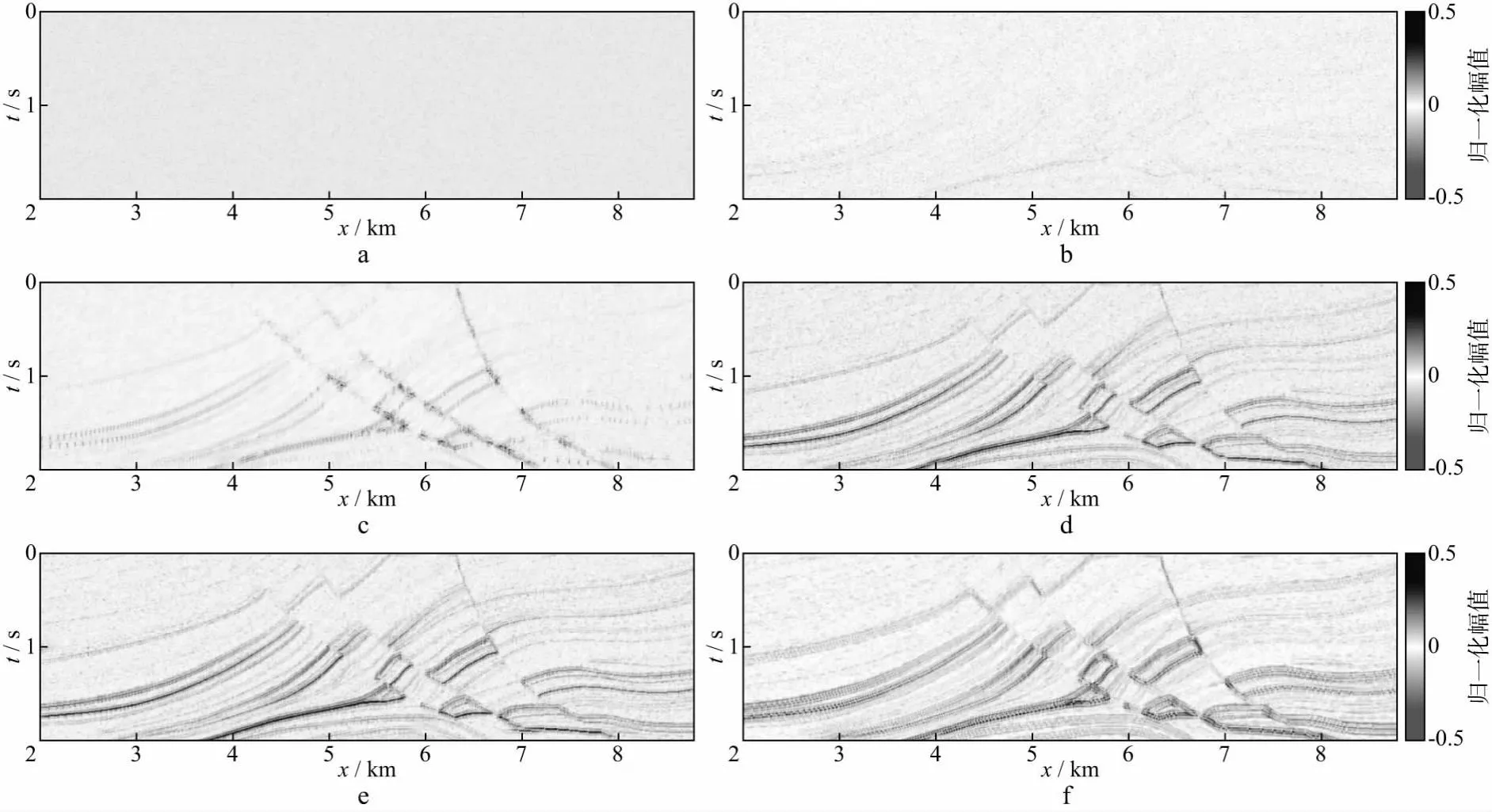
图2 不同方法分离的噪声剖面对比a 原始噪声; b 图像结构引导滤波; c 构造导向滤波; d 中值滤波; e 均值滤波; f 高斯滤波

3 实际应用效果

以信噪比较低、含有断层的三维地震数据为例,利用含噪数据为引导,基于核滤波函数自适应地对其进行滤波处理。图3和图4分别为自适应滤波前、后不同频带三维地震剖面和沿层振幅切片。由图3和图4可见,自适应滤波处理前,低频地震数据的地震剖面和沿层振幅切片中存在明显低频噪声(图3a、图4a);受噪声影响,中频信号与小尺度断层反射信息相混叠,导致属性边界模糊不清(图3c、图4c);高频地震数据的地震剖面和沿层振幅切片中的高频有效信号受噪声影响更加严重,信噪比极低,同相轴连续性极差(图3e、图4e)。

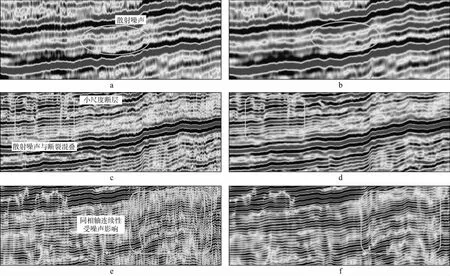
图3 自适应滤波前、后不同频带三维地震剖面a 低频含噪信号; b 低频图像结构引导滤波结果; c 中频含噪信号; d 中频图像结构引导滤波结果; e 高频含噪信号; f 高频图像结构引导滤波结果

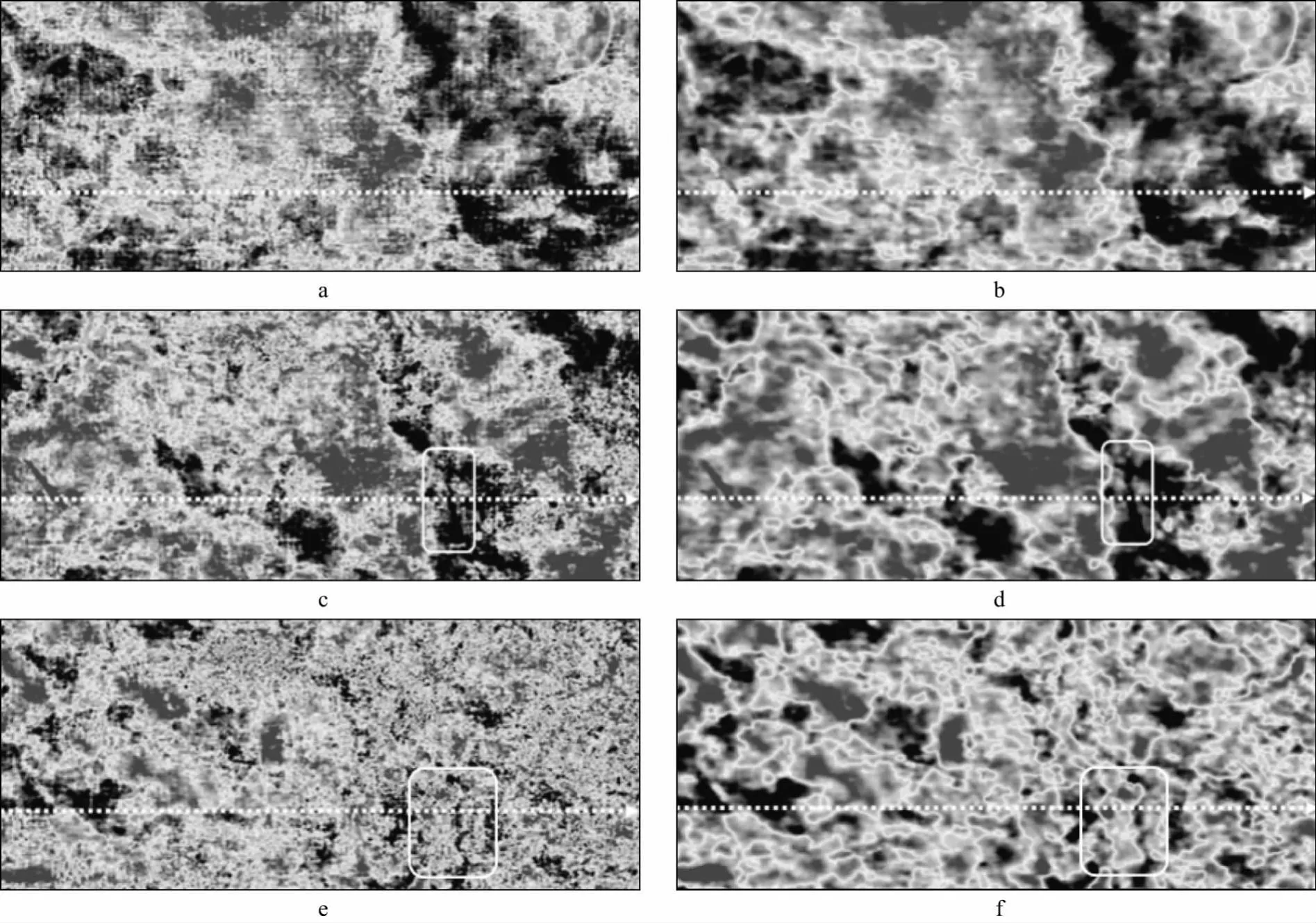
图4 滤波前、后不同频带沿层振幅切片属性a 低频含噪信号; b 低频图像结构引导滤波结果; c 中频含噪信号; d 中频图像结构引导滤波结果; e 高频含噪信号; f 高频图像结构引导滤波结果

与图3a、图4a低频信息相比,图像结构引导滤波很好地压制了低频数据中的散射噪声,同时很好地保持大尺度断层的错断边界(图3b、图4b);其次,对比图3c、图3d和图4c、图4d可见,本文滤波处理方法可有效保边光滑去除噪声、提高信噪比,同时保持小尺度断层、沉积体边界的有效反射信息(图3d、图4d 标识区域);对比图3e、图3f与图4e、图4f可见,本文方法可自适应利用高信噪比优势频带信号作为引导图像数据,有效压制高频噪声、提高地震同相轴连续性与信噪比(图3f与图4f方框区域),有助于解释人员提高小断层和地震属性的解释与描述精度。

构造导向与图像结构引导滤波的全频带处理结果如图5所示。在含噪地震数据(图5a)上提取结构张量的倾斜构造导向滤波结果如图5b与图5c所示;以含噪数据自身为引导的图像结构引导滤波处理结果如图5d 所示。由图5可见,采用构造导向滤波与自适应图像结构引导滤波处理后的地震剖面信噪比显著提高,除大断层特征更加明显之外,小断裂的细节更加清晰。对比图5b、图5c可见,当构造导向滤波的相关半径较大时,会导致计算效率降低、横向保边结果略差;当相关半径较小时,局部产生相干噪声异常(图5c中红圈),散射噪声压制不彻底(图5b、图5c黄框)。

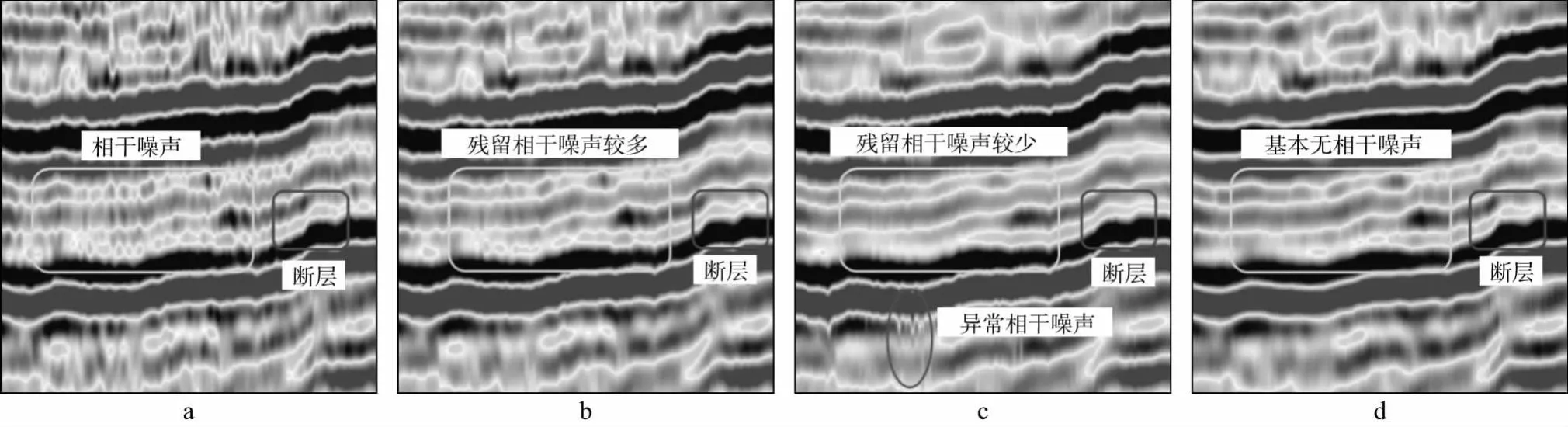
图5 原始地震数据、构造导向滤波与自适应图像结构引导滤波结果a 原始地震数据; b 小半径构造导向滤波结果; c 大半径构造导向滤波结果; d 自适应图像结构引导滤波结果

自适应图像结构引导滤波可较为彻底地压制相干噪声、保护有效反射信号(图5d)。在算法上,其相比于构造导向滤波,可自适应地从原始含噪地震数据中优选引导图像数据与处理参数,无需象构造导向滤波那样为获取倾角信息而多次调整参数来计算结构张量并重复进行引导滤波;在计算效率上,其利用的线性函数可有效降低计算复杂度、提高运算效率,计算代价仅相当于数次均值滤波。

对原始地震数据、构造导向滤波和自适应图像结构引导滤波结果分别利用相同的特征值参数提取相干体剖面与沿层相干属性信息进一步评价处理效果(图6、图7)。

图6 原始地震数据、构造导向滤波与自适应引导图像滤波后相干体剖面a 原始地震数据相干体剖面; b 小半径构造导向滤波后相干体剖面; c 大半径构造导向滤波后相干体剖面; d 自适应图像结构引导滤波后相干体剖面

图7 原始地震数据(a)与自适应图像结构引导滤波后(b)沿层相干属性

在断裂位置附近,对比原始数据与不同构造导向半径获取的相干结果(图6a、图6b与图6c),因受散射噪声影响,导致其对断层的分辨能力大大降低,给后续的解释工作造成困难。此类污染主要由于断裂带附近的地震反射资料信噪比低、同相轴的连续性不够明显,导致计算的相干体属性难以区分地震层位与断裂结构特征;与其它方法相比,本文方法可有效压制地震数据中的噪声,因此可获得信噪比更高的相干体,从而能够更加清晰地描述复杂的断裂结构(图6d);同时,沿层相干属性也能够很好地描述细微断裂结构,多级断裂在横向上的层次关系也更加清晰(图7)。该结果有助于后续的层位与断裂解释。

4 讨论

图像结构引导滤波的引导数据G的设计具有关键作用。传统的构造导向滤波需要利用结构张量等方法,显式地提取结构体在某个区域内的倾角和方位角,而本文方法的引导图像数据不需要显式表征结构倾角和方位角,只需要其梯度具备与期望输出图像Iout一致的边界信息。同时由于其具有滑动窗实现的特点,以含噪声的图像作为引导图像,可在有效保留结构边界的前提下压制随机噪声。然而,在实际地震数据处理中,相干噪声、散射噪声是影响地震图像质量的关键,仅以含噪图像作为引导可能会增强相关噪声的强度。但由于引导图像本身设计的灵活性,可采用以下步骤压制相干噪声和散射噪声:①先采用自引导的方式压制随机噪声;②再利用均值、中值、高斯或构造导向滤波处理剖面,获得边界受到一定破坏但相干、散射噪声得到压制的剖面;③再以步骤②的输出结果作为引导图像处理步骤①的输出结果。但是,此方法仍具有一定局限性,其有效范围仅限于相干或散射噪声相对较弱的状态,否则其它滤波器在压制相干或散射噪声时会过度伤害主要结构信息。需要在未来工作中进一步改进图像结构引导滤波,形成自适应压制相干或散射噪声的方法。

5 结论

在进行地震资料的断层、裂缝解释时,噪声的存在会明显影响解释精度。通过引入图像结构引导滤波方法,能自适应地提取有效地震结构引导信息,快速、有效地对地震数据进行保边、保幅去噪处理。图像结构引导滤波基于理论推导可通过方窗滤波器实现,对于大尺度地震数据不存在显著的计算瓶颈,具有O(n)的计算效率,相比工业界更常用的构造导向滤波器也有一定优势。含噪合成模型数据的处理分析结果证实了图像结构引导滤波可保留反射结构边界、有效压制噪声,结果显著优于常规非结构性光滑滤波器。针对实际地震数据的处理,利用引导图像可灵活设计引导特征,在一定程度上压制相干噪声与随机噪声,提高地震数据信噪比,增强地震反射同相轴的一致性、保留并突出断裂与地层反射的非连续特征。计算的相干属性较其它方法断裂结构特征更加清晰,地质规律更加明显,进一步证明了方法的有效性与实用性。