对3种典型检波器及其数据的几点看法

魏继东

(中石化石油工程地球物理有限公司胜利分公司,山东东营 257100)

动圈式速度检波器与水中压电检波器分别是当前陆地石油勘探与海洋石油勘探最重要的采集设备,二者基于不同的物理原理,目的都是将由震源激发的地震波场(弹性波、声波)表达为可以计算、分析的数据,进而反演地下介质的空间和物性特征,确定油气藏等地下矿藏的分布范围、地质储量、开采难度等要素,为其后的油气田开发指明方向。压电陶瓷作为水中压电检波器普遍采用的机电转换材料,采用不同于水中压电检波器的外形、数量并与质量块结合(此时压电陶瓷既作为机电转换元件,又作为类似于弹簧的弹性元件),得到的输出电压在一定频带内与输入振动的加速度成正比,可被用于陆地地表振动的检测,被称为“陆地压电检波器”。

动圈式检波器、水中压电检波器和陆地压电检波器具有各自不同的物理结构、力学模型、等效电路以及传输函数,充分理解3种检波器输出数据的物理意涵以及数据意义,对于确保后续处理方法的物理合理性以及数学有效性具有重要意义。其中,动圈式检波器与陆地压电式检波器可以用弹簧-质量块-阻尼(k-m-c)单自由度振动模型进行描述,主要利用弹簧质量系统的强迫振动特性来进行振动测量,属于惯性式检波器。当前部分文献[1-3]主要关注不同类型检波器的机电构成以及传输函数的推导与表达,对于不同类型检波器输出的数据的地球物理意义论述较少。本文意图在厘清不同类型检波器机电构成以及传输函数等数理特征的基础上,检视部分与检波器类型有关的数据计算过程的物理合理性,初步探讨不同类型检波器数据对后续处理成果信噪比、分辨率等的影响。

1 3种检波器的物理结构与数学模型

1.1 动圈式检波器

动圈式检波器是在用检波器类型中历史最为悠久的石油勘探用检波器[4]。动圈式检波器输出的电压与地表振动速度在主要频带内成正比,所以被称为“速度型”检波器,其物理结构、等效电路、传输函数等见表1[5]。动圈式检波器的系统特性既取决于质量块的重量、弹簧的弹性系数,也取决于线圈磁通、磁电转换系数等电磁参数。所以,动圈式检波器在地震勘探有效频带内的系统特性(自然频率、阻尼等)取决于“材料、外形、电、磁”等多种因素(表1)。

1.2 水中压电检波器

当沿着一定方向对某些电介质施力使之变形时,介质内部会产生极化现象,同时在它的两个表面产生符号相反的电荷(作用力方向改变时,电荷的极性也随之改变)。去除外力后,电介质又会恢复不带电的状态,这种现象称为压电效应。具有压电效应的物质很多,如天然石英晶体、人工制造的压电陶瓷、锆钛酸铅等。水中压电检波器即是根据压电陶瓷元件的压电效应制造的传感器[5-6]。

水中压电检波器(水检)的自然频率取决于压电片的物性以及外形,通常非常高,可以达104Hz甚至更高的量级,所以海洋勘探时水检在远低于其自然频率以下的频带工作[6]。在实际应用中,由于压电陶瓷元件具有很高的输出阻抗,而地震仪的输入阻抗低得多,所以长期以来广泛使用变压器耦合进行阻抗匹配,被称为“变压器耦合式压电检波器”[5]。为了减少导线间的漏电作用,变压器一般靠近压电陶瓷元件。在单独的水中检波器中,变压器通常置于检波器内,而拖缆通常是一道检波器组合共用一个变压器。水中压电检波器的物理结构、等效电路等参见表1[5]。因为压电陶瓷本身的自然频率远高于地震勘探的有效频带,所以影响水中压电系统特性的主要因素是变压器以及分流电阻,其作用可用LCR振荡电路进行描述,后者具有高通滤波的作用。需要说明的是,这种高通滤波特性由附加电路带来,与压电陶瓷的自然频率关系不大。另外一种水检为“带电荷放大器的压电检波器”,利用电荷放大器来提供低输出阻抗,并对压电检波器产生的信号进行放大[5]。

因为附加电路的存在,水中压电检波器同样存在类似动圈式检波器的自然频率、阻尼等概念,在自然频率以下以一定的速率衰减。但是,这种衰减是由纯电路因素导致的,与动圈式检波器“机械+电磁”因素导致的低频衰减不同。水中压电检波器通常采用与动圈式检波器大致相同的自然频率(如10,15Hz)以及阻尼系数(比如0.707),这一点为双检合并技术的应用提供了便利(具有相同的高通滤波效应)。

1.3 陆地压电检波器

基于压电材料的压电效应,20世纪60至70年代美国有公司采用压电陶瓷作为机电转换元件,在多个压电陶瓷片上附加一个质量块(表1),当检波器振动时,质量块对压电晶体产生压力,从而在压电晶体两端产生电压,将地表振动转换为电信号。近年来国内公司在该设计基础上进行了改良,生产了多款陆地压电检波器[7-9]。较美国公司产品而言,国内陆地压电检波器没有“积分放大电路”,所以前者是速度型检波器,后者是加速度型检波器。

陆地压电检波器受压电材料机电转换系数的限制,产生的电信号比较微弱,必须通过放大器进行放大后才能被地震仪接收,所以陆地压电检波器采用了变压器设计,以实现与地震仪的阻抗匹配以及信号放大,但是这种设计带来了额外的电噪声,缩小了地震数据的有效动态范围。

陆地压电检波器准确的传输函数未见诸于文献(表1),从实际数据来看,陆地压电检波器存在与动圈式检波器类似的高通滤波作用。

由表1可见,动圈式检波器是“速度型”检波器,其输出数据在一定频带内与地表振动的速度呈线性关系;水中压电检波器是“压力型”检波器,其输出数据在一定频带内与周围介质的压力成正比;陆地压电检波器是“加速度型”检波器,其输出数据与地表振动的加速度在一定频带内成正比(不加积分电路的情况下)。

2 动圈式检波器与陆地压电检波器对地表振动的等效表征

检波器的主要功能是“忠实地记录大地振动”。对于振动表征而言,如果不考虑振动的直流分量,位移、速度、加速度是等效的。但是,因为目前无法直接测量机械振动,必须经由机电转换和模数转换等,才能实现机械振动的位移、速度或者加速度表达,这样会不可避免地产生系统噪声(机械、电磁、数学),如本底噪声会对地震数据高低频两端的保真度产生影响。但是,对于成熟的工业用检波器而言,地震信号的主要频段都是可靠的[10-11]。

图1对比了3种检波器(相距20cm)的振幅谱。由图1可见,陆地压电检波器(LP)的振幅谱(蓝色)与动圈式5Hz检波器的振幅谱(绿色)在主要频带内具有高度一致性。红色振幅谱来自Sercel公司生产的DSU3检波器,因为理论上该检波器的振幅谱没有低频衰减,所以低频较动圈式5Hz检波器以及陆地压电检波器更强,理论测试结果与实际结果相符。此外,动圈式5Hz检波器经过检波器反褶积[12]后,低频端与DSU3检波器的振幅谱高度一致。陆地压电检波器的低频衰减无明确的公式表示,故无法通过确定性反褶积进行低频补偿。

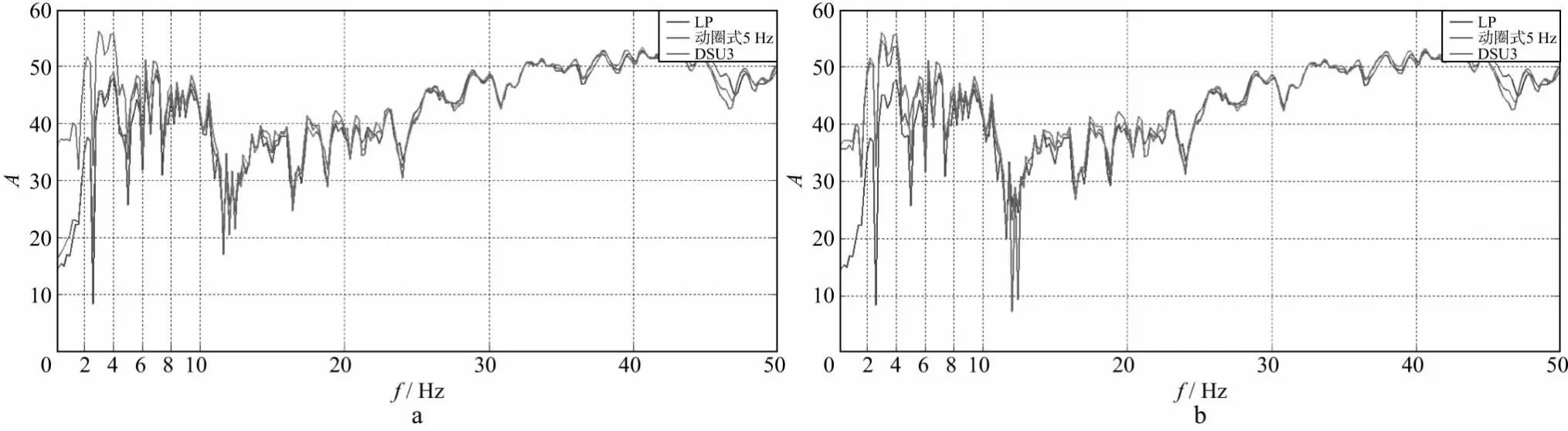
图1 3种类型检波器就近(20cm)放置时地震数据反褶积前(a)、后(b)的振幅谱

为了测试图1中动圈式5Hz检波器、陆地压电(LP)检波器的一致性,对其进行了微型盒子波试验[13],将两种检波器分别选用16个并记录单炮记录(图2)。由图2可知,尽管输入信号强度逐渐降低(初至-中深层-深层-环境噪声),但动圈式5Hz检波器的输出数据始终保持了极高的一致性。并且,因为该数据经20～80Hz滤波处理(远离动圈式5Hz检波器的低频滤波效应范围),所以认为动圈式5Hz检波器所接收到的地震波形是可靠的。与此同时,LP检波器(第2道反道)在信号最强(初至)时与5Hz检波器之间的一致性较高,其自身16个检波器相互间的一致性也较高。但是,随着输入信号强度的下降,16个陆地压电检波器相互间的一致性及其与5Hz检波器之间的一致性逐渐降低。在输入信号一致的情况下,这种不一致性是由于检波器自身机电性能(比如本底噪声高、陶瓷片一致性差)以及更大的外形与重量带来更强的耦合效应导致的。这种不一致性在一定程度上会掩盖有效信号,降低地震数据对弱信号的表达能力。对于地震数据处理来说,这种由检波器导致的不一致性会被误认为是地下介质的不一致性导致的,进而导致数据假象。

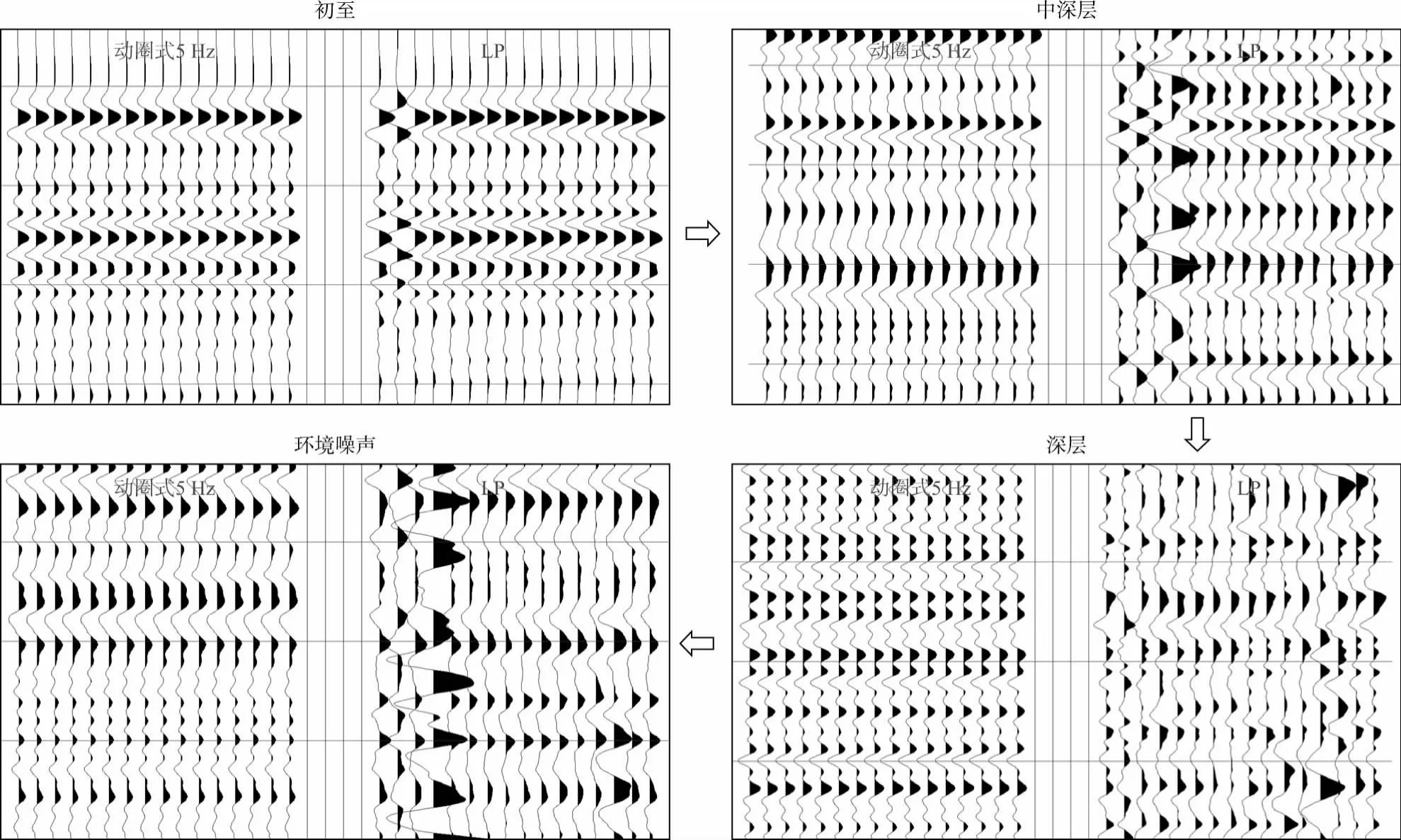
图2 各16个动圈式5Hz检波器和陆地压电(LP)检波器的单炮记录对比

3 双检合并消除鸣震干扰

自1989年BARR等[14]提出通过双检合并消除水层鸣震干扰和具有工业应用意义的海底电缆设计以来,双检(水检、陆检)数据采集、处理技术得到了长足的发展,很多学者从不同角度提出了各种压制水中鸣震(water column reverberation)的方法[15-17]。该技术的基本理论依据如下:对上行波而言,水、陆检接收到的子波极性相同、下行波极性相反,二者合并后,可以衰减除一次波以外、在海水自由表面与海底之间往返传播的多次波(图3a)。对水陆检数据进行适当的运算[16,18],可以实现上、下波场分离(图3b)。水、陆检接收到的上行波极性相同而下行波极性相反,是因为两类检波器拾取压力、速度两个物理量并表达为电压的物理机制不同。陆检是感受速度的检波器(MEMS检波器感受加速度需要将数据积分并切除1～2Hz以下的低频),其输出电压在一定频带内与水体质点的速度成正比。水检是感受压力的检波器,其输出电压在一定频带内与压力成正比。同时,水、陆检输出数据的正、负号也有着不同的物理含义。对陆检而言,其数据的正、负号分别代表质点速度的不同方向;对水检而言,其正、负号代表水体的膨胀与压缩,质点速度的上、下以及水体的胀、缩首先经机电转换表现为电压的正、负,然后再经模数转换表现为数字的正、负。按照惯例,速度向下为正、向上为负,水体的膨胀为正、压缩为负。当然这种惯例是人为设定、约定俗成的,便于更改[19]。

图3 双检合并消除鸣震(a)、上下波场分离(b)以及动圈式速度微分后与水检的波形比较(c)

地震“波场”如果用压力或者速度来表征的话,因其代表作用是一样的,故二者可以相互推算。但是,因为实践中检波器只能放置在三维空间中的某些点(理想化的质点)上,并且上行波与下行波相互混叠,所以无法对单个检波器的数据直接进行压力与速度之间的相互推算。根据地震波动力学的相关原理,必须将同一类检波器布置在不同的空间位置,加入空间参量,或者在同一个空间位置上同时布置压力和速度检波器,才能实现地震波场在该空间位置上的完整表达[20-21]。

水陆检数据表征上行波极性相同而下行波极性相反,本质上是单一类型检波器对波场表征的不完备导致的,这一点恰恰为双检合并、波场分离提供了可能(图3a、图3b)。

由文献[14,19]可知,我们可以基于以下假设,利用双检合并技术压制鸣震干扰。

3.1 地震波场是平面波场

在平面波场的假设下,由波动方程、牛顿第二定律以及胡克定律可以推知地震波场中的压力与速度存在以下关系[14,22-25](假设一维):

(1)

式中:P为压力,单位Pa;ρ为水体密度,单位kg/m3;c为水体速度,单位m/s;v为水体质点的振动速度,单位m/s。

由(1)式可见,理想化情况下,将水检检测到的压力P与被标定后的陆检数据ρcv相加,上行波得到加强(2P),下行波得到抵消(-ρcv+ρcv=0),这是双检合并消除鸣震干扰的基本原理。部分文献[4,26-28]将水中压力型检波器等同于加速度型检波器,缘于对水检所应用的牛顿第二定律的误解,认为水中压力型检波器拾取的是“力”信号,所以根据牛顿第二定律:

f=ma

(2)

式中:f为压力,单位N;m为水检的质量,单位kg;a为水检的加速度,单位m/s2,可以推断水检输出的数据正比于加速度。但是就水检的工作原理而言,水检输出电信号与水检周围水体的“压力”(更准确而言是压强)而不是“力”成正比,“压力”的单位为Pa(根据相应灵敏度换算后),“力”的单位为N。水检适用于牛顿第二定律的形式为(假设一维):

(3)

式中:t为时间,单位s;z为距离,单位m。

(3)式表达的是水体在无检波器情况下质点振动速度v与压力P的关系。在介入检波器的情况下,水体与检波器之间产生了耦合效应,主要影响信号高频端的保真度[29-30]。

因此,认为水检等同于加速度检波器、应该将速度型动圈式陆检微分为加速度后再与水检进行合并的做法不符合地震波动力学原理,在此基础上发展的数学去鸣震方法缺乏物理合理性。将速度检波器微分为加速度后,子波波形会发生改变(图3c),无论如何选择标量标定算子,都很难将鸣震干扰的速度和压力分量抵消,并且会形成新的干扰波。因此,尽管对野外实际而言,很多陆检记录的主频低于水检主频,但是这种差异并不是两种检波器跟踪物理量(速度/压力)不同导致的。将单个地震子波表达为速度或者压力并不会导致主频上的差异,导致主频差异另有原因。

平面波场是双检合并消除水层鸣震的物理前提。在地震波场远离震源或者反射面时,可以将地震波近似为平面波场[31]。但是,对于OBC/OBN技术来说,检波器恰恰位于反射面附近,所以其速度与压力关系是否符合(1)式,进而使得双检合并取得理想效果,缺乏足够的理论与实践证明。目前,没有文献记载在现实中测量到速度与压力在这种微观(海底与电缆之间的距离)、临界(入射波与反射波、透射波同时对检波器产生影响)、大尺度(电缆的长度与视波长的量级相当甚至更大)条件下的理想关系。

3.2 检波器距离海底非常近

由文献[14]可知,在海底水固界面法向应力、位移连续且切应力消失的情况下,其平面弹性波的解析解如图4a所示。在该文献中,假设检波器位于水中且距离海底非常近(远远小于地震波长)但又不与海底接触,这样就可以忽略海底入射波A1、海底反射纵波A2以及反射横波B2的影响,而只考虑透射纵波A′1(图4b的t1)及其后续引发的在水体中往复传播的鸣震干扰(图4b的t2,t3,…)。在这种假设条件下,可以将由海面下行的海底入射波(鬼波,ghost)与由海底上行的反射波(微屈多次波,Peg-leg)时差视为0(此处定义入、反射波的标准是基于置于海底检波器),即几乎同时发生。比如,对于压力波场而言,海底入射(-1)和海底反射(-Kr)同时发生在t2时刻,且二者之间的关系符合反射定律(图4a)。在这种理想情况下,经过适当标定后可以消除除一次波以外的由海水自由表面反射到海底的干扰波(ghost)以及由海底反射回海面的波(peg-leg)[20,30,32],而不是仅仅衰减下行波[24,33]。之所以可以达到这样的目的,是因为海底入射波的振幅要大于反射波的振幅(1>Kr),在二者反相时,极性取决于入射波,在二者同相时,极性仍然取决于入射波。所以二者叠加后的子波极性取决于入射波(即下行波),而水陆检的下行波极性相反。

图4 地震波在海底的分裂(a)与双检合并消除鸣震的时域算子(b)

3.3 不考虑与海底以及海水的藕合效应

在海底介质非常软、横波速度很小的情况下,海底与检波器之间的耦合效应对地震数据的影响非常大,难以忽视[34-38]。文献[35]认为海底电缆垂直方向z与in-line方向x与海底耦合得较好,cross-line方向y耦合得较差。由于OBC外形的限制,其长度(千米级)大于地震波长(十米级-百米级),所以无法用单自由度振动系统对其进行数学描述,电缆与海底之间的耦合关系尚不能用明确的数学模型表示。并且,因为海底电缆位于海床之上,并非完全直线,同时地表起伏等导致耦合情况变化较大,所以很难将陆检的in-line方向x输出等同于海底的x方向振动。

海底节点仪(OBN)的外形更小、较横波波长(与耦合效果密切相关)更接近于“质点”的假设。海底节点仪同时与海底和海水接触,其传输函数[37-38]较陆地[39-40]更为复杂。

文献[14]和文献[19]提出采用标量算子来校正水陆检之间的数据差异。但是由于耦合等原因的影响,一个标量算子并不能完全代表水陆检之间的数据差异。文献[36]采用依赖于频率的算子来校正二者之间的差异,取得了较好的效果。

如果检波器中立地漂浮于水体中(即平均密度与水体相当)且非常接近海底,尽管仍然存在与海水耦合,会对高频振动产生衰减[30],但更满足文献[14]所假设的条件。不过这样又会导致横波无法正常接收。

3.4 不考虑检波系统的机电效应

图4仅从理想的地震波动力学的角度考虑了波场在海底的分裂与传播,除了与海底、海水的耦合因素以外,没有考虑检波器在拾取地震波(弹性波、声波)时的机电效应。文献[30]和文献[41]提到导致检波器效应的主要因素是不依赖于频率的标量——灵敏度,理由并不充分。灵敏度是标量,由此导致的差异很容易处理,双检地震检波系统涉及的机电因素并不仅仅包括机电转换系数(灵敏度)这一单一因素(表1)。不同水陆检的自然频率、阻尼系数、允差以及地震仪的本底噪声等都会对双检合并的效果产生影响。

文献[42]和文献[43]中水陆检数据的能量差异是跟踪物理量、灵敏度、记录格式差异导致的,并不意味着压力代表的地震波机械能与振动速度所代表的机械能存在极大差异。当然,水检对横波波场没有响应,陆检可以接收横波、Scholte波等,它们所表征的物理能量存在差异,但应该在同一个量级。

4 检波器对地表振动的记录与改造

检波器的功能是在震源激发地震子波后,忠实地记录大地产生的振动。因此,检波器输出数据应该“忠于”大地振动本身。除了检波器以及地震仪本底噪声、机电转换、藕合效应等因素使得地震数据较地表振动存在较大畸变以外,还存在若干环节会影响地表振动的准确表达。

4.1 动圈式检波器的高通滤波效应

由前面的分析可知,地表振动转换为动圈式检波器质量块相对振动的过程中,会产生低频衰减(-12dB/Oct)。只要衰减后的低频信号高于本底噪声,这种低频衰减就可以通过确定性反褶积来恢复,在一定程度上再现地表振动的低频特征,代表了“更真实的地表振动”[12](图1b)。

4.2 加速度域处理地震数据

目前陆上石油勘探中主要存在速度型、加速度型两类检波器。其中,MEMS检波器、陆地压电检波器及涡流检波器在主要频带内与地表加速度成正比。由于自20世纪30年代以来动圈式速度检波器一直占据主导地位,很多处理软件默认输入数据为速度或者其线性等价数据,所以国内外多数油气勘探公司将加速度数据积分为速度、切除低频后再进行处理[44-47],以便保持后续有关计算的物理合理性。

比如,已知平面S质点振动速度法向分量振动速度为vn的情况下,可以利用瑞雷积分[48]求取任意一点A的频域压力波场PA:

(4)

式中:j为虚数;ω为圆频率;r为A点到S平面上某点的距离;vn为平面S上质点的法向振动速度;ρ为密度;Kr为波数。

如果将加速度检波器采集数据直接输入处理系统,求取的值与该点压力场的微分成正比(比例系数决定于检波器灵敏度等检波系统因素),不代表该点的压力波场。此外,分别用速度和加速度表征地震子波,因为由波前扩散和大地吸收引起的振幅衰减速率不同[49],所以速度、加速度的动力学特征(频率、振幅、相位)存在较大差异,如果不将加速度数据积分为速度而直接输入处理系统的话,处理后的剖面视觉分辨率看似增加了(同相轴更多),但是实际地震分辨率、特别是深层的分辨率与信噪比会降低,同时会产生相位错动,进而影响解释精度。

4.3 经电路频谱整形或者微分

文献[50]至文献[55]主张在野外利用电路提高地震仪模数转换之前高频端的电压值,或通过电路将速度信号微分为加速度信号,或采用加速度检波器接收,以期提高高频信号的“可记录性”进而提高分辨率。以上野外电路提频、整形、微分或者直接利用加速度检波器接收理论上存在两个优势:①使高频端信号远离本底噪声,机电比[12]更高;这就使得原先部分低于本底噪声的高频信号得以高出本底噪声从而被更准确地计入二进制数字,为后续利用数学方法提取高频信号预留了可能性;②在一定程度上弥补大地滤波效应带来的高频损失。

但是,以上措施也存在明显的不足:①高频端的地震信号很弱、环境噪声很强,所以即使提升了高频端的机电比[11-12],如果不能有效衰减高频端的机械噪声,就很难将野外提频的优势显现出来,甚至会降低信噪比;②野外提频在一定程度上可以补偿大地吸收衰减作用,但是这种补偿相较实际的大地吸收而言,远远不够。野外提频或整形是由电路实现的,一旦设定后就难以改动、不够灵活。在保证机电比的情况下,完全可以通过后续数学方法,如反Q滤波进行提频,去噪后提频的效果会更好。

所以,检波器只要在多次覆盖背景下在主要频段(1～200Hz)[11]保证一定的机电比(比如>10),就可以通过数学方法保真地恢复其所表征的地表振动(位移/速度/加速度)。在检波器灵敏度合理(如无源速度检波器80～120V/m/s)、地震仪或者节点仪采用24位AD转换(有效动态范围>120dB)的情况下,不必采用野外提频、频谱整形或者微分的处理方式来“提高高频信号的可记录性”。如果在野外进行了以上改造,也应该在室内用数学方法将电增益去掉。

所以,检波器只要能够最大限度保真地记录大地振动就是合格的检波器,经过电路频谱整形[53]、“截频当做通频用”(高低截+高增益)[52]、“兵分两路”(高低频分开记录)[55]以及将速度检波器输出经电路微分[56]再进行模数转换的做法,在提高高频端机电比的同时,降低了低频端、特别是极低频端的机电比,同时对检波器接收到的、默认为速度量纲的波形进行了较大改造、不再线性于地表振动的速度表达。如果后期没有通过数学方法消除电增益,会将信噪比更低的高频端反应到时域波形,使得子波旁瓣增加,降低分辨率和信噪比,因为“信噪比的提高最终体现在时域”[57]。

5 检波器的分类

从检波器输出电压与被检测地表振动之间的关系来看,检波器通常包括位移型、速度型、加速度型3类。但是,类型的划分可以更详细地分为两种情况:基于“质-弹-阻模型”的单自由度振动系统中“质量块相对位移与地表振动”的关系,以及地震检波系统中“输出电压与地表振动”之间的机电转换关系。前者可以简称为基于“机-机转换”(分类Ⅰ),后者简称为“机-电转换”(分类Ⅱ)。两种分类系统下,3种类型检波器分别具有不同的定义[1-2](图5)。

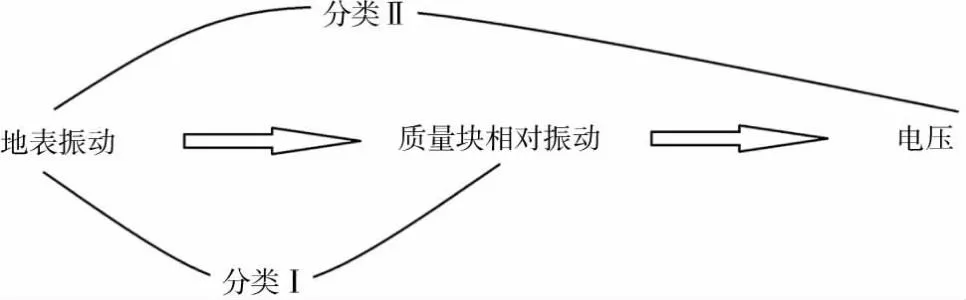
图5 两种检波器分类系统的对比[1-2]

根据单自由度振动系统的特点,当被测频率远大于系统自然频率的时候,质量块的相对位移Dm与大地振动的位移Dg成正比,该检波器称为位移型检波器;当被测频率与系统自然频率接近的时候,Dm与Dg的一次微分(速度)成正比,该检波器称为速度检波器;当被测频率远小于系统自然频率的时候,Dm与Dg的二次微分(加速度)成正比,该检波器称为加速度检波器。假设系统的自然频率为f0,加速度检波器、速度检波器、位移检波器各自的工作频段见图6a。也就是说,这种分类某种意义上取决于被测频带与系统自然频率的相对关系。如果系统的自然频率是60Hz,而被测频段是1～10Hz,那么这种检波器可以称为加速度检波器;如果被测频带在60Hz附近,可近似称为速度检波器,如果被测频带为100～200Hz,该检波器为位移型检波器。也就是说,对于同一个检波器而言,其类型是由被测频带决定的。

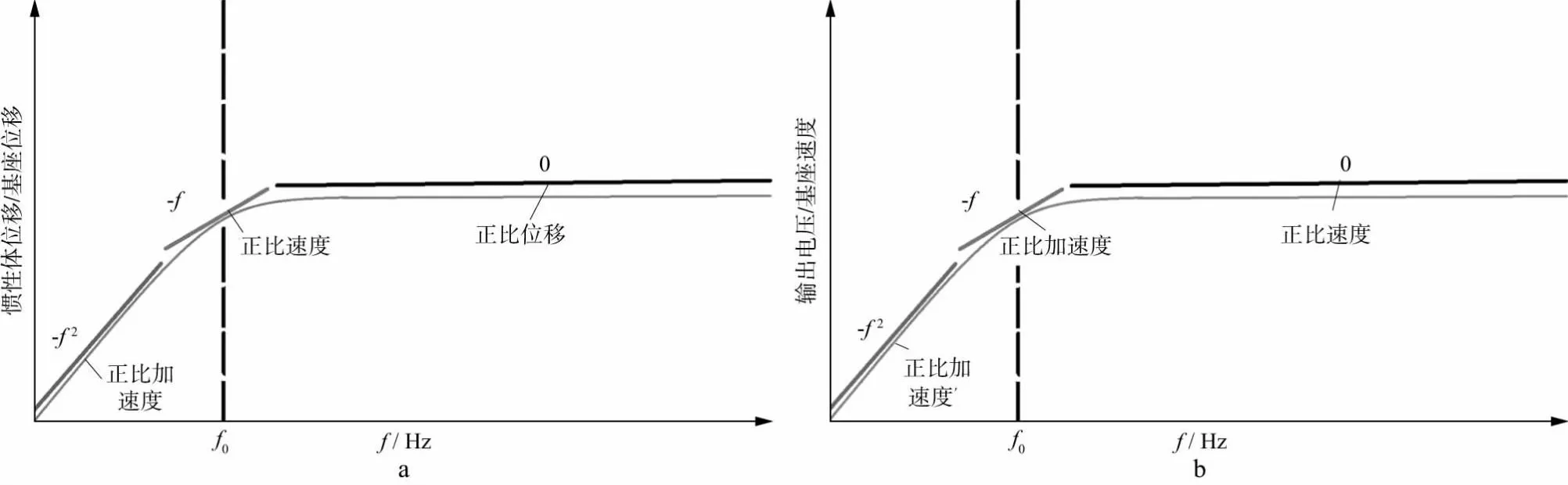
图6 检波器分类Ⅰ(a)与分类Ⅱ(b)在频域的差异

分类Ⅱ取决于检波器输出电压与地表振动之间的关系。如果在主要测量频带内输出电压分别与地表振动的位移、速度、加速度成正比,则分别被称为位移型、速度型、加速度型检波器。

因为陆上石油勘探通常的有效频带在1～200Hz[11],如果动圈式检波器自然频率为10Hz,其接收到的信号由低到高的频段分别包含了速度的二阶微分、一阶微分(加速度)以及速度等不同物理量纲组成的复合信号,并不是单纯的速度信号(图6b)。特别地,当目的层较深、反射信号主频较低时(如1～20Hz),速度的一阶、二阶微分所占比例很大,信号被改造的程度更大,不再是“纯粹的速度信号”,低频信号被人为地衰减了,这种构成对于低频勘探不利,需要通过检波器反褶积[12]将自然频率附近以及以下的频带校正为速度信号(图1b)。

通常情况下,惯性检波器质量块的相对振动只有被转换为电压后才能经模数转换转化为可施加运算的数据,所以分类Ⅱ更具概括性,也更容易理解。因此工程层面上多采用分类Ⅱ进行分类。

6 结束语

1) 动圈式检波器与陆地压电检波器在主要频带内对地表振动具有等效的表征作用。后者因为材质、工艺、成本等原因,一致性稍差。

2) 传统的OBC、OBN双检合并消除鸣震技术所设定的前提,如地震波场是平面波场、与海底距离非常近但不接触,不考虑耦合效应、不考虑检波系统的机电效应等,与施工实践存在一定差异,尚需深入的针对性研究与试验并应采取相应的工程措施,以提高该技术的应用效果。

3) 借助野外电路提高高频端机电比或者采用加速度接收对于提高地震数据信噪比以及分辨率并无太大帮助甚至会带来更多的噪声,进而增加后期去噪的难度;在处理软件默认输入数据为速度的情况下,频谱整形后的数据应采用数学方法去除电增益,加速度检波器接收的数据应先转换为速度再进行处理。