生成式对抗神经网络的改进及其在地震数据压噪中的应用

彭海龙,李 明,孙文钊,李 列,周 凡,鲁统祥,江 凡

(中海石油(中国)有限公司湛江分公司,广东湛江524057)

地震数据在采集和处理过程中受随机噪声的影响,造成地震数据品质的降低,进而影响后续地震解释工作对地质信息的解读,不利于目标圈闭和油气藏的评价[1]。为此,地震数据处理需要一种能够高效率高质量压制地震随机噪声的技术,以提高油气勘探成功率,这也是当前地震数据处理技术的终极目标。随着计算机技术的发展,深度学习技术已经得到广泛应用,并在地震数据处理中发挥了重要作用。

目前地震随机噪声去除方法主要有两大类。一类是根据信号与噪声差异性特征进行去噪的传统方法,主要包括各种变换域去噪方法和时-空域去噪方法[2],如双边滤波[3]、高斯滤波[4]、三维块匹配滤波算法[5](block-matching and 3D filter,BM3D)、加权偏振滤波[6]、曲波变换去噪算法[7]等。上述算法具有良好的去噪效果,但是计算效率相对低,对地震数据的边缘细节保护性差。另外一类是基于深度学习的去噪方法,此类方法根据地震数据有效信号与噪声的特征差异进行地震数据的去噪[8]。早期深度学习方法在进行地震数据去噪时,主要是基于前馈神经网络以及多层感知器开展处理工作[9],对地震数据的构造信息及边缘细节信息具有较好的识别及检测能力,在地震数据去噪过程中能够发挥一定的作用。但是常规深度学习算法大多采用判别模型来模拟噪声模型,并且需要对其进行监督。因此,GOODFELLOW等[10]在2014年首次提出生成对抗神经网络架构(generative adversarial networks,GAN),被称为是“近二十年来机器学习领域中最酷的想法”。但是利用该神经网络开展地震数据去噪时存在梯度消失和对地震数据的边缘等细节信息保护不到位等问题。2016年,U-net卷积神经网络被首次提出,相比较而言,U-net神经网络应用范围广泛,使用拼接式的跳跃连接,可以有效实现特征融合[11],但是该神经网络结构主要采用二维卷积算法,未充分利用地震数据的三维信息,因此,在实际应用中存在训练速度慢、处理效果不够理想的不足。随后RADFORD等[12]提出了基于深度卷积生成对抗神经网络的无监督表征学习神经网络(deep convolutional generative adversarial networks,DCGAN),该神经网络结构稳定,但有效信息未能得到较好的保护,且随着地震噪声等级的提升,其去噪能力下降明显。ARJOVSKY等[13]提出了一种基于Wasserstein距离的生成对抗神经网络(wasserstein generative adversarial networks,WGAN),该神经网络可以开展盲去噪,但是需要Lipschitz-1条件约束。2019年,CHEN等[14]采用广义损失感知对抗神经网络(generalized loss sensitive generative adversarial networks,GLS-GAN)进行盲去噪,通过估计输入数据的噪声分布,实现数据的盲去噪,该神经网络算法需要设置不同的损失函数,因此对于噪声类型和强度存在限制。

在地震数据处理方面,深度学习应用的最大挑战之一就是需要大量带注释的训练样本来支持推断,但地震数据往往是数量有限的注释样本,现有的地震数据在表征地下信息时存在很大的不确定性,因此很难进行可概括的特征模式学习[15]。为解决上述问题,常用方法就是通过随机的理论地质构造模型正演得到大量无噪声干扰的地震正演数据,对正演结果进行各种简单修改实现数据扩充,如坐标旋转的方式[16],该方式能够对地震信号样本的有效边缘信息进行修改,由于未引入新的地震信息,故能够获得大量不含噪声的正演模型数据,但是难以模拟得到真实的地质构造地震信息,所以存在过度拟合的问题。为应对这一挑战,有学者提出了基于实际地震数据生成复杂类型数据的合成地震数据增强方法,该方法能够衍生更多的数据来填充数据集,其中的生成式对抗神经网络模型则是合成地震数据增强方法的代表[17-18],该神经网络对于地震数据分布具备很好的生成能力,能够完成端到端的生成任务,将地震数据去噪问题转为地震信息翻译问题,即给定具备统一空间特征的地震数据集,神经网络模型能够学习对应的映射函数,从而能够生成另外一种具有统一空间特征的数据集。因此生成式对抗神经网络能够很好地表现上述映射关系,生成与原始无噪数据尽可能相似的地震数据。该方法在用于地震数据去噪时,将含噪地震数据和无噪地震数据视为两种不同类型的数据,因二者都具有多层次的不同特征,故在生成式对抗神经网络的数据信息翻译原理下开展监督学习,能够使生成器学习到两种数据之间的映射关系,从而能够实现地震数据去噪的目标。该方法对于含有特定类型及强度噪声的地震数据处理效果较好,但是面对噪声种类及噪声强度多变的地震数据时存在训练不稳定、模型难收敛的问题,因此,该方法在地震数据处理时依旧存在提升空间。

为进一步提高地震数据的去噪效果,本文在上述研究成果的基础上,提出一种改进的生成式对抗神经网络建立方法,对常规生成式对抗神经网络的生成器和判别器进行优化,改进了神经网络的模型结构。同时从损失函数入手,结合对抗损失函数、结构信息损失函数等的优势,形成全新的综合性损失函数,然后利用正演模拟数据集进行神经网络训练和测试,最后利用实际地震数据进行测试验证。

1 方法理论

1.1 U-net神经网络结构

U-net神经网络模型与全卷积神经网络(full convolutional networks,FCN)的结构较为相似[19],U-net神经网络结构如图1所示。

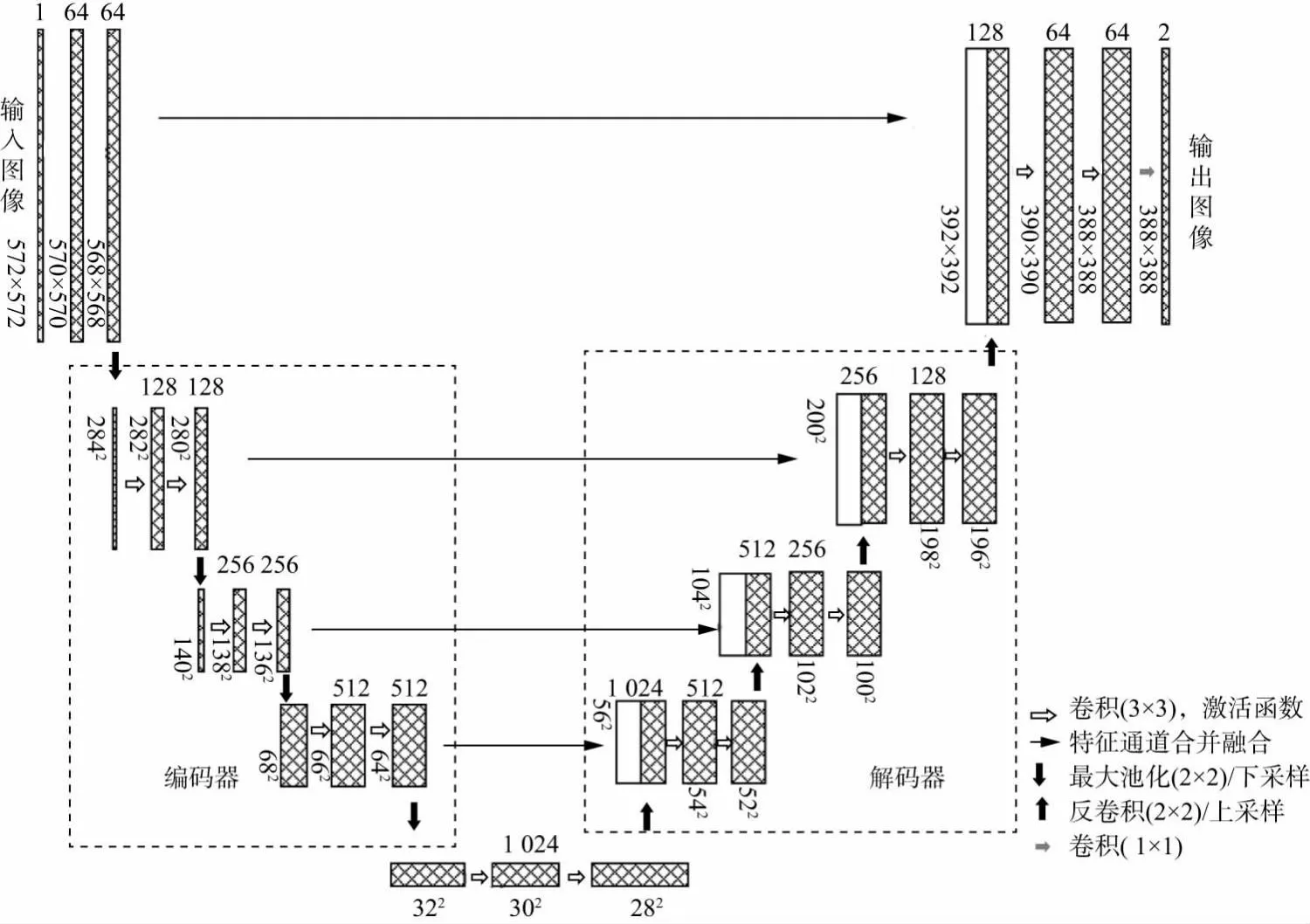
图1 U-net神经网络结构示意

U-net神经网络和FCN神经网络均含有编码器和解码器,二者都存在跳跃连接的拓扑结构[20-21]。U-net神经网络在结构形态上左右对称,其左侧神经网络结构用来捕获上、下文信息的收缩路径,右侧用于执行精确定位的扩展路径。编码器输出的数据信息经过复制裁剪之后,同对应的解码器中经过反卷积的特征图进行特征融合,融合结果作为下一层的输入进行上采样。U-net神经网络在上采样过程中需要大量的特征通道,以保证将上、下文信息传输至具有更高分辨率的层上。

1.2 神经网络模型的改进

1.2.1 基于U-net的生成器神经网络设计

利用U-net神经网络进行地震数据去噪时,由于其生成器模型深度不够,导致对地震数据特征的数据集信息提取能力不够,因此,该神经网络对噪声和有效信息的区分效果差。U-net神经网络结构中存在最大池化层,使得神经网络模型难以保留原始地震数据的复杂细节特征信息。受ReLU激活函数的影响,神经网络的梯度计算不能持续更新该神经元的权值信息,导致神经网络存在大量的冗余参数,不利于模型的进一步学习[22]。最后,U-net神经网络在批量标准化(batch normalization,BN)层的训练中引入不同批次、不同样本的特征性关系与信息,在一定程度上弱化了单一地震数据的有效信息,不利于地震数据有效信息的还原。

为解决上述问题,本次研究采用更深层次神经网络以增强对原始地震信号的特征提取和还原能力,直接对下一层级的模型和上一层级的输出结果进行卷积或者反卷积,从而避免U-net结构中上采样和下采样层丢失或者损伤地震信息,能够最大程度保持原有的地震信息的细节纹理、结构特征等多维信息。

为解决批量地震信号样本的特征关系信息对于单个地震信号的影响,剔除U-net神经网络结构中的BN层,在神经网络训练中对单个地震信号的均值和标准差进行标准化处理,以确保不同信号之间的独立性,避免批量标准化引发的信息干扰问题。

基于上述策略,改进的生成器神经网络结构如图2 所示。

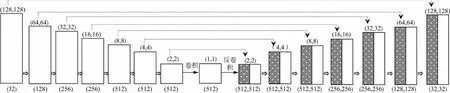
图2 改进的生成器神经网络示意

由图2可知,生成器前端的收缩神经网络中每一个模块都包含一个尺寸为4×4的卷积层和LeakyReLU激活层,其中方框顶端的数据表示特征图尺寸,方框底部的数据表示通道层数。从左到右,前4个模块用于对地震数据特征图尺寸进行缩小,由128×128逐步缩小至16×16,同时信号的通道由32层逐步扩展到256层;后3个模块将通道扩张为512层,但特征图的尺寸进一步缩小至2×2。在后端的扩张神经网络部分,全部为尺寸4×4的反卷积层和LeakyReLU激活层。每一个特征图和收缩神经网络均通过跳跃连接在通道上实现嵌合,因此该层的特征图尺寸、通道数和收缩神经网络一致。然后利用尺寸为4×4的反卷积层依次进行反卷积操作,输出与原始信号相同尺寸的信号。

1.2.2 判别器神经网络结构设计

生成器的功能是生成与无噪地震信号尽可能相似的信号,判别器则是对两个信号进行区分。因此判别器需要具备监督和对抗生成器的作用,要想实现上述目标需要判别器具有优秀的判别能力[23]。在神经网络的迭代学习中,随着两种信号之间的相似性逐渐增加,对判别器的要求也随之升高。为进一步提升U-net神经网络中判别器对生成信号和原始地震信号的判别能力,本次研究在降采样层中依次降低地震信号的尺度,让判别器从不同的尺度来分析判断地震信号,改进后的多尺度判别器神经网络结构如图3所示。

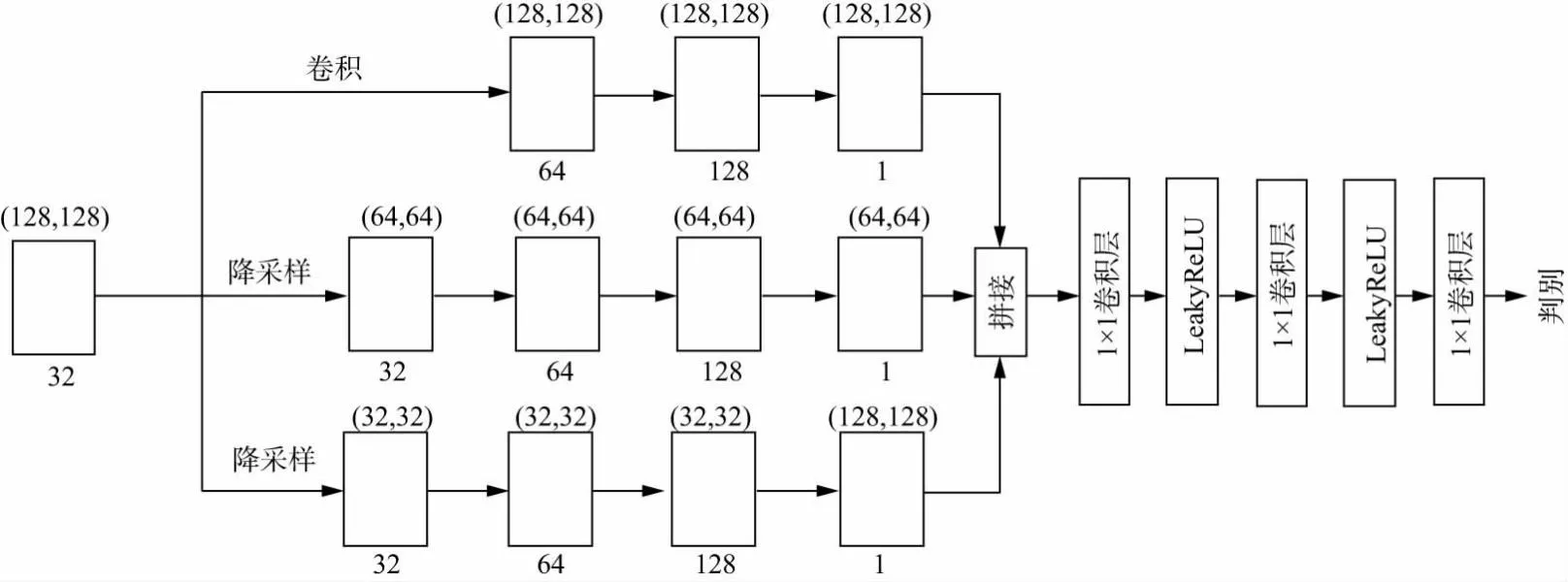
图3 改进后的多尺度判别器神经网络结构

由图3可知,在判别器神经网络结构中,存在3个不同尺度、相同结构的子神经网络。在训练过程中,首先利用第一个子神经网络判断原始尺度,然后通过降采样的方式利用后两个子神经网络,分别判别低尺度的地震信号,最终以权值叠加的方式输出结果。改进的判别器神经网络结构可以从多个角度提升生成器的性能,其中大尺度判别器有利于生成器生成与全局更为一致的地震信号,小尺度判别器有利于提升生成器对细节的生成能力。

1.2.3 改进后的神经网络模型结构

利用上述生成器和判别器,得到改进的生成式对抗神经网络模型结构如图4所示。

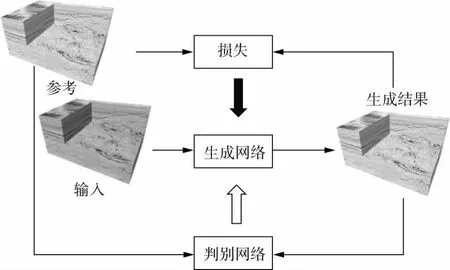
图4 改进的生成式对抗神经网络模型结构示意

1.2.4 损失函数的优化改进

U-net神经网络的损失函数只考虑了对抗损失,因此存在鲁棒性不强的缺陷[24]。其目标函数很难描述复杂地震信号对边缘细节的特征需求,导致生成式对抗神经网络难以准确描述地震信号的特征。为进一步提高对抗神经网络的性能,需要优化神经网络模型的损失函数。

1.2.4.1 对抗损失

目前常用的生成式对抗神经网络目标函数为LSGAN函数,其表达式为[25]:

(1)

(2)

式中:D表示判别器神经网络;G表示生成器神经网络;E表示期望;x表示服从真实地震信号分布的地震数据;z表示服从随机噪声分布的地震数据;a和b分别表示去噪地震数据标准和真实地震数据的标注;c表示判定为真实地震信号的标准;Pr表示真实样本数据;Pz是输入的随机样本数据。鉴于本文研究的是一种监督学习条件的生成式对抗神经网络,需要生成器生成波阻和相位等更接近真实地震数据的结果,因此需要在损失目标函数中引入原始含噪地震信号的分布数据、服从无噪地震信号分布的数据、服从随机噪声分布数据以及L1损失函数,改进后的判别器的损失函数LG和生成器损失函数La分别如(3)式和(4)式所示:

(3)

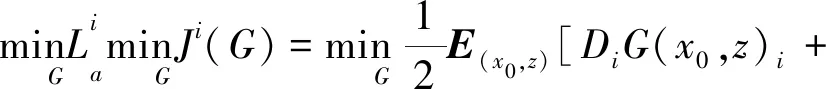
(4)

式中:i表示第i个尺度;Dk表示与其对应的判别器;xr表示服从无噪地震信号分布的地震数据;x0表示服从原始含噪地震信号分布的地震数据;ξ表示权重系数;×代表乘积。

1.2.4.2 结构信息损失

U-net神经网络执行去噪任务的最终目的就是将含噪的地震信号转化为不含噪的信息矩阵[26]。在实际数据处理中没有考虑到地震数据内部含有的地质结构信息,以往用于描述该项情形的目标函数均为L1函数或者L2函数,但是上述两种函数易存在梯度爆炸或者梯度稳定性较差的问题。因此本文引入地震结构相似度函数,建立新的结构信息损失函数。该函数根据地震数据的不同结构特征将其划分为结构规律区域和结构复杂区域,不同的区域采用不同的结构信息损失函数,两个区域的损失函数公式分别如(5)式和(6)式所示:

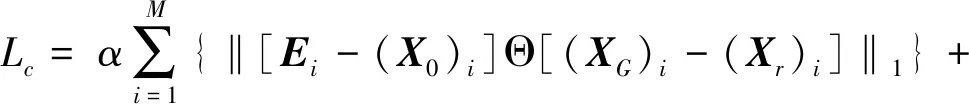
(5)

(6)

(7)

式中:Lc表示结构复杂区域的损失函数;Ls表示结构规律区域的损失函数;X0表示初始图像的构造特征信息;Θ表示Hadamard乘积;XG表示生成器生成的数据结果;Xr表示原始地震数据;S表示地震结构相似度指数;Ax,Ay分别表示两个地震数据振幅的均值;σx,σy分别表示两个数据的协方差;ai,bi分别表示不同的稳定系数;α,β表示权重系数;M表示地震信号的尺度个数。

1.2.4.3 配准损失

上述损失函数主要从神经网络结构方面入手,在生成能力和地震信号能量层面上进行神经网络训练。在实际去噪过程中,对抗损失函数不能完全约束复杂地震信号,建立的神经网络结构会带来外部噪声,从而对去噪结果产生不利影响。为得到更真实的有效地震信号,提出一种多尺度配准函数,结合多尺度判别器特征,利用多尺度不变特征变换(scale invariant feature transform,SIFT)开展特征匹配。去噪结果与无噪数据之间匹配程度越高,对应的匹配特征数目越多,特征点之间的欧式距离越小,表明去噪结果越好。利用该项匹配损失函数实现去噪数据与无噪数据之间差异的度量,可以得到准确的去噪结果,改进的目标函数表达式LF如下:

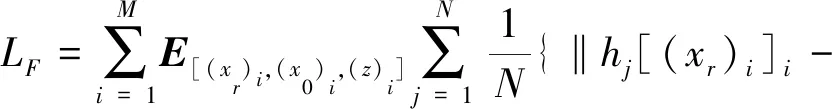
(8)

式中:N表示匹配特征数目;hj表示第j个匹配特征点的SIFT特征向量。

1.2.4.4 感知损失

利用对抗神经网络进行地震信号去噪时,需要考虑其中的地质结构细节信息,同时还要确保去噪前、后地震信号在波阻抗特征层面上的一致性。常规做法采用L2函数来约束地震信号细节的提取过程,但是该函数并不能与感知信息相匹配[27]。为解决上述不足,本文采用VGG19神经网络作为特征提取器,分别提取真实地震数据、生成数据和去噪结果的特征图,然后应用一种多尺度感知损失函数对生成器生成信号和真实信号进行感知比较,从而对信号之间的波阻抗特征进行约束,损失函数Lp表达式为:

(9)

式中:j表示第j个神经网络层;K表示神经网络层数目;Nj表示第j层整体元素数目;ωj表示第j层感知结构权重;ψr,ψG,ψde分别表示真实地震数据、生成器生成的地震数据、去噪结果数据经过VGG19神经网络的第j个池化层提取的特征图。

1.2.4.5 综合损失函数

为充分利用各项损失函数的优势,本文将上述损失函数进行综合,同时基于建立的多尺度神经网络模型,得到最终建立的损失函数为:

(10)

(11)

式中:μ1,μ2,λ,θ表示不同的约束权值。(10)式表示判别器的多尺度损失函数,(11)式表示生成器的综合损失函数。对生成器生成结果的总振幅数值大小、结构等不同层次进行约束和训练,可以有效提升生成器的去噪能力。优化器则采用自适应运动估计梯度下降(adaptive momentum,Adam)优化进行损失函数的迭代优化,通过参数空间的估计实现自适应更新步长,通过多阶矩阵修正偏差,训练鲁棒性和参数泛化性,训练过程中收敛速度快,算法流程如下。

参数:学习步长α,衰减因子β1,β2∈[0,1],目标函数f(θ),初始参数θ0,初始一阶矩估计m0←0,初始二阶矩估计v0←0,初始时间步长t←0,常数ε。

whileθt未收敛 do

t←t+1

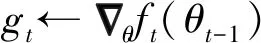
更新一阶矩估计:mt←β1·mt-1+(1-β1)·gt

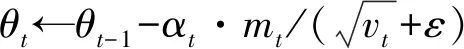
end

至此,得到本文提出的改进的神经网络训练流程(图5)。

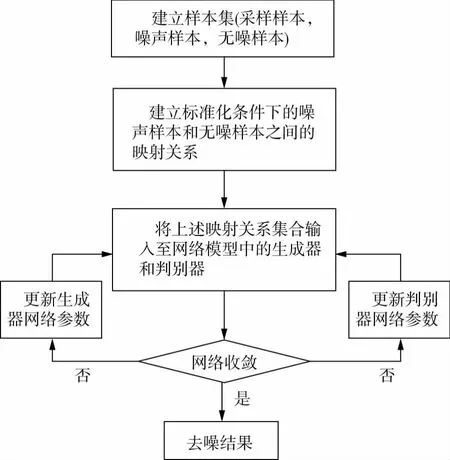
图5 改进的神经网络训练流程

2 数据测试

2.1 数据集及评价指标

2.1.1 训练与测试数据集

地震数据受采集、处理及地质情况的影响,其子波、相位、振幅及频率等信息存在较大的差异,即使同一时期采集的不同位置的地震数据也存在上述差异,因此选择样本数据时需要充分考虑上述情况充分考虑。当前较为适用的方式是通过正演方式建立无干扰地震数据,该过程参照WU等[15]提出的数据集建立思路,通过反射系数模型和子波褶积生成无噪声的正演模型数据,将此数据作为样本数据进行神经网络的学习训练。但是实际情况下,很难获取能够反映地下真实地层情况的反射系数,因此采用提取伪反射系数的方式来近似研究地下地层反射系数的分布情况,从而获取复杂程度等同于地下真实情况的反射系数。

经过大量分析可知,工区目标层位的地震主频分布范围为15～45Hz,本次研究在建立训练测试样本数据集时,设定地震子波的主频在该范围内随机变化,对应的子波选择雷克子波和俞氏子波,通过正演建立不同的训练样本,样本获取过程具体如图6 所示。构建训练样本数据集时,结合南海北部某工区地震资料的振幅、相位、信噪比和频带分布特征,确定本次训练样本集为200个。为实现三维地震数据处理,建立的样本数据和标签数据均为200×200×200的三维数据体。

图6 样本获取过程示意

2.1.2 超参数配置

模型训练之初,需要设定一些超参数,本次测试模型应用统一超参数设置,各个模型初始学习率为0.0005,先进行150轮的固定效率学习,再进行150轮的线性下降效率学习。其中,Adam优化器中,β1=0.7,β2=0.999,ε=10-1。

2.2 模型验证

2.2.1 消融实验验证

为验证本次优化的神经网络模型的各项功能,需要评价神经网络模型各模块的性能优化方式,因此采用消融模型实验对用于优化神经网络的各个模块性能进行测试。利用Marmousi模型进行消融实验,原始模型数据和含噪模型数据如图7所示。在保持神经网络模型单一优化功能程度的基础上分别计算不同实验结果的信噪比,不同程度的优化神经网络模型的消融实验指标如表1所示,不同实验结果的信噪比如表2所示。其中表1测试项1表示不做任何改进的原始U-net神经网络,将其作为生成器,对应的判别器为单一结构,损失函数也为单一对抗损失函数,测试项2是本文设计的损失函数,其它功能保持不变,测试项3则是采用本文设计的生成器和损失函数,测试项4则是采用本文设计的判别器和损失函数,测试项5则是采用本文设计的生成器、判别器和损失函数。由表2中的实验结果可知,仅具有原始对抗损失函数的模型在训练中不够稳定,难以生成有效的去噪图像。

图7 实验数据a 模型数据; b 含有高斯随机噪声的模型数据

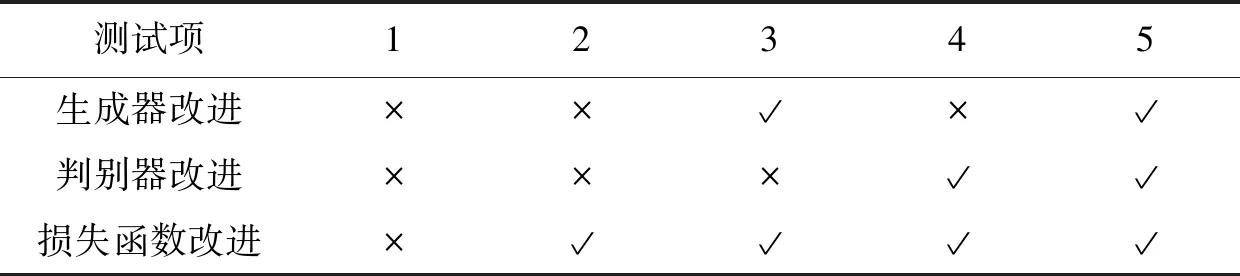
表1 消融实验指标

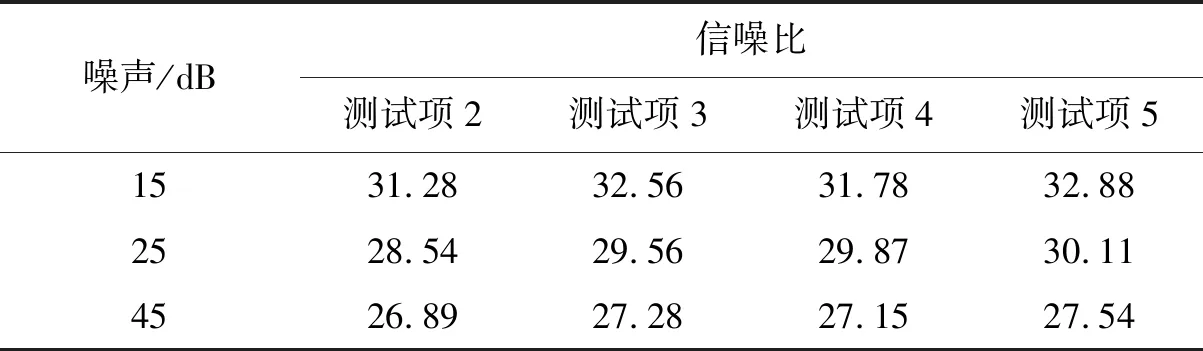
表2 不同实验结果的信噪比

2.2.2 模型数据验证

为更好地验证本文方法的有效性,在合成地震数据上添加25dB随机噪声,分别应用常规U-net、GLS-GAN方法和本文方法进行测试,对比不同方法的去噪结果。原始模型和含噪模型如图8a和图8b 所示,不同的去噪结果如图8c至图8e所示。

图8 测试模型及不同方法的去噪结果(剖面)a 原始无噪模型; b 含噪模型; c 常规U-net方法结果; d GLS-GAN方法结果; e本文方法结果

由图8可知,与含噪模型相比,不同方法去噪结果的信噪比提升明显。其中,采用常规U-net方法得到的结果相对较差,浅层的层状地层和中、深层的波状地层中存在部分“斑状”噪声。采用GLS-GAN方法得到的剖面质量较好,但是剥蚀地层顶部信息和断层区域断点和断面较为模糊。采用本文方法去噪后得到的结果在地层结构及层次性方面更清晰,断面识别度高,边缘细节效果保持更好,其去噪能力明显优于其它方法。为进一步验证本文方法的去噪能力,我们对利用不同方法去除的噪声进行对比,如图9所示。

图9 不同方法去除的噪声剖面a 常规U-net方法结果; b GLS-GAN方法结果; c 本文方法结果

由图9可以看到,利用常规U-net方法和GLS-GAN方法去除的噪声中存在部分地层有效反射信息,利用本文方法去除的噪声中地层有效反射信息最少,大部分为杂乱无规律的噪声,证实本文方法去噪能力强,对地震有效反射信息保护较好。

2.3 实际地震数据测试

为进一步验证本文方法对实际地震数据的去噪效果,利用南海北部某工区实际地震数据进行测试,该工区地质构造复杂,存在多种类型的断层,地层产状多样,且因地震采集受到相关条件的影响,地震数据中存在随机噪声,影响了地层和断层等地质结构信息的识别判断。为提升该工区地震数据的质量,采用不同方法去除噪声并进行对比,不同方法的去噪结果和去除的噪声如图10至图13所示。

图10 原始数据和不同方法的去噪结果(剖面)a 原始地震数据; b 常规U-net方法结果; c GLS-GAN方法结果; d 本文方法结果

由图10可知,3种方法去噪结果均能改善原始含噪地震剖面的质量,但是不同方法去噪结果差异明显。常规U-net神经网络的去噪结果中,地层反射同相轴边缘连续性较差,存在“锯齿”和“阶梯”状现象,部分区域甚至出现虚假断层。利用GLS-GAN方法和本文方法得到的结果相对较好,地层反射连续性好,识别能力强。利用本文方法得到的结果中地层反射同相轴连续性好,边界和断面识别效果更胜一筹,证明本文方法去噪能力优于另外两种方法的去噪能力。为进一步验证不同方法对于有效信息的保护情况,对不同方法去除的噪声剖面进行了对比,具体结果如图11 所示。

图11 不同方法去除的噪声(剖面)a 常规U-net方法去除的噪声; b GLS-GAN方法去除的噪声; c 本文方法去除的噪声

由图11可知,常规U-net方法和GLS-GAN方法去除的噪声中均不同程度地存在地层和断面的有效反射信息,GLS-GAN方法去除的噪声中有效信息相对较少。本文方法去除的噪声中,几乎看不见地层和断层的有效反射信息,表明本文方法对有效信息保护更好。为更好地展示不同方法的去噪结果,我们对比了不同去噪结果的时间切片,如图12所示。

图12 不同方法的去噪结果(时间切片)a 常规U-net方法结果; b GLS-GAN方法结果; c 本文方法结果

从图12可以看出,常规U-net方法去噪结果中,地质结构的边缘有效信息呈现“锯齿”状特征,细节不够连续光滑。GLS-GAN方法去噪结果中,部分区域存在“线性”噪声。本文方法去噪结果中地层反射的边缘信息平滑,地质结构识别清晰度高,同相轴连续性好。不同方法对地震有效信息的保护情况,如图13 所示。

图13 不同方法去除的噪声(时间切片)a 常规U-net方法去除的噪声; b GLS-GAN方法去除的噪声; c 本文方法去除的噪声

由图13可知,不同的去噪方法均能去除一定的噪声,但是去除的噪声均存在一定量的有效反射信息,表明各种方法对于地层有效反射信息均存在不同程度的损伤。相比较而言,利用本文方法去除的噪声中地层有效信息最少,证明本文方法的去噪效果最佳,对有效信息保护得最好。

3 结论

1) 针对常规生成式对抗神经网络在开展地震数据去噪中存在的去噪效果差、神经网络不稳定问题,对其中的神经网络模型结构以及损失函数进行了优化,设计了一种神经网络层次更深的生成器模型和多尺度判别器模型,从而有效提升了去噪神经网络对于地震数据细节的保护能力。

2) 经理论模型和实际地震数据验证,改进后的生成式对抗神经网络在面对复杂噪声时具备很好的去噪能力,表明本文方法对于地质结构有效信息保护较好,可以在地震数据去噪处理中推广应用。