2.5维频率域可控源电磁法水力压裂监测正演模拟

余胜红,唐新功,熊治涛

(1.“油气资源与勘探技术”教育部重点实验室(长江大学),湖北武汉430100;2.南方科技大学地球与空间科学系,广东深圳518055)

水力压裂是用于非常规油气资源开采的一项重要技术手段之一,目前已被广泛应用于煤层气和页岩气以及干热岩的开采中[1-2]。其实质是将压裂液以高压的形式注入到储层中,致使储层中原有的裂缝扩展并产生新的裂缝,从而增大储层渗透率,提高油气开采效率[3-4]。裂缝的几何形状、有效压裂体积以及扩展范围是评价水力压裂效果的主要参数。目前,微地震监测因获取信息多、操作简便等优势成为水力压裂监测最常用的方法之一[5-6]。然而,当压裂过程结束后,部分不含支撑剂的裂缝会发生闭合现象,而由于微地震监测与压裂进程的同步性,无法准确获取压裂后的有效压裂体积参数,导致对产能的预测与评价与实际情况产生偏差[7]。而水力压裂时所注入压裂液的电阻率通常比围岩电阻率低很多,电磁法具有对于地下电阻率变化反应灵敏,尤其对低阻体反应更加灵敏的优势,为电磁法用于监测水力压裂裂缝的定位和后续扩展范围评估提供了物理基础[8-9]。

目前国内外已有一些学者开展了电磁法监测水力压裂正反演的研究。YANG等[10]研究了钻孔电阻率测量中裂缝横截面积、形状及倾斜角度等参数对电磁场响应的影响,研究结果表明电磁法对裂缝的面积、形状及方位的评价具有较好的效果;李洋[11]采用有限元法实现了大型储层压裂裂缝三维空间接收响应的快速正演模拟,并模拟了甚低频(very low frequency,VLF)电磁法非对称裂缝的发育情况;KYUBO等[12]提出了一种粒子映射反演方法进行井地电磁水力压裂监测数值模拟,利用磁化率对压裂后支撑剂的分布进行了成像处理;LI等[13]将钢套管作为长电极源进行了压裂液成像的可检测性和可恢复性研究;CURCIO[14]采用几种不同的接收装置对各向异性组合模型进行了水力压裂监测试验,结果表明,电磁法监测水力压裂有助于确定裂缝的几何形状;范涛等[15]和陈理等[16]的研究结果表明,电磁数据的反演结果有助于实现对裂缝的识别和定位;由于反演多解性的问题,有学者提出将电磁法监测与微地震法联合应用的思路,以弥补各自方法的不足,提高水力压裂监测的精度[17-18]。这些关于电磁法监测水力压裂的正反演研究结果为电磁法监测水力压裂的实际应用提供了理论基础。

近年来,可控源电磁法已被逐渐应用到实际的煤层气和页岩气的水力压裂监测中。张瑞林等[19]采用瞬变电磁法监测了水力压裂时压裂液的流动方向及扩展区域,证明了瞬变电磁法用于监测水力压裂的可行性;REES等[20]采用大地电磁测深法(magnetotellurics method,MT)对页岩气储层进行了水力压裂监测,根据获取的电磁场数据,推测出了裂缝的方向和连通性;YAN等[21]采用时间域可控源电磁法(time domain electromagnetic method,TDEM)对页岩气压裂情况进行了连续监测,通过对电阻率作归一化处理分析了裂缝的空间展布形态,并与实际的钻井及地震资料相结合,验证了TDEM监测页岩水力压裂的有效性;ZHANG等[22]分析了电磁法监测评价裂缝参数的原理,通过对磁场信号的分析实现了对裂缝的长度和高度的评估;电磁法除了应用于非常规油气资源的水力压裂监测之外,也已成功应用于地热等资源的水力压裂监测中[23-24]。电磁法监测水力压裂的成功案例表明,该方法提高了对裂缝识别定位的精度,因而提高了油气资源开发的效率和产量。

时间域电磁法是目前采用电磁法进行水力压裂监测最常用的方法[25-26]。该方法采用井下激发和接收的方式获得较为精确的结果,但是方法成本高,数据处理与解释难度大,工作效率较低。可控源音频大地电磁法(controlled source audio-frequency magnetotellurics,CSAMT)是一种频率电磁测深的方法,采用接地导线或不接地线圈作为发射场源,在波区测量正交的电磁场切向分量,并计算其卡尼亚视电阻率[27]。该方法具有操作简便、工作效率高、信噪比高、探测深度深等优点,目前已广泛应用于金属矿产等资源的勘探中[28-31],而在非常规油气资源勘探开发中的应用相对较少[32-34]。实际的地质结构通常具有二维性,而CSAMT的场源具有三维性,将三维场源二维模型称作2.5维。相比于二维场源的模拟结果,2.5维的模拟结果更加符合实际地质情况[35]。CSAMT数值模拟的方法主要有积分方程法[36-37]、有限差分法[38-39]和有限元法[40-42]。相比于积分方程法和有限差分法,有限元法在模拟几何形状复杂模型方面更具有灵活性,可通过采用非结构网格精确剖分复杂的地电模型,因此在复杂结构的电磁模拟中得到了广泛应用[43-46]。本文基于2.5维CSAMT有限元正演算法开展水力压裂正演数值模拟研究,通过设计包含钢套管和裂缝的二维模型来模拟水力压裂的过程。对于数据的处理,本文采用对压裂前、后裂缝的电场响应值进行残差处理的方法,以获得压裂区域的纯异常响应,通过对纯异常响应特征的分析,阐明了采用CSAMT进行水力压裂监测的可行性。本文的研究将为CSAMT法在水力压裂监测中的应用提供理论基础,并将CSAMT法拓展到水力压裂监测的应用中。

1 2.5维CSAMT有限元法正演理论

1.1 2.5维CSAMT偏微分方程

准静态条件下电性源频率域的Maxwell方程组为(取正时谐eiωt):

(1)

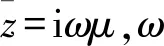
假设异常体的走向沿着y轴方向无限延伸,地下为各向同性介质,即沿着y轴方向电导率σ、磁导率μ、介电常数ε均保持不变,只在x-z平面内发生变化,电偶极子置于y轴与异常体走向平行,且偶极子中心位于坐标原点,将(1)式沿y方向作傅里叶变换后,再联立方程组即可得到波数域中其它方向电磁场分量的求解表达式:

(2)

(3)

(4)

(5)

将(2)～(5)式分别代入(1)式,可得:

(6)

(7)

1.2 2.5维CSAMT有限元求解过程

1.2.1 有限元计算方程

本文采用伽辽金(Galerkin)法,以(6)式和(7)式为基础,通过推导相应的有限元计算方程,得到节点电磁场的线性方程组:

(8)

(9)

1.2.2 单元分析

本文采用规则的矩形单元进行网格剖分,考虑到计算速度的问题,在源和观测区域网格剖分较密,在远离源和观测区域网格逐渐稀疏。本文采用4节点双线性插值单元,第e个单元的节点局部编码见图1,双线性插值单元的插值函数表达式如(10)式所示。

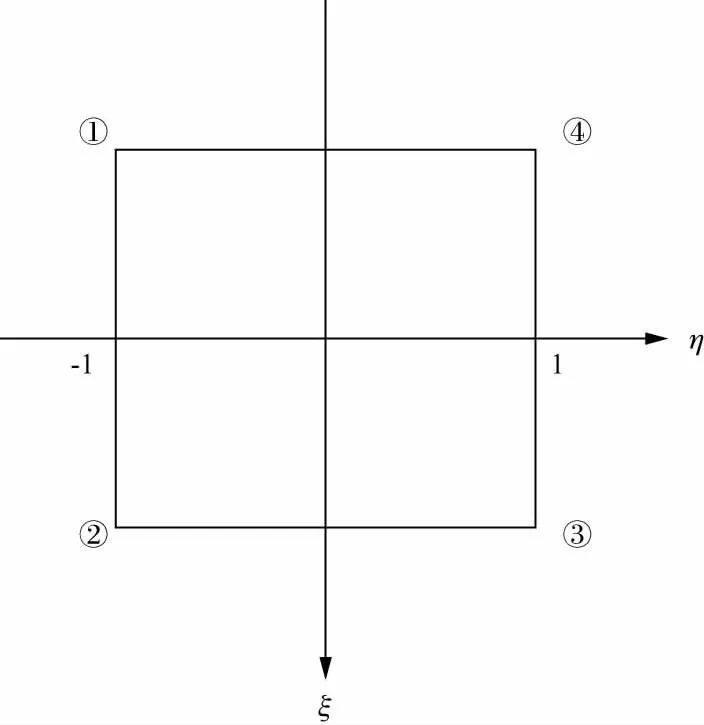
图1 双线性差值剖分单元示意

(10)

(8)式和(9)式经坐标域转换后的表达式为:

(11)

(12)

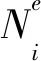
(11)式和(12)式可简化为以下形式:

(13)

其中,

(14)

(15)

(16)

(17)

1.2.3 刚度矩阵的合成

(13)式为单元e的电磁场线性方程组,可以写成如下形式:

(18)

1.2.4 场源的加载

为解决场源的奇异性问题,本文采用伪δ函数来等效场源。当伪δ函数中心位于坐标原点处时,其表达式如下[47]:

(19)

式中:r表示当电偶极子源中心位于坐标原点时,空间任意一点相对于电偶极子源点的位置;参数τ控制着发射源的规模和宽度,其值应设为场源附近网格步长的整数倍,本文取τ=10。由于本文采用4节点矩形网格,因此场源被分配到了紧邻源点附近的16个网格单元上。将(19)式的源项代入(11)式和(12)式,在等效源加载的节点处作相应的场源加载即可。

1.2.5 反傅里叶变换

(20)

式中:F(x,ky,z,ω)为被积核函数,表示波数域的电磁场分量。根据(2)式至(5)式即可求得波数域的其它电磁场结果,进而可以求得空间域的Ex和Hx。

1.2.6 波数的选取

前文对2.5维CSAMT进行有限元分析及求解过程中均在波数域内进行,要得到空间域的电磁场值还需进行傅里叶逆变换。根据傅里叶逆变换的公式可知,理论上傅里叶逆变换的积分范围为无穷大,即需要进行无穷多次的正演计算,这是无法实现的。考虑到计算精度和速度的问题,本文参照了MITSUHATA[47]选取波数的方式,令波数ky取值上限为:

(21)

式中:Δ为区域离散的最小网格步长。波数的选取个数及分布决定着反傅里叶变换的精度。在给定的取值范围内(ky≤1/Δ),波数选取的个数越多,计算精度越高,同时计算量也越大。为了兼顾计算精度和计算量,一般在每个对数等间隔内取5～10个波数,便能够保证足够的计算精度。在本文计算中,波数的取值范围为10-6～1/Δ,在每个对数间隔内取7个波数,共36个波数。

2 正演数值模拟

2.1 算法有效性验证

为了验证2.5维CSAMT正演算法的正确性和精度,首先设计了均匀半空间和一维层状介质模型进行算法验证。设置的均匀半空间模型的电阻率为100Ω·m,发射源沿构造走向y方向布设,源中心点的坐标位于原点,长度为100m,电流强度为1A,测点位于x=7044m的位置。设计的3层H型模型的第1层电阻率为100Ω·m,厚度为528m;第2层电阻率为10Ω·m,厚度为200m;第3层电阻率为100Ω·m,其它参数均与均匀半空间模型保持一致,频率范围取为10-1～103Hz。图2和图3分别为采用本文算法计算的均匀半空间模型和3层H型模型的视电阻率解析解[27]与数值解结果的对比及其相对误差曲线。从图2和图3可以看出,均匀半空间模型和层状模型的视电阻率在高频段(远区)时数值解与解析解的相对误差较小,二者基本拟合;在中低频段(近区)时,均匀半空间模型的视电阻率相对误差在1.8%以内,层状模型的视电阻率相对误差在1.5%以内,误差在可接受范围内,验证了本文算法的准确性并保证了足够的精度。

图2 均匀半空间模型视电阻率(ρs)解析解与数值解结果对比(a)及相对误差曲线(b)

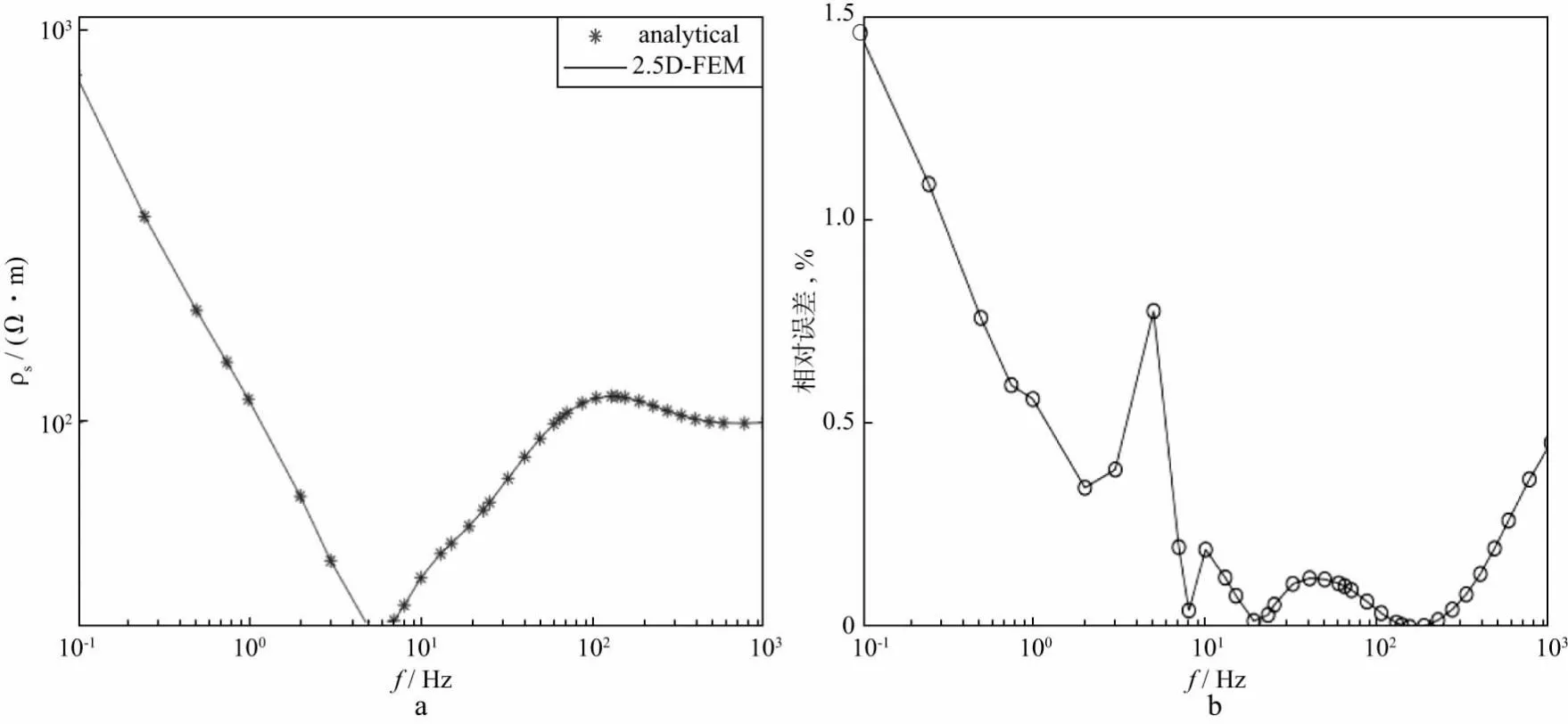
图3 3层H型模型视电阻率解析解与数值解结果对比(a)及相对误差曲线(b)

为了进一步验证本文算法的准确性,计算了100Ω·m均匀半空间下距离场源50m的测点的电场强度数值解与解析解结果,如图4所示。从图4可以看出,随着频率的降低,电场强度迅速下降;当频率降低到约25Hz后,电场幅值变化缓慢。从图4还可以看出,数值解与解析解在高频段误差较小,而在低频段二者误差略微增大,但整体的误差均小于1.6%,表明了本文算法在近区同样具有足够的精度。

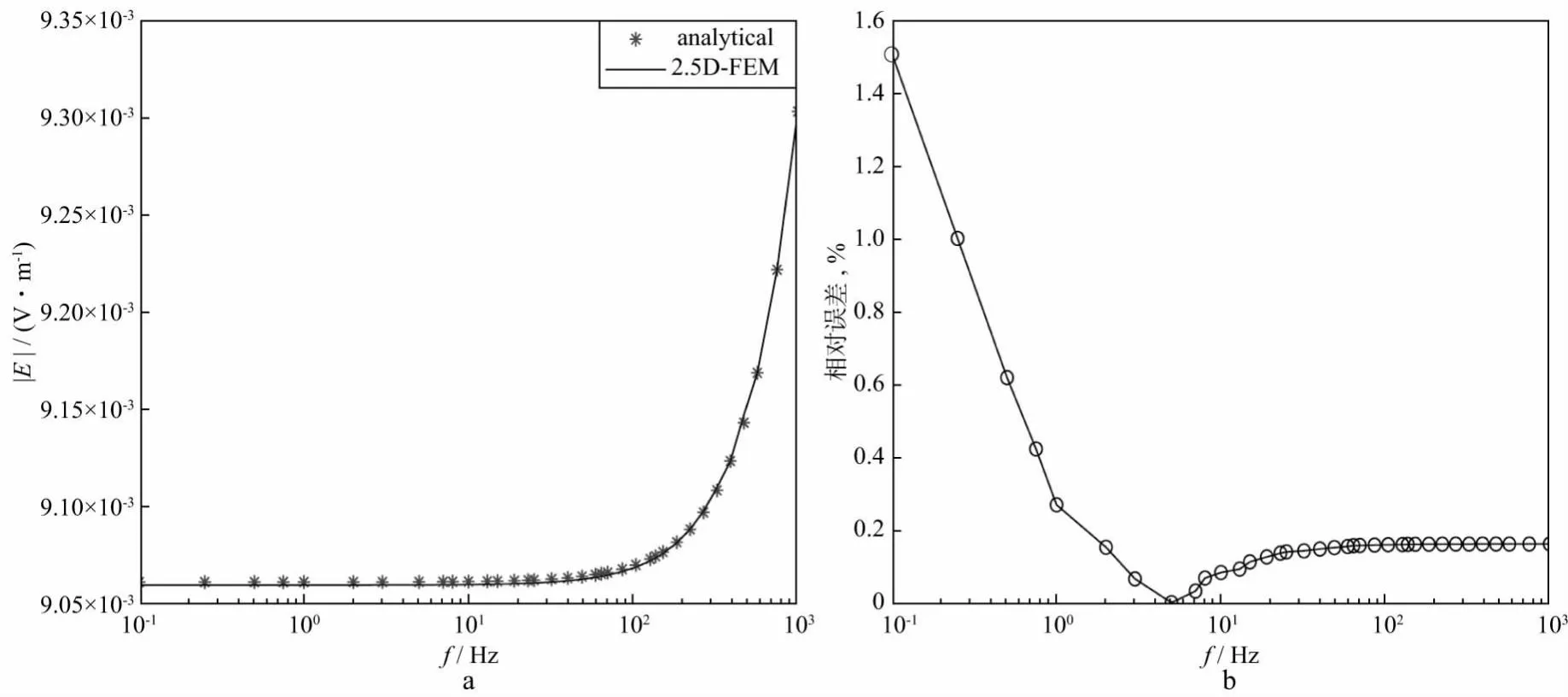
图4 均匀半空间下距离场源50m测点电场幅值数值解与解析解结果对比(a)及相对误差曲线(b)

在实际应用中,场源下方的地电结构对电磁场的影响规律至关重要。因此,首先设计了在均匀半空间条件下,场源下方存在一个电阻率为10Ω·m、埋深为428m、大小为200m×300m的二维低阻异常体模型,发射源沿构造走向y方向布设,源中心点的坐标位于原点,长度为100m,电流强度为1A。分别计算了场源下存在异常体和不存在异常体时电场和磁场的空间分布,计算结果如图5所示。从图5可以看出,当场源下方存在低阻异常体时,在场源附近及异常体所对应的深度(lgf约为1.5Hz)范围内,电场和磁场会有略微的增强,但由于场源的影响,其变化并不明显。在远区,无论场源下方是否存在异常体,二者电场和磁场的响应基本相同。计算结果表明,采用可控源电磁法探测地下低阻裂缝时,与场源下方是否存在异常体的关系不明显。

图5 均匀半空间条件下场源下方无异常体和有异常体时电场和磁场的空间分布a 场源下无异常体时电场空间分布; b 场源下存在异常体时电场空间分布; c 场源下无异常体时磁场空间分布; d 场源下存在异常体时磁场空间分布

根据页岩气水力压裂的实际情形和电导率参数,设计了二维模型来模拟水力压裂的过程,正演计算了不同模型的电场响应结果,分析了CSAMT对水力压裂裂缝位置的探测情况。在进行数值模拟时,充分考虑了钢套管的影响。

2.2 发射源靠近井

图6为二维模型示意图。在背景电导率σb=0.01S/m的均匀半空间内放置一个直径为0.1m、由550m的垂直井和一个2000m的水平井组合而成的钢套管井,以模拟水平井的压裂过程。沿着y方向布设的电偶极子长度为100m,电流大小为1A,其中心与坐标原点重合,偶极子中心与井口的距离为50m。在进行数值模拟时,钢套管的电导率设置为106S/m[48],压裂液为泥质流体,电导率取为3S/m[8]。由于钢套管和压裂液的电导率均与背景电导率差异较大,本文将钢套管和压裂液作为一个整体,并令其电导率σc=106S/m,空气电导率σair=10-8S/m。共模拟了3个水平压裂段,自右至左分别为压裂段1(stage1)、压裂段2(stage2)和压裂段3(stage3)。压裂的顺序从水平井的右端按照stage1、stage2、stage3依次向左进行。其中,stage1裂缝的水平位置为x=2000m;stage2裂缝的水平位置为x=1800m;stage3裂缝的水平位置为x=1600m。将每个压裂段生成的裂缝等效为一个宽度为0.1m、长度为200m的垂直矩形薄板(图6),裂缝内支撑剂和压裂液混合物的有效电导率σf=2500S/m[48-49]。

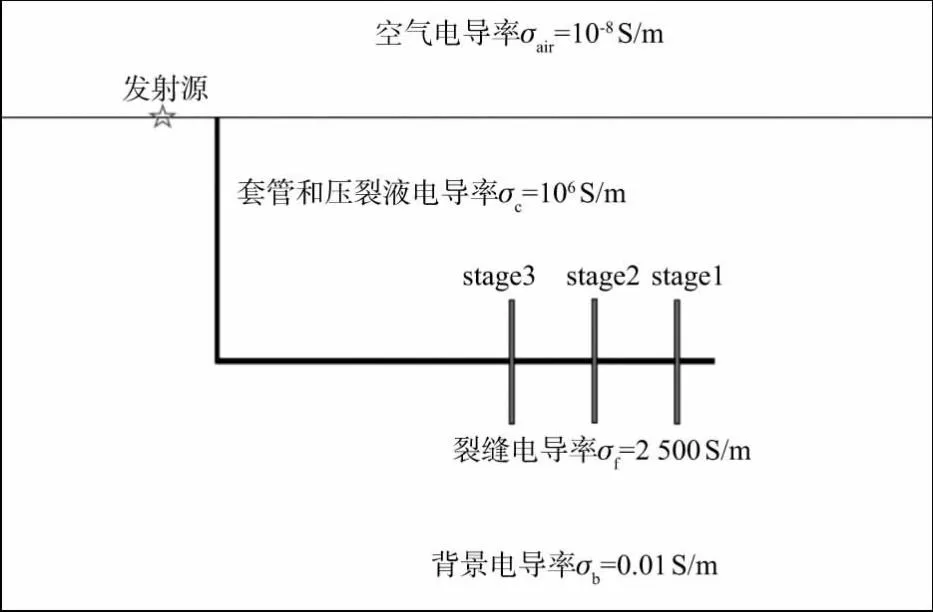
图6 发射源靠近井口时的水力压裂模型示意

测线以50m为测点间距、沿着x方向从井口向右布设,共60个测点,覆盖长度为2950m。研究区域部分网格剖分如图7所示。x、z方向的网格数分别为Nx=180、Nz=72,空气层数量为18层,地层数量为54层。其中场源、钢套管及裂缝处区域网格剖分较密,其它区域网格剖分较稀疏。场源处网格最小步长为10m;钢套管处网格最小步长为0.025m;裂缝处网格最小步长为0.02m。挑选了1,10,30,50,80,100Hz共6个频点的电场响应结果进行展示。

图7 发射源靠近井口时的水力压裂模型研究区域网格剖分示意

为了突出每个压裂段视电阻率的变化,采用(22)式对计算结果进行了相对差异处理:

(22)

式中:ρxi为第i个压裂段的视电阻率;ρxc为仅含套管(无裂缝)时的视电阻率;R1为二者取对数后的相对差异。

压裂前、后的计算结果如图8所示。其中,s1-c表示stage1与仅含套管时视电阻率的相对差异结果;s2-c表示stage2与仅含套管时视电阻率的相对差异结果;s3-c表示stage3与仅含套管时视电阻率的相对差异结果。从图8可以看出,当频率从1Hz增加到100Hz时,在对应于1200～2000m的三段裂缝的范围内,视电阻率相对差异值从负值逐渐过渡到正负相间再过渡到正值,这是因为频率越低,CSAMT方法的探测深度越深,反之越浅。根据本文设置的模型参数,当频率分别为1Hz、10Hz和30Hz时,视电阻率的相对差异值较大,此时主要反映了裂缝的视电阻率;当频率上升为80Hz和100Hz时,视电阻率的相对差异值较小,曲线主要反映了浅部结构的特征,即背景视电阻率响应;当频率大约为50Hz时,曲线主要反映了二者过渡区域的视电阻率响应特征。从图8还可以看出,曲线左侧压裂前、后视电阻率的相对差异值均为0,表明在该区域尚未生成裂缝,不同频率下3条曲线的极值均在1600～2000m,即分别对应着三段压裂的地面投影位置。当频率固定时,随着压裂进程从最右侧的stage1向最左侧的stage3移动时,每条曲线对应的极值也具有向左偏移的趋势,这是因为随着压裂过程的进行,左边不断产生新的裂缝,曲线的峰值不断地向新生裂缝的位置偏移,因此从曲线极值点可以定性和动态地反映出新生裂缝的位置。

图8 发射源接近井口时压裂前后不同频率下各压裂段与仅含套管时视电阻率的相对差异曲线a～f 频率分别为1Hz、10Hz、30Hz、50Hz、80Hz和100Hz

为了更清晰地阐明CSAMT方法对每个压裂段裂缝位置的探测情况,对相邻两个压裂段的视电阻率也进行相对差异处理,根据其视电阻率差异曲线进一步分析每个压裂段裂缝的位置情况。相对差异计算公式为:

(23)

式中:ρxi为第i个压裂段视电阻率的值;ρx(i-1)为第i-1个压裂段视电阻率的值;R2为二者取对数后的相对差异。当i=1时,R2=R1。

图9展示了对裂缝位置反映最明显的1Hz和10Hz时相邻两个压裂段视电阻率的相对差异曲线。其中,s1-c表示stage1与仅含套管时视电阻率的相对差异结果;s2-s1表示stage2与stage1视电阻率的相对差异结果;s3-s2表示stage3与stage2视电阻率的相对差异结果。从图9可以看出,随着压裂过程的持续,曲线的极小值也明显具有向左偏移的趋势,即曲线的极小值与每个压裂段所产生的裂缝的位置具有良好的对应关系。

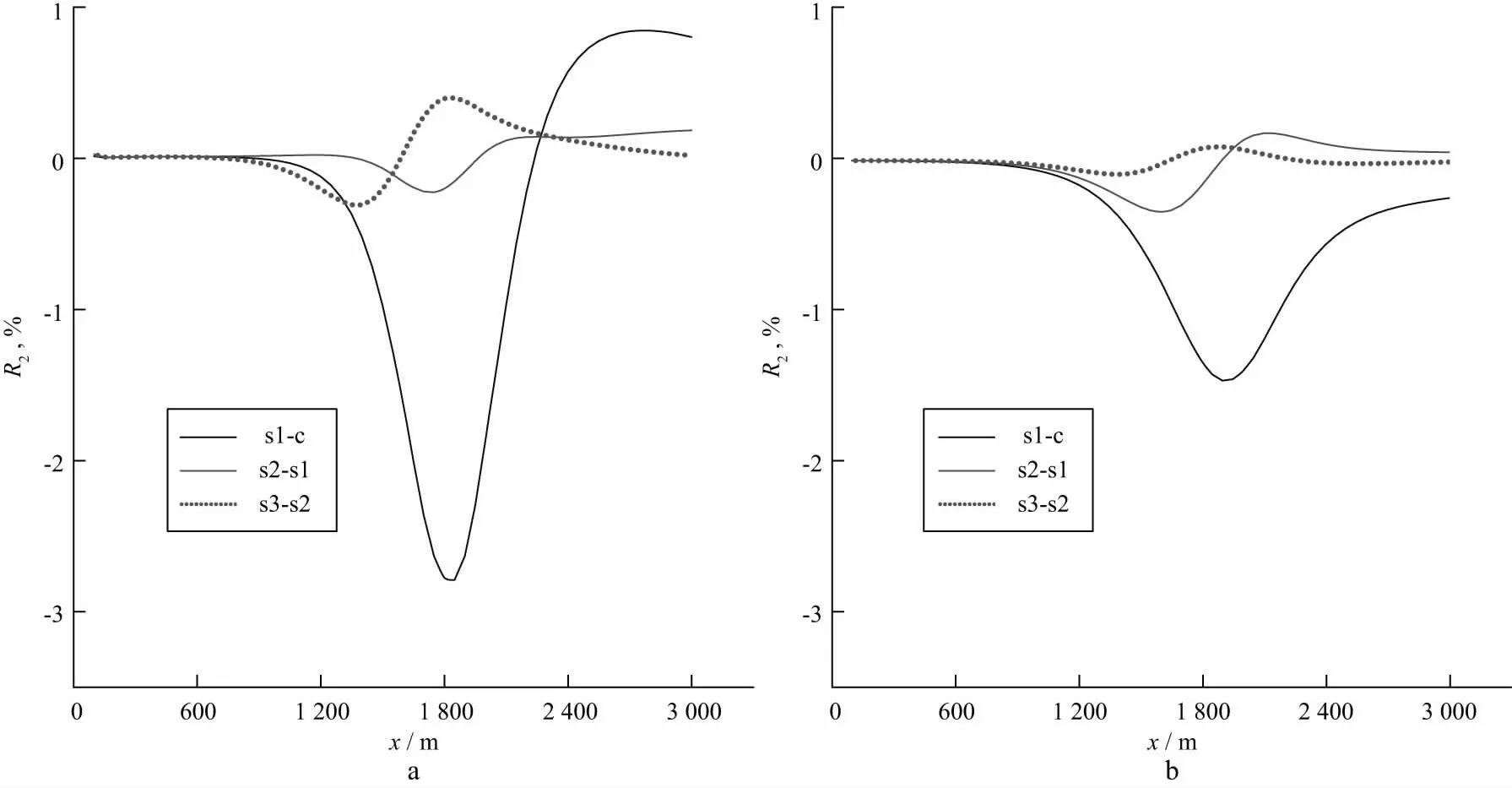
图9 发射源接近井口时1Hz(a)和10Hz(b)频率下相邻两个压裂段视电阻率的相对差异曲线

2.3 发射源远离井口

由于CSAMT法通常是在远区或波区进行观测,因此设计了如图10所示的发射源远离井口的正演模型。与发射源接近井口模型不同的是,此处垂直钢套管(井口)距发射源的水平距离增大为7600m。本次数值模拟也分为3个压裂段,压裂的顺序改为从水平井左端依次向右分别按照压裂段1(stage1)、压裂段2(stage2)、压裂段3(stage3)进行压裂(图10)。

图10 发射源远离井口时的水力压裂模型示意

其中,stage1裂缝的水平位置为x=6000m;stage2裂缝的水平位置为x=6200m;stage3裂缝的水平位置为x=6400m。128个测点以点距50m沿着x方向从3000m到9350m,长度为6350m,其余参数均与前面的模型一致。网格剖分方式除改变钢套管和裂缝的位置外,其它网格剖分方式均与图7一致(图11)。计算了1Hz,10Hz,30Hz,50Hz,80Hz和100Hz共6个频点的视电阻率响应结果,采用(22)式对数据进行相对差异处理,计算结果如图12所示。

图11 发射源远离井口时的水力压裂模型研究区域网格剖分示意

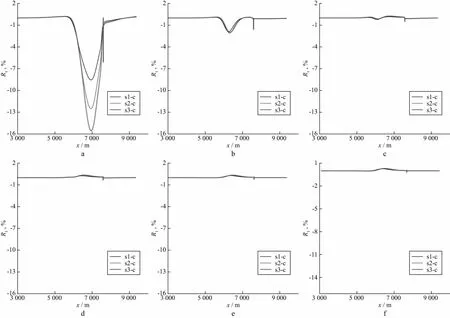
图12 发射源远离井口时压裂前后不同频率下各压裂段与仅含套管时视电阻率的相对差异曲线a～f 频率分别为1Hz,10Hz,30Hz,50Hz,80Hz和100Hz

从图12可以看出,当频率从1Hz增加到100Hz时,对应于6000～6400m的裂缝位置范围内,视电阻率的相对差异值从负值逐渐过渡到正负相间再过渡到正值,随着频率的增加,视电阻率的相对差异值也逐渐减小,其原因与图8相同,不再赘述。从图12还可以看出,在对应于6000～6400m裂缝上方的收发距位置,不论低频还是高频,视电阻率的相对差异均发生了显著变化。在同一频率下,随着压裂过程的进行,曲线的极值逐渐向右移动,即向裂缝新生成的方向发生偏移,曲线峰值不仅体现了先前压裂的旧裂缝位置,也体现出了新生裂缝的位置,表明了根据频率域可控源电磁法视电阻率的相对差异曲线对裂缝形成的位置进行初步定位是完全可行的。

为了更清晰地阐明CSAMT方法对每个压裂段裂缝位置的探测情况,同样采用了(23)式对视电阻率进行相对差异处理,即计算了相邻两个压裂段视电阻率的相对差异,根据设置的模型参数及对图12的分析,此处只展示了对裂缝位置反映最明显的1Hz和10Hz时视电阻率的相对差异结果,如图13所示。从图13可以看出,在6000～7000m范围内,s2-s1和s3-s2视电阻率的相对差异曲线呈现先增大再减小最后再逐渐增大的趋势,最终趋近于0。其中,s2-s1视电阻率相对差异曲线的极大值所对应的位置与stage2所产生的裂缝位置(x=6200m)相对应;s3-s2视电阻率的相对差异曲线的极大值所对应的位置则与stage3所产生的裂缝位置(x=6400m)相对应,即相邻两个压裂段视电阻率的相对差异极大值所对应的位置与新生成裂缝的位置一致。

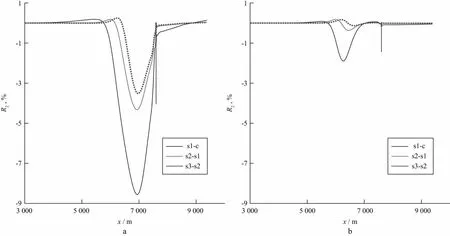
图13 发射源远离井口时频率为1Hz(a)和10Hz(b)时相邻两个压裂段视电阻率的相对差异曲线

为了更加直观地显示相邻两个压裂段视电阻率特征的变化,对图10所示模型相邻两个压裂段的视电阻率直接进行了残差处理,绘制出相应的拟断面图。图14为发射场源远离井口时相邻两个压裂段的视电阻率残差拟断面图。图14涵盖了3段水平井压裂的区域。

图14 发射场源远离井口时相邻两个压裂段的视电阻率残差拟断面a stage1与仅含套管时的视电阻率残差拟断面; b stage2与stage1的视电阻率残差拟断面; c stage3与stage2的视电阻率残差拟断面

从图14可以看出,随着压裂过程的进行,相邻两个压裂段的视电阻率发生了明显的变化。在x=6000～6400m、f=1～30Hz范围内,视电阻率的残差值较大,体现出stage1裂缝所在的大致位置。由于场源的影响会使得异常体沿着远离场源的一侧稍稍被拉伸[50],因此异常区域的中心位置与stage1所产生裂缝的中心位置并不完全一致,而是稍微偏向裂缝的右侧(图14a)。在x=6200～6600m、f=1～30Hz范围内,视电阻率的残差值也产生了相当明显的异常区域,异常区域的中心也对应于stage2所产生的裂缝中心的稍微右侧位置(图14b)。在x=6400～6800m,f=1～30Hz范围内,视电阻率的残差值异常也非常明显,异常区域的中心也对应于stage3所产生的裂缝中心稍微右侧的位置(图14c)。虽然3个压裂段的视电阻率残差的峰值与裂缝位置并不完全一致,但差异很小,因此根据视电阻率的残差响应,可以对每个压裂段所产生的裂缝进行大致定位。

3 结论

1) 随着压裂过程的进行,压裂前、后的视电阻率会发生变化,视电阻率的相对差异曲线的极值会朝着裂缝新生成的方向偏移,其移动的方向和范围与新生裂缝的位置具有良好的对应关系。根据视电阻率的相对差异曲线极值的位置可以对裂缝进行大致定位。

2) 在裂缝所对应的位置处,视电阻率产生了足够大的残差值,但由于受到场源的影响,异常区域的中心与裂缝的中心并不一一对应,而是稍微偏向裂缝位置的右侧。根据相邻两个压裂段视电阻率的残差结果可以对裂缝的位置进行初步定位。

3) 从计算结果还可以看出,无论是在近区还是远区观测,频率域可控源电磁法的视电阻率对裂缝的响应特征是一致的,即视电阻率的相对差异极值偏移的方向均与裂缝新生成的方向一致。因此,可以根据曲线极值的偏移对新生裂缝的位置进行初步定位。计算结果表明了频率域可控源电磁法对于水力压裂裂缝的定位是可行的。本文的研究对于指导页岩气与干热岩等致密储层的水力压裂监测具有参考价值。