基于聚类原理的涡扇发动机飞行剖面逐步分类方法

赵丽娜，段垚奇

（国机集团北京飞机强度研究所有限公司，北京 100083）

0 引言

飞行任务剖面分类是航空发动机载荷谱编制的环节之一，通过对上百个实测飞行起落的数据分析，归并出航空发动机若干个典型任务剖面作为所有任务剖面的代表。任务剖面的分类不仅为编制任务混频及载荷谱提供依据，还可用于疲劳损伤分析，进而确定或延长发动机的使用寿命［1］。

飞行任务剖面分类首先需要确定分类的依据，即能表征任务剖面特征的实测飞行参数或者某些特征参数，然后运用聚类等统计方法进行剖面分类。

在剖面分类的依据选择方面，张海威等［1］、程德金［2-3］等均选取飞行高度、马赫数及油门杆角度3 个参数描述发动机飞行任务剖面；郝晓乐等［4］选取13 个飞行参数共77 个统计量作为任务剖面归纳的原始载荷矩阵；宋迎东等［5］选取飞行高度、马赫数、发动机转速及发动机重心法向过载4 个参数，通过主成份分析，最终选用了累计贡献率达到80%以上的第一、第二主成份进行分类，将4 维空间的飞行任务剖面分类问题转化为二维平面内的分类问题；杜宇飞等［6］选取飞行高度和马赫数作为划分飞行任务剖面的参数。在剖面分类所用的统计方法方面，张海威等［1］、程德金［2-3］以涡喷发动机为研究对象，采用Fuzzy 聚类方法，通过建立任务剖面样本的隶属函数模糊矩阵、检查矩阵是否模糊等价、满足时选取不同阈值进行动态聚类，然后确定发动机典型任务剖面；郝晓乐等［4］采用系统聚类法、主成分聚类法、模糊聚类法对71 个飞行剖面进行了聚类归纳，对比分析表明，系统聚类法更能充分反映该类任务剖面的共同特点和属性；宋迎东等［5］采用主成份聚类法将4 维空间的飞行任务剖面分类问题转化为二维平面内的分类问题，然后用重心法进行了定量聚类；杜宇飞等［6］采用散点图法将飞行高度和马赫数的空中飞行段均值绘制在一张图上，形成聚类散点图，然后利用聚类原理将31个飞行任务剖面划分为五大类型。

综上，发动机飞行任务剖面分类，一是选择的飞行参数及其特征值不同，二是选用的聚类方法不同，包括：模糊聚类法、主成份聚类法、系统聚类法、聚类散点图。

模糊聚类法的优点在于飞行剖面之间的相似程度能通过隶属函数来定量地表示，但是分类时使用的入阈值是人为确定的，大小不同会直接影响分类的“粗细”，而且当飞行剖面样本量大时，模糊矩阵阶数加大，工作量大增。主成份聚类法的优点在于通过主成份分析实现参数的降维，使后续统计得到简化，但同时也因为非主成份的舍弃在可接受的范围内造成了分类的偏差。系统聚类法采用类平均法计算类与类之间的距离，考虑了类内每个元素，分类更为精确。以上方法均属于定量聚类，克服了分类时的主观性，但是当飞行剖面样本量大时，并类步数增多，比较复杂，而且存在距离的大小直接影响分类的“粗细”问题。聚类散点图通过图上的散点来表征样本的特征值，利用聚类原理直观地进行分类，计算简便，但适用于表征样本的特征值不超过2 个的情况。

本文以涡扇发动机为研究对象，考虑涡扇发动机为双转子结构，选用飞行高度、马赫数和转速3个参数作为飞行任务剖面的分类依据。该发动机飞行剖面较多，由于散点图聚类法计算简便和分类直观，选择聚类散点图进行分类，但表征飞行剖面的参数共3个，而散点图法适用于2个特征值的情形，据此本文提出了逐步分类法，将特征值逐步降维，最后运用二维散点图完成剖面归类。

1 方 法

1.1 参数选择

涡扇发动机的工作特性主要取决于飞行高度、飞行速度和发动机转速3个参数［7］，发动机的供油量按照高压转子或低压转子的转速进行调节，因此，本文对涡扇发动机飞行剖面分类时选择飞行高度、飞行马赫数和低压转子转速3个参数。

1.2 实测参数载荷谱特征提取

发动机通过装机飞行实测可获得不同的飞行起落，有的飞行起落包含多个飞行任务剖面，因此，首先要对飞行起落按照任务剖面进行拆分，获得实测飞行任务剖面。由于每个任务剖面的飞行时间长短不同，假设飞行实测获得N个飞行任务剖面，则飞行剖面的分类问题即转化为N个长度不同的三维向量组的归类问题，比较复杂。

为简化归类问题，对3 个参数的时间历程数据进行分析，考虑到不同飞行剖面的起飞段和降落段3 个参数的变化规律基本相同，因此，主要考虑空中段数据。飞行高度时间历程在空中时相对平稳、变化不大，飞行马赫数时间历程在空中时有频繁的小幅变化，转速时间历程在空中时变化幅度较大。通过对比，确定将每个飞行剖面的飞行高度最大值、飞行马赫数空中段均值和转速空中段二阶矩分别作为飞行高度、飞行马赫数和转速载荷谱的特征值，用于飞行剖面的分类。

为更好地反映飞行剖面中飞行马赫数、转速的变化情况，也为了方便后续编制发动机载荷谱考虑，在计算飞行马赫数均值、转速二阶矩前对其时间历程进行有效峰谷值压缩，然后采用峰谷值压缩结果计算特征值。

1.3 聚类分析（散点图）

散点图是多元统计分析中可视化分析方法之一，将表征某个事物的多个参数以散点的形式绘制于图中，从而方便直观统计分析［8］。

涡扇发动机的飞行剖面由飞行高度最大值、飞行马赫数均值和转速二阶矩来表征，设第i个飞行剖面为Pi，则

式中：himax，分别为第i个飞行剖面的飞行高度最大值、飞行马赫数均值和转速二阶矩。将所有实测飞行剖面的Pi绘制在一张三维上，则可得到飞行剖面的三维散点图。三维散点图比较复杂，不便直接分类，因此，本文提出了逐步分类法。

1.4 逐步分类法

设实测飞行剖面共N个，则每个实测飞行剖面的飞行高度最大值组成的数组

H的变异系数

式中：CVH为所有飞行剖面飞行高度最大值数组的变异系数，表示各飞行剖面的高度最大值的离散程度；σH为标准差；μH为均值。同理，依次计算其他2个参数数组的变异系数CVMa，CVn。

比较3 个参数数组的变异系数，选取变异系数最小，即离散程度最小的参数，首先，按照该参数进行聚类分析，进行第1 次分类；然后，在第1 次分类的基础上，绘制由其他2 个参数构成的二维散点图，据此进行第2次分类。

1.5 飞行剖面分类流程图

飞行剖面分类的流程图如图1 所示。

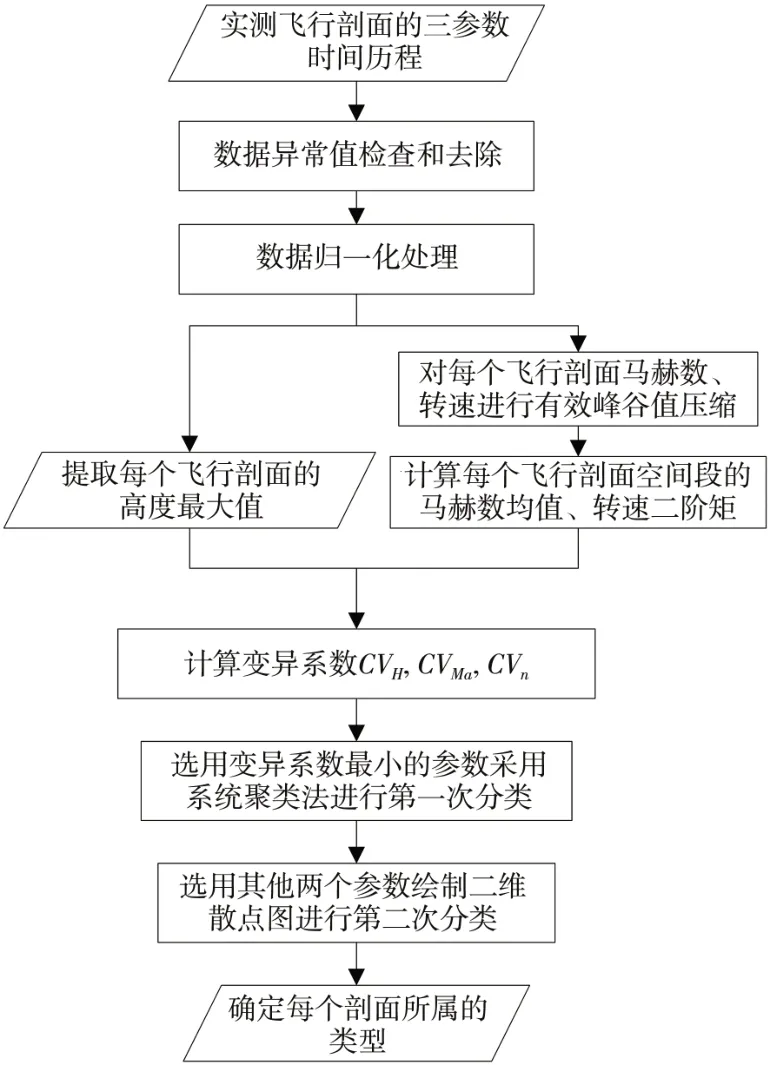
图1 飞行剖面分类流程图Fig.1 Flow chart of classification of flight profile

2 实例与结果

本文以某型涡扇发动机为研究对象，通过飞行实测得到87 个飞行剖面，其中1 个飞行剖面的飞行高度、飞行马赫数及低压转子转速时间历程曲线（分别除以某一固定值进行归一化处理）分别如图2～图4 所示。

图2 某一飞行剖面的高度时间历程Fig.2 Altitude time history of one flight profile

图3 某一飞行剖面的马赫数时间历程Fig.3 Mach number time history of one flight profile

图4 某一飞行剖面的转速时间历程Fig.4 Rotation speed time history of one flight profile

2.1 飞行剖面的参数特征值

根据飞行剖面的3 个参数时间历程分别计算各飞行剖面飞行高度最大值hmax、飞行马赫数-----Ma均值及低压转速二阶矩E(n2)。

在对飞行马赫数时间历程进行有效峰谷值压缩时，阈值选择0.008 2。在对低压转速时间历程进行有效峰谷值压缩时，阈值选择0.02。

由于飞行实测任务剖面较多，因此表1 列出了部分飞行实测任务剖面的 3 个参数特征值。

表1 部分飞行剖面的 3 个参数特征值Tab.1 Characteristic values of the three parameters of some flight profiles

2.2 三维散点图

将每个飞行剖面的飞行高度最大值、空中段马赫数均值、空中段低压转速二阶矩作为一点绘制于一张三维图上，即获得了飞行剖面三维散点图，如图5 所示。从图中可见，利用三维散点图直接分类并不可行。

图5 飞行剖面三维散点图Fig.5 3D scatter diagram of all flight profiles

2.3 逐步分类

3 个参数特征值数组的变异系数如表2所示。

“我的图书馆”功能模块主要向用户提供“绑定/解绑图书证”“新闻公告”“馆藏查询”“我的借阅”4类服务。

表2 变异系数Tab.2 Coefficient of variation

如果特征参数的变异系数低于5%，则可以认为各飞行剖面的该特征参数差异不显著，可不再将该参数作为分类依据。

从表2 中可见，3个特征参数的变异系数均大于5%，分类时均应考虑。低压转速二阶矩的变异系数最小，说明各飞行剖面低压转速的离散程度最小，各飞行剖面的低压转速差异最不明显。

首先，根据低压转速进行第1次分类。选用系统聚类分析法，设共有n个飞行剖面，分类步骤为：

1）将每个飞行剖面独自聚成一类；

2）选用组间平均距离法，把“距离”较近的2 个飞行剖面聚合为一类，其他的飞行剖面仍各自聚为一类，共聚成n-1类；

3）将“距离”最近的2 个类进一步聚成一类，共聚成n-2类；

4）重复步骤3），最后将所有的飞行剖面聚成2类；

5）计算2 个新类的变异系数，如低于5%，第1次分类结束；如大于或等于5%，则分类数加1，直至每个新类的变异系数低于5%。

利用SPSS 软件的系统聚类法进行聚类分析，分为2类，结果如表3 所示。

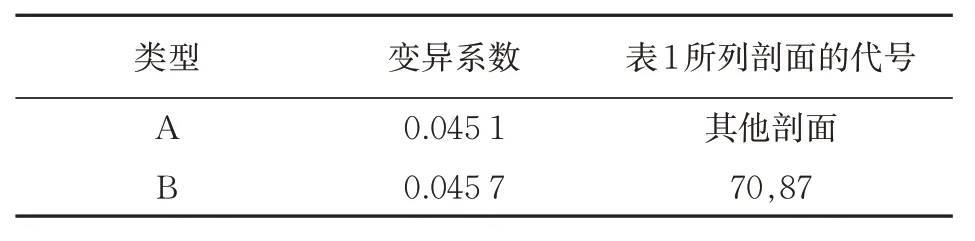
表3 第1次分类结果Tab.3 First classification results

然后，根据高度、马赫数进行第2 次分类。将第1 次分类结果中每类的所有飞行剖面的高度最大值、马赫数均值绘制于一张图上，得到马赫数-高度二维散点图，如图6 所示。

根据聚类原理，并结合飞行高度常规划分规则及飞行马赫数常规划分规则（见表4），按照A类飞行剖面的分布将其分为5类，B类飞行剖面主要分布在1个区域，归为1类。

表4 飞行高度、马赫数常规划分规则Tab.4 Conventional division rules for flight altitude and Mach number

2.3.1 低空低速剖面

将飞行高度小于0.1，马赫数小于0.35 的剖面划分为低空低速剖面，即区域①。其中一个剖面的参数时间历程如图7 所示。图中黑色曲线表示原始时间历程图，点表示经过有效峰谷值压缩的空中段数据。

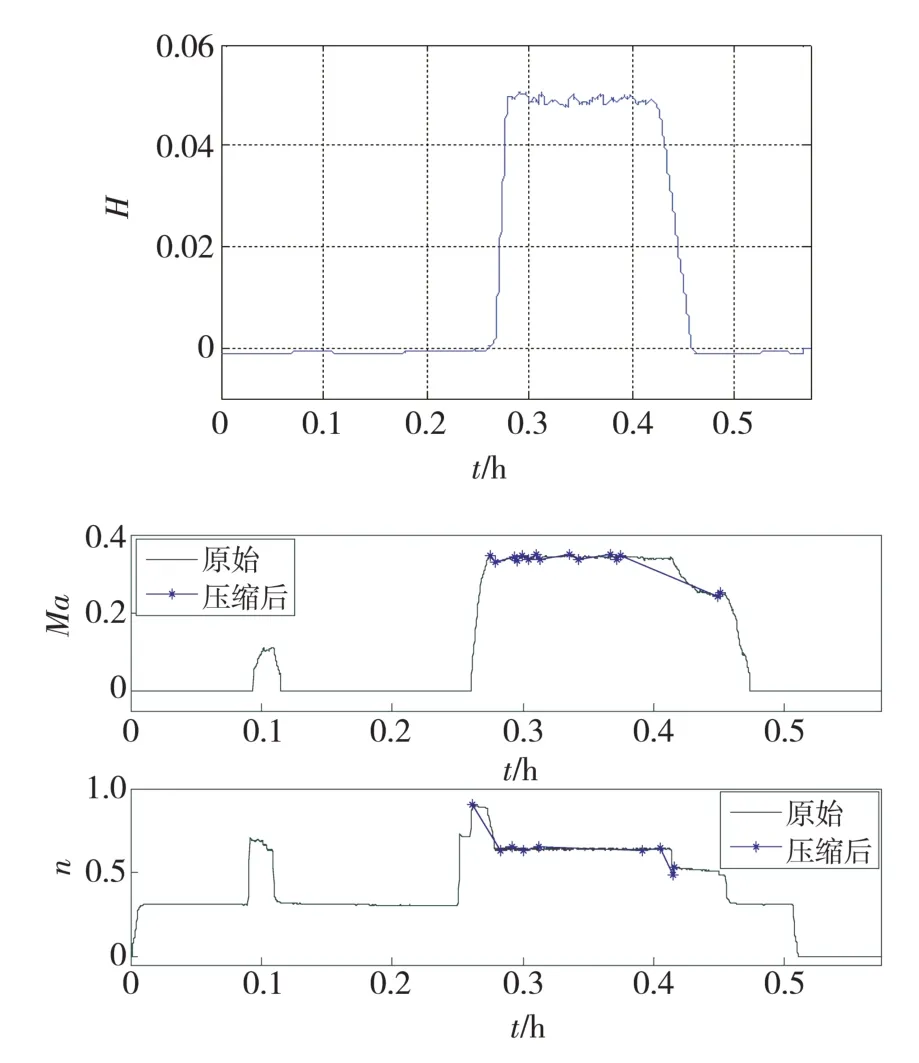
图7 低空低速飞行剖面Fig.7 Flight profile with low altitude and low speed

2.3.2 一类中空亚音速剖面

将飞行高度大于0.1且小于0.4，马赫数大于0.35的剖面划分为一类中空亚音速剖面，即区域②。其中一个剖面的参数时间历程如图8 所示。

图8 一类中空亚音速飞行剖面Fig.8 The first kind of hollow subsonic flight profile

2.3.3 二类中空亚音速剖面

将飞行高度大于0.4且小于0.55，马赫数大于0.35的剖面划分为二类中空亚音速剖面，即区域③。其中一个剖面的参数时间历程如图9所示。

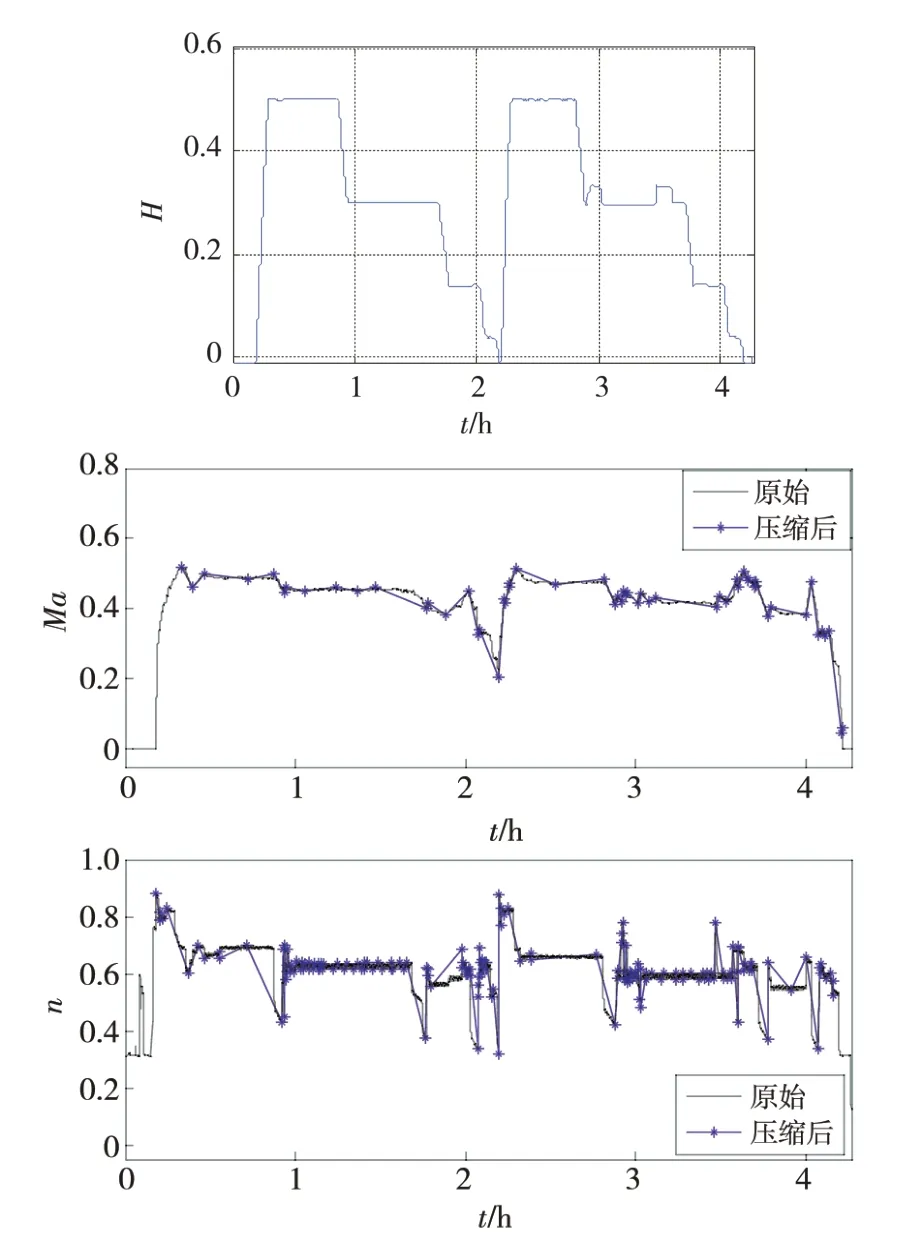
图9 二类中空亚音速飞行剖面Fig.9 The second kind of hollow subsonic flight profile

2.3.4 三类中空亚音速剖面

将飞行高度大于0.55且小于0.7，马赫数大于0.35的剖面划分为三类中空亚音速剖面，即区域④。其中一个剖面的参数时间历程如图10所示。

图10 三类中空亚音速飞行剖面Fig.10 The third kind of hollow subsonic flight profile

2.3.5 一类高空亚音速剖面

将飞行高度大于0.7且小于1，马赫数大于0.35的A类剖面划分为一类高空亚音速剖面，即区域⑤。其中一个剖面的参数时间历程如图11 所示。

图11 一类高空亚音速飞行剖面Fig.11 The first kind of high-altitude subsonic flight profile

2.3.6 二类高空亚音速剖面

将飞行高度大于0.7且小于1，马赫数大于0.35的B类剖面划分为二类高空亚音速剖面，即区域⑥。其中一个剖面的参数时间历程如图12 所示。

运用聚类分析和散点图，通过逐步分类法对表征飞行剖面的3个参数进行了多元分析，将实测的87个飞行剖面划分为6类。表1 所列的部分飞行剖面的分类结果如表5 所示。对分类结果进行分析，飞行科目相同或相近的飞行剖面被划分为一类，分类结果准确，该分类方法有效。

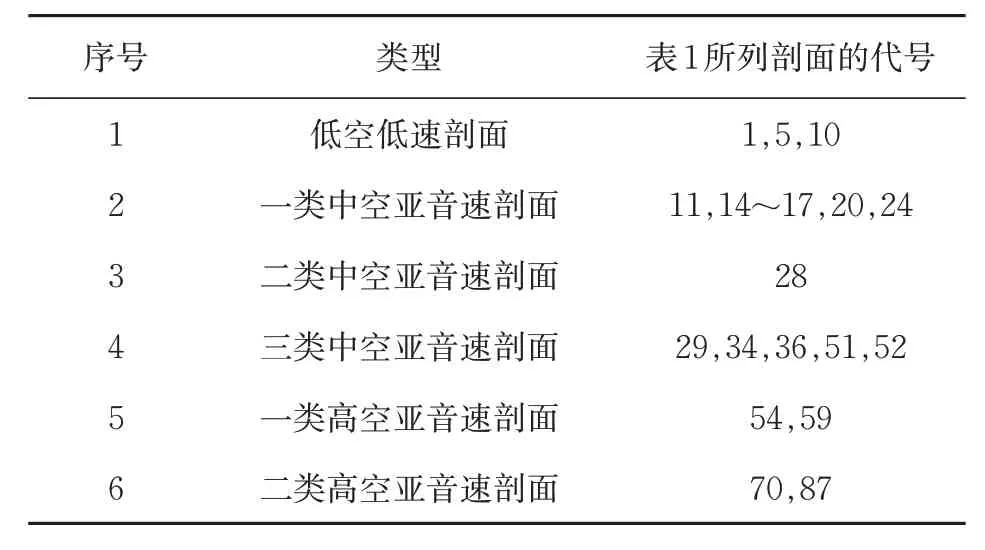
表5 第二次分类结果Tab.5 Second classification results

3 结论

本文对涡扇发动机飞行实测任务剖面的分类问题进行了研究，结论如下：

1）基于涡扇发动机的性能参数选择了高度、马赫数和转速3 个参数作为表征飞行剖面种类的参数，将二维问题上升为三维问题。

2）通过参数的变异系数判断表征飞行剖面的参数的离散程度从而识别飞行剖面之间差异显著和不显著的参数，根据离散程度进行逐步分类；对变异系数小、离散程度低的参数采用系统聚类法进行第一次分类，再运用二维散点图进行第二次分类；采用逐步分类法实现了降维处理，将系统聚类法和散点图法相结合，成功将某涡扇发动机的87个实测飞行剖面划分为6类。

3）分类结果显示，飞行科目相同或相近的飞行剖面被划分为一类，分类结果准确，分类方法有效且直观方便。

4）飞行剖面分类的选参问题，即选用哪些参数、选用多少参数既能保证飞行剖面分类的准确性又符合经济性要求有待进一步研究。

5）采用本文方法与其他文献方法对飞行剖面进行分类有待进一步对比研究。