溃堤洪水在有压雨水管网街区演进的试验研究

张晓雷，刘书瑜，董柏良，赵建坤，张立涛

(1.华北水利水电大学水利学院，河南郑州 450046；2.河南省水圈与流域水安全重点实验室，河南郑州 450046；3.武汉大学水资源与水电工程科学国家重点实验室，湖北武汉 430072；4.广东省水利水电科学研究院，广东广州 510610)

近年来随着城市化进程的快速发展，街区地面硬化率显著提升，深刻改变了原有的水文条件，致使城市洪涝频发。2021年，郑州“7·20”洪水造成了省域内150个县（市、区）1 453.16万人受灾，直接经济损失高达1 142.69亿元。持续的强降雨天气致使多地河道、水库内部水位急剧爬升，对下游平原城市造成了潜在的危险[1]。

城区河道一旦发生决口，溃堤洪水的流速、水深将对河道两岸人民群众带来难以估计的损失[2]。溃口在溃堤波演进过程中逐渐展宽，溃口流量在短时间内迅速增至最大[3]，随后河内水位逐渐下降且下降速率逐渐减小[4]，且河床断面的冲淤特性取决于洪水过程的流速变化与床沙起动临界流速[5]，当溃口两侧水位差不变时，溃口流量稳定[6]。董柏良等[7]先是开展了溃堤洪水演进的概化物理模型试验，定量分析了不同街区构造对洪水演进过程的影响，随后基于数值模拟识别了人和车辆在洪水过程中的风险[8]。雨水管网系统作为城区的主要排水措施，其泄流能力是应对城市洪涝灾害的关键因素之一。雨水口作为城市雨水管网系统的主成分之一，其泄流量对于城市的防洪减灾至关重要。

与极端暴雨相比，设计重现期内的暴雨强度致使城区的雨水管网为无压流，而雨水管网在极端暴雨下则极易形成有压流。目前，雨水管网在无压流状态下，常采用堰流公式及管嘴出流公式确定雨水口的泄流量[9]，Mustaffa[10]及Martins[11]等分别针对雨水口的排列方式以及种类对泄流量的影响开展了相关模型试验，并根据试验数据对泄流公式确定了相应的泄流系数。为了进一步地研究雨水口在真实环境下的泄流能力，一些学者开展了针对道路坡降[12–13]、雨水口堵塞[14]及其涡流场[15]对雨水口泄流能力影响的物理模型实验。同时，Leandro等[16]采用LESSmagorinsky湍流模型重点分析了雨水口井筒内部的湍涡结构，然而，在管嘴出流状态下雨水口表层出现的湍涡结构给数值模拟研究带来了巨大的挑战，特别是位于道路中心处的雨水口更是难以复现：赵建坤[17]建立的3维数学模型仅能模拟出在堰流条件下平篦式雨水口的3维流场；周浩澜等[18]分别采用边界法、设定高程法、人工加糙法以及容积率方程法均未模拟出雨水口表层的湍涡结构。张珂等[19]基于Fluent建立的数学模型不仅能够模拟出道路边上雨水口的湍涡结构，还构建了雨水口下泄流量系数与篦前水流的弗劳德数之间的经验公式。以上研究成果虽然能够定量地描述了在无压状态下雨水管网的泄流能力，但当城市发生极端暴雨时，雨水管网应为有压状态，在此条件下，雨水口的泄流量将会受到限制[20]。因此，上述研究成果中的雨水口泄流量不能精准地反映出在极端暴雨下城市的泄流能力。目前，已有研究学者针对有压雨水管网的泄流能力开展了相关的数值模拟。譬如Geng[21]和Jorge[22]等对雨水口堰流、淹没出流两种形式先后通过CFD及SWMM分析了有压雨水管网的泄流能力。秦磊等[23]重点研究分析了雷诺数对有压雨水管网的分流干扰。侯精明[24]、童旭[25]、徐卫红[26]等通过数值模拟分别研究了陕西西咸新区、成都中心城区、天津中心城区在不同暴雨条件下的内涝程度。此外，地表径流与雨水管网交互耦合的水力计算常通过搭建耦合数学模型进行求解，其中地表径流多采用2维浅水方程进行数值模拟，而雨水管网则是基于SWMM的基本方程搭建数学模型[27–28]。

综上所述，当城区发生极端暴雨时，城区河道存在溃堤的隐患，且雨水管网的水力条件复杂多变，雨水管网的泄流能力长期处于超载状态，溃堤洪水在有压雨水管网街区的演进需进一步研究分析。为此，本文建立了典型城市街区的概化水槽模型，研究了溃堤洪水在有压雨水管网街区的演进过程，定性分析了街区水跃区域的迁移变化，定量分析了街区水位的波动变化及有压雨水管网的泄流能力。

1 实验装置及方法

1.1 实验装置及测量仪器

研究基于典型街区建立概化水槽模型，模型结构及测量仪器的布置如图1所示。在空间上典型城市街区的概化水槽模型可划分为试验水槽和雨水管网上下两层，水槽由进水前池和城市街区构成。

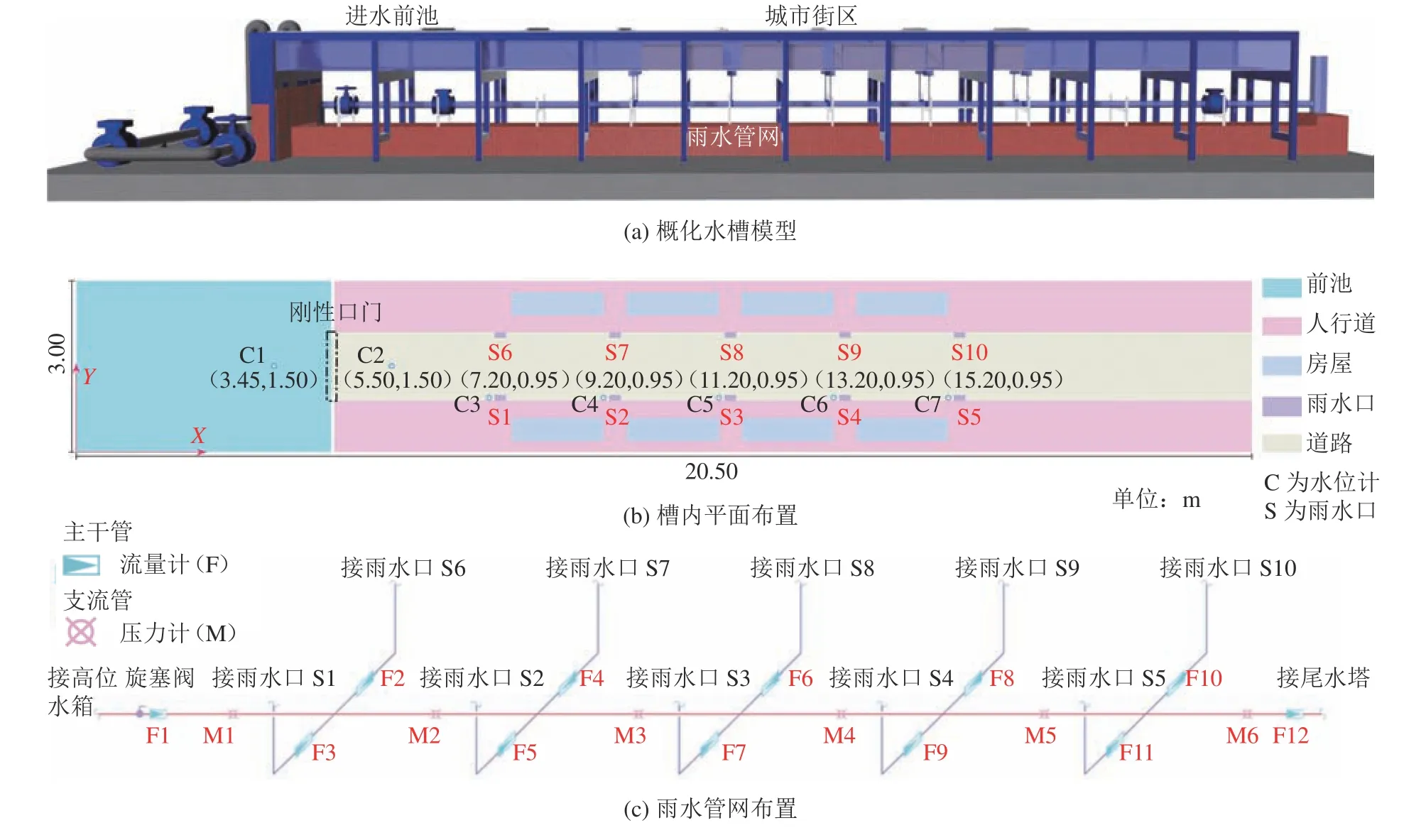
图1 概化水槽模型及测量仪器布置Fig. 1 Layout of the generalized sink model and positions of measurement equipment

图1（a）中，给出了本试验采用的概化水槽模型。图1（b）中：水槽全长20.50m，宽3.00m，高0.60m，水槽底部和边壁均由钢化玻璃组成，水槽底坡为0，水槽边壁与底部垂直衔接。模型进水前池长4.45m，宽3.00m，前池通过2根进水管供水，管流流量可通过阀门及电磁流量计进行调节；前池出口处设置了一个刚性闸门，长0.05m，宽1.00m，通过瞬间拔起闸门挡板以模拟河道溃堤的现象。街区由道路、雨水口、人行道和房屋构成。道路长16.00m，宽1.20m，在人行道两侧处共计布置了10个雨水口（S1～S10）；雨水口长0.20m，宽0.10m，雨水口S 1和S 6距离上游挡板2.8 0m，雨水口间距1.80m；人行道布置在水槽两侧，长1 6.0 0 m，宽0.90m，相对槽底高0.0 1 m；人行道上布设了2排4列的房屋，房屋长、宽、高分别为1.60m、0.40m和0.50m，房屋间距0.4 0m，房屋距离水槽侧壁0.2 0m，雨水口S1和S6附近的房屋距离前池下游挡板3.10m。由图1（c）可见：街区的雨水管网由一条主干管和10条支管组成，干管坡度为0.28%，主干管管径为150mm，管内底距槽底0.825m，主干管通过上游处的阀门及电磁流量计控制管路流量，下游配有电磁流量计读取管网泄流总流量，管内压强由长宽均为0.30m，高1.20m的尾水塔控制，管内压强通过压力计读取。雨水支管管径为25mm，上游连接雨水口的井身，下游与排水干管直接相连。由于试验条件限制，街区雨水管网中没有考虑实际排水干管与连接管交汇处的检查井结构。管网系统配有电磁流量计以监测各个雨水口及其支管的泄流量。

水槽侧壁上方架设平行导轨，搭载带有超声波水位计的横梁式移动平台，结合W I M StarFish-LY08自动水位测量系统监测街区典型位置的水位变化。由图1（b）可见，水位计C1和C2布置在刚性口门两侧，距口门挡板均为1.00m，C3～C7分别布置在雨水口S1～S5的正前方0.10m。水位计C1用于测量进水前池的水位高度，C2～C7用于监测街区水位场对溃堤波的响应，其中，C3～C7读取雨水口S1～S5附近的水位高度。由图1（c）可见，排水主干管管底均匀布置了6个压力计（M 1～M 6），压力计间距2.00 m，结合Data ManagerTool-V3.09.2自动测量系统读取雨水主干管的压力分布。M 1和M 6用以反应主干管在进出口处的总压变化，M 2～M 5用以监测雨水口泄流对管内压降的影响。管路系统共布设了12个电磁流量计F1～F12，再通过LMAGMODRTUV 7 7读取示数。电磁流量计F1和F12分别布置在排水主干管进出口，F2～F11分别布置在各个排水支管中间，F1和F12用以读取有压雨水管网进出口处的总流量，其中，F2～F11用以读取雨水口泄流流量。

1.2 试验工况及步骤

试验假定雨水主干管流量Q1及压强P0保持恒定，进水前池的水深H及进口流量Q2不同，具体试验工况见表1。

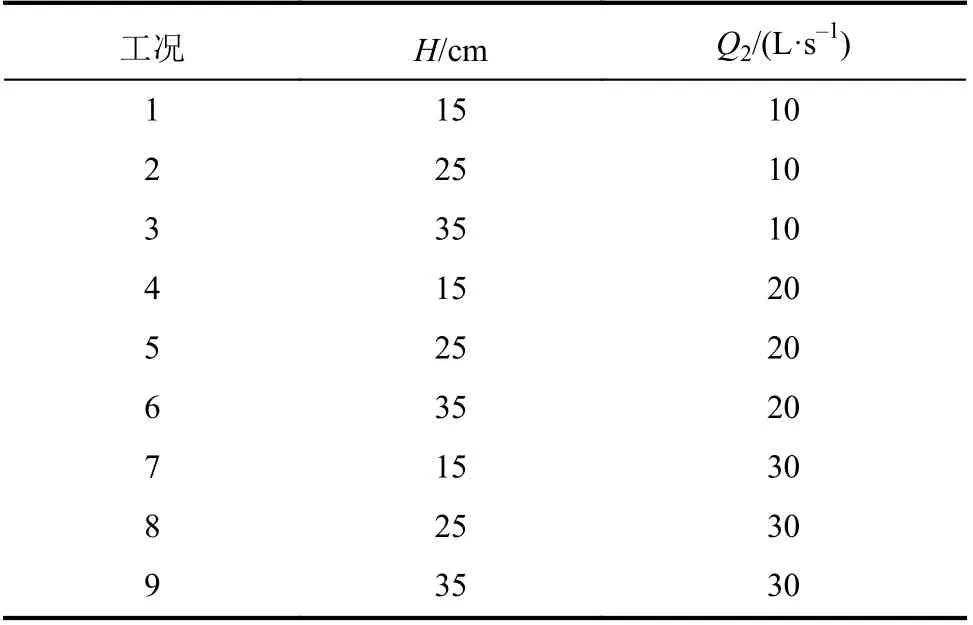
表1 模型试验工况Tab.1 Summary of experimental cases

实验开始前，先调节主干管的阀门以获取恒定流，再通过调节尾水塔排出主干管因充水导致的滞留气泡，此时雨水管网为满管有压流状态，并且各支管管内存在一定的水柱高度。实验开始时，刚性闸门关闭，通过调节阀门及电磁流量计使2根输水管以恒定流注入进水前池，当进水前池内部的水位爬升至特定水位时，迅速拔起刚性闸门挡板，城市街区发生溃堤洪水演进，口门两侧水位差值迅速降低，溃堤洪水通过雨水口和水槽尾门排出。当300 s后槽内水位场无明显波动时，停止向前池供水，数据采集完毕。

1.3 实验重复性

试验仪器需测定流速大、水深浅、流态变化复杂的溃堤洪水以及流量和压强瞬时变化剧烈的管网系统，测量数据的不确定性较大。此外，由于试验过程中需通过人工拔出刚性口门挡板以形成溃堤洪水，该试验存在着较大的人为误差。因此，为确保试验结果的真实性，各试验工况均重复两次以上。图2给出了工况5在两次试验中的槽内水位、管路流量及压力水头的对比结果。其中，通过求解皮尔逊相关系数以分析多次重复试验的相关性，求解公式如下：

式中，n为样本X或Y的数据个数，和分别为样本X和Y的均值，Xi和Yi分别为由i在样本X和Y中索引的实测数据。

由图2可知，工况5的水位、流量及压强试验结果相关性均大于0.930。

因此，不论是槽内水位的波动变化，还是雨水管网的流量及水头的瞬时变化，重复性试验结果相关性较高，表明试验条件控制精准，试验过程可重复，试验结果真实有效。

图2 重复性试验结果对比Fig. 2 Comparison between repetitive experiments

2 实验结果及分析

2.1 街区水位对溃堤洪水的响应

图3给出了溃堤洪水（工况6）在街区的演进过程。由图3可见：当口门开启时，前池水体的重力势能转换为动能，在房屋及边界的作用下，溃堤洪水以薄层状水片依次在2.7、3.4和5.1 s爬升前三列房屋建筑，随后掺和大量气体发生翻卷，在建筑物附近形成局部水跃。水跃现象由房屋建筑物的局部区域迁移至街区道路，并在5.1 s完成交汇；交汇后的水跃区域逐渐向街区上游演进，且在16.1 s时演进至最上游，随后向下游移动，水跃区域在人行道的作用下先后在人行道及道路消失；街区内的水跃现象在30 s基本消失，此后街区水位逐渐减小，街区水位在溃口两侧水位差值稳定时不再发生明显波动，此时街区洪水在人行道、房屋及水槽边壁的作用下形成絮状波纹。试验采用水位计C1～C7详细地记录了街区水位在溃堤洪水演进过程中的波动响应，由于C2～C7的水位时间过程曲线的变化规律总体相似，图4给出工况3～6及工况9的部分测点数据。C2～C7的水位随着溃堤波的传播扩散整体呈先增大、后减小的变化趋势，当溃口两侧水位差值稳定时，各测点处的水位逐渐趋于平稳。

试验通过工况3、6和9用以研究槽内水位场在进水前池蓄水高度H相同，进口流量Q2不同条件下的波动变化。当刚性口门挡板拔出时，不同工况在C1处的水位变化相近，在0～10s、10～30s期间内水位均减小了12.0 cm；随后，溃口洪水的能量主要源于进水前池提供的动能，C1的水位变化随着进口流量的增大而减小，在30～100 s期间内水位分别减小了6.0、5.1和4.7c m。由此可知，在0～3 0 s内溃口洪水的能量主要源于前池蓄水高度形成的位能，在30 s后溃口洪水的能量主要源于前池进口水流的动能。C2～C7几乎在相同时刻达到了各自的峰值水位，各测针水位的减小速率随着前池进口流量的增大而减小，街区水位场在100 s后达到稳定。当街区水位场稳定时，在各工况下C5的水位高度分别为1.714、2.141和2.338 cm，C3～C7水位在房屋的作用下呈先增大、后减小的变化趋势，在工况6恒定流状态下C3～C7的水位高度分别为2.20、2.21、2.37、2.23和1.76 cm。

试验通过工况4、5和6用以研究进水前池进口流量Q2相同，蓄水高度H不同状态下溃堤洪水的演进过程。结合前文可知，在0～30 s内槽内水位场的波动变化主要受前池蓄水高度的影响。各水位计的响应速率随蓄水高度的增大而变快，如在工况4、5和6中，C5达到峰值的时间分别为30.5、25.5和23.5 s，并且C2、C4、C6和C7水位变化规律与C5一致，在溃口洪水演进过程中均呈先增大、后减小的变化趋势；C3的水位变化随着水跃区域的迁移呈先增大、后平缓、再增大、后减小的变化趋势，C3在工况4、5和6的峰值水位分别为4.94、10.46和14.82 cm。

图3 街区流态变化Fig. 3 Flow regime change in the street

图4 街区水位变化Fig. 4 Water level changes in the street

综上所述，溃堤洪水的蓄水高度主要影响街区水位场的峰值水位及响应速率，而前池进口流量主要影响街区水位场在恒定流状态下的水位高度，并且房屋建筑物致使洪水的过流面积减小，导致街区水位沿程呈先增大、后减小的变化趋势。

2.2 有压雨水管网的泄流能力

2.2.1有压雨水管网泄流量

溃堤洪水在街区演进过程中流态复杂多变，并且部分洪水通过有压雨水管网泄流，导致有压雨水管网的水力条件错综复杂。因此，本研究通过布设在雨水管网中的流量计F1～F12用以系统地监测主干管及支管的流量变化，由于流量计F3、F5、F7、F9、F11变化基本相似，部分流量计变化如图5所示。

图5 管网流量变化Fig. 5 Flow changes in the pipe network

溃堤洪水在街区演进过程中，主干管上游F1的流量没有明显波动，支管及主干管下游的流量迅速增大，随后经过小幅度波动后趋于稳定。结合工况3、4、5、6和9可知，当前池蓄水高度相同，进口流量不同时，支管流量在0～5s内迅速增加，并在9 0 s达到稳定，稳定后的支管流量随前池进口流量的增大而增大，如F3的流量在工况3、6和9分别为0.50、0.51和0.52 L/s，而F3、F5、F7、F9和F11所在的支管流量呈先增大、后减小、再增大的变化趋势，如工况9中各支管流量分别为0.52、0.54、0.55、0.54和0.56 L/s。当前池进口流量相同，蓄水高度不同时，各支管的流量计读数随着蓄水高度的减小而滞后，支管流量在0～7 s内迅速增加，并在90 s达到稳定。以工况5为例定量分析管网变化规律：在水跃区域迁移变化的3～9s内，F3一直保持0.82L/s，而其他支管在此期间的流量不足0.5 L/s，且F11在此期间仅有0.19L/s；在水跃区域变化的1 0～1 5 s内，F3流量减小，其它支管流量增大，在20～80 s内逐渐稳定；各支管在90s后的平均流量范围为0.5 1～0.5 6 L/s。

综上所述，前池蓄水高度主要影响支管的最大泄流流量，而前池的进口流量仅对有压雨水管网的泄流量产生了微弱影响。

2.2.2量纲分析法

街区洪水在通过雨水口及其支管下泄至主干管的过程中形成淹没出流，在不考虑街区洪水及主干管的径向流速的条件下，淹没出流公式为：

式中：Q0为支管流量； µ为支管流量系数；A为支管断面面积；h为支管上下游的压差，h=h1-h2，其中，h1为篦前10 cm的水位高度，h2为支管出口处主干管的压力水头；g为当地重力加速度。

结合图3～5可知，各工况在200～300 s内为恒定流。将各工况中重复试验的恒定流数据通过式（2）计算并绘制如图6所示。

图6 支管流量实测值与计算值Fig. 6 Measured and calculated values of branch pipe flow

在不考虑街区洪水及主干管的径向流速的条件下，式（2）的理论计算值与实测数据存在着较大的差异。这是由于支管及主干管汇合处的流量较大所导致的，因此，需要适当地修正管道汇合处的静水头线高度[19]。下文通过引入欧拉数Eu对式（2）进行修正。

结合物理模型试验将影响支管泄流因素表示成一般的函数表达式为：

式中，u1为支管出口处上游的主干管流速，u2为待求解的支管流速， ρ为水的密度。

通过量纲分析的π定理，进一步整理分析支管的泄流能力。将支管流速u2与该支管上游主干管流速u1的比值视为管流比Ru，并结合欧拉数Eu进行拟合，即：

式中：管流比Ru=欧拉数Eu表征压力与惯性力的比值，Eu=其中， ∆p为支管进出口的压差。

管流比（Ru）与欧拉数（Eu）的关系曲线如图7所示。由图7可看出，拟合公式Ru=0.527Eu0.5，相关系数R2=0.97，拟合效果较好。有压雨水管网中支管的泄流公式可表示为：

化简得：

将式（6）的理论计算值同时绘入图6，由图6可知，修正后的淹没出流公式逼近实测数据，平均误差由32%降低至2%。

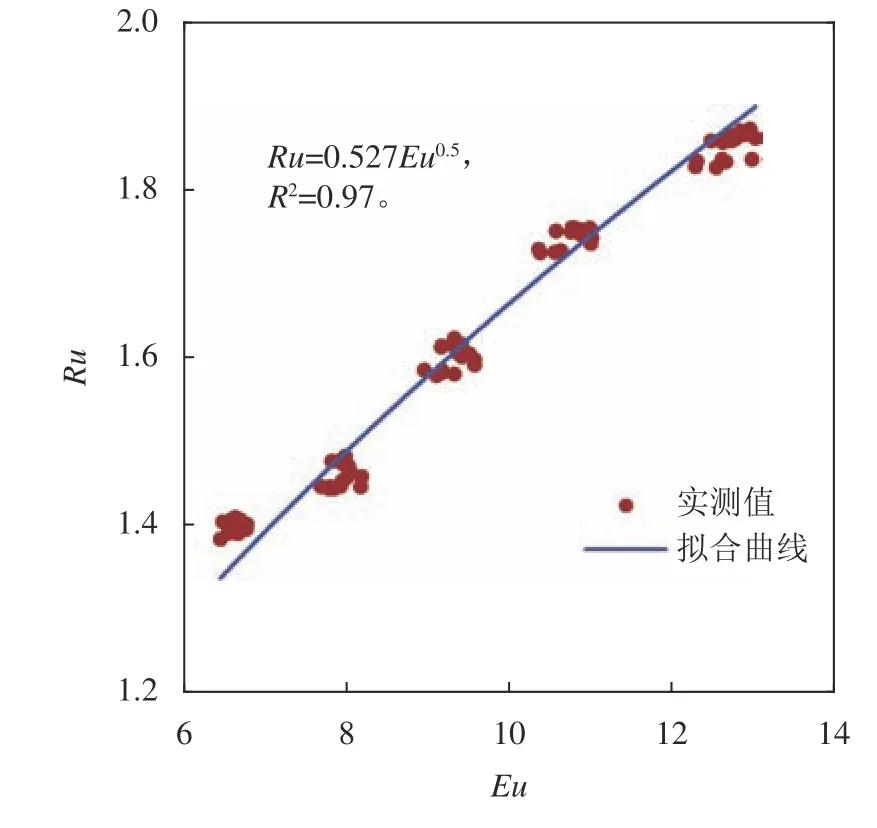
图7 管流比（Ru）与欧拉数（Eu）的关系曲线Fig.7 Relationship between tube flow ratio(Ru)and Euler number(Eu)

3 结 论

本文通过概化水槽模型开展了河堤决口后溃堤洪水在典型城市街区的演进过程，采用超声波水位探针、电磁流量计、压力计系统地测量了街区水位场及雨水管网的关键物理量，研究并分析了不同溃口洪水在有压雨水管网中的泄流量变化，并得出如下结论：

1）溃堤洪水在演进初期，大面积水跃区域在上游街区先由水槽侧壁迁移至道路中心，随后沿道路向街区上游迁移运动，最终向下游迁移直至消失；街区水位在洪水演进后期基本稳定，并且在房屋建筑物的影响下，街区水位从上游至下游水位呈先增大、后减小的变化趋势，水位探针C2～C7的读数在工况6中分别为2.12、2.20、2.21、2.37、2.23和1.76 cm。

2）进口前池的蓄水高度对有压雨水管网内产生较为明显的影响，雨水口S1在洪水演进过程中可达到0.80 L/s的峰值流量。而进口前池的进口流量对雨水口的泄流量影响甚微，各个雨水口在淹没出流条件下，雨水口S2～S4的泄流量基本维持在0.54 L/s，雨水口S1和S5的泄流量分别维持在0.52 L/s和0.56 L/s。3）本研究基于短管淹没出流公式通过引入欧拉数（Eu）综合考虑了雨水主干管流速对支管泄流量的影响，采用支管与主干管管流流速的比值（Ru）与欧拉数（Eu）进行了拟合，并根据拟合曲线对淹没出流公式进行了修正，支管流量Q0=0.527A