基于弹药挂载工作的舰载机保障作业调度

吕晓峰,杨东泽,王丽婷,马 羚

(海军航空大学 岸防兵学院, 山东 烟台 264001)

0 引言

舰载机作为航母编队战斗力的核心,出动架次率将直接影响航母编队的战斗力。舰载机在出动前需进行多项保障作业,其中弹药挂载工作较为复杂,是影响舰载机出动能力的主要因素之一。舰载机出动保障作业流程复杂,并且以上保障作业的进行涉及到多个专业与多种保障设备,各个保障作业之间不仅受到时序约束,同时受到保障设备、保障人员和战位空间等资源约束。因此在对舰载机保障资源合理规划的基础上提高弹药保障能力尤为重要,也是提高舰载机弹药保障能力的迫切需求。

关于舰载机保障作业调度问题,国内外已从不同角度进行了大量分析研究工作。在构建模型方面,苏析超等[1-4]基于舰载机一站式保障模式研究航空保障作业调度优化问题,考虑到设备与人员等约束,在典型任务下运用多种算法求解了调度方案。文献[5-7]从保障作业中会出现扰动事件的角度建立了舰载机保障作业调度模型,运用智能算法求解舰载机甲板作业动态调度问题。文献[8]设计了双种群遗传算法比较不同人机匹配模式下的保障效率与人员负载均衡性,并分析了各个模式的优劣。刘珏等[9]在遗传算法中引入禁忌搜索算子求解了含干扰事件的多机保障问题。张豪等[10]基于随机过程与线性策略建立了舰载机作业流程调度仿真模型,分析了不同调度策略下对舰载机作业安全和出动架次率的影响。但是,上述研究通过不断增加舰载机保障作业约束的复杂度进一步完善模型,未结合弹药挂载工作的特殊性。舰载机弹药挂载需要时间较长,有弹药挂载需求的舰载机通常需要多枚弹药,挂载弹药时会受到众多约束,并且实际进行弹药挂载任务时,航母弹药保障人员会将某一架舰载机的所有弹药集中在一个时间区间内挂载,因此针对弹药挂载工作的特殊性,需要提供一个有利于弹药挂载工作的舰载机保障作业调度方案,通过该方案为弹药挂载工作人员提供便利。

在算法设计方面,舰载机保障作业调度问题本质上属于资源受限项目调度问题(resource constrained project scheduling problem,RCPSP),近年来该问题的主要求解方法大致采用元启发式算法[11]。Mahmud等[12]提出了一种融合3种启发式算法的定制进化算法,更好地修正了不可行解并提高了解的质量。陈浩杰等[13]设计了一种多样性种群更新方式,提出了一种改进超启发式遗传规划算法,提高了算法的搜索能力。Ling等[14]提出一种新的概率模型和更新机制并将其纳入EDA的搜索框架提高了算法搜索能力。同时也有对遗传算法[15-16]、粒子群算法[17]和NSGA-Ⅱ[18]算法进行改进以求解RCPSP问题。其中NSGA-Ⅱ算法被广泛应用于求解多目标优化问题,但该算法也存在易于早熟、解集多样性不足等问题。

针对以上不足,结合舰载机弹药挂载的实际情况,在舰载机多机一体化联合保障模式下建立了考虑弹药挂载工作下的舰载机保障作业调度模型,提出了一种新的染色体片段的编码方式以及相应的交叉和变异操作,结合经典的NSGA-Ⅱ算法提出一种改进的NSGA-Ⅱ算法[19]。

1 问题描述

舰载机一体化联合保障是指舰载机在满足单机保障流程约束的条件下,合理调度人员与设备等保障资源,更加高效地完成舰载机保障作业,提高舰载机出动效率,同时在保障过程中,舰载机不需要往返转运,只需在固定的停机位进行保障,保障资源在不同的舰载机战位之间转换保障。舰载机在固定停机位进行保障作业时合理地调度保障资源尤为重要,因此制定符合实际约束与高效的保障资源调度方案是执行舰载机出动保障任务的关键。舰载机在进行保障作业时所受到的资源约束主要可将其分为保障流程约束、保障人员约束、保障设备约束、供给性资源约束与保障空间约束。

1) 保障流程约束。舰载机在进行保障作业时需受到单机保障流程约束,各个工序需满足紧前工序和紧后工序约束关系。如图1所示为多机保障网络图[1],图中Oij表示第i架舰载机正在进行第j道保障工序,S和E为虚拟工序,不进行实质工作且不消耗资源,分别表示起始节点与结束节点,Si和Ei为第i架舰载机的虚拟起始工序和虚拟结束工序。

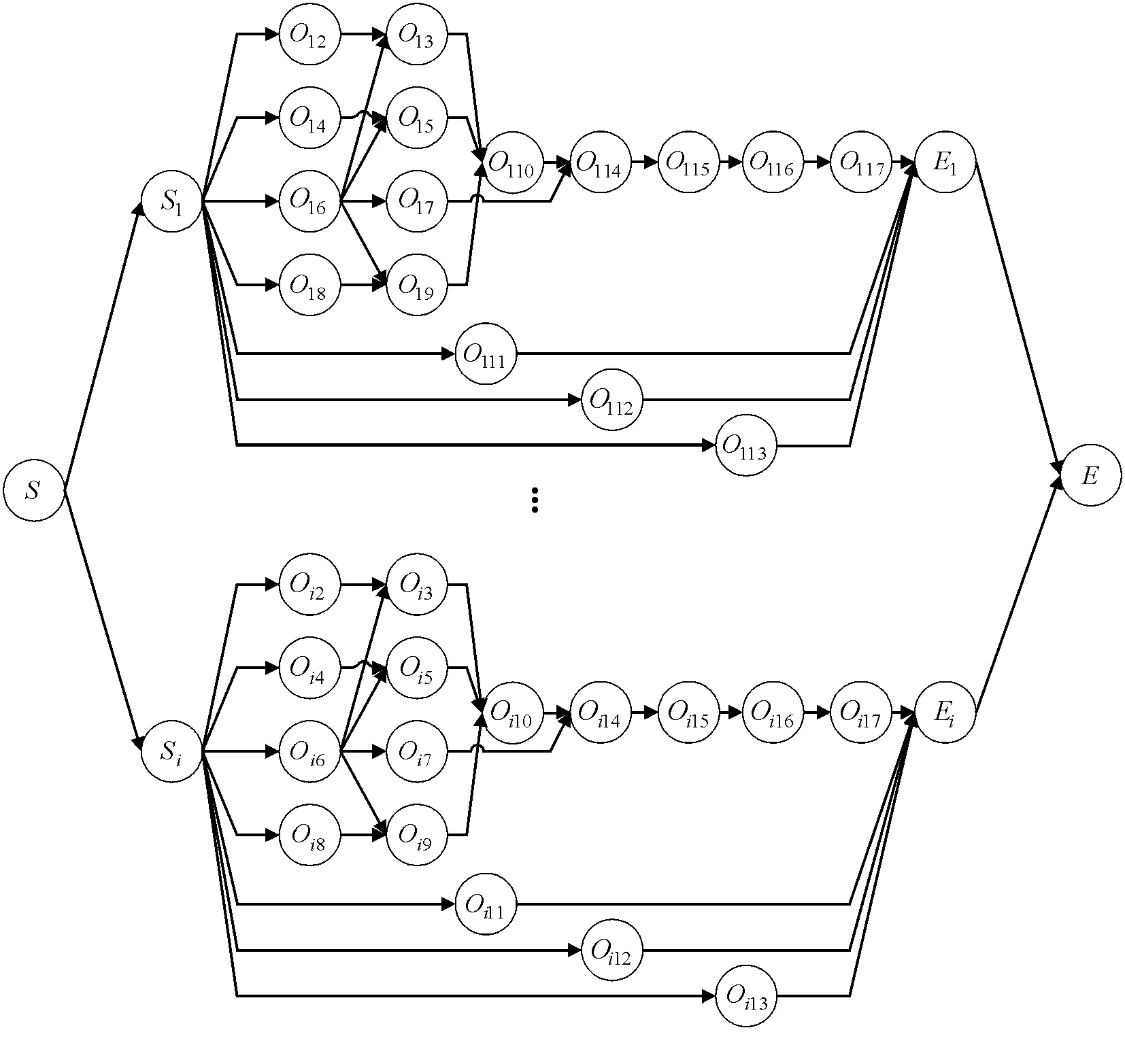
图1 多机保障网络图

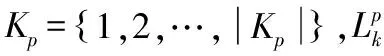
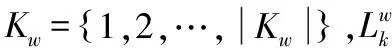
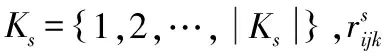
2 弹药挂载下的舰载机保障作业调度模型建立

2.1 调度模型参数定义

调度模型中各参数定义如下:

I={1,2,…,n}表示需保障的舰载机集合,n为舰载机数量;

Ji={1,2,…,|Ji|}为第i架舰载机的工序集,|Ji|为第i架舰载机的工序数;

Sij为工序Oij保障起始时间;

Tij为工序Oij保障所需时间;

Eij为工序Oij保障结束时间;

Cmax为舰载机最大保障结束时间;

Vek和Vpk分别为舰载机保障人员和保障设备的负载方差;

Pij为工序Oij的紧前工序集;

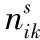
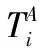
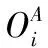
决策变量定义为:

2.2 模型建立

为了使得到的调度方案更加合理可行,在优化目标方面构建了舰载机保障作业完成时间和负载方差最小化的多目标优化模型,即

F1=minCmax

F2=min(Vek+Vpk)

(1)

式(1)中

(2)

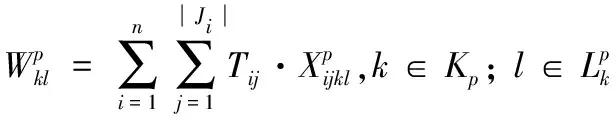
(3)

约束条件为

Eij=Sij+Tij, ∀i∈I, ∀j∈Ji

(4)

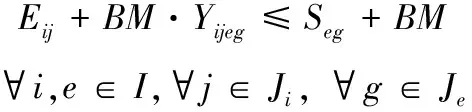
(5)

Sij≥Sih+Tih, ∀h∈Pij,∀i∈I,∀j∈Ji

(6)

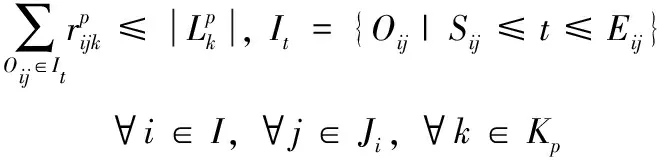
(7)

(8)

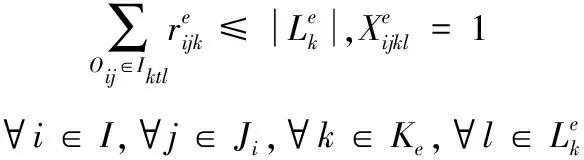
(9)

(10)

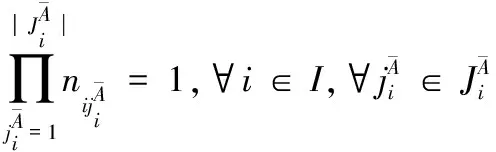
(11)

其中,式(1)为模型的目标函数;式(4)表示工序Oij的保障起始时间与结束时间的关系;式(5)表示不同工序分配至相同的保障设备或人员时按照优先级有序保障;式(6)表示同一舰载机的不同工序需满足紧前关系约束;式(7)表示工序Oij保障期间所需的该类人员需求量需小于其数量上限;式(8)表示同一舰载机的战位空间不能超过其可容纳的人员数量;式(9)表示工序Oij保障期间所需的该类设备需求量需小于其数量上限;式(10)表示工序Oij保障期间所需的该类供给性资源需求量需小于其可同时供给的数量上限;式(11)表示在进行弹药挂载时不能与其冲突的工序同时保障。

3 改进型NSGA-Ⅱ算法设计

NSGA-Ⅱ算法是基于Pareto最优解的多目标优化算法,通过对种群进行快速非支配排序以达到对种群的分级,在求解多目标问题中已被广泛应用[20-21]。NSGA-Ⅱ算法通过对种群进行快速非支配排序达到对种群的分级,计算种群个体的拥挤度来保持种群的多样性,以得到较优解[22]。

3.1 编码与解码

RCPSP问题中个体的编码方式主要包括任务列表编码、优先数编码以及优先规则(优先权)编码,其中任务列表编码性能通常会优于其他编码方式[23],并且操作简单、易于实现,因此具有较为广泛的应用。但是在保障对象与保障工序较多的情况下,随机生成的任务列表编码很难满足各个工序之间的紧前紧后约束关系,为了进一步提高算法的效率,在编码时结合工序间的紧前紧后约束关系分片段生成染色体。

根据任务列表编码方式,生成的染色体维度为num=∑|Ji|,其中根据各个工序的优先级分片段生成染色体。首先将虚拟起始放置在片段1,其次按照优先级将其紧后工序安置在片段2中,依次类推,完成染色体的编码,如图2所示。其中xk为一个小数,整数部分表示舰载机序号,小数部分表示工序号。

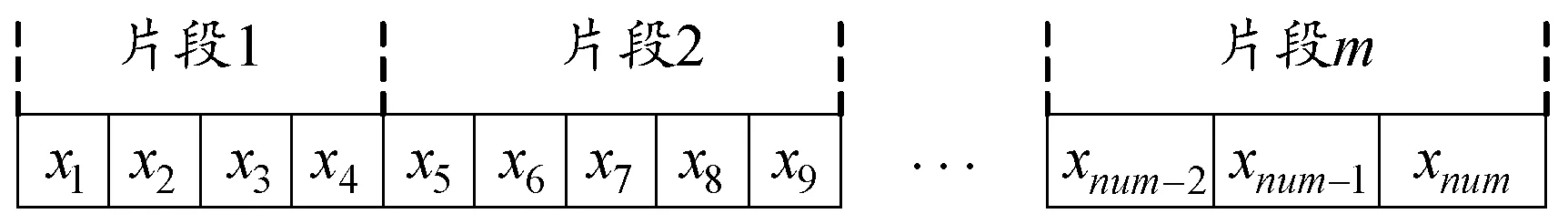
图2 染色体编码示意图

解码操作是根据染色体的编码转化成可执行的调度方案,结合当前资源分配现状,在满足资源约束的条件下根据染色体编码方案将各个工序安排至最早可能开始的时间,为了完成上述操作,采用了串行调度机制(SSGS)[24]进行解码。

3.2 快速非支配排序

NSGA-Ⅱ中的快速非支配排序是根据个体的支配关系对种群进行分级,其作用是指引搜索向Pareto最优解集方向进行,使种群向最优解集方向进化,并根据个体拥挤度在相同层级的个体内进行选择性排序。通过循环遍历所有个体,并比较个体间的适应度值确定其支配关系,即支配关系代表了解的优劣程度,经过多轮排序,最终得到种群个体的非支配层次关系。令p为当前个体,q为与个体p比较的其他个体,P为当前种群,np为当前个体被其他个体支配的数量,Sp为受个体p支配的个体集合,Fi为第i级非支配解集,Q为存放下一层级的非支配解的集合。实现流程如下:

for eachp∈P

Sp=∅

np=0

for eachq∈P

if (pq) then 如果p支配q

Sp=SP∪{q} 将q添加到个体p的支配

else if (qp) then 集合SP中

np=np+1 支配p的个体个数递增

ifnp=0 thenp属于第一层级

prank=1

F1=F1∪{p}

i=1 初始化层级数

whileFi≠∅

Q=∅ 集合Q用于存储下一

for eachp∈Fi层级的个体

for eachq∈Sp

nq=nq-1

ifnq=0 then 个体q属于下一层级的非支配解

qrank=i+1

Q=Q∪{q}

i=i+1

Fi=Q

根据以上步骤可将种群进行分层,对于同一层级内的个体通过拥挤距离进行区分,优先选择拥挤距离较大的个体,可以使相似度较低的解保存下来,可形成分配比较均匀的Pareto前沿[25]。

3.3 交叉操作

算法设计中的交叉方式主要包括单点交叉、多点交叉和部分匹配交叉等[26],在进行上述交叉操作时,染色体的编码会发生变化,破坏染色体编码中的前后约束关系,在进行交叉操作之后需判断是否满足约束关系,若不满足需进行调整。因此考虑到工序之间的紧前紧后约束关系,并结合染色体的编码方式提出了基于染色体片段的交叉方式,将编码中的片段视为一个整体,可缩小交叉位置的范围,并避免了不可行解的发生,提高了算法的搜索速度,图3为染色体的交叉操作示意图[15]。其中染色体内的数值仅供交叉操作的演示,与实际染色体的数值无关,具体操作方法如下:

Step 1:令交叉概率为p1,随机生成α(0≤α≤1),设参加交叉操作的2个父代个体分别为A1和A2。若α≥p1则进行下一步骤,否则直接进行变异操作。

Step 2:生成片段选择参数b(b∈[1,nm]),nm为染色体片段个数,通过参数b确定染色体的交叉点pos1。

Step 3:将A1的前pos1个片段与A2的后nm-pos1个片段进行组合形成子代个体B1,同时将A2的前pos1个片段与A1的后nm-pos1个片段进行组合形成子代个体B2。

图3 染色体交叉操作示意图

3.4 变异操作

种群通过变异操作对染色体的局部基因值做变动获得新的个体,增加了种群的多样性。传统的变异操作是一种盲目的、随机的变异过程,主要有“基于位置的变异”和“基于次序的变异”,其中基于位置的变异操作是在染色体中随机生成2个变异位,并将后续的基因直接插入到第一个变异位置之前,基于次序的变异操作同样在染色体中随机生成2个变异位,并将2个变异位的基因进行交换,若不满足紧前约束关系,则需停止此次操作,转入下次交换。上述变异操作的随机性较大,不能够保证每次变异之后染色体的质量,需要设计一个能够判断变异之后的染色体是否满足紧前紧后约束关系并进行修正的机制,增加了算法的复杂度,因此本文设计了基于染色体片段的变异操作,图4为染色体的变异操作示意图,具体操作方法如下:

Step 1:令变异概率为p2,随机生成β(0≤β≤1)。若β≥p1则进行下一步骤,否则跳过变异操作。

Step 2:生成片段选择参数d(d∈[1,nm]),nm为染色体片段个数,通过参数d确定染色体的变异片段位置,并随机生成变异点pos1和pos2,其中需小于该片段中的基因数。

Step 3:在染色体片段d中交换变异点pos1和pos2两处的基因。

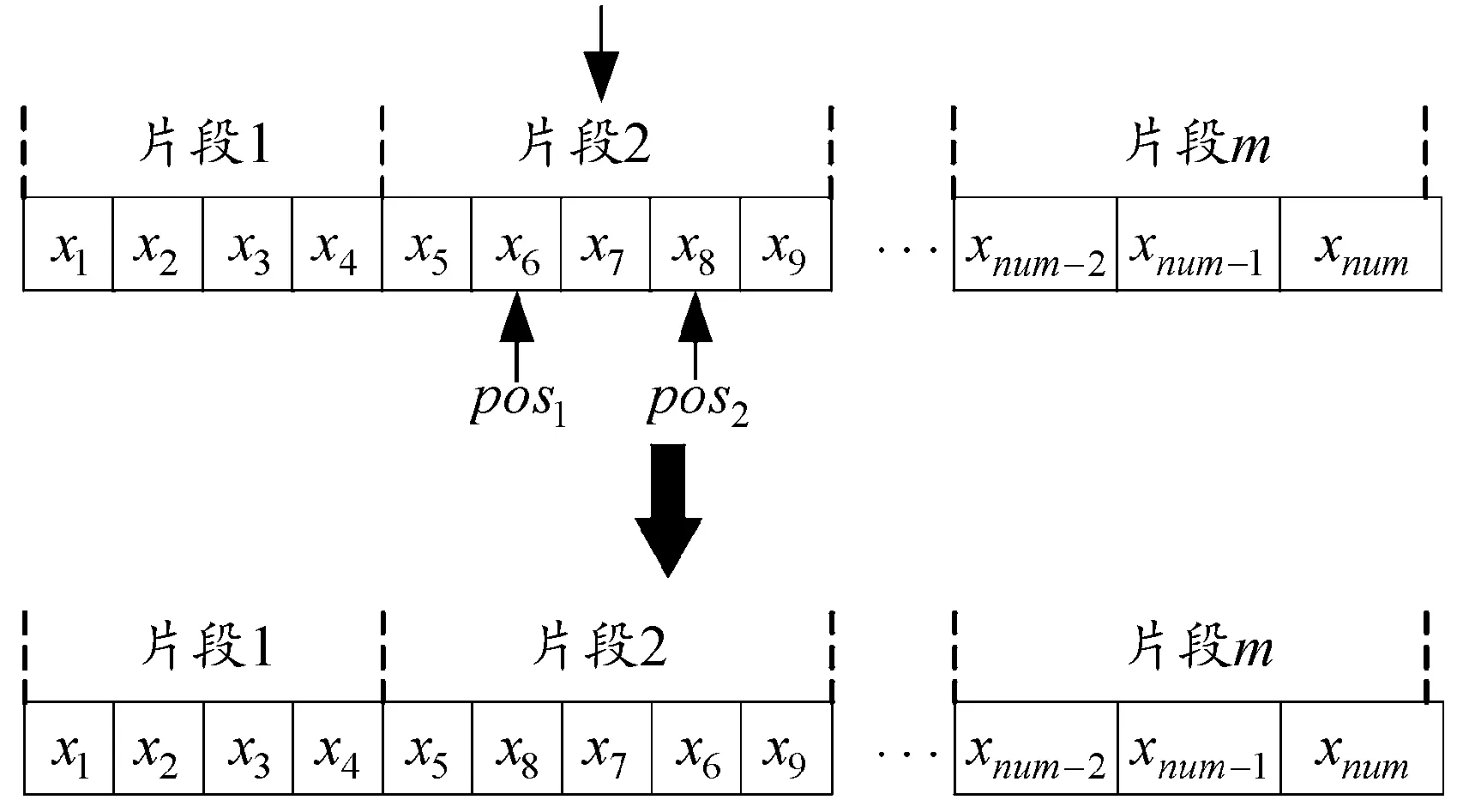
图4 染色体变异操作示意图

3.5 最优调度方案选择

由于舰载机保障作业完成时间与保障资源负载最小化2个优化目标之间可能存在对立关系,在多目标优化问题中并不存在某种单一的最优解决方案[27],Pareto前沿的各个调度方案之间互不支配,需要针对研究问题从多个调度方案中选择适合该问题的最优调度方案。从Pareto前沿的多个调度方案选择最优的方案通常采用的方法是加权求和法,该方法常用于作业调度多目标优化问题。定义权衡适应度值为

F=ω1F1+ω2λF2

(12)

式(12)中:ω1、ω2分别为对应目标函数值的权重系数;λ为平衡系数。

求解多目标优化问题时,不同目标其侧重点不同,通过赋予各个目标不同的权重系数来选择最优方案。针对本文中研究的问题,负载方差和保障作业完成时间相差一到2个数量级,需要根据实际数值设置平衡系数,否则数量级小的目标函数对权衡适应度值的影响很小。舰载机保障作业中需优先保证作业完成时间,故将权重系数取为相对大值。

3.6 算法流程

本文中提出的算法流程如图5所示[15]。

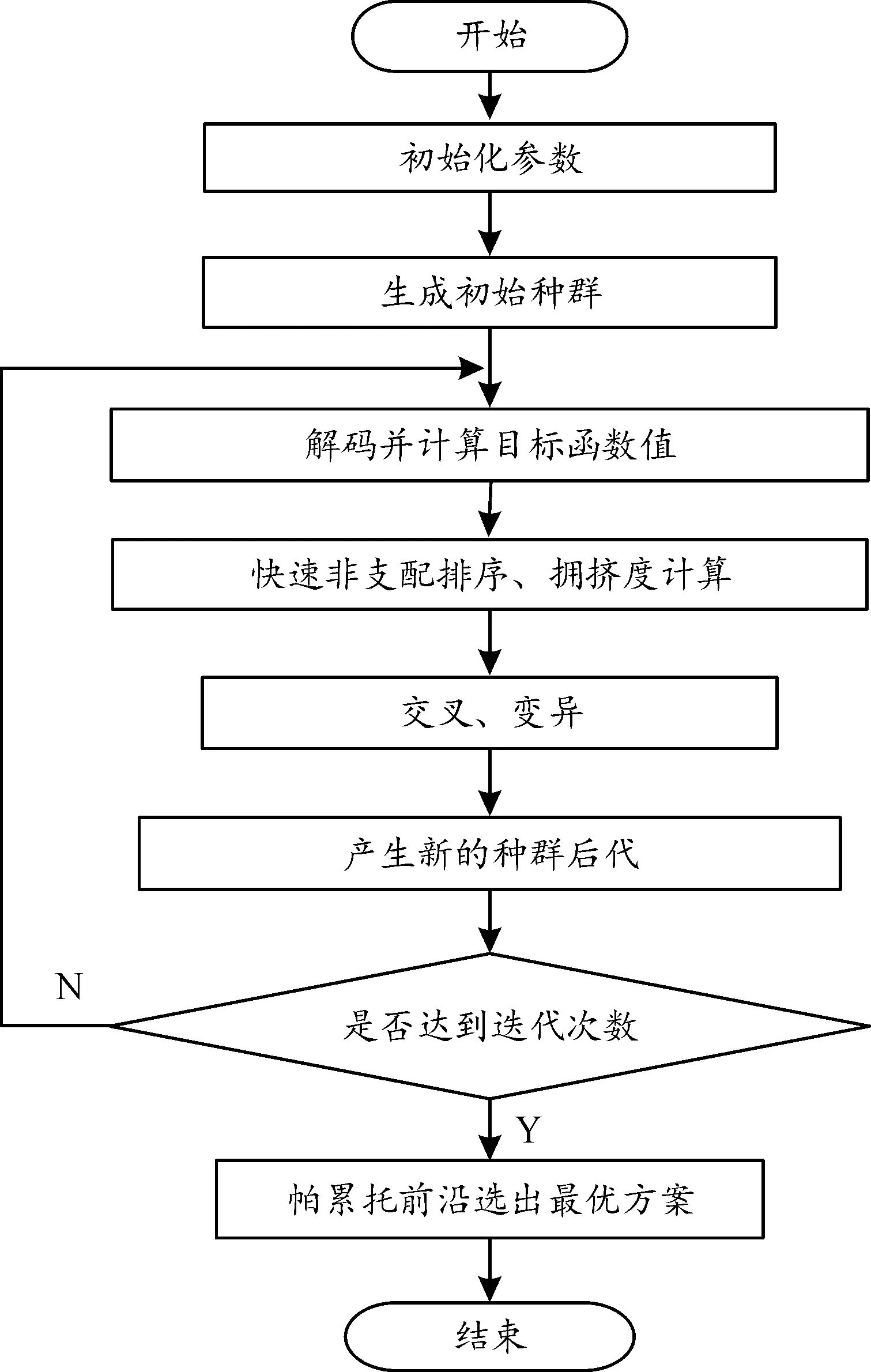
图5 算法流程图

具体的操作步骤如下:

Step 1:设置算法基本参数:种群数量、迭代次数、交叉率和变异率,并根据本文设计的编码方式进行染色体编码。

Step 2:对种群快速非支配排序并计算拥挤度。

Step 3:按照本文中设计的交叉和变异操作对种群进行迭代更新。

Step 4:若达到算法终止条件则输出种群中的最优方案,否则转至Step 2。

4 仿真分析

本文中的舰面保障作业调度以国外某型航母为例,典型任务为6架舰载机同时进行出动前的保障作业,并假设在保障过程中所有参与保障的舰载机不发生故障,舰载机的出动保障作业流程如图1所示。图中工序15为舰载机弹药挂载工序,每架舰载机的弹药挂载时间长度为30 min,针对此次保障的舰载机其各工序对各类资源的需求如表1所示[28]。各个工序的所需时长如表2所示。

表1 保障工序资源需求

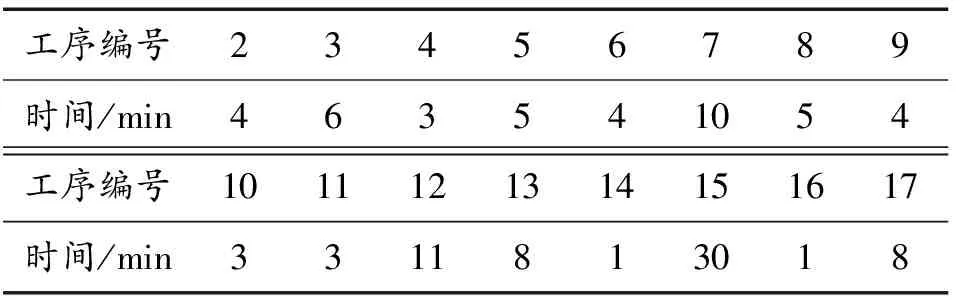
表2 保障工序所需时长

上述前5种保障设备均为固定设备,无法覆盖到全部机位,惯导对准装置相较于其他保障设备较为充足,不会对舰载机的出动保障作业造成约束,表3表示各个保障设备对各个机位的覆盖情况。

对于改进的NSGA-Ⅱ算法种群数量设置为Pop=100,算法迭代次数设置为cg=100,交叉率设置为p1=0.8,变异概率设置为p2=0.2,保障作业完成时间权重设置为ω1=0.7,负载方差权重设置为ω2=0.7,平衡系数为λ=50,在相同的参数设置下选取文献[29]中的NSGA-Ⅱ算法与本文设计的改进NSGA-Ⅱ算法进行对比,运用Matlab软件进行仿真,图6为改进NSGA-Ⅱ与NSGA-Ⅱ得到的非支配解对比图[21]。图7为改进NSGA-Ⅱ与NSGA-Ⅱ的迭代过程图[25]。

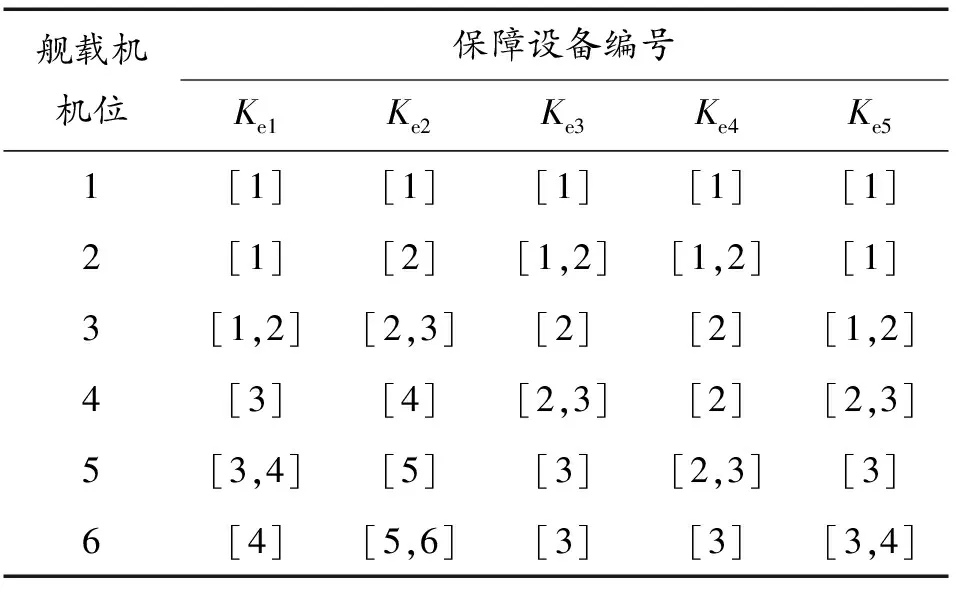
表3 保障设备对各个机位的覆盖情况

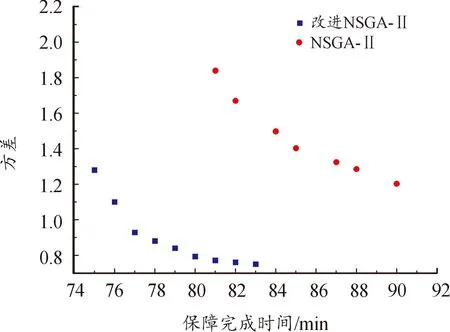
图6 改进NSGA-Ⅱ与NSGA-Ⅱ所得的非支配解

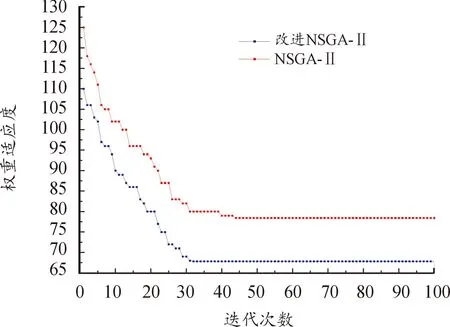
图7 改进NSGA-Ⅱ与NSGA-Ⅱ迭代过程图

图6和图7中改进NSGA-Ⅱ算法和NSGA-Ⅱ蓝色的符号与线条表示改进NSGA-Ⅱ算法的仿真结果,红色的符号与线条表示NSGA-Ⅱ的仿真结果。根据图6可看出改进的NSGA-Ⅱ算法非支配解集性能更优,NSGA-Ⅱ算法生成的解全部被改进的NSGA-Ⅱ生成的解支配。根据图7可看出改进的NSGA-Ⅱ算法收敛速度更快,全局搜索能力更强,其在迭代至32代时求得最优权重适应度值67.85,而NSGA-Ⅱ算法在迭代至44代时求得权重适应度值78.445,并陷入了局部最优解。通过2种算法比较,改进后的算法收敛速度提升了23%,最优解提升了16%。

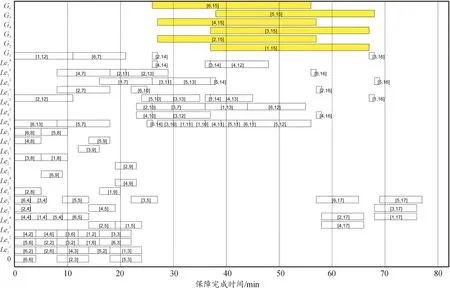
图8 保障人员调度甘特图

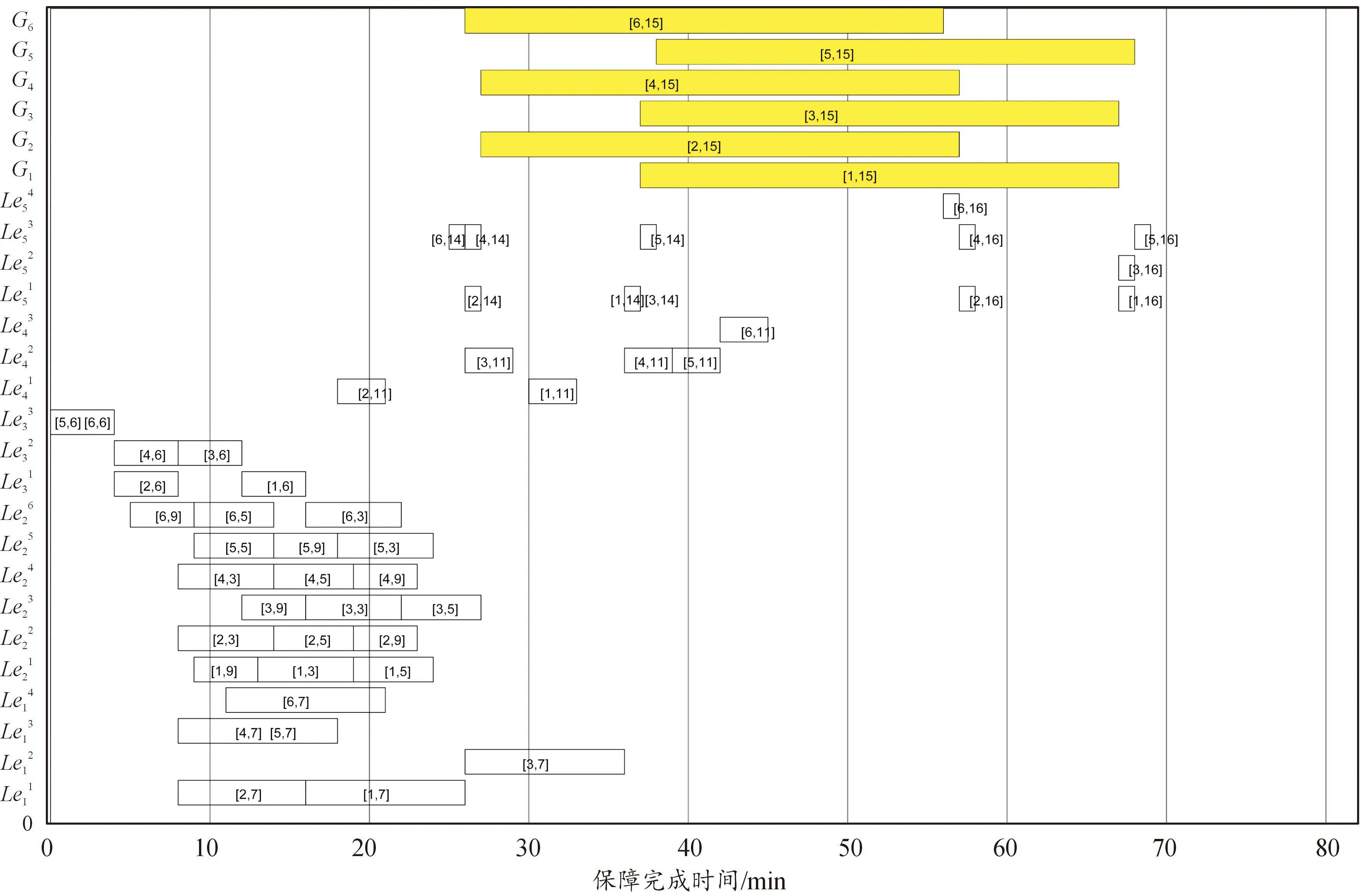
图9 保障设备调度甘特图

图10 6架舰载机优化调度方案甘特图

5 结论

本文中建立了弹药挂载工作下的舰载机保障作业调度模型,提出了一种改进的NSGA-Ⅱ算法,对舰载机保障资源进行合理调度,得到主要结论如下:

1) 对舰载机的弹药挂载调度与其他出动保障作业进行区分考虑,将每架舰载机的弹药挂载时间安排为一个时间区间,建立了舰载机保障作业调度模型。

2) 提出了基于工序优先级的染色体片段编码,并在此基础上对NSGA-Ⅱ算法的交叉与变异操作提出改进。

3) 对设计的模型与算法进行仿真,结果表明,舰载机弹药挂载工作更加切合实际,降低了舰载机保障作业的复杂度,算法收敛速度提升了23%,最优解提升了16%。