结合AHP和BN的桥梁桩基破坏评估模型构建及应用
李向玉
(贵州顺康检测股份有限公司,贵州 贵阳 550000)
桥梁桩基是桥梁建设中不可或缺的一部分,它们是构成桥梁框架的重要基础结构,负责桥梁的承载、抗震、抗滑、抗拉等功能。然而,由于桩基受到外力的影响,桩基的破坏是大多数桥梁结构的主要破坏模式,直接影响桥梁的安全性和稳定性[1-2]。因此,研究和开发准确高效的桥梁桩基破坏评估模型是保证桥梁安全稳定性的现实需求。许方安等[3]通过理论分析和现场试验,分析了水利工程基坑开挖对临近桥梁桩基的影响,并提出了相应的防治措施。李炼[4]通过实地测量,研究了桩基施工对高铁隧道的影响情况,利用有限元法建立了施工时的结构受力模型,以确保施工的安全、可靠和高效。胡潇等[5]对桥梁桩基施工质量控制措施进行了分析,提出了一系列有效的方法,来保证桥梁施工质量。基于批量归一化(Batch Normalization,BN)的桥梁桩基破坏评估模型应用及研究,将应用层次分析法(Analytic Hierarchy Process,AHP)结合批量归一化对研究所确立的桥梁桩基破坏评估指标进行分析,并针对不同地质条件,建立对应的桥梁桩基破坏模型,以实现桩基损伤系数的精确评估。该评估模型应用于桥梁桩基破坏评估,能够帮助工程师更好地了解桩基破坏的原因和影响因素,从而更好地采取预防措施。此外,此次研究的新颖性在于采用层次分析法和贝叶斯网络相结合的方法构建新型评估模型,将定性和定量相结合,可以更准确地评估桩基破坏的风险,并可以为工程师提供预防桩基破坏的建议和措施。
1 工程概况及桩基病害检测方法与模型构建
1.1 工程概况及试验探测方法
新星大桥位于龙惠高速段的丘陵区,中部为丘间谷地,主要为鱼塘、水库;两侧桥台附近为丘陵低山,山体高大、山坡较陡。桥址两端位于山坡上,山坡较陡,植被发育,场区有乡村土路与外界相通,交通条件较差。桥位区地面标高约33.5~89.6 m。场区地貌上属于丘陵地貌单元区。结合桥位处地形、地质和场地条件等特点,考虑工程的安全性、经济性、施工可行性、景观性要求,桥型方案左幅上部结构采用(3×35+5×20+5×20+5×20+4×20+4×20+4×20+1×20)m预应力混凝土先简支后连续小箱梁,折合整幅桥长671.1 m。桥跨起点桩号为K44+156.4,终点桩号为K44+827.5,中心桩号为K44+492.5;右幅上部结构采用(3×35+3×20)m预应力混凝土先简支后连续小箱梁,折合整幅桥长177.2 m。下部桥墩采用圆柱墩;桥台采用圆柱台及肋板台,伸缩缝均采用80型。本桥平面分别位于圆曲线(起始桩号:K44+156.36,终止桩号:K44+371.286,半径:1 530 m,右偏)、缓和曲线(起始桩号:K44+371.286,终止桩号:K44+621.286,参数A:618.466,右偏)和直线(起始桩号:K44+621.286,终止桩号:K44+827.54)上,纵断面位于R=25 000 m的竖曲线上;墩台径向设置。桥梁交角为90°,桥台背墙前侧线、桥墩中心线与道路设计线的右偏角为90°。因为此次检测所处地区的水深并不是很深,而且在水中的能见度也比较高,在对经济效益和检测的可用性进行了全面的考量之后,此次检测最终采用了一种可以进行河底探摸和水下拍照的检测方式[5-7]。
该试验探测采用40台摄像机构成河底构造表面观察系统,它能够迅速地获取到河底探测的影像,与常规的河底拍摄系统相比较,它显著地提升了对探测数据进行分析和处理的效率,而且具有很好的现场适应能力,对测试技术的需求也不高,适用于这次的测试。桩基础冲刷测深点的布置采用固定的径向网格模式,测深点之间间距≤1 m,桩基础冲刷测深点总数为128点;桩基础桩孔护筒测深点布置采用双螺旋线形布置,测深点之间间距≤1 m,桩基础桩孔护筒测深点总数为128点。本次检测除了上述的河底探摸和水下拍照检测外,还采用了X射线照相检测和河底钢筋检查技术,以保证桥梁构件的安全性。针对桥梁构件,采用X射线照相技术,可以清楚地看到构件内部的结构,从而有效排查构件的缺陷。而河底钢筋检查则可以准确地检测出桥梁构件的钢筋混凝土强度,以及构件的锈蚀情况,以确保桥梁的安全性。测点分布如图1所示。

图1 桩基础冲刷测点布置方式
由图1可知,桩基础冲刷测深点的布置,为固定的径向网格模式,测深点之间间距≤1 m。其在3点钟、6点钟、9点钟以及12点钟四个方向分别均匀排布有6个桩基础冲刷测点。
1.2 水下桩基病害损伤评估模型构建
为了更好地对新星大桥的桩基病害进行准确评估,研究提出构建新型的桩基病害损伤评估模型并进行评价。在进行特定的数学模型构建前,通常要对原始数据进行一个规范化处理(Normalization),然后将规范化的数据用于模型构建和分析。研究选取的标准化方法为批量归一化(Batch Normalization,BN)。这是由Google在2015年提出的一种算法,用于解决深度神经网络中的梯度消失/爆炸问题,以及在数据建模时对大批量的数据进行归一化处理,并加速网络的训练过程。BN的主要思想是在每一层的输入数据上执行归一化操作,使其落入一个稳定的分布中,从而消除参数之间的依赖关系,从而加速网络的训练过程。BN表达式如公式(1)所示。
(1)
式中:x为输入数据;mean为批次数据平均值;std为样本方差;gamma为缩放比例;beta为平移参数。
在对数据进行归一化处理后,选用层次分析法(Analytic Hierarchy Process,AHP)对大桥水下桩基病害损伤进行评估。层次分析法是一种以定性和定量为基础的多目标决策分析方法,将与决策有关的因素分解为目标、准则、方案等层次,实现了对决策的定量化。层次分析法是根据两个反差系数的相关性来构造B类判断矩阵,并确定两者间的相关性。
利用B的属性对矩阵进行计算,判定其相容性,该方法的具体实现方法为利用和积法对各个列的因素进行规范化处理,得出各因子的一般项如公式(2)所示。
b1=b2/∑bn
(2)
式中:bn为第n个因素,b1、b2为第一个因素和第二个因素,∑bn为第一个因素和第二个因素之间的总和。
利用B类判断矩阵,根据计算结果,评价各因素的相关性,判断决策的可行性。层次分析法有助于提高工程决策的效率,能够找出最优解,有助于把握复杂问题的发展趋势,提高决策的科学性和质量。大桥水下桩基病害损伤评估指标,具体如表1所示。
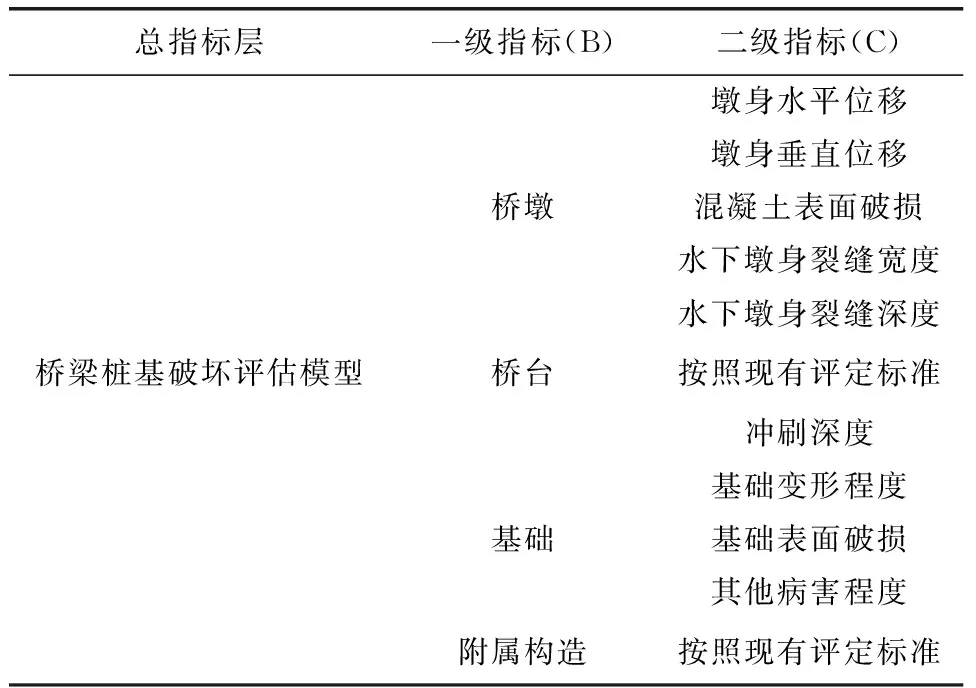
表1 桥梁桩基破坏综合评价体系架构
表1列出了桥梁桩基病害损伤评估指标的框架,包括4个一级指标和9个二级指标,其中桥墩、桥台、基础和附属构造分别包括5、1、4和1个二级指标。判断矩阵的数值是对每个评估因素的相对重要性最直观的反映,数值的大小尺度及对重要性的响应如表2所示。

表2 矩阵判定标度及其含义
表2中的矩阵判定标度表示不同评估因素之间的相对重要性。
2 基于批量归一化和层次分析法的桥梁桩基破坏评估应用效果分析
针对新星大桥桥梁桩基破坏评估进行应用效果分析,采用基于批量归一化和层次分析法,对桥梁桩基破坏评估进行深入研究。选取80组桥梁数值做评估研究。在归一化步骤中,选取冲刷深度h来进行归一化效果的评估。
如图2所示,将冲刷深度h数据矩阵进行归一化处理后得到数据柱状图,从图中可知,经过归一化处理后的数据,均在[0,1]之间分布,且其排布层次感更加鲜明,经过预处理后的数据矩阵,不但去除了数据中的白噪声,而且将高斯白噪声剔除,使其接近于无干扰状态。因此,基于批量归一化和层次分析法的桥梁桩基破坏评估应用效果较好,评估精度高,可靠性强;批量归一化技术可以消除原始数据中的影响因素,有效控制评估结果的变异性,提高评估精度。利用MATLAB分别建立不同类型的评估模型,并由10名专家对不同级别的评估因子进行对比,得出不同级别的评估结果,计算出不同级别的判定矩阵的最大特征值与最大特征根之间的正规化矢量,并验证判定矩阵的相容性。具体如表3所示。
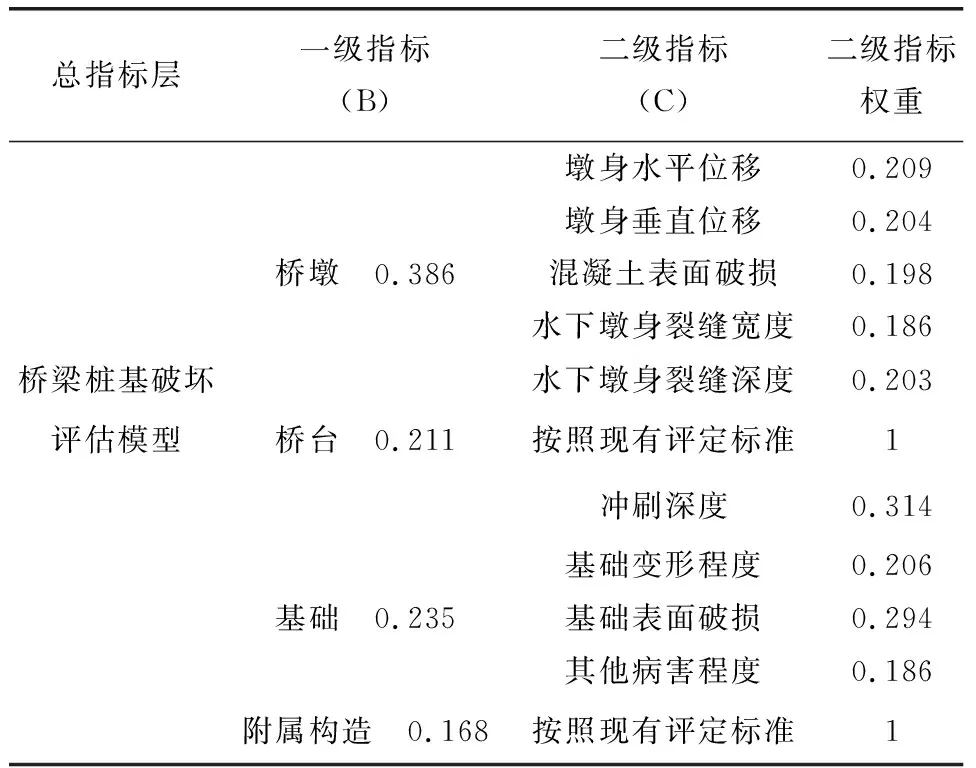
表3 指标层权重结构表
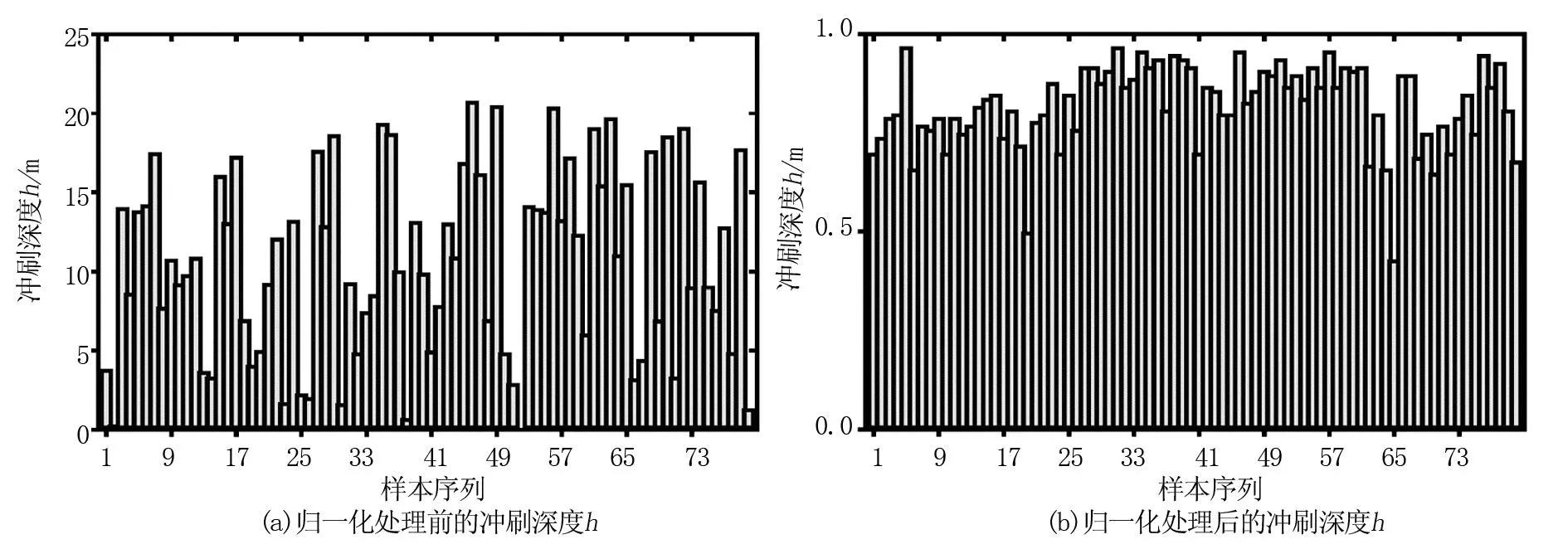
图2 冲刷深度h进行归一化处理前后效果对比
表3显示了桥梁桩基破坏评估模型的指标层权重结构。从总指标层上看,桥墩占有最大的比重,占总比重的38.6%,其次是桥台占21.1%,基础占23.5%,附属构造占16.8%。在一级指标层上,墩身水平位移、墩身垂直位移、混凝土表面破损、水下墩身裂缝宽度和水下墩身裂缝深度的权重分别为20.9%、20.4%、19.8%、18.6%和20.3%;在基础一级指标层上,冲刷深度、基础变形程度、基础表面破损和其他病害程度的权重分别为31.4%、20.6%、29.4%和18.6%。以标准层次为基础,可以求出最优化的综合权值。在二级指标层上,按照现有的评定标准,桥台和附属构造的权重均为1。经过计算后,随机一致性比率CR2=0.0292<0.1,表明一致性测试通过,接受所求得的比较矩阵与权值系数。因此,桥梁桩基破坏评估模型的指标层权重结构完整、清晰,为桥梁破坏评估模型提供了有力的支持。基于上述指标层权重结构,可以求出桥梁桩基破坏评估模型的综合权值。根据现有的评价标准,在每个一级指标层上,可以计算出最优化的综合权值。这样,就能够得出桥梁桩基破坏的综合评价,为桥梁的管理和维修提供有效的参考。为了进一步探究桥梁桩基在河水冲刷时的稳定性,选取不同水位、不同渗透率以及不同水位下降速率来对桥梁桩基的稳定性进行分析,如图3所示。
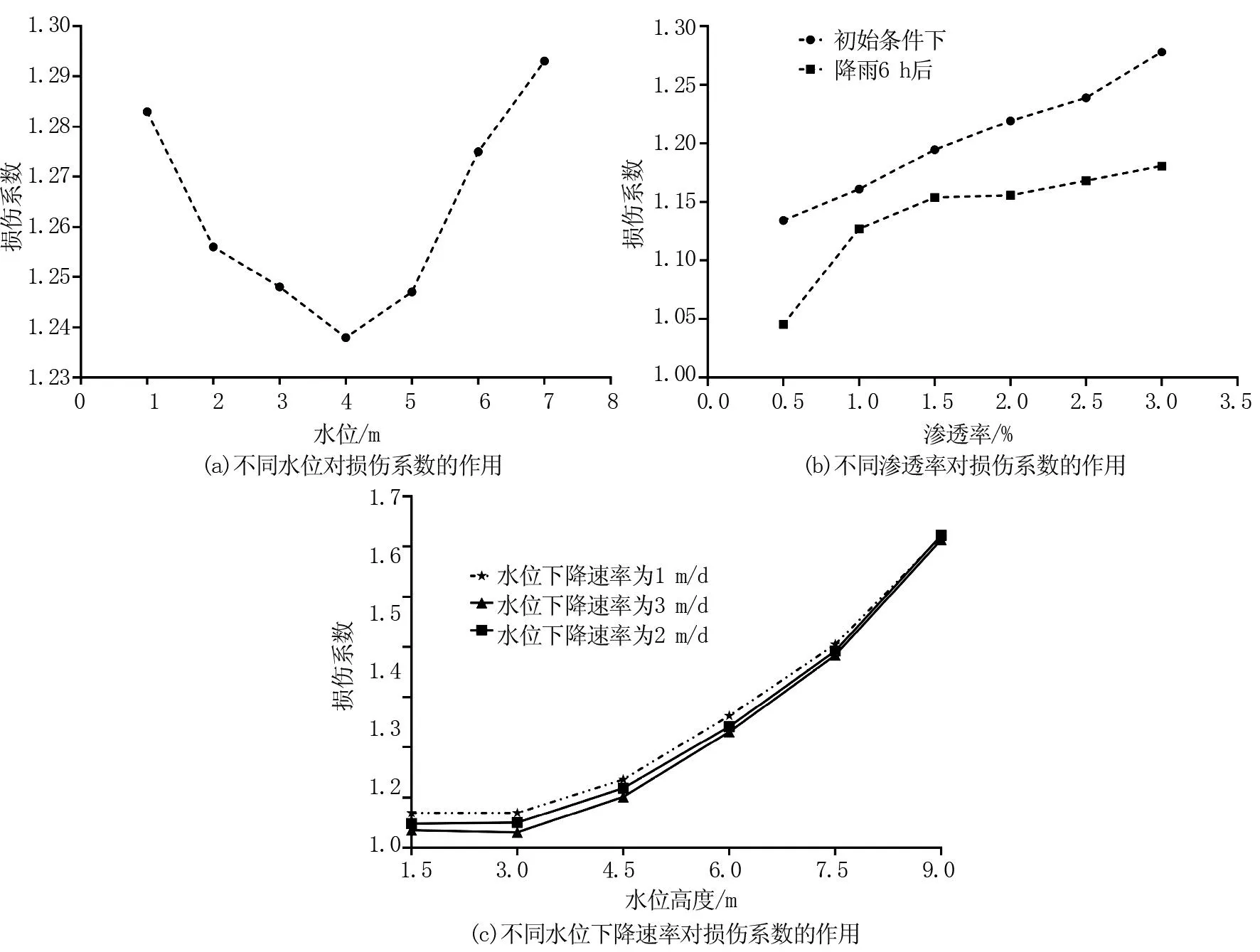
图3 不同影响因子条件下对桥梁桩基损伤系数的影响程度
由图3(a)可知,随着水位的增加,桥梁桩基的损伤系数由降低到增加,当水位高度为1~4 m时,损失系数由1.285下降为1.238; 当水位高度为4~7 m时,损失系数由1.238上升至1.296。由图3(b)可知,初始条件下,桥梁桩基的损伤系数随着渗透率的增加而增加,且其损失系数由0.5%渗透率时的1.138上升至3.0%渗透率时的1.289。经过6个小时的强降雨,会导致桥梁桩基的损伤系数的降低。所以在水平方向渗流系数低于竖直方向时,降水对桥梁桩基的影响更大。由图3(c)可知,水位高度在6 m以下时,不论水位下降速率维持在哪种水平,其损伤系数并未发生太大变化。初始损伤系数为1.0~1.2,若水位>6 m时,其斜率出现了骤增的现象,损伤系数骤升至1.5~1.7。当水位升到9 m 时,桥梁桩基的损伤系数已经达到1.67。在桥梁桩基破坏评估中,渗透率、水位及水位下降速率均为重要的影响因素。
3 结 论
以新星大桥为例,对构建的新型桩基损坏评估模型在实际中的应用进行了分析。经过计算,随机一致性比率CR2=0.0292<0.1,证明一致性测试符合要求,接受所求得的比较矩阵与权值系数。因此,桥梁桩基破坏评估模型的指标层权重结构完整、清晰。此外,通过实证分析还发现,在桥梁桩基破坏评估中,渗透率、水位及水位下降速率均为重要的影响因素。

