圆柱共形阵低副瓣波束形成算法研究

刘海波 韩宇新 武兴恺 陈广茂

（1.北京理工大学信息与电子学院，北京 100081；2.北京理工大学信息与电子学院CEMEE国家重点实验室电磁感知研究中心，北京 100081）

1 引言

相比于传统机械伺服雷达，相控阵雷达具有形成波束指向、波束形状快速变化［1］、无惯性空域扫描等优点。圆柱阵作为典型的共形阵，与方位机械伺服、俯仰相扫的平面阵［2］相比具有探测性能覆盖均匀［3］，二维相扫，波束调度灵活等优势，因此在雷达、声纳等领域受到广泛关注。但圆柱阵相比平面阵，存在方向图副瓣水平较高的问题。对于相控阵雷达，让阵列天线的方向图保持低副瓣水平能够在一定程度上实现杂波抑制［4］，因此需要对圆柱阵的副瓣进行控制。对于圆柱阵列，目前较为常见的处理方法是将其二维方向图函数近似为一维圆环/圆弧阵的方向图函数和一维线阵的方向图函数的乘积，由此实现圆柱阵列波束形成权值在方位和俯仰维的解耦［5］，从而将问题的难点转变为对圆环/圆弧阵实现低副瓣方向图综合。

在平面阵中，常用幅度加权法得到低副瓣波束，如Taylor 综合法、Dolph-Chebyshev 综合法等，但这些方法无法直接应用在共形阵上。因此，国内外学者目前大多采用数值综合类方法进行共形阵的低副瓣方向图综合。自Franceschetti于1990年提出著名的交替投影法以来，不少学者利用该算法进行共形阵的低副瓣波束形成。2002 年，Steyskal 利用交替投影法对布阵在飞机机翼上的116元共形阵进行低副瓣方向图综合［6］。2008 年，陈云等人利用改进的交替投影法对旋转抛物面（GPOR）上的2 个共形相控阵天线进行方向图综合［7］。2012 年，赵菲对交替投影法进行改进，使算法陷入局部最优的可能性大幅降低［8］。但交替投影法无法解决实际应用中更加关心的问题：在固定的主瓣宽度下实现方向图的最低等副瓣电平。这实际上与线阵的Dolph-Chebyshev综合法一样，是一个最优解问题。

随着智能算法的不断发展，不少学者利用遗传算法、粒子群算法和模拟退火等智能算法进行共形阵的低副瓣方向图综合［9-11］。这类智能算法虽然具备鲁棒性好、陷入局部收敛的可能性小等优点，但相比于其他类型的算法，该类算法收敛所需的迭代次数较多。且这类算法在实施时，大多需要先预设一个给定主瓣宽度和副瓣电平的期望方向图，然后对其不断逼近，而对于某个确定的阵列来说，这个问题可能是无解的（即在预设的主瓣宽度下，方向图的副瓣不可能达到期望的水平）。

随着凸优化理论的发展，不少学者将共形阵的方向图综合问题转化为利用凸优化方法来进行半正定规划（Semi-Definite Programming，SDP）和二次锥规划（Second-Order Cone Programming）［12-13］。这类方法虽然能够解决方向图综合中的最优解问题，但却十分依赖第三方凸优化软件包，且初始权值的选取对算法的收敛有极大的影响。更重要的是，当阵列的形状不规则且对方向图的约束条件较多时，凸优化算法有可能陷入局部最优而非全局最优。

还有一种基于自适应阵原理的波束形成方法：虚拟干扰法。1990 年，Olen 和Compton 第一次系统地将自适应波束形成的原理运用在任意阵列的方向图综合上。Olen 等人通过在已知波束期望指向的前提下，对方向图的副瓣区域设置大量虚拟干扰来实现阵列的低副瓣方向图综合，但该方法存在迭代次数较多、迭代系数、虚拟干扰个数选取模糊和算法收敛性存疑等问题。后续，学者刁跃龙针对当前算法存在的问题提出了改进算法，新算法不仅迭代次数较少、迭代系数易于选取，而且能解决实际应用中更关心的固定主瓣宽度下的最低等副瓣电平问题，这使得算法的收敛性不再存疑［14］。2009 年，刘聪锋等人通过对迭代公式进行改进，使算法的收敛速度进一步加快［15］。2018年，毕杨等人利用该算法解决了恒定相应宽带波束形成问题［16］。但该算法目前仍存在干扰个数取值模糊的问题。在算法运用上，学者蒋立志将虚拟干扰法用于圆柱阵的低副瓣波束形成，并对分步综合法与直接综合法进行了对比［5］，但其研究未考虑工程应用条件下的阵元有向性和结构遮挡效应等因素。

本文研究了基于分布综合法的圆柱阵低副瓣波束形成方法，在方位维一维圆弧阵进行低副瓣波束形成时，提出了一种基于虚拟干扰法的改进算法，新算法能通过干扰采样比来确定干扰个数，从而避免了算法实施过程中对干扰个数的盲目选取，这对实际工程应用有一定的指导意义。本文还对圆柱阵波束指向偏离法向后分步综合法误差进行了评估，得出了在圆柱阵的波束指向小范围偏离法线（±20°内）时算法性能良好的结论。最后，实测数据验证了算法的有效性。

2 圆柱阵模型及其方向图函数

圆柱阵模型及其阵元排布如图1所示。阵列在Z轴方向均匀排列着N层圆环，每层圆环上均匀排列着M个阵元。其中，圆环半径为R，相邻圆环的间距为h。

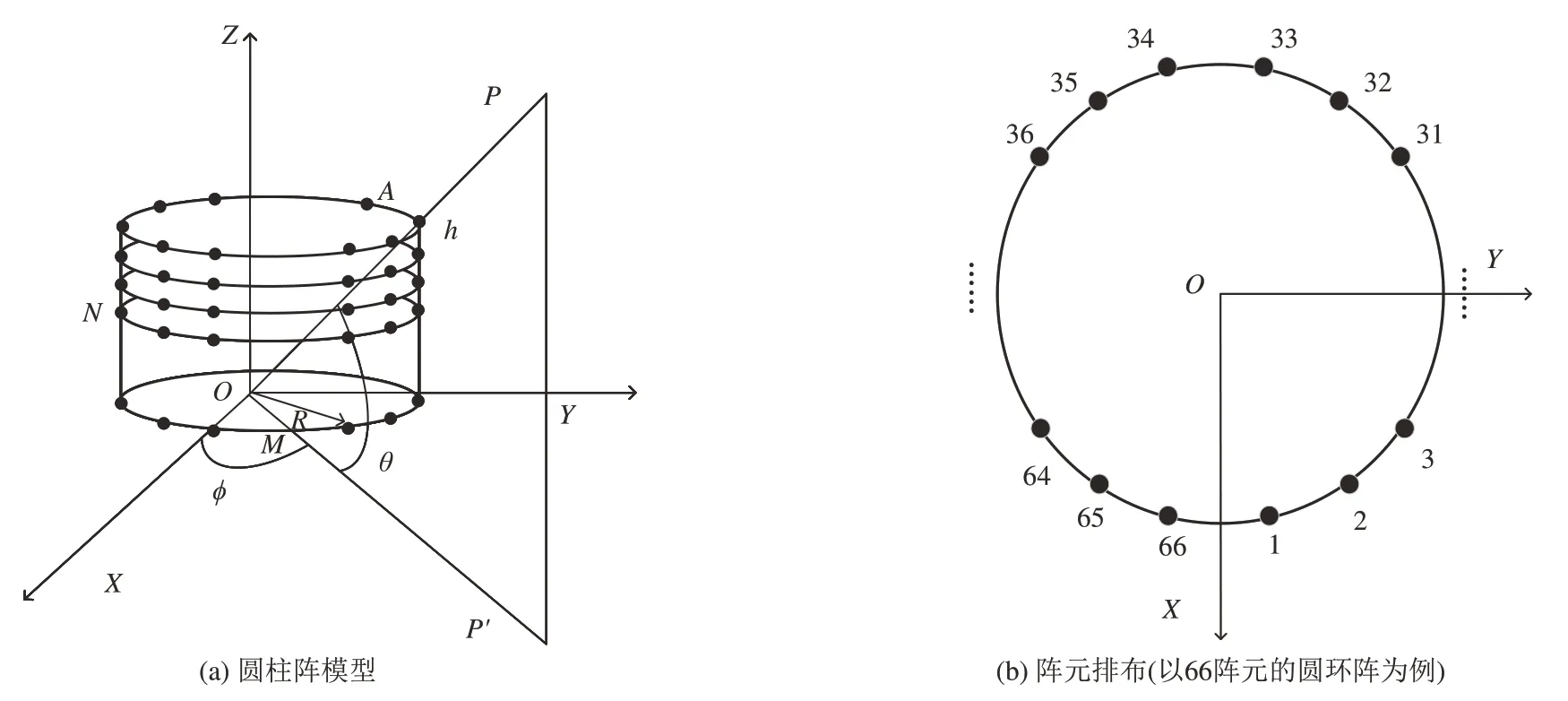
图1 圆柱阵模型及其阵元排布方式Fig.1 The model of cylindrical array and its array element arrangement

设远场来波方向为(ϕ，θ)，方位角ϕ∈[-180°，180°)，俯仰角θ∈[0°，90°]。将阵列的第n层圆环的第m个阵元（n=1，2，…，N；m=1，2，…，M）记为A，以坐标原点O为参考相位，阵元A的方位角记为ϕnm，俯仰角记为θn。在阵元A接收到来自远场(ϕ，θ)方向的信号后，A和O之间的相对相位（即空间相位差）为

因此

要使波束指向对准来波方向，就要对每个阵元施加一个相位，使其抵消空间相位差。因此，圆柱阵的方向图函数可表示为

其中，anm表示第n层圆环的第m号阵元的相位。当波束指向（ϕ0，θ0）时

根据公式（7）可知，圆柱阵的本质是以圆环阵为阵元的均匀线阵。考虑阵元的有向性，取单元方向图函数［17］为

其中，ϕm为第m个阵元的方位角。基于有向阵元的圆柱阵的方向图函数为

其中

实际情况中，由于结构遮挡效应，圆柱阵在形成波束时只利用某个扇区（如120°）的阵元。若这个扇区在圆环上对应K个阵元，则圆柱阵的方向图函数可表示为

其中

根据公式（11），基于有向阵元和遮挡效应的圆柱阵的方向图可以分两步合成：第一步先进行二维弧阵波束合成，第二步以圆弧阵为阵元进行线阵波束合成，即圆柱阵可以通过两级子阵分步进行波束形成［18］。

对于公式（9），当θ0较小时，cosθ0≈1，有以下近似

即圆柱阵权值wcylindrical可表示为圆弧阵权值warc和线阵权值wline相乘［5］

3 圆柱阵低副瓣波束形成算法

3.1 虚拟干扰法简介

虚拟干扰法利用最大信噪比准则来进行波束形成，通过在方向图的副瓣区设置大量干扰来实现方向图整体副瓣水平的降低。Olen和Compton对该算法进行了详细的研究，并提出了基于自适应阵列原理的任意阵列方向图综合算法，其核心思想为：

人为地在方向图副瓣区域均匀设置大量的干扰（干扰数量需大于阵元数），因为阵列的波束是自适应形成的，所以方向图会在副瓣区进行自我调整并不断完善，如果某个方向对应的方向图副瓣较高，则增大该处的干扰强度，反之则减小该处的干扰强度。算法在不断迭代的同时对干扰强度进行调整，从而不断地对方向图的副瓣区域进行调整，最终实现低副瓣波束形成［15］。由于该方法可用于任意阵列，因此受到广泛关注。

Olen和Compton的算法先确定期望波束指向的方向矢量v(θ0)，接着设置期望得到的副瓣电压d(θ)。如果在θ处方向图的副瓣比主瓣低VdB(θ)（分贝值），且方向图的峰值电压为Vpeak，则在θ处方向图的期望副瓣水平为

假设噪声均为白噪声，SNR（信噪比）和INR（干噪比）的定义为

代表信号和干扰的功率。

若在方向图副瓣区同时设置Ni个虚拟干扰，令初始的干噪比INR=1。根据虚拟干扰法，在每个干扰的位置都要将对前方向图的电压值与期望方向图的电压值做差处理，若差值大于0，则增加该处干扰功率，反之，减小该处干扰功率［16］。这里要注意的是，在调整干扰功率后，利用MSINR（最大信干噪比）准则得到的权值也在变化。因此，波束形成器的输出d(θ)也在变化，第k次迭代时

其中，Vpeak(k)表示第k次迭代时方向图的峰值电压。该算法的干扰迭代公式为［14］

其中，i=1，2，…，Ni。(θLeft(k)，θRight(k))表示方向图主瓣区，该区域内干扰功率被置零，inri(k)表示第k次迭代时θi方向的干扰功率，Q为迭代系数，Q>0。∆(θi，k)表示第k次迭代后在θi方向上当前方向图的电压值与期望方向图的电压值之差，用公式表示为

这里应格外注意的是，由于干扰的强度不断变化，波束形成器的权值也变化，因此方向图的主瓣区也在随之改变。因此，每次迭代后要重新确定主瓣区域。

尽管Olen 和Compton 的算法能够实现任意阵列低副瓣方向图综合，但该方法仍然存在Q和Ni取值模糊的问题，且该算法解决的是固定主瓣宽度和PSLR 下低副瓣方向图的综合问题，在这种条件下，问题不一定有解［14］。而且，实际中往往更关心固定主瓣宽度下方向图能达到的最低PSLR。

针对Q取值模糊的问题，学者刁跃龙对算法进行了改进［14］。算法改进后新的迭代公式为

公式（20）考虑了干扰功率间的相对大小，且对每次迭代后的电压差Δ(θi，k)进行归一化处理，因此与原算法相比，学者刁跃龙的算法收敛速度更快，Q值更容易选取。

为了解决实际问题中固定主瓣宽度下实现最低PSLR的问题，学者刁跃龙重新定义参考电压［14］

这样，随着算法不断迭代，所有副瓣都会向d靠近，而由于d本身也在不断变化，随着迭代次数增加，结果不断收敛，所有的副瓣峰值都与d趋于一致，因此该算法一定有解。固定主瓣宽度下的最低PSLR的低副瓣方向图综合算法的步骤如下：

（1）在整个空域内均匀设置大量干扰并对干扰功率赋初值，根据需求设置方向图主瓣区域并将干扰强度置零；

（2）利用MSINR 准则计算权值，并根据权值计算初始方向图，求出参考电压d；

（3）用公式（20）更新干扰功率，并在最大信干噪比准则下求得波束形成器的权值；

（4）重复步骤（2）和（3），直至结果收敛。

值得注意的是，由于改进算法的主瓣宽度是固定的，因此不需要每次迭代后重新计算主瓣范围，这在一定程度上也减少了计算量。

3.2 算法改进

目前，虚拟干扰法经过不断完善，呈现出Q易于取值（一般取0～1内的值即可），迭代次数少（通常迭代数十次即可收敛）等优点。但对于干扰个数的选取通常为：干扰个数Ni是阵元数的2～3倍以上［14］。然而，在算法实施过程中，实验者需要多次尝试才能得到合适的Ni值。因此，干扰个数Ni的取值是较为模糊的，且当干扰个数满足阵元数的2～3倍以上时，在不同的方向图采样间隔下，算法收敛情况也不尽相同。下面以圆弧阵的低副瓣方向图综合为例，说明虚拟干扰法中虚拟干扰个数对算法收敛的影响。

仿真1：采用文献［16］所述的算法对表1 所述圆弧形进行仿真。

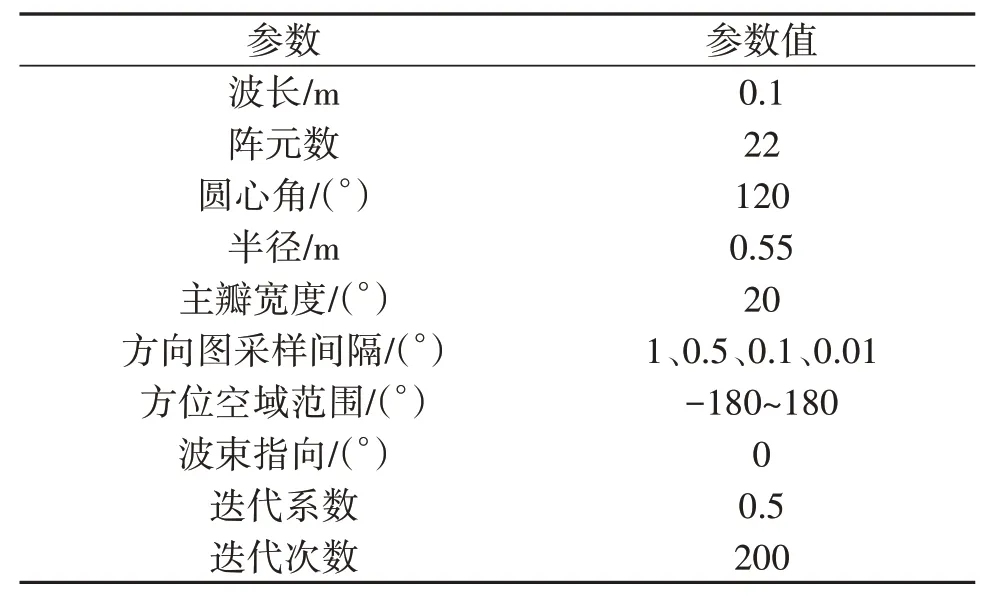
表1 圆弧阵仿真参数Tab.1 Simulation parameters of arc array

根据大多数文献对虚拟干扰个数的描述，干扰个数取阵元个数的2～3 倍以上。因此，本仿真取干扰个数分别为70、80、100、120、150 和300（均为本仿真中圆弧阵阵元个数的2～3倍以上），然后进行圆弧阵的低副瓣方向图综合。仿真时，单元方向图取公式（8）。仿真结果如图2 所示。为保证算法充分收敛，迭代次数选取200次。

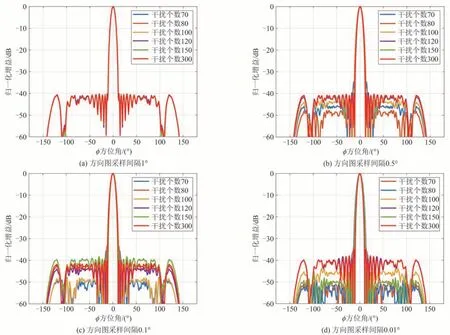
图2 不同虚拟干扰数目下方向图收敛情况Fig.2 The convergence of pattern with different numbers of virtual interference

根据图2所示仿真结果，当方向图采样间隔为1°时，方向图均能达到收敛；当方向图采样间隔为0.5°，当干扰个数为120个以上时，算法基本收敛；当方向图采样间隔为0.1°时，即使干扰个数为150个，算法仍未收敛；而当方向图采样间隔为0.01°时，干扰个数为300个时算法仍不能收敛。由此可知，并非只要干扰个数满足大于阵元数的2～3倍，就一定能保证算法收敛，算法收敛情况不仅与虚拟干扰个数密切相关，还与方向图采样间隔有关，方向图采样间隔越密集，使方向图收敛所需要的虚拟干扰个数就越多。如果只遵循原算法的干扰个数选取规则，就需要采用累试法来不断试验，这无疑增加了算法实施的困难。为研究干扰个数与方向图采样间隔的关系，定义干扰采样比为

然后不同干扰采样比下对算法的收敛情况进行分析。其中，Ni和Ns分别表示副瓣区干扰个数和方向图采样点数。后文中，ISLR、FNVW和HRPW分别表示积分旁瓣比、第一零点波束宽度和半功率波束宽度。

仿真2：采用文献［14］所述的改进算法对表2所示圆弧形进行仿真。

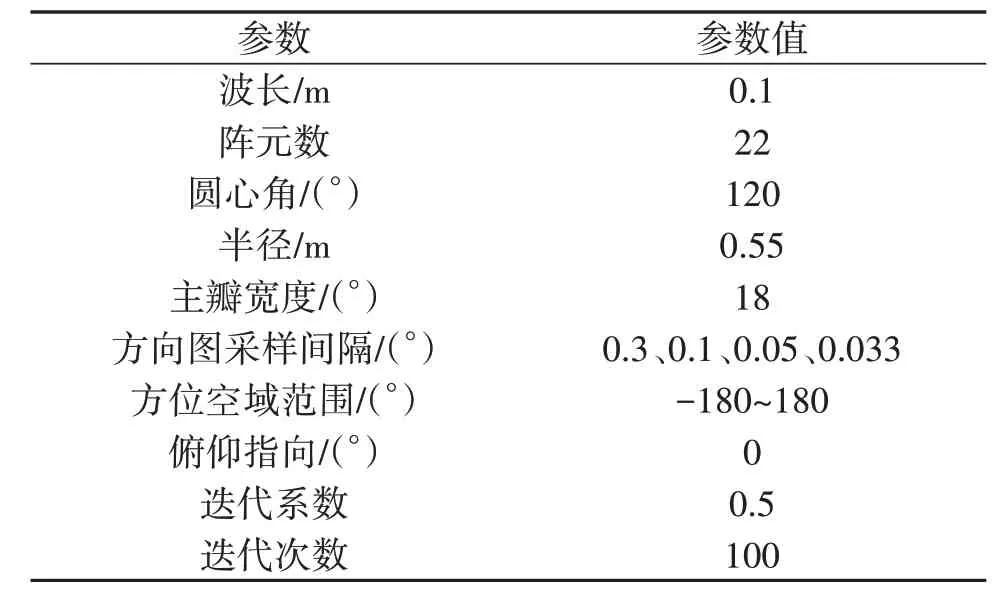
表2 圆弧阵仿真参数Tab.2 Simulation parameters of arc array

仿真时，单元方向图仍然取公式（8）。仿真结果如图3所示。

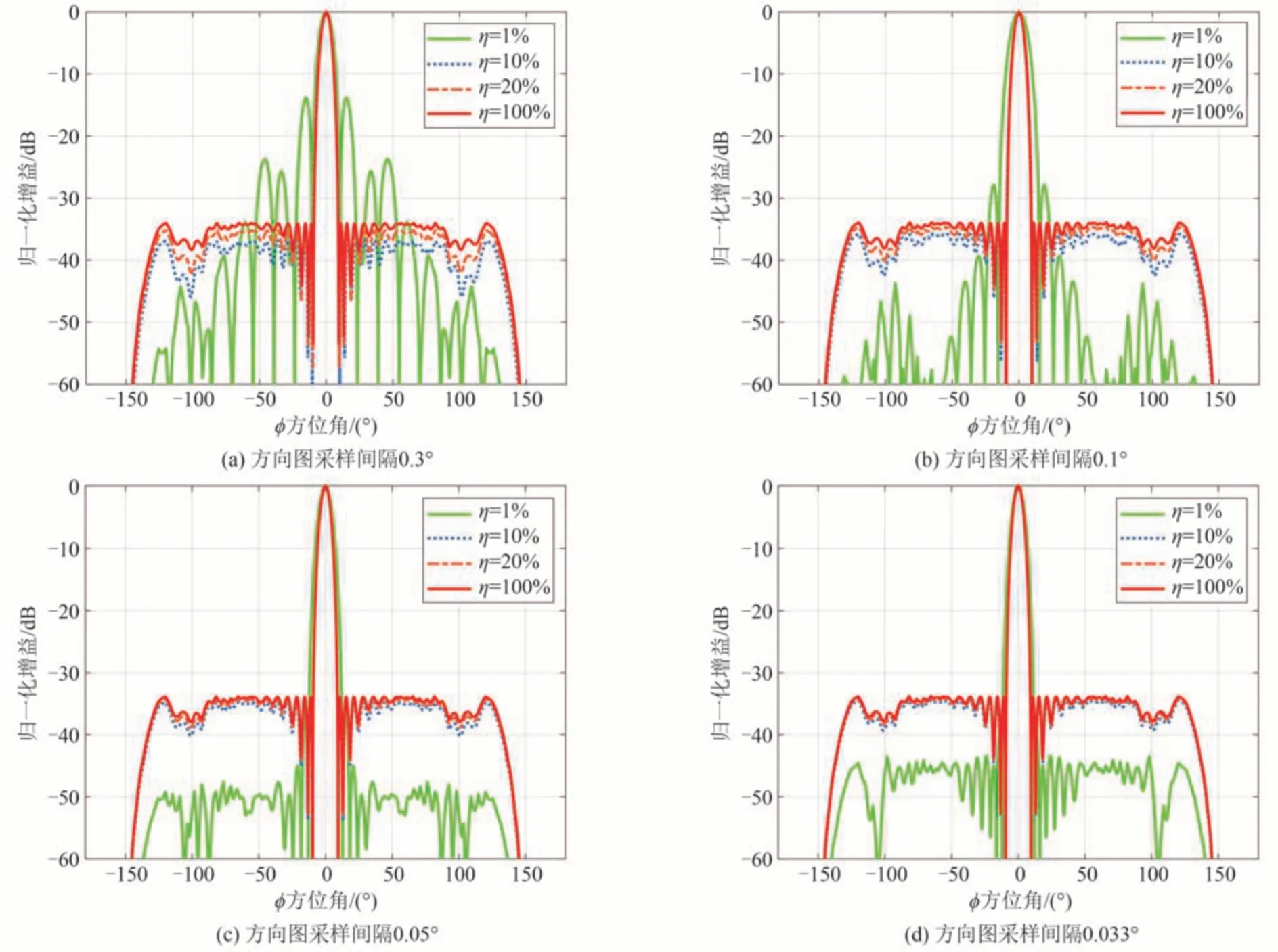
图3 不同干扰采样比下的方向图Fig.3 Patterns in different interference sampling ratio

接着分析η和方向图主要参数（如PSLR、ISLR、FNVW和HRPW）的关系，结果如图4所示。

图4 不同干扰采样比下的方向图主要参数Fig.4 Main parameters of pattern in different interference sampling ratio

根据图4，有以下结论：（1）在不同方向图采样间隔下，当η<20%时，PSLR、ISLR、FNVW 和HRPW 均有较大波动，此时算法并未收敛。（2）在不同方向图采样间隔下，当η≥20%时，PSLR、ISLR、FNVW和HRPW随着η的增大均逐渐趋于稳定，此时的FNVW随着η的增大而不断接近算法在开始时预设的将干扰功率置零的主瓣宽度18°。

因此，在算法的工程应用中，可以用干扰采样比来确定虚拟干扰的选取个数。当虚拟干扰个数满足η≥20%时，算法能实现基本收敛（但首先需满足文献［14-16］的基本条件，即干扰个数必须大于阵元个数的2～3 倍），η越大，收敛效果越好，但所需的计算量也越大。

3.3 圆柱阵低副瓣波束形成方法

采用公式（13）和（14）对圆柱阵进行二维波束图分布综合仿真实验。

仿真3：利用图1 所示结构的圆柱阵进行分步综合法仿真，单元方向图见公式（8）。在阵列方向图不产生栅瓣［19］的前提下对圆柱阵的阵元进行合理排布，考虑阵结构遮挡，每次用1/3 阵面合成一个波束，对于圆弧阵，采用本文所述的改进算法，对于线阵则加-30 dB的Taylor窗，具体仿真参数见表3。

表3 圆柱阵仿真参数Tab.3 Simulation parameters of cylindrical array

首先分析波束指向为法向时的情况。圆柱阵波束形成结果如图5和图6所示。

图5 圆柱阵初始波束和低副瓣波束Fig.5 Initial beam and low sidelobe beam of cylindrical array

图6 低副瓣方向图和初始方向图比较Fig.6 Difference between low sidelobe pattern and initial pattern

根据图6可知，仿真结果符合预期，副瓣得到了有效压制。然后对波束指向逐渐偏离法向后的产生的误差进行分析。波束指向取(0°，10°)，(0°，20°)，(0°，30°)和(0°，40°)，将圆柱阵方位剖面与其对应圆弧阵的方向图进行对比。结果如图7所示。

图7 圆柱阵和圆弧阵方位维方向图对比（不同俯仰指向）Fig.7 Difference between azimuth pattern of cylindrical array and arc array（different elevation direction）

接着，将波束指向取（10°，0°），（20°，0°），（30°，0°）和（40°，0°），将圆柱阵方位维剖面与对应的圆弧阵的方向图进行对比，结果如图8所示。

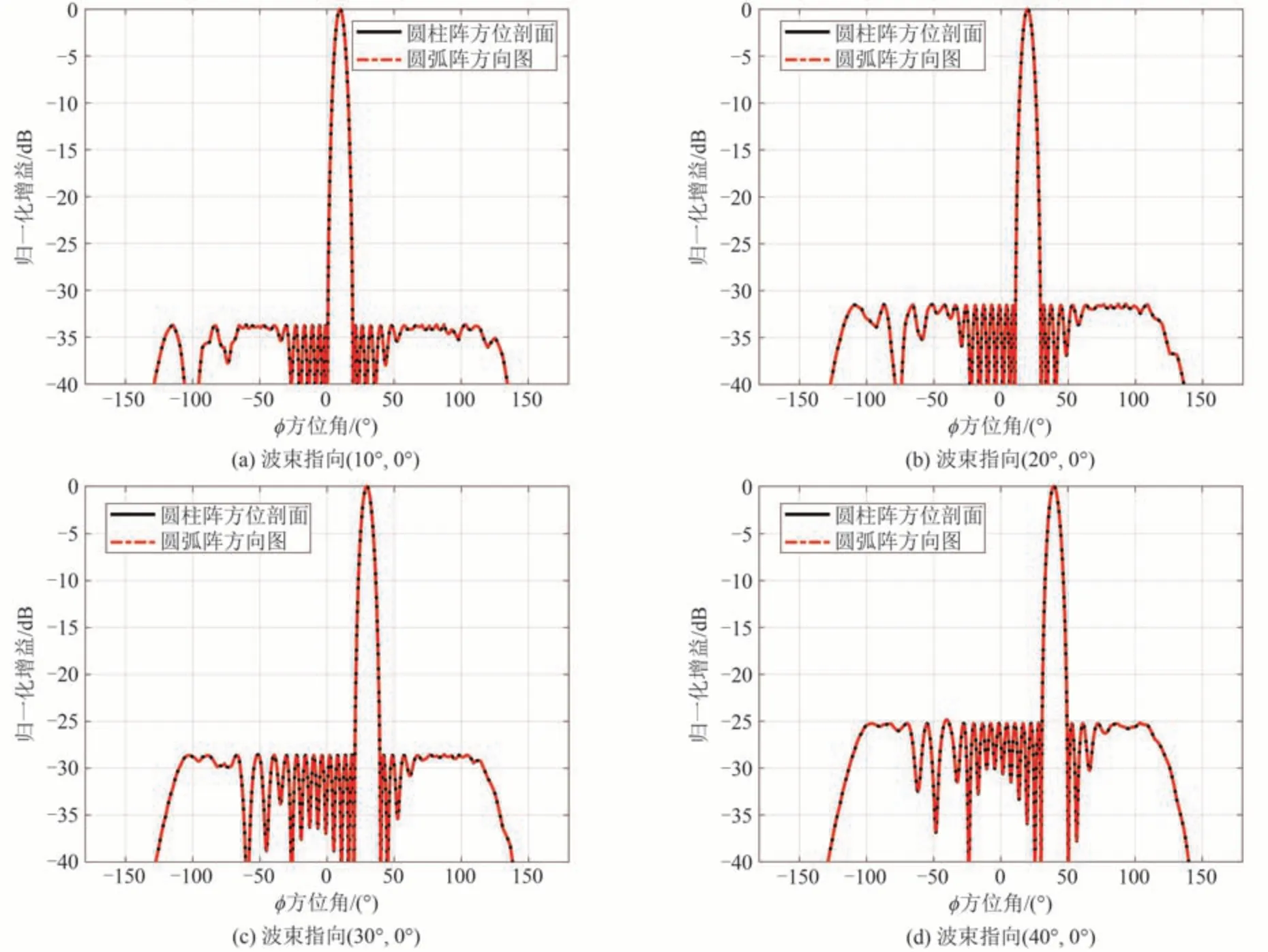
图8 圆柱阵和圆弧阵方位维方向图对比（不同方位指向）Fig.8 Difference between azimuth pattern of cylindrical array and arc array（different azimuth direction）

最后，将波束指向取(10°，10°)，(20°，20°)，(30°，30°)和(40°，40°)，分析方位与俯仰指向同时改变的情况，仿真结果如图9和图10所示。

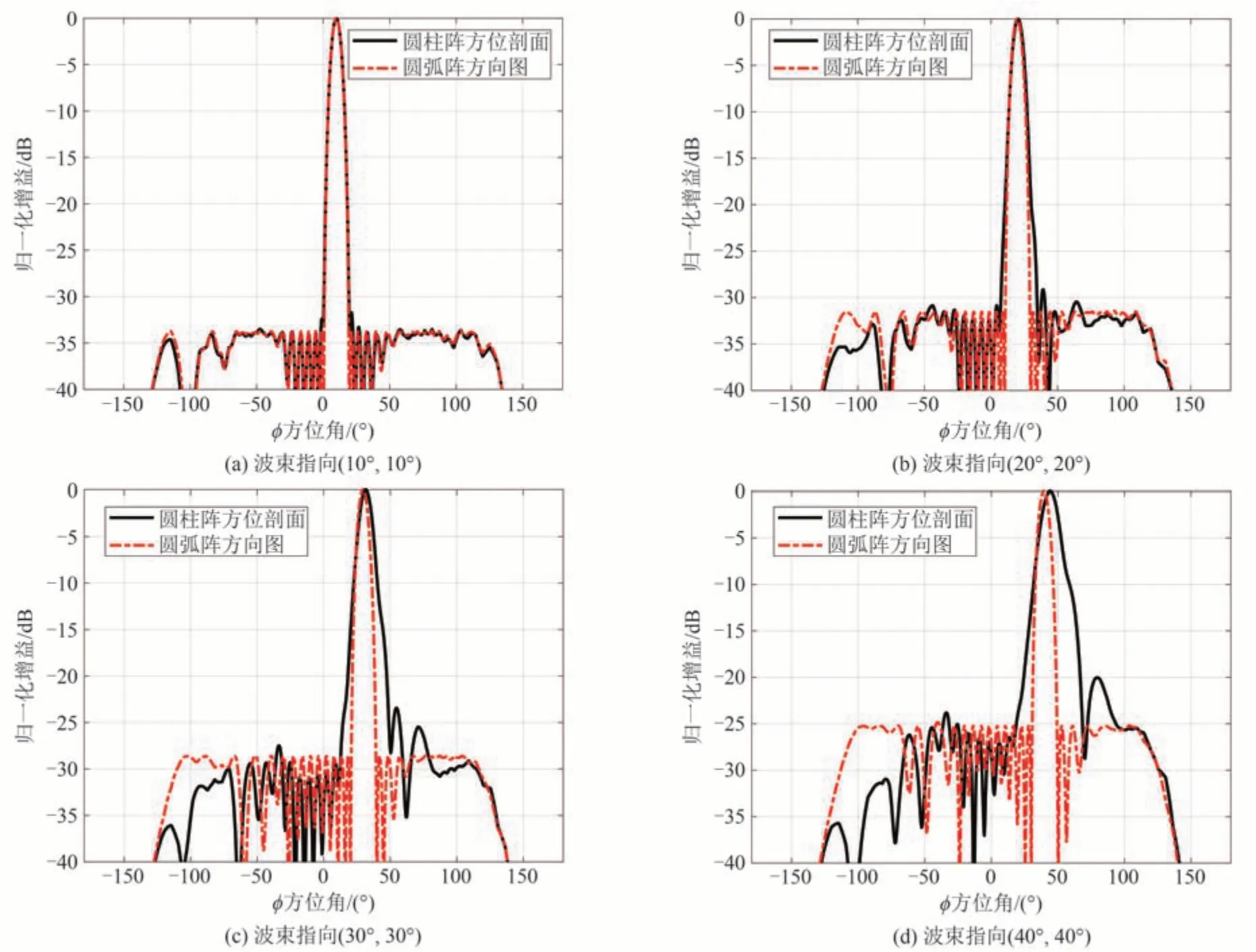
图9 圆柱阵和圆弧阵方位维方向图对比（方位、俯仰指向同时改变）Fig.9 Difference between azimuth pattern of cylindrical array and arc array（azimuth and elevation direction change simultaneously）

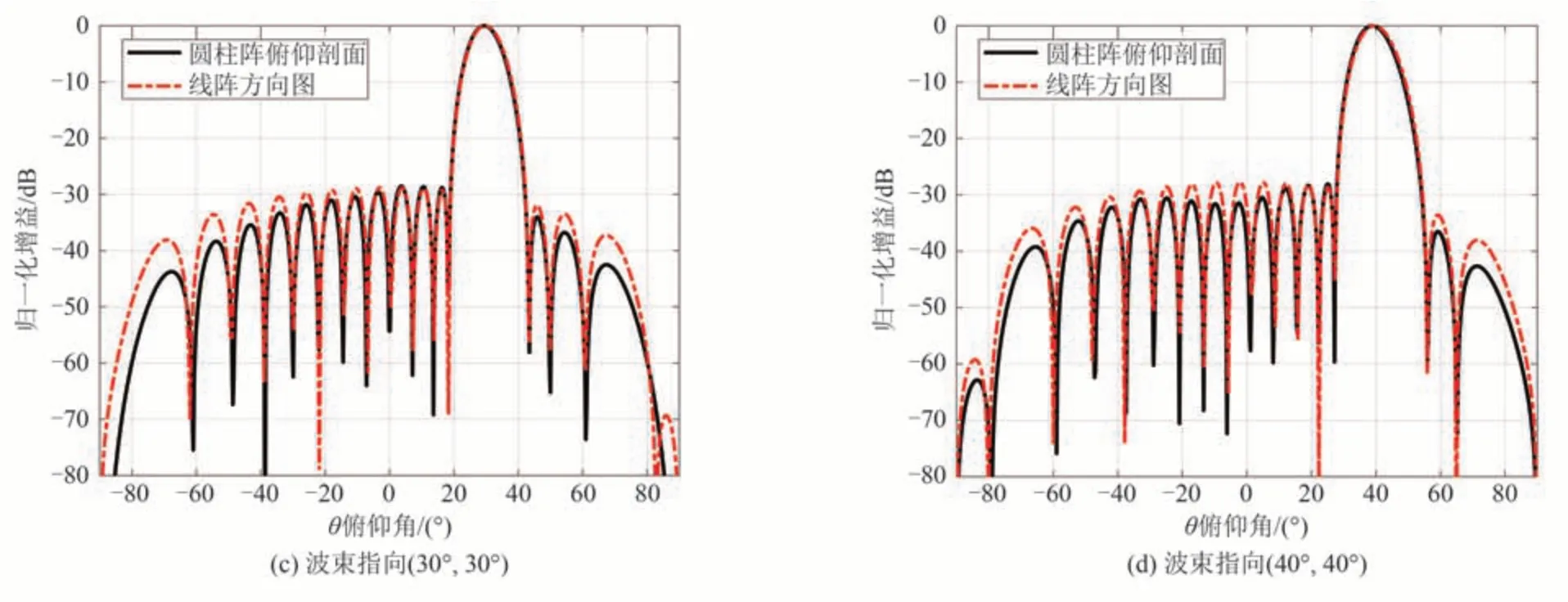
图10 圆柱阵和圆弧阵方位维方向图对比（方位、俯仰指向同时改变）Fig.10 Difference between elevation pattern of cylindrical array and arc array（azimuth and elevation direction change simultaneously）

通过对图7～图10分析，有以下结论：（1）根据图7可知，在方位指向法向，俯仰指向由10°到40°逐渐增大时，采用分步综合法得到二维波束图方位剖面图与对应的圆弧阵方向图相比质量逐渐变差（尤其是θ>20°后），PSLR 分别增大2.1 dB、4.0 dB、6.2 dB 和12.3 dB，HRPW 分别展宽1.5%、5.8%、28.9%和92.5%，且方位维波束指向不变。（2）根据图8可知，在俯仰指向法向，方位指向逐渐增大时，采用分步综合法得到二维波束图方位剖面与其对应的圆弧阵相比能够完全保持一致，根据公式（11），这是因为圆柱阵的方位维方向图仅由圆弧阵所决定。但当波束偏角距法线较大时，方向图的副瓣有较大抬升，因此不适合在方位维进行大范围扫描。（3）根据图9和图10可知，同时增大俯仰和方位指向，采用分步综合法得到二维波束图在俯仰维能保持较好的质量，在方位维则迅速恶化（尤其是θ>20°后），方位维方向图的PSLR分别增大2.1 dB、2.5 dB、5.2 dB 和10.1 dB，HRPW 分别展宽2.1%、13.9%、41.7%和62.5%，且在波束指向偏离法向20°以上时，波束指向产生了较大的偏移。

3.4 阵列误差对方向图的影响

考虑实际工程应用中，阵列存在不可避免的幅相误差。现对幅相误差对圆柱阵低副瓣波束的影响进行仿真分析。采用表3所述的圆柱阵进行方位维低副瓣方向图仿真，将主瓣宽度限制为16°，方向图采样间隔取0.5°，其他参数不变，仿真时同时引入±3°、±5°、±7°、±10°、±15°和±20°的相位误差和±0.3 dB、±0.5 dB、±0.7 dB、±1 dB、±1.5 dB 和±2 dB的幅度误差，仿真结果如图11所示。

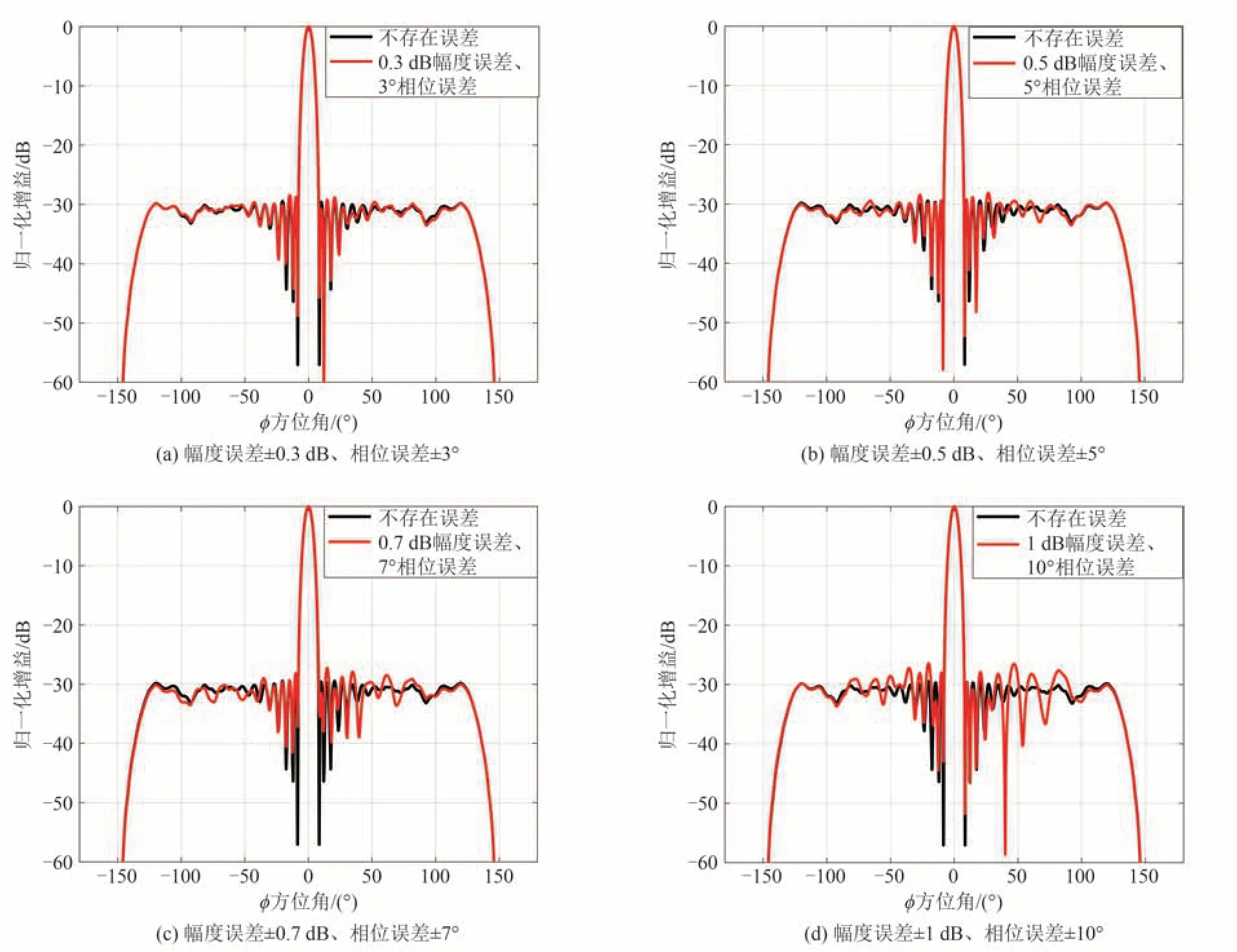
图11 幅相误差对方向图的影响Fig.11 The influence of amplitude and phase errors on pattern

从图11 所示结果可知，随着幅相误差不断增大，方向图的副瓣电平逐渐抬高，且逐渐失去等副瓣特性。当幅相误差达到±1 dB，±10°时，相比于无幅相误差的情况，方向图副瓣抬高了3.5 dB。因此在实际系统中，要尽量减小阵面的幅相误差。

3.5 实测数据验证

采用某S波段圆柱相控阵雷达（实物照片如图12所示）在微波暗室进行远场方向图测量实验，雷达经过标校后，存在约±1 dB，±10°的幅相误差。将雷达架设在高精度转台上，调整远区测试天线的高度和指向，使其对准圆柱阵中心，然后旋转转台，以此测试圆柱阵方位维的方向图。对于俯仰维的方向图，则在微波暗室中利用远场高精度扫描架进行俯仰维波束方向图测量。

图12 某S波段圆柱形相控阵雷达Fig.12 A cylindrical phased array radar with S-band

采用本文所述方法将圆柱阵的主瓣宽度控制在16°（如图11（d）所示，在该主瓣宽度下，圆柱阵方位维方向图的理论副瓣电平均被控制在-26.5 dB以下），并对俯仰维加-30 dB的Taylor窗后进行暗室方向图实测，测试结果如图13所示。

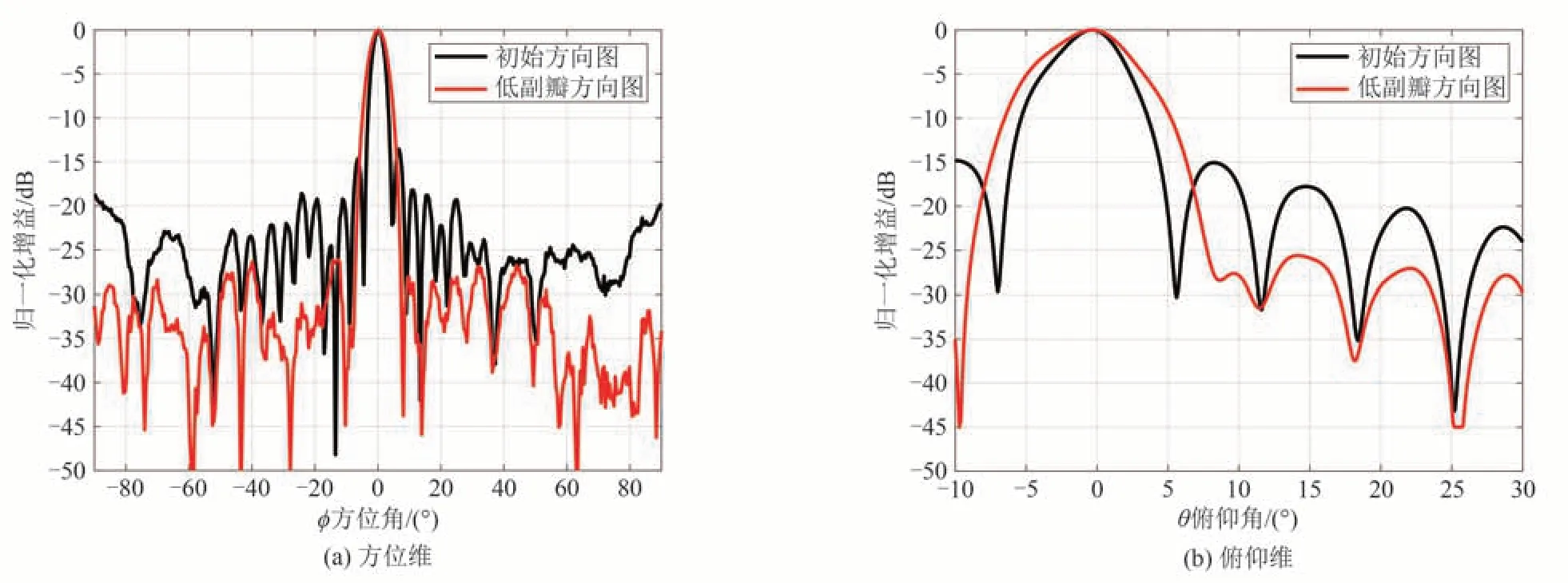
图13 初始方向图与低副瓣方向图对比（微波暗室内）Fig.13 Comparison of initial pattern and low sidelobe pattern（in microwave anechoic chamber）

根据图13所示的实测结果可知，圆柱阵方位方向图最高副瓣为-26.0 dB，俯仰维方向图最高副瓣为-25.8 dB，方位俯仰副瓣均被抑制在-25 dB 以下，以此验证了本文所述算法的有效性。

4 结论

本文针对圆柱阵副瓣较高的问题，研究了分步综合方法，将圆柱阵的二维波束分解为方位维一维圆环/圆弧阵波束和俯仰维一维线阵波束，将问题的核心转变为对方位维一维圆环/圆弧阵进行低副瓣波束形成。针对方位维的圆弧阵，本文提出了一种虚拟干扰法改进算法，通过采用干扰采样比来确定干扰个数，解决了算法实施过程中干扰个数选取模糊的问题。计算机仿真结果表明，在圆柱阵波束方位和俯仰指向左右偏离中心法线20°范围内，采用分布综合法可将圆柱阵方位和俯仰维方向图的副瓣抑制到-30 dB 以下。本文还对存在幅相误差时方向图副瓣的恶化程度进行了定量分析，当幅相误差达到±1 dB，±10°时，圆柱阵方位维方向图副瓣将抬高3.5 dB。最后，项目组利用圆柱阵样机和微波暗室进行方向图测试实验，实测结果表明，圆柱阵方位与俯仰方向图的副瓣均被抑制在-25 dB 以下，这与存在幅相误差时的理论值较为接近。