典型风电场地形大气稳定度对风机出力的影响

王彬滨 ，余江 ，张荣 ，孙朋杰

（1.四川电力设计咨询有限责任公司,四川 成都 610041；2.西昌学院,四川 西昌 615000；3.中国气象局气象干部培训学院湖北分院,湖北 武汉 430074；4.湖北省气象服务中心,湖北 武汉 430074）

0 引言

我国提出力争在2030 年前实现碳达峰，努力争取2060 年前实现碳中和的目标。“3060 双碳”目标的提出必将加快推动风电、太阳能等新能源的跨越式发展。“十四五”期间，我国新能源将进入快速发展期，据权威机构预测，按照目前进度，到2030 年风电光伏总装机容量超过1.2 TW 的可能非常大。风能作为一种绿色可再生能源，对于人类社会可持续发展具有重要的意义[1-3]。准确的风能资源和发电量评估可以减小风电场投资建设决策风险，提升风能资源、土地资源等利用效率，是风电场开发建设至关重要的一环[4-6]。

在国内外风能资源相关领域的研究和实际工程应用中，以气象研究与预报模式（Weather Research and Forecasting model，WRF）、CFD 为核心的技术方法已经广泛使用。惠小英等[1]应用WRF 模式对酒泉地区风场进行了数值模拟试验，结果表明模拟的风能密度与实际观测结果较为一致；张鸿雁等[7]利用WRF 模式对湖北省风能资源进行模拟，结果表明模拟结果能反映出风能资源分布的趋势；郁永静等[8]应用WRF 气象模式进行高海拔无测风复杂地形区域风能资源分布模拟,并将模拟结果、美国国家航空航天局发布的全球再分析气象数据集产品（以下称MERRA）数据分别与实测数据进行对比分析。研究表明，WRF 模拟具有较高的模拟精度,且效果明显优于MERRA 数据；谢今范等[9]利用中尺度模式WRF进行东北地区风能资源空间模拟,研究观测站点稀少地区的风能资源分布特征，研究结果表明：中尺度模式WRF 能够较好地模拟东北区域风速分布的气候特征；魏慧荣等[10]在早些年前为把CFD 技术应用于风场中实际地形的风流动模拟，选择典型地形进行数值模拟，对比了不同网格和不同湍流模型对风流场模拟分布结果的影响；李军等[11]将中尺度天气模式输出当作边界条件输入给CFD，初步显示中尺度天气模式结合CFD 的方法可更好地模拟复杂地形的大气边界层运动；方艳莹等[12]运用中尺度数值模式WRF 与法国CFD 软件相结合的方法，进行了广东省海陵岛地区的风能资源数值模拟试验，结果表明：中尺度模式与CFD 软件结合的数值模拟方法对区域风能资源分布趋势的模拟比单纯应用CFD 软件更准确。

风是由太阳辐射热引起的空气流动现象，大尺度风的两个主要驱动因子是赤道和极地之间的加热差异和地球自转，而影响大气边界层风流特征主要包括地形、粗糙度以及大气稳定度。大气稳定度的定义主要有4 类，都是表征大气稳定的程度。传统的风能资源研究和工程应用中，大气稳定度几乎都被假定为中性，随着国内外风电场开发建设的持续推进和后评估研究工作的完善，大气稳定度对风能资源影响的显著性开始得到风能资源相关领域的学者和工程人员的重视，特别是低风速选址区域，热效应对风流特征的影响变得显著，其显著性可能超过地形和粗糙度。张双益等[13]通过对大型海上风电场的尾流数值计算结果对比，探讨了海上大气稳定度对风电场风能资源的影响；TEXIER 等[14]考虑了在进行CFD 技术风能资源评估时引入大气稳定度的影响。目前对典型风场地形大气稳定度对风能资源和风电场出力影响机理的比较研究仍较少，可用于研究大气稳定度热效应的实际观测数据也不易收集。本文选取了平坦和复杂山地两种典型风电场地形，使用上述地形两座测风塔不同高度观测数据，包括多层高度的风速、气温、气压等资料，通过大气稳定度的比较计算，定量地探讨大气稳定度对风能资源和风机出力的影响，以期给风能资源研究和风电场工程应用提供一定的技术支撑。

1 资料简介

本文使用两座观测塔（图1 和图2）采集的观测资料。观测塔1 高100 m，安装点海拔高度12 m，位于中国东部长江中下游地区，临靠长江，所在区域地势由西北向东南缓斜且总体平坦，海拔范围为10～100 m，地貌主要呈现为小丘陵和平原阶梯状分布，气候态属亚热带季风气候区。观测塔2 高80 m，安装点海拔高度2.55 km，位于中国中部地区秦巴山区腹地，所在区域地势由南、西向东北倾斜，高差大，坡度陡，是典型的中部复杂山区地貌，海拔范围为1.5～2.5 km，为副亚热带季风大陆性气候。

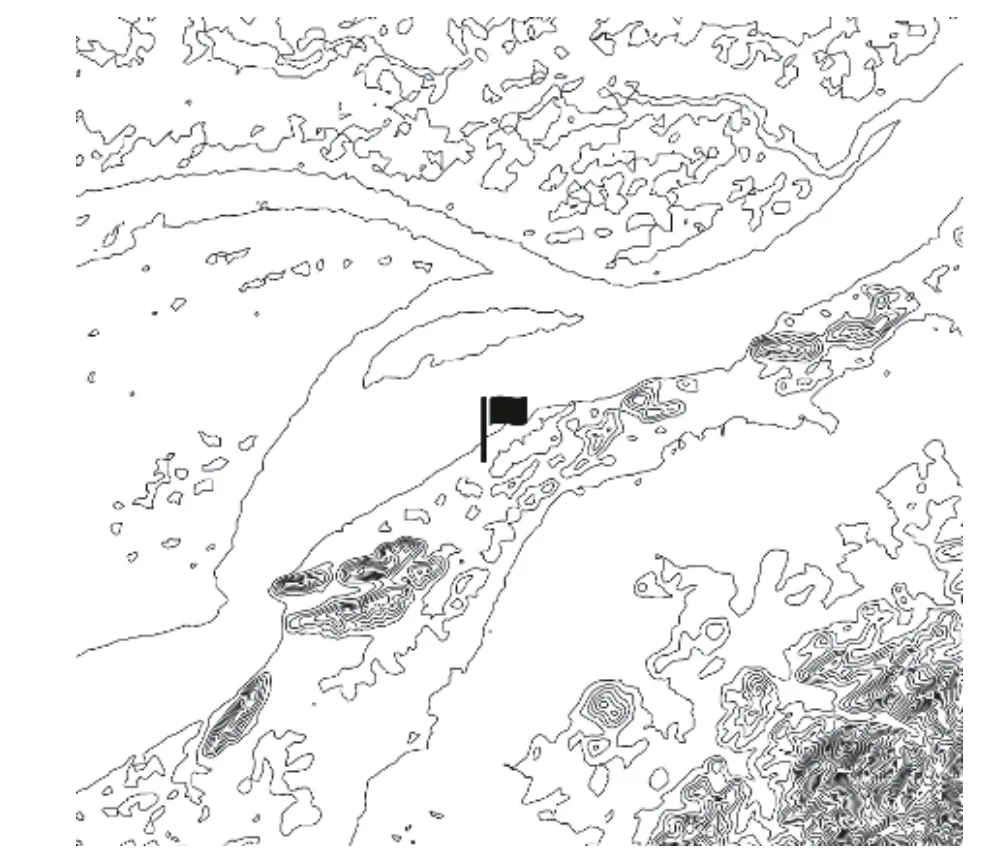
图1 观测塔1 海拔地形示意图（区域海拔范围10～100 m）Fig.1 Elevation topography of observation tower 1(regional elevation range: 10～ 100 m)

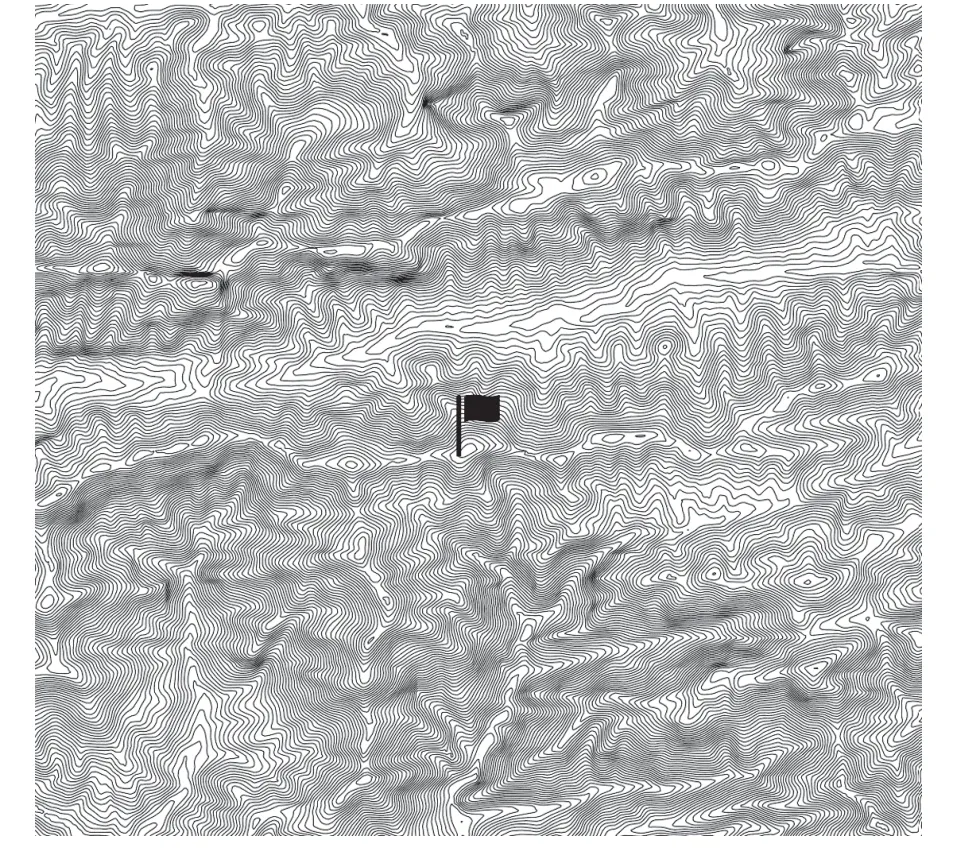
图2 观测塔2 海拔地形示意图（区域海拔范围1.5～2.5 km）Fig.2 Elevation topography of observation tower 2(regional elevation range: 1.5～ 2.5 km)

两座观测塔均使用的是美国NRG 公司Symphonie 型仪器，数据采集间隔10 min，观测不同高度的风速、风向、气温、气压、湿度等气象要素，如表1 所示，观测塔1 记录了9 m、10 m、30 m、70 m、100 m 的风速、风向和极大风速、极大风向，10 m、30 m、70 m、100 m 的气温，10 m 的气压以及100 m湿度，选取的观测时间段为2017 年1 月1 日至2017 年12 月31 日；观测塔2 记录了10 m、50 m、70 m、80 m 的风速、最大风速、最小风速和风速标准差，10 m、80 m 的风向、最大风向、最小风向和风向标准差，8 m、80 m 的气温以及8 m 气压，选取的观测时间段为2017 年1 月1 日至2017 年12 月31 日。

表1 观测塔1 和观测塔2 观测要素Tab.1 Observation elements of observation tower 1 and observation tower 2

2 大气稳定度及其计算与分类

大气稳定度是指大气稳定的程度。在大气边界层中，大气的热量主要来源于下垫面，动量主要来源于上层空气的流动，动量输送到底层，以补偿下垫面粗糙度引起的动量消耗。在近地面层，大气稳定度更多的是用来表征大气湍流的状态。大气稳定度表征参数有很多，相比于其他方法，莫宁-奥布霍夫长度法综合考虑湍流的热力作用和动力作用，物理意义也最为明确[15-17]。

莫宁-奥布霍夫长度法是莫宁与奥布霍夫提出来用以反映近地面层大气湍流状况的方法，简称M-O 长度法。M-O 长度法认为定常、水平均匀、无辐射和无相变近地面层的热力学和运动学结构仅由湍流状况决定，其论述了切应力和浮力对近地面层湍流输送的影响[18]。在应用气象学中，通常由梯度理查森数（Ri）来计算M-O 长度，即L 值。

当 Ri>0时，

当 Ri<0时，

对于梯度理查森数（Ri）的计算（近地层湍流通量计算及几种塔层风廓线模式的研究），一般来说，需要有两层高度的温度和风速观测。

式中：

g ——重力加速度（m/s2）；

∆T ——两层高度温度差（K）；

γd——是干绝热递减率（K/m）。

不同的 z1和 z2值可以计算出不同几何高度的梯度理查森数。

观测塔1 使用10 m、30 m、70 m、100 m 的气温和风速代入式（3）计算出梯度理查森数，再根据式（1）和式（2）计算出M-O 长度L；观测塔2 的10 m 观测高度没有气温记录，使用8 m 高度的气温观测作为替代，所以观测塔2 使用8 m 气温、10 m 风速、80 m 的气温和风速代入式（3）计算出梯度理查森数，再根据式（1）和式（2）计算出M-O 长度L。

针对莫宁-奥布霍夫长度法计算得到的M-O 长度L 值，需要有相应的稳定度分类标准对其进行帕斯奎尔-特纳尔稳定度类别（以下称“P-T”稳定度）划分[15]。Irwin[19]通过大量研究工作和实验数据拟合得到了地面粗糙度 z0和L 值之间的经验公式，即

根据GLC30 全球30 m 分辨率的地表覆盖数据，参考WASP 指南将其转换为地表粗糙度数据，提取出观测塔1 所在地表植被主要为耕地，所以取地面粗糙度 z0值0.03；提取出观测塔2 所在地表植被主要为灌木林地，所以取地面粗糙度 z0值0.25。再根据Irwin 稳定度分类标准计算公式得到L 稳定度分类标准如表2、表3 所示。

表2 观测塔1 的Irwin 稳定度分类标准Tab.2 Irwin stability classification criteria for observation tower 1

表3 观测塔2 的Irwin 稳定度分类标准Tab.3 Irwin stability classification criteria for observation tower 2

对两座观测塔分别计算所得的M-O 长度L 值，根据表2、表3 的分类结果进行划分，统计得到多个离地高度不同大气稳定度类别的占比，得到观测塔1和观测塔2 的大气稳定度分类结果如表4 和表5 所示。

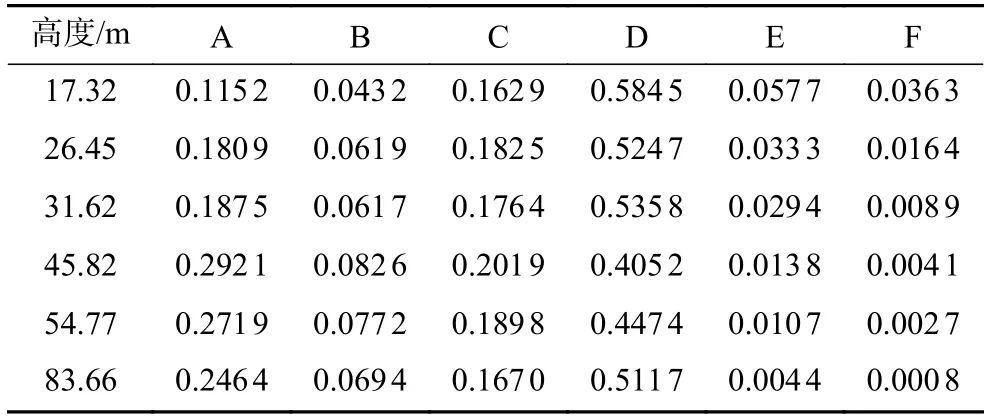
表4 观测塔1 的Irwin 稳定度分类结果Tab.4 Irwin stability classification of observation tower 1

表5 观测塔2 的Irwin 稳定度分类结果Tab.5 Irwin stability classification of observation tower 2

根据上述观测塔1 和观测塔2 稳定度分类结果分析，在约26 m 高度，观测塔2 的大气不稳定性明显要大于观测塔1，这很大程度上取决于观测塔2 所在的地形条件，在近地面层，复杂山地大气热效应造成的表层垂直混合作用更为明显，造成的大气不稳定性较为强烈；中性大气两者相差不大，且中性大气占比均为0.5 以上；观测塔1 较稳定和稳定的比重明显高于观测塔2。

对观测塔1 多层高度大气稳定度分类结果进一步分析，得到图3。稳定大气的比重随着离地高度增加而减少，不稳定大气和中性大气随着离地高度的增加有着完全相反的变化趋势，在离地约45 m 高度处不稳定大气和中性大气比重出现拐点，这高度以下不稳定大气随着大气热效应造成的垂直混合作用逐渐发展，到离地高度45 m 处发展到最旺盛，随着垂直混合作用发展稳定，中性大气在45 m 高度以上一直是增加的趋势。

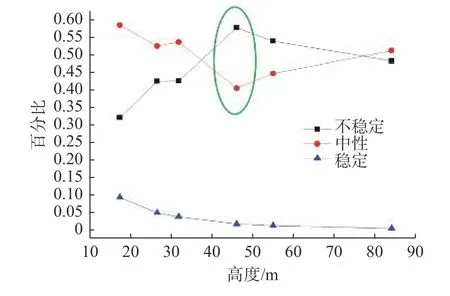
图3 观测塔1 大气稳定度随高度的变化Fig.3 Observation tower 1 atmospheric stability changes with altitude

3 两类下垫面大气稳定度对风机出力的影响

近地面层热力和动力的变化对风机出力产生着影响，对于平均年发电量（Annual Energy Production，AEP）来说，产生的综合影响主要是通过水平风的垂直变化。图4 和图5 分别是观测塔1 和观测塔2 大气稳定度分类结果对应的风速垂直变化，从垂直变化图看，观测塔1 和观测塔2 中性大气均为大风速值区，观测塔1 不稳定大气对风速的贡献要大于观测塔2 不稳定大气对风速的贡献，这个观测事实也在一定程度上说明以观测塔1 为代表的平坦地形近地面的大气热效应造成的垂直混合作用要比以观测塔2 为代表的复杂山地大气热效应造成的垂直混合作用要充分，在充分的大气热效应造成的热力作用和上层大气动力作用下传的共同影响下，观测塔1风切变指数要大于观测塔2，复杂山地由于不充分的大气垂直混合作用往往会造成近地面风速负切变的现象，但是受制于观测数据，此类下垫面垂直混合作用的拐点目前也没有更多的观测事实去研究和证实。

图4 观测塔1 大气稳定度分类对应的风速垂直变化Fig.4 Vertical change of wind speed corresponding to atmospheric stability classification in observation tower 1

图5 观测塔2 大气稳定度分类对应的风速垂直变化Fig.5 Vertical change of wind speed corresponding to atmospheric stability classification in observation tower 2

为了研究观测塔1 和观测塔2 大气稳定度对风机出力的定量影响，采用Gamesa G114-2.0 MW 风机功率曲线和推力系数曲线，使用风频法分别计算两座塔85 m 轮毂高度的发电量，分为考虑大气稳定度分类和不考虑大气稳定度分类两种情况，其中不考虑大气稳定度分类是目前工程应用上的普遍做法，计算得到表6。两座塔位置的发电量计算结果均是考虑稳定度的情况要高于不考虑稳定度的情况，观测塔1 高1.2%，观测塔2 高2.8%，从计算结果分析，复杂山地大气稳定度对风机出力的影响大于平坦地形，在工程应用中，随着复杂山地建设风电场越来越多，其风能资源分析与风机出力评估相较于平坦地形的不确定性要更强，所以在地形复杂的山地，更需要考虑大气稳定度的影响。

表6 考虑大气稳定度的风机出力计算Tab.6 Fan output calculation considering atmospheric stability

4 结论

大气稳定度是近地面层风速分布的重要影响因子之一。本文选取立于平坦和复杂山地两类典型地形上的两座测风塔不同高度的风速、气温、气压等观测数据，使用莫宁-奥布霍夫长度法分别计算两座测风塔所在区域的大气稳定度，参照Irwin 大气稳定分类标准对稳定度计算结果分类，再根据分类结果进行两座测风塔轮毂高度处出力分析，得到以下认识。

1）在近地面层，复杂山地大气热效应造成的表层垂直混合作用更为明显，造成的大气不稳定较为强烈；中性大气两者相差不大，且中性大气占比均为0.5 以上；观测塔1 较稳定和稳定比重明显高于观测塔2。

2）对观测塔1 多层高度大气稳定度分类结果进一步分析可知，稳定大气的比重随着离地高度增加而减少，不稳定大气和中性大气随着离地高度的增加有着完全相反的变化趋势。

3）以观测塔1 为代表的平坦地形近地面的大气热效应造成的垂直混合作用要比以观测塔2 为代表的复杂山地大气热效应造成的垂直混合作用要充分，在充分的大气热效应造成的热力作用和上层大气动力作用下传的共同影响下，观测塔1 风切变指数要大于观测塔2，复杂山地由于不充分的大气垂直混合作用往往会造成近地面风速负切变的现象。

4）随着复杂山地建设风电场越来越多，其风能资源分析与风机出力评估相较于平坦地形的不确定性要更强，所以在地形复杂的山地，更需要考虑大气稳定度的影响。

在工程应用中，特别是在复杂山地规划风电场时，建议前期立塔时设置多层高度的气温观测，以便于在进行CFD 计算时充分考虑大气稳定度的影响[20]，提高计算精度，从而减小风场投资风险。