基于EMD-MLP 组合模型的用电负荷日前预测
刘璐瑶 ,陈志刚 ,沈欣炜 ,吴劲松 ,廖霄
(1.中国能源建设集团广东省电力设计研究院有限公司,广东 广州 510663;2.清华大学 深圳国际研究生院,广东 深圳 518055)
0 引言
用电负荷日前预测对电力系统的运行优化起重要作用,其精确的预测结果是制定出合理、优质调度计划的基础。用电负荷预测方法主要有统计学方法和基于机器学习的方法2 种[1-4]。统计学方法基于自变量、因变量之间的统计规律进行预测,其中比较典型的有状态空间法[5]、线性回归法[6]、Box-Jenkins法[7]、自回归移动平均(ARMA)[8]、季节自回归(SA)[9]、季节自回归积分移动平均(SARIMA)[10]、门限自回归[11]等。统计学方法对于平稳性高、周期性强的用电负荷能够做出精确的预测。但是,当用电负荷受到天气等复杂多因素影响时,其数据表现出较强的随机性及非平稳性,此时,统计学方法难以获得有效的预测结果[12]。针对实际负荷数据具有的显著异方差、非平稳性,学者开发了自回归条件异方差(ARCH)[13]、广义自回归条件异方差(GARCH)[14-15]等方法。但是只有在检查了是否存在ARCH 效应后,才可以使用该类方法对时间序列建模预测[16]。因此,基于统计学的预测方法对负荷的非线性行为建模能力有限,灵活性不足。
针对非线性数据,人工神经网络(ANN)、深度学习(DL)等机器学习模型则可以更好地模拟异方差性,而不需要对数据做假设检验,表现出了更强的数据处理能力与更高的预测精度[17-18]。研究中用于用电负荷预测的机器学习模型包括:专家系统算法[19],灰色模型[20],模糊逻辑控制器[21],猫群算法优化的误差反向传播神经网络(CSO-BPNN)[22],多目标粒子群算法优化的BP 神经网络(MOPSO-BPNN)[23],蚁群优化的广义回归神经网络(ACO-GRNN)[24],粒子群优化的最小二乘支持向量机(PSO-LS-SVM)[25],深度置信网络(DBN)[26],长短时记忆循环神经网络(LSTM)[27-28],Attention 机制改进的LSTM[29],卷积神经网络(CNN)[30]等。以上机器学习模型通过对训练算法、模型结构参数进行优化,使得预测准确度得到一定程度的改善,但却缺少在预测之前对数据进行分解,导致预测精度仍有待提升[31]。
小波变换是一种有效的数据分解方法,研究[32-34]采用小波分解方法对原始用电负荷数据去噪,然后使用机器学习模型对剩余分量建模预测,获得了比未经小波分解的单一模型更高的预测精度。然而,不同的小波基函数其时频特性存在差异,因此对同一信号选用不同的基函数进行处理所得的结果往往差别很大,这增加了该方法在实际使用中的复杂程度[35]。学者们提出了经验模态分解(Empirical Mode Decomposition,EMD)、集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)及变分模态分解(Variational Mode Decomposition,VMD)等更高效的方法在预测之前对负荷数据分解[36]。孔祥玉等[37]采用EMD 将原始负荷数据分解为多个固有模态函数(IMF)分量,并采用基于最小二乘支持向量机(LSSVM)的方法对每个IMF 分量分别建立预测模型,最后将分量预测结果叠加得到最终预测值。邓带雨等[38]采用EEMD 的方法将原始电力负荷分解为多个IMF 分量,使用多元线性回归(MLR)和门控循环单元神经网络(GRU)对各分量分别进行预测并叠加,预测精度明显高于其他未经数据分解的单一预测模型以及基于小波变换的组合预测模型。梁智等[39]、刘雨薇等[40]采用VMD 技术与DBN、LSTM等模型结合以对用电负荷预测,与未采用数据分解的单一预测模型比较,MAPE 和RMSE 指标均有不同程度的改善。
现有将EMD、EEMD、VMD 与机器学习模型结合预测的研究,大多是对每个分量逐个预测,然后将各分量预测结果累加作为最终预测值。然而,在此过程中各分量预测误差会逐渐积累,导致最终的负荷预测误差增大。此外,由于分解分量较多,对每个分量分别预测导致了计算量繁重的问题,分量越多计算任务越繁重,这极大地限制了该方法的实际应用。因此,本文考虑对多分量进行重构,以精简预测对象、减少预测次数,以期在降低建模难度的同时提高预测精度。
本文提出一种将EMD 与MLP 结合预测的新方法,首先利用EMD 将原始用电负荷分解为多个分量,并采用极值点划分法将各个分量重构为高频和低频两个成分以精简预测对象,然后对二者分别预测并将它们的预测结果叠加作为最终的用电负荷预测值。利用澳大利亚电力市场(Australian National Electricity Market,NEM)多组实测电力负荷数据进行试验,对比分析验证本文方法在提高模型预测精度上的有效性。
1 EMD-MLP 组合模型
1.1 多层感知机
1)多层感知机原理
多层感知器(Multi-Layer Perceptron,MLP)为层级结构,包括输入层、隐含层和输出层。在MLP 中,各层神经元节点之间通过一定的权重连接,每个节点的输入由连接到它的前面各个节点的输出加权确定(输入层除外)。引入激活函数,对隐藏层中各节点输入进行非线性变换。通过多层叠加,MLP 可逼近任意连续函数,解决非线性回归问题。
MLP 神经网络训练过程的目标是通过调整激活函数、训练函数、隐含层数、隐含层神经元数量等超参数,找到使损失函数最优的权值和阈值集。
2)预测评价指标
为定量检验MLP 模型预测准确性,采用3 种预测评价指标:平均绝对误差、平均绝对百分比误差与均方根误差。
(1)平均绝对误差(Mean Absolute Error,MAE)是用来比较预测值和真实值之间绝对偏离程度的指标,表示为式(1):
式中:
Pf,t——t 时刻的用电负荷预测值;
Pm,t——t 时刻的用电负荷真实值;
N ——数据集样本数目。
(2)平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)是表征预测值与真实值之间相对偏离程度的指标,表示为式(2):
(3)均方根误差(Root Mean Squared Error,RMSE)是衡量预测值与真实值之间偏差离散程度的指标,表示为式(3):
1.2 经验模态分解
经验模态分解(EMD)是一种针对非线性非平稳信号的时频分析方法,由黄锷等人提出。EMD 理论认为任一复杂的时间信号是由若干个相互不同的本征模态函数(Intrinsic Mode Function,IMF)组成的,可采用一定的方法将复杂的时间信号分离成具有物理意义的从高频到低频的有限个独立分量,即基本时间信号。用电负荷时间序列可以看作是一种非平稳的信号,使用EMD 将负荷分解成多个基本信号,并分别采用多个模型建模可获得更准确的负荷预测结果。
EMD 过程中各个IMF 需要具备以下2 个要素:
1)在整个数据段内,极值个数与穿过时间轴的点个数相同或相差最多不超过1 个。
2)在数据段任何一处,由局部极大、极小值点形成的包络线均值为0。
用电负荷时间序列采用EMD 方法的分解过程如下:
首先,根据原始时间信号 X(t)的局部上、下极值点,得到 X(t)的上、下包络线。求上、下包络线的均值,得到均值线 m1(t) 。X(t) 与 m1(t)相减,则得到:
判断 h1(t)能否满足IMF 所需满足的2 项要求。若满足,则 h1(t)就是第1 阶IMF,若不满足,则以h1(t) 为基础,重复上述操作,得到 h1(t)的上、下包络线的均值线(t) 。h1(t) 减去(t),得到式(5):
式中:
从 X(t) 中减去 c1(t),得到频率较低的残差为 r1(t),表示为式(7):
将 r1(t)看成新的信号,按照上述操作,经过多次运算能够得到所有的 rj(t),表示为(8):
当满足条件“ cn(t) 或 rn(t)小于给定的误差”,或“残差 rn(t)为单调函数,不能再从中提取IMF”时,EMD 对时间序列的分解过程停止。X(t)最终分解成式(9)形式:
1.3 基于多分量重构的EMD-MLP 组合模型构建
本文提出的基于多分量重构的EMD-MLP 组合预测模型示意图如图1 所示,包含数据分解、分量重构、特征选择、模型训练与测试步骤。
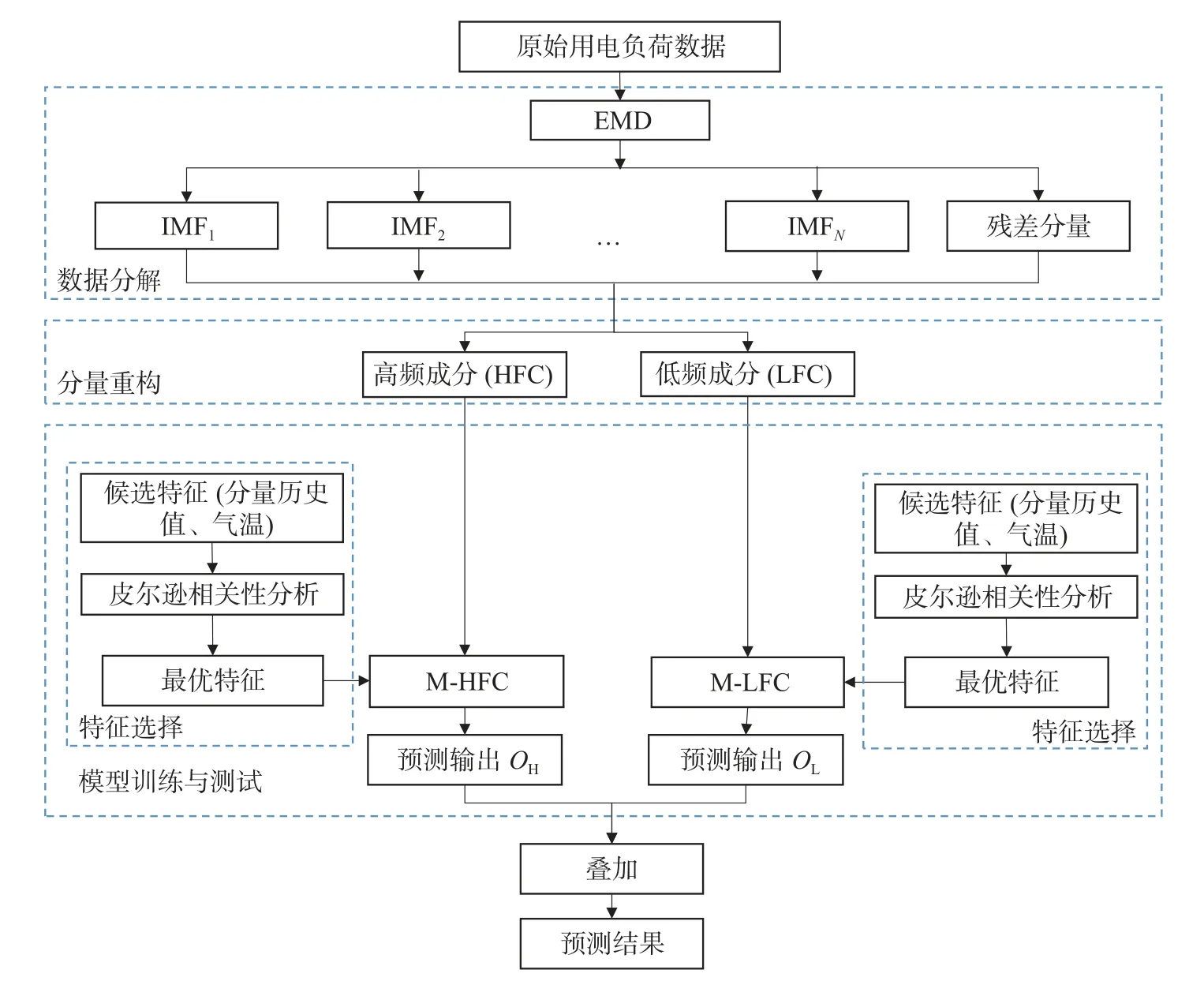
图1 EMD-MLP 预测模型示意图Fig.1 Schematic diagram of the proposed EMD-MLP combination model
首先,采用EMD 方法对原始用电负荷数据进行分解,形成多个本征模态分量(IMF1,IMF2······ IMFN,残差)。传统采用EMD 分解方法的预测模型对每一个分量分别预测,再将其结果叠加作为最终预测值。然而此方法存在一些问题,首先,对每个分量分别进行预测会导致建模计算量的增加;其次,对分量分别预测后进行叠加可能会引入预测误差的累积,从而限制了预测精度。
为解决这些问题,本文提出多分量重构手段,也即将经过EMD 分解后的分量根据其平稳程度进行划分,并进行重构。具体而言,对各模态分量采用极值点划分法进行划分,对划分后的分量进行叠加重构,形成高频成分(High Frequency Component,HFC)与低频成分(Low Frequency Component,LFC)。
使用MLP 模型对用电负荷数据中的高频与低频成分分别进行预测,建立的模型分别记为M-HFC,M-LFC。为了筛选出最优输入特征,采用皮尔逊相关系数法对候选特征进行分析。使用训练集对M-HFC,M-LFC 分别进行训练调参,优化模型结构。最后,使用训练好的模型在测试集上对用电负荷数据的高频成分和低频成分分别预测。将M-HFC,M-LFC 的预测结果 OH,OL等权值求和,得到用电负荷预测值。
2 数据处理
2.1 负荷数据分解及分量重构
本研究使用的负荷数据集从南澳电力市场获取[41],时间范围为2018 年1 月1 日至2018 年12 月31 日,以及2019 年1 月1 日至2019 年12 月31 日,每步15 min(如图2、图3 所示)。

图2 2018 年南澳用电负荷时间序列图Fig.2 Time series of electrical load in South Australia in 2018(step length: 15 min)
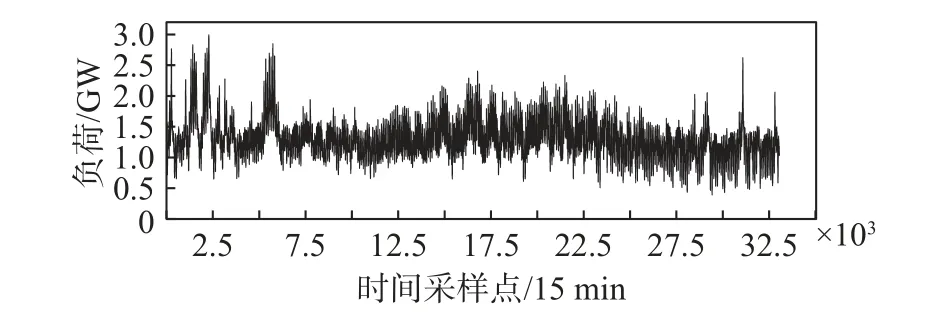
图3 2019 年南澳用电负荷时间序列图Fig.3 Time series of electricity load in South Australia in 2019(step length: 15 min)
基于2018 年、2019 年南澳原始负荷数据的EMD 分解结果分别如图4、图5 所示。
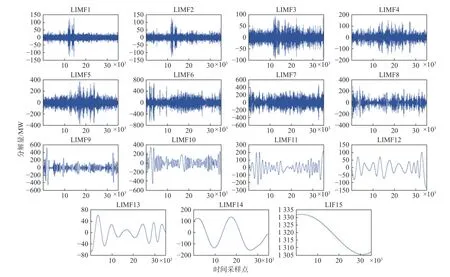
图4 原始负荷序列的EMD 分解结果(2018 年南澳用电负荷数据集)Fig.4 EMD decomposition results of original load series from South Australia in 2018

图5 原始负荷序列的EMD 分解结果(2019 年南澳负荷数据集)Fig.5 EMD decomposition results of original load series from South Australia in 2019
采用极值点划分法[42]对经EMD 分解后的各个分解分量进行重构。该方法首先求出各IMF 分量的极大、极小值个数,然后根据极值的个数对各IMF分量划分并重构。极值个数反映出分量的波动程度。基于极值点划分法将各分量重构为高、低频2 个成分。表1 给出了基于2018 年、2019 年南澳用电负荷数据得到的各分量极值点个数。选择一个合适的ρ作为区分高、低频成分的阈值,本文选择 ρ=100。因此,基于2018 年、2019 年数据,得到各分量中的IMF1-IMF9 重构后形成HFC,此成分波动频率较高,代表短期波动,IMF10-IMF15 叠加重构为LFC,此成分波动频率较低,变化平缓,代表长期趋势。各分解分量的重构结果如图6、图7 所示。
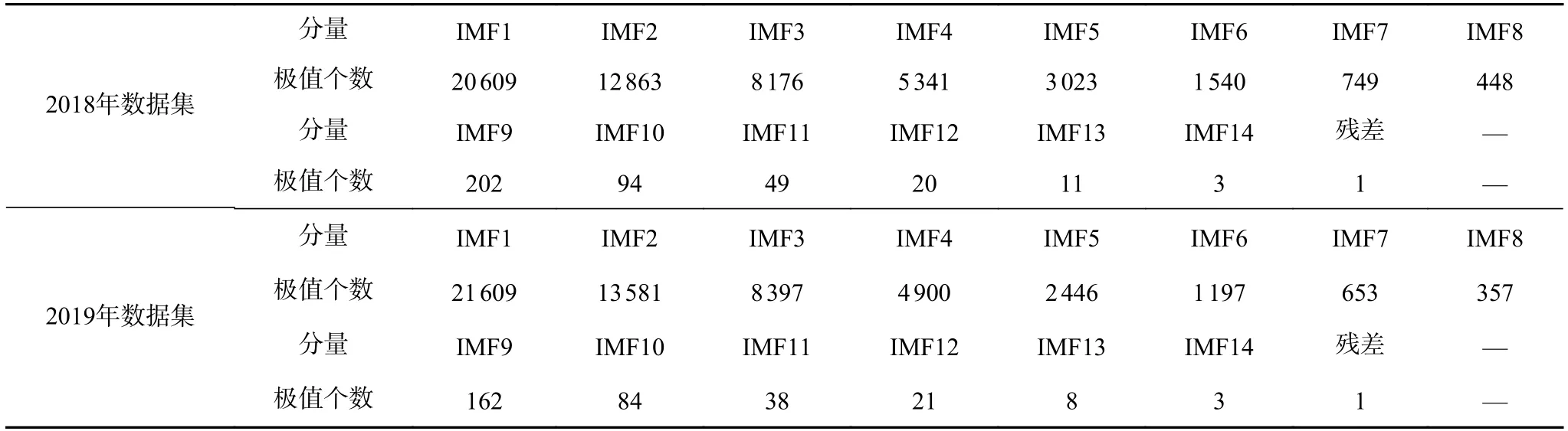
表1 各分解分量极值点个数Tab.1 The number of extreme points of each component
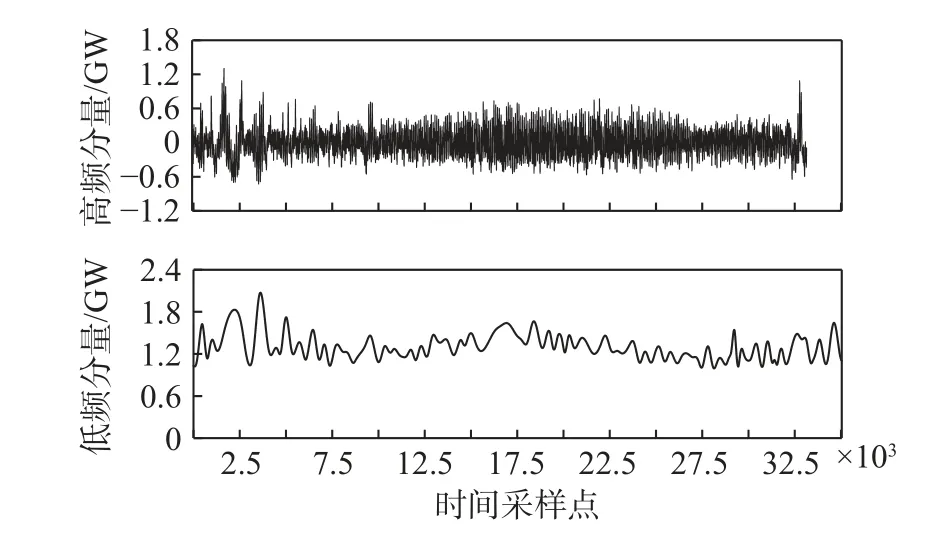
图6 2018 年南澳用电负荷的分解分量重构结果Fig.6 The reconstructed high-frequency and low-frequency components of electrical load in South Australia in 2018
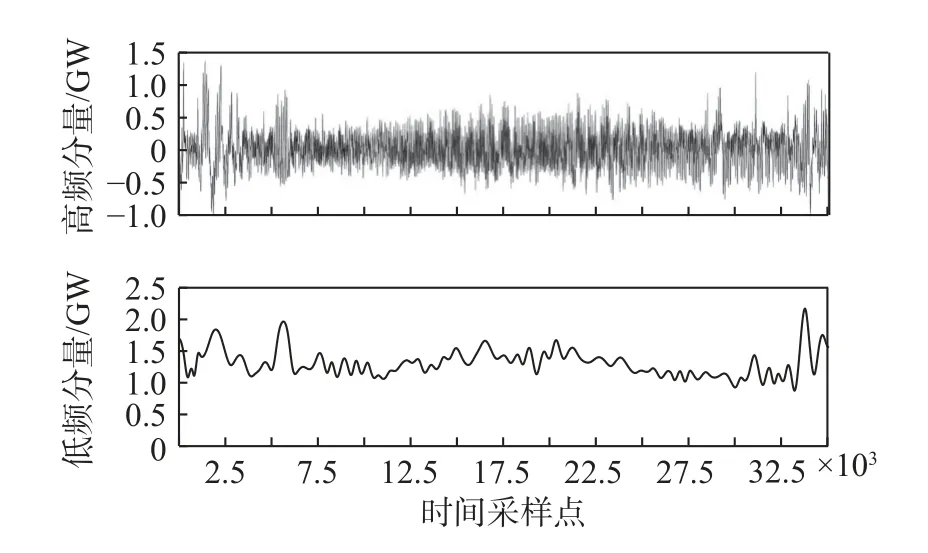
图7 2019 年南澳用电负荷的分解分量重构结果Fig.7 The reconstructed high-frequency and low-frequency components of electrical load in South Australia in 2019
2.2 基于皮尔逊相关系数法的特征选择
为了对d 日t 时刻用电负荷的高频、低频成分进行预测,首先分别选取他们的历史值作为候选输入特征[43-44],包含前1 日(d-1)至前7 日(d-7)同一时刻t 的历史值(记为)。
此外,一些天气因素,例如空气温度,也能影响到用电负荷的大小。本文采用预测日d 的日最高温度、日平均温度、日最低温度预测值(记为)作为另一组候选输入特征。使用的气温数据与负荷时间范围相同,为2018 年1 月1 日至2018 年12 月31 日 及2019 年1 月1 日 至2019 年12 月31 日。日最高、日平均、日最低温度数据为每天记录一次。2018 年与2019 年的南澳州阿德莱德市温度时间序列如图8、图9 所示。
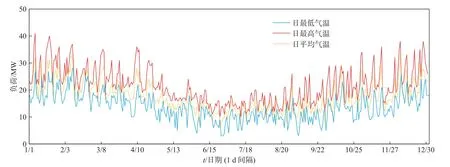
图8 2018 年南澳阿德莱德温度时间序列Fig.8 Temperature time series of Adelaide,South Australia in 2018

图9 2019 年南澳阿德莱德温度时间序列Fig.9 Temperature time series of Adelaide,South Australia in 2019
对于候选特征,采用皮尔逊相关系数法进行最优输入特征的选取[45]。皮尔逊相关系数用于度量输入变量x 和输出变量y 之间的线性相关性,其值介于-1 与1 之间。两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商,表示为式(10)。当相关系数为1 时,x 和y 完全正相关,当相关系数为-1 时,x 和y 完全负相关。相关系数的绝对值越大,相关性越强;相关系数越接近于0,相关度越弱。相关系数位于0.7~1.0 属于强相关,0.4~0.7为中等程度相关,0.2~0.4 为弱相关,0.0~0.2 为极弱相关或无相关。
式中:
rx,y——皮尔逊相关系数;
cov(x,y) ——x 和y 的协方差;
σx——变量x 的标准差;
σy——变量y 的标准差;
xi——第i 个样本的输入变量;
yi——第i 个样本的输出;
各候选特征与高频、低频成分间的相关性检验如表2 所示。选取相关系数绝对值大于0.4 的特征向量集合(加下划线标注),分别作为M-HFC 与MLFC 的最优输入特征。

表2 各候选特征与负荷高频、低频成分之间的相关系数(基于2018 年、2019 年南澳用电负荷数据训练集)Tab.2 Correlation coefficients between the candidate features and HFC,LFC (Based on the training data of South Australia electrical load in 2018 and 2019)
3 试验结果
试验中采用了2 份初始数据集,分别为2018 年1 月1日至2018 年12 月31 日及2019 年1 月1日至2019 年12 月31 日的南澳用电负荷及气温数据集。每份初始数据集划分为两个子数据集:前2/3 初始数据集作为初始训练集,后1/3 初始数据集作为测试集。初始训练集又进一步划分为训练集(前1/2 初始训练集)与验证集(后1/2 初始训练集),以确定预测模型超参数。测试集用来检测模型的泛化性能,不允许参与预测模型训练。
M-HFC 与M-LFC 的输入层、输出层神经元数目与相应训练集的输入、输出维数相等,根据表2,基于2018 年数据训练集的模型M-HFC 与M-LFC的输入层神经元个数为7 和3,输出层神经元数目为1 和1。基于2019 年数据训练集的模型M-HFC与M-LFC 的输入层神经元个数为7 和4,输出层神经元数目为1 和1。
M-HFC 与M-LFC 的最优超参数是通过在对应的训练集上训练得到的。需要调整的超参数有激活函数、训练函数、隐含层层数、隐含层神经元数目、学习速率、迭代次数、迭代目标。超参数的选取方法为,设定一个超参数调整范围/可选项,通过误差反馈迭代一定次数找到最优。MLP 神经网络的可选激活函数包括对数S 型函数,双曲正切函数,线性整流函数。可选用的训练函数包括小批量梯度下降法(Mini-Batch Gradient Descent,MBGD)、批量梯度下降法(Batch Gradient Descent,BGD,也叫最速梯度下降法)、随机梯度下降法(Stochastic Gradient Descent,SGD)、动态自适应学习率的梯度下降算法(Adaptive Gradient Descent,Adagad)等。隐含层数、隐含层神经元数目的调节范围分别为1~2 与2~100,学习率调节范围为0.01~0.1,迭代次数调节范围是100~2 000,迭代目标调节范围为0.000 01~0.01。基于2018 年、2019 年数据集的M-HFC 与M-LFC 模型在相应训练集上的最优超参数如表3 所示。

表3 M-HFC 与M-LFC 在相应训练集上的最优超参数(基于2018 年、2019 年南澳用电负荷数据训练集)Tab.3 Optimal hyper-parameters of M-HFC and M-LFC (Based on the corresponding training data from South Australia electrical load in 2018 and 2019)
为了验证本文提出的EMD-MLP 组合模型预测性能,在数据集上建立另外3 种模型,分别是持续性模型(PERSISTENCE)、单一MLP 模型(MLP)与传统EMD 组合模型(EMD-N)进行对比分析。持续性模型是最简单的预测模型,同时具有不错的预测性能,因而常常用作基准模型。持续性模型假设预测时刻的用电负荷 yt与预测窗口L 之前的用电负荷相同,将直接作为预测值,描述为式(11)。单一MLP 模型不经过EMD 分解,直接对用电负荷预测。传统EMD 组合模型首先将用电负荷经EMD 分解为多个分量,然后对各个分量分别预测,最后将所有分量的预测结果叠加作为用电负荷预测值。
基于2018 年、2019 年南澳电力负荷数据测试集,本文提出的EMD-MLP 组合模型与持续性模型、单一MLP 模型、传统EMD 组合模型的泛化误差箱型图如图10、图11 所示。结果显示,在4 种模型中,EMD-MLP 模型的预测误差不仅平均值更低,分布也更集中,表明本文提出的EMD-MLP 组合模型不仅可提高预测准确度,也具有更好的稳定性。图12、图13 为基于4 种预测模型的用电负荷预测值与真实值在局部测试集上的对比图,该图也显示EMDMLP 组合模型预测值与真实值更贴近。

图10 绝对百分比误差(APE),绝对误差(AE)与平方误差(SE)的箱型图(2018 年)Fig.10 Boxplots of APE,AE and SE based on the test dataset in 2018

图11 绝对百分比误差(APE),绝对误差(AE)与平方误差(SE)的箱型图(2019 年)Fig.11 Boxplots of APE,AE and SE based on the test dataset in 2019

图12 4 种模型负荷预测值与真实值对比(2018 年部分测试集:2018 年11 月1~10 日)Fig.12 Comparison of forecasted and actual values of load regarding the four models (part of the test dataset in 2018:Nov,1,2018~ Nov,10,2018)
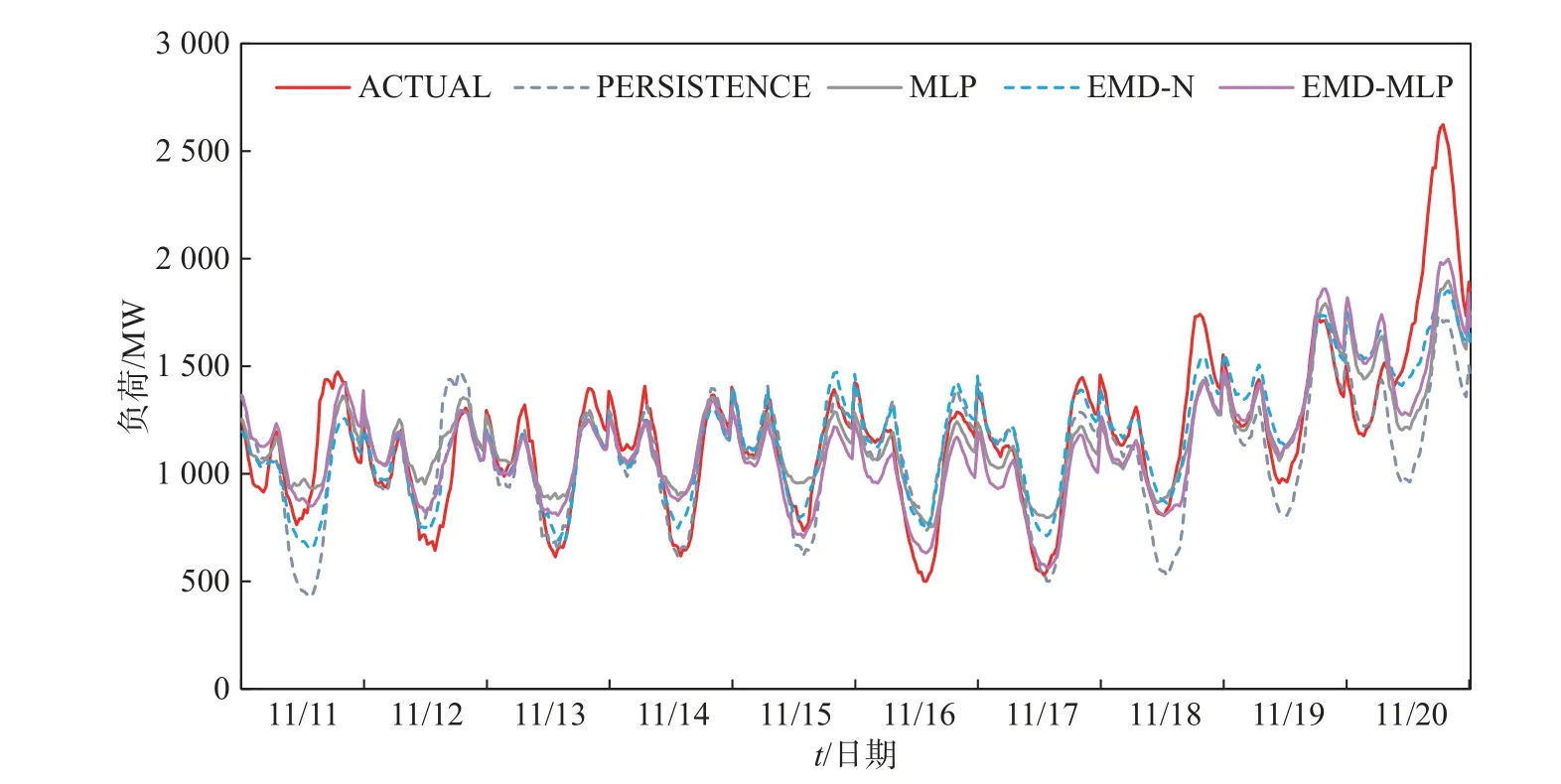
图13 4 种模型负荷预测值与真实值对比(2019 年部分测试集:2019 年11 月11~20 日)Fig.13 Comparison of forecasted and actual values of load regarding the four models (part of the test dataset in 2019:Nov,11,2019~ Nov,20,2019)
对误差箱型图10 和图11 中的绝对百分比误差、绝对误差在全测试样本上取平均值,对平方误差在全测试样本上取平均值再开方,得到4 种模型(EMDMLP 组合模型、持续性模型、单一MLP 模型、传统EMD 组合模型)的MAPE、MAE、RMSE3 个误差指标的结果。基于2018 年、2019 年数据测试集,这些误差指标结果如图14 所示。对于持续性模型,在2018 年、2019 年的数据集上,MAPE 分别为12.98%与15.68%,MAE 分别为148.5 MW 与173.7 MW,RMSE 分别为207.1 MW 与271.2 MW。而单一MLP 模型在这两个数据集上的MAPE、MAE 和RMSE 分别降至12.52%、137.6 MW、187.8 MW 以及14.68%、151.0 MW、206.7 MW。这证明采用多影响因素作为输入的MLP 相比简单的持续性模型可以提高预测精度,表明了采用MLP 建模的必要性。

图14 4 种模型在南澳电力负荷不同数据测试集上的预测误差(2018 年和2019 年)Fig.14 Forecast errors of the four models based on the test data of South Australia electrical load in 2018 and 2019
相比单一MLP 模型,EMD-N 和EMD-MLP 模型进一步提高了预测效果,表明将EMD 分解与MLP 结合进行预测的性能更具优越性。而与传统的EMD 组合模型相比,本文提出的EMD-MLP 组合模型预测精度更高。在2018 年和2019 年的数据集上,MAPE、MAE 和RMSE 分别进一步降低至10.60%、119.8 MW、157.3 MW 和12.37%、132.1 MW、179.5 MW。因此,本文提出的将EMD 与MLP 结合的新方法通过将EMD 分量重构后进行预测,避免了传统EMD组合预测方法中误差累加的问题,有效提高了预测精度。同时,本章提出的方法相比传统EMD 组合预测方法,能够实现数据压缩,极大地降低了计算量,提高了预测效率。
为了验证所提出模型的鲁棒性,选取另一场景下,即塔斯马尼亚电力市场2018 年、2019 年的用电负荷数据进行模拟。相应的用电负荷数据展示于附图S1、附图S2,空气温度数据展示于附图S3、附图S4。基于相应训练数据集选取出的模型最优输入特征见附表S1。经过训练后模型的最优超参数见附表S2。各模型在相应测试数据集上的泛化误差列于表4。结果显示,基于多分量重构的EMD-MLP 组合模型相比其他基线模型在MAPE、MAE 和RMSE上都表现出更好的泛化性能。
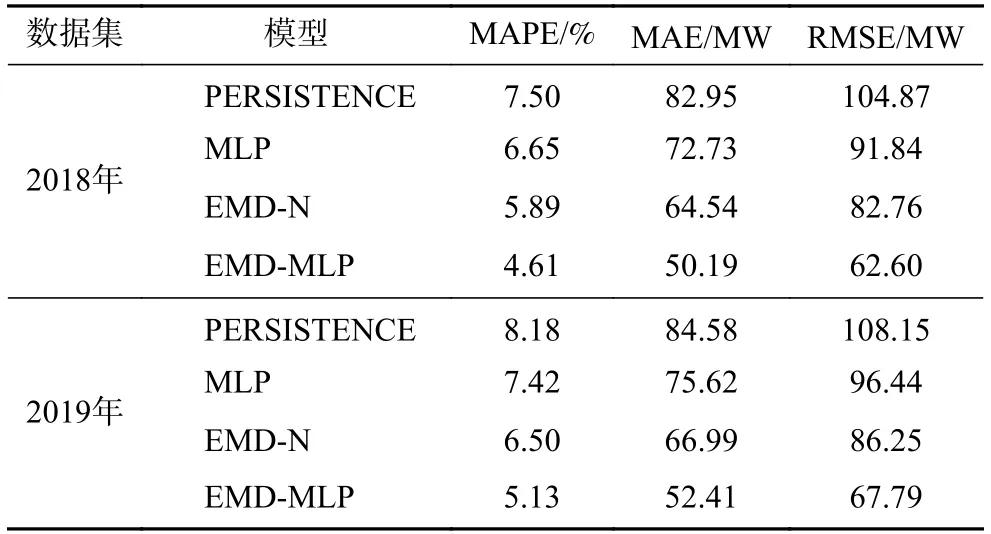
表4 各模型在塔斯马尼亚电力市场2018 年和2019 年用电负荷数据测试集上的泛化误差Tab.4 Forecast errors of different models on the test dataset of electrical load in Tasmania electricity market in 2018 and 2019
综上所述,本文提出的将EMD 与MLP 结合的新方法有效提高了预测精度,并且在不同数据集上具有鲁棒性,在用电负荷预测领域具有一定的使用价值与应用潜力。
4 结论
本研究提出了一种将经验模态分解与多层感知机结合用于电力系统用电负荷日前预测的新方法。该方法将原始负荷信号分解为多个本征模函数分量,并采用极值点划分法将这些分量重构为高频和低频两个成分,对它们分别建模预测并将其预测结果叠加作为最终的用电负荷预测值。为验证所提出的EMD-MLP 组合模型在提高预测精度方面的有效性,使用澳大利亚南澳以及塔斯马尼亚电力市场2018年和2019 年的实测用电负荷数据进行试验。通过与持续性模型、单一MLP 模型以及传统EMD 组合模型进行外推预测效果对比,所提出的EMD-MLP组合模型在泛化误差上表现最优,验证了该模型在用电负荷预测精度方面的优越性。
此外,本文所提方法将多分量重构合并为个数较少的分量并对这些分量进行预测,相比传统的EMD 分解后对各分量分别预测的方法,具有以下实际意义:(1)该方法通过精简预测对象减少了预测计算量与模型复杂度,提高了预测效率与模型可调节性,可以方便地在实际应用中进行日前、实时预测;(2)通过将分量合并为个数较少的分量,该方法减少了预测过程中的噪声和干扰,可有效提高预测模型的稳定性和准确性。因此,提出的EMD-MLP 组合预测新方法在电力系统能量管理中具有重要的应用前景,为实现电力系统的运行优化提供了可靠基础。
附录

图S1 2018 年塔斯马尼亚用电负荷时间序列图Fig.S1 Time series of electrical load in Tasmania in 2018 (step length: 15 min)

表S1 各候选特征与负荷高频、低频成分之间的相关系数(基于2018、2019 年塔斯马尼亚负荷数据训练集)Tab.S1 Correlation coefficients between the candidate features and HFC,LFC (based on the training data of Tasmania electrical load in 2018 and 2019)
(刘璐瑶)

