基于气象因素的长江经济带湖北段夏季日最大电力负荷预测

王丽娟 ，任永建 ，✉，王俊超 ，欧阳威

（1.湖北省气象服务中心,湖北 武汉 430205；2.中国气象局武汉暴雨研究所 暴雨监测预警湖北省重点实验室,湖北 武汉 430205）

0 引言

随着经济快速发展和人民生活水平不断提高，中长期电力负荷预测在电力安全和经济运行中至关重要[1]。影响电力负荷变化有多种不确定因素，包括经济发展、气象条件、人口等，总的来说，可以分为与气象相关和与气象无关两类[2]。电力负荷与气象要素之间有着密切的关系，并且近年来极端气候异常事件频发，严重影响电网的安全运行，2012 年7月30 日，在印度夏季发生的严重停电事故，异常高温就是导致事故的重要原因之一[3]。气象类因素对电力负荷与的影响越发引起广泛关注[4-6]，其中不少研究证明气温是影响电力负荷的重要气象因子[7-9]之一。早年研究[4]证明了华中电网日电力负荷在平均气温为25～28℃时对气温的变化最敏感。相关研究进一步证实北京、上海、南京、武汉地区的气温与电力负荷、日用电量之间存在比较明显的相关性。在此基础上，一些气象学者又基于气象因素对短期电力负荷的预测做了很多研究，傅新姝等[10]基于滤波技术，建立气象预报模型，采用逐步回归法，根据上海市冬季和夏季分别建立了日最大负荷的预测模型，预报年平均相对误差小于5%。李艳等[11]基于气温、炎热累积效应指数，建立了上海夏季日最大电力负荷预测模型，该模型采用SVR 支持向量回归方法及逐步回归，结果表明SVR 效果优于逐步回归法，最小平均相对误差仅为3.3%。任永健等[12]基于气象和电力负荷数据，来建立武汉市夏季最大电力负荷预测模型，采用双隐含层BP 神经网络及逐步回归算法，结果表明当气象因子对电力负荷的敏感性在10%以上时，能提高电力负荷预测精度。还有研究[13-14]证明，在考虑夏季气温累积效应的前提下，建立的电力负荷预测模型，精度能有所提高。

目前，研究工作[15-17]主要利用多个气象因子之间的关系或电力负荷或气象负荷与气温建立电力负荷预报模型，但气象因子对长期夏季日最大电力负荷定量预测分析不足，且预测时间一般比较短。本文利用气候模式预测气温对夏季日最大电力负荷定量预测，且预测时间较长，之前的研究较少涉及。本文基于气候模式预测的气温数据，综合利用灰色关联度、群粒子优化BP 神经网络算法及回归预测方法对长江经济带湖北地区3 个大中型城市(依据2022 年第7 次人口普查发布全国各城市城区人口情况，湖北省城市规模划定情况，人口50 万以上，为大中型城市)2020～2096 年夏季日最大电力负荷进行预测研究。

1 资料和方法

1.1 数据来源

本文选用武汉、黄石、宜昌3 个地区国家气象站2008～2019 年逐日最大电力负荷数据及同期平均气温、最高气温、最低气温、平均相对湿度等气象要素资料，夏季时段选择6 月1 日～8 月31 日。

本文中预测模式资料采用未来气候变化预测数据集由国家气候中心提供，是由CMIP5 全球气候模式HadGEM2-ES 的逐6 小时输出驱动RegCM4 区域气候模式，其中CMIP5 是一个由全球20 多个模式组50 余个模式组成，是最新的全球气候系统模式联合研究计划，通过动力降尺度试验应用于RegCM4区域气候模式，试验分别由CMIP5 中的4 个全球气候模式CSIRO-Mk3.6.0、EC-EARTH、HadGEM2-ES和MPI-ESM-MR 的历史试验结果驱动，分别记为CdR、EdR、HdR 和MdR。在动力降尺度模拟试验中，参数化方案参考了GAO 等[18]和HAN 等[19]的研究，水平分辨率为25 km×25 km，模拟的区域为区域气候降尺度协同试验中的东亚区域。并经过分位数映射法订正后的预测数据，模拟试验中采用的温室气体排放方案是中等温室气体排放情景RCP4.5。误差订正针对各个网格点的逐日序列进行，参照的观测数据使用格点化的数据来自基于中国2 400 多个站点观测资料插值而成的逐日气象数据集(CN05.1)，空间分辨率均为0.25°×0.25°。所用要素为平均气温，由于模式数据是格点数据，为更有效地与站点数据对比分析，利用双线性插值的方法，将模式格点数据插值到对应站点(武汉、黄石及宜昌)，时间段为1981 年1 月1 日～2096 年12 月31 日，时间尺度为逐日数据。预测负荷数据为日最大电力负荷。

1.2 气象敏感负荷

日最大电力负荷Lmax，如式(1)，可分为3 个分量。其中L0代表基础负荷，表示经济对电力负荷的贡献，相对稳定，随着经济的发展增加。L 代表气象敏感负荷，表示气象因素对电力负荷的影响，主要考虑气温、相对湿度及风的敏感。X 是一个不可预知的较小随机分量，代表随机因素对电力负荷的贡献。

在2008～2019 年的3～4 月选取日平均气温在15～20 ℃(此温度区间基本无敏感负荷)的日最大电力负荷，然后剔除包括检修、周末及节假日等情况下的少量异常数据，将剩余的日最大电力负荷值进行平均，即可得到基础负荷L0，共12 组数据，每组对应1 个年份的基础负荷值。由于随机负荷X 对日最大电力负荷影响较小且较复杂，可以在计算日最大电力负荷时忽略不计，如式（2）。

根据式(2)可得出日气象敏感负荷L，文中的日气象敏感负荷实际为日最大气象敏感负荷。2019 年夏季(6～8 月)武汉市、黄石市、宜昌市3 个地区日最大电力负荷为例，日最大电力负荷，基础负荷及气象敏感负荷3 者关系如图1 所示，3 个地区负荷变化规律不同，武汉市基础负荷最高，其次是宜昌、黄石。3 个地区的气象敏感负荷曲线与日最大电力负荷曲线变化趋势基本一致，由于气象因素对气象敏感负荷的影响更明显，后面分析各气象要素与气象敏感负荷的关系。

1.3 研究方法

1.3.1 灰色关联度

灰色关联度分析法相较传统的多因素分析方法，对数据的要求比较低且计算量较小，因此，广泛地应用到自然科学和社会的各个领域[20]。它是一种多因素统计分析方法，以各因素的样本数据为依据，若样本数据代表的两因素变化的趋势(方向、大小和速度等)都基本一致，则他们之间的关联度较大，反之关联度较小。进行灰色关联分析前，先对各数列进行无量纲化处理，即进行标准化处理：

式中：

xi——第i 个气象要素的样本平均值；

si——第i 个气象要素的均方差。

在进行标准化处理的基础上，设参考序列为日气象敏感负荷，其他列入指标体系中的序列即为比较序列(各气象要素)。利用式(4)计算比较序列各指标与参考序列各指标的关联系数。计算比较序列各指标对应于参考序列各指标的关联系数，根据排位次序即可确定各比较数列对参考数列的影响程度。设实际数据序列为x0，第i 种预测模型得到的数据序列为xi。

式中：

i ——比较序列个数（个）；

k——参考序列个数（个）；

ρ——分辨系数，ρ∈[0,1]，通常取ρ=0.5[21]，ρ 越小，分辨能力越强。

得出比较数列xi与参考数列x0的关联系数均值γi，如式（5）所示。

1.3.2 粒子群优化BP 神经网络算法及回归预测方法

粒子群算法（Particle Swarm Optimization，PSO）是一种基于模拟生物群体社会行为的智能优化算法。在PSO 中，问题的解被表示为粒子的位置，而粒子通过模拟个体与群体的协同寻优能力来更新其位置，以寻找最优解。和遗传算法一样，PSO 算法都是基于迭代模式的优化算法。在每次迭代过程中，每个粒子的位置目标函数都被评估。

粒子群神经网络是一种将粒子群算法应用于神经网络优化的方法。其基本原理[22]是利用粒子群算法来优化神经网络的初始参数，从而提高网络的训练速度和性能，以避免网络在训练过程中陷入局部最小值。用粒子群算法训练网络时，定义粒子群的位置向量Xi的元素是网络的全体连接权和阈值。首先初始化位置向量Xi，然后用粒子群算法搜索最优位置，使如下均方误差指标(适应度值)达到最小：

式中：

tjk——目标值（MW）；

fjk——计算值（MW）；

m——输出结点数（个）；

ns——训练集样本数（个）。

本文所构建的PSO-BP 神经网络模型如图2 所示。

本文根据日最大电力负荷变化历史数据及预测年份对应的日平均气温，采用二元线性回归分析模型，滚动预测未来日最大电力负荷，模型如下：

式中：

Ln——预测年份日最大电力负荷（MW）；

Ln-1——预测年份日前一日的最大电力负荷（MW）；

Tn——预测年份日的平均气温（℃）。

1.3.3 误差检验方法

采用绝对平均误差(MAE)和均方根误差(RMSE)作为评定预测好坏的标准。绝对平均误差计算公式为：

均方根误差计算公式为：

式中：

P′——预测值（MW）；

P ——实测值（MW）；

N ——样本数量（个）。

2 气象敏感负荷与各气象要素的关联性分析

首先，根据式(2)计算2008～2019 年武汉、黄石及宜昌3 个地区夏季(6～8 月) 日气象敏感负荷，并去掉敏感负荷为负或极小(小于10 MW)等非正常负荷值，剩余样本参与计算，其中非正常负荷数据占总负荷数据的10%左右。气象要素选取同期的平均气温、最高气温、最低气温、平均相对湿度进行计算。然后对气象敏感负荷及各气象要素进行无量纲处理，通过计算参考序列(日气象敏感负荷) 与比较序列(平均气温、最低气温、最高气温、相对湿度)之间的各指标的绝对差值(即关联系数)来看两序列的各指标之间的距离。由式(4)可见，差值越小，距离就越近，关联系数越大，反之亦然。

根据式(5) 计算灰色关联度，结果如表1 所示，可以看出这4 个气象要素中，武汉市平均气温与气象敏感负荷关联度最大，为0.620。黄石市平均气温与气象敏感负荷关联度最大，为0.729。宜昌市平均气温与气象敏感负荷关联度最大，为0.746。这3 个地区均是平均气温与气象敏感负荷关联度最大，即敏感负荷受到平均气温影响最大，其次是最高气温。从4 个气象要素进行关联度分析的结果看，其他气象因子的关联度较低，因此，在后面的分析中仅考虑温度因子。

表1 各气象要素与夏季气象敏感负荷的灰色关联度系数Tab.1 Grey correlation coefficients between meteorological elements and summer meteorologically sensitive load

3 日最大电力负荷预测

3.1 模式预测气温检验

在利用气候模式预测数据进行电力负荷预测之前，首先进行预测平均气温的检验。选取1980～2010 年30 a 武汉、黄石及宜昌的日平均气温实况及预测数据进行验证。本文评定预测好坏的具体算法见式（8）、式（9）。

通过对比30 a 武汉、黄石及宜昌的夏季(6～8月)、冬季(12～2 月)、年(1981～2010 年)、月(1～12月)预测的气温与实况的对比图可以发现，夏季预测数据与实况的拟合较好，明显优于冬季。预测的气温和实况在夏季、冬季及年变化基本一致，都是气温随时间上升趋势，其中年预测气温与实况拟合度较好。月预测气温与实况变化一致，都是夏季最大，冬季最小。进一步验证各项误差如表2 所示。

表2 预测平均气温误差统计Tab.2 Statistical analysis of prediction errors for average temperature

可以看出，夏季预测气温各项误差指标优于冬季，其中MAE 及RMSE 的值明显优于冬季，冬季预测的气温各项误差指标不如夏季；年、月预测气温MAE 及RMSE 的值比较接近。可见，模式预测气温各项误差指标总体较为理想。

3.2 基于PSO-BP 及回归法长期电力负荷预测及检验

选择神经网络隐含层为10 层，粒子个数为40 个，最大迭代次数为20 次，w最大值设为0.9，最小值设为0.2，c1 为2.5，c2为1。运用MatlabR2016b软件对PSO-BP 神经网络算法进行编程。根据设定参数，采用滚动预测方式对2020～2096 年夏季日最大电力负荷进行预测，每次预测30 d，前1 年6 月1日的预测值和6 月1 日当日的平均气温作为当年6月1 日预测的训练输入值，共滚动240 次。如图3所示，以2019 年为例，神经网络武汉预测误差指标MAE 为0.068，RMSE 为0.081。黄石误差指标MAE为0.042，RMSE 为0.051。宜昌误差指标MAE 为0.053，RMSE 为0.063。利用回归法建立预测模型，预测武汉误差指标MAE 为0.061，RMSE 为0.072；黄石误差指标MAE 为0.032，RMSE 为0.039；宜昌误差指标MAE 为0.038，RMSE 为0.047。

图3 基于PSO-BP 预测2019 年夏季日最大电力负荷(MW)与实况拟合关系Fig.3 Relationship of forecast result of summer daily maximum power load and fitted values in 2019 based on PSO-BP

3.3 预测结果分析

将2020～2096 年回归预测、神经网络预测的日最大电力负荷变化如图4 所示。可以看出，预测的日最大电力负荷的变化武汉呈线性变化，其他两地区呈非线性变化，为更好说明问题，将采用分段线性分析。从图4(a)看出，武汉日最大电力负荷年际变化，2020～2029年、2050～2059年、2080～2089年、2090～2096 年日最大电力负荷呈下降趋势，其他时间日最大电力负荷呈上升趋势。2020～2096 年武汉日最大电力负荷预测值在波动中总体呈上升趋势。从图4(b)看出，黄石日最大电力负荷年际变化，2020～2029 年、2040～2049 年、2050～2059 年、2070～2079年、2080～2089 年日最大电力负荷呈下降趋势，其他时间日最大电力负荷呈上升趋势。从图4(c) 看出，宜昌日最大电力负荷年际变化，2020～2029 年、2030～2039 年、2040～2049 年日最大电力负荷呈下降趋势，其他时间日最大电力负荷略上升。从以上结果可知，用回归及神经网络方法预测2020～2096 年黄石与宜昌日最大电力负荷预测值的变化趋势相似，武汉日最大电力负荷预测值变化趋势与黄石、宜昌明显不同，武汉市日最大电力负荷有较明显的上升趋势。

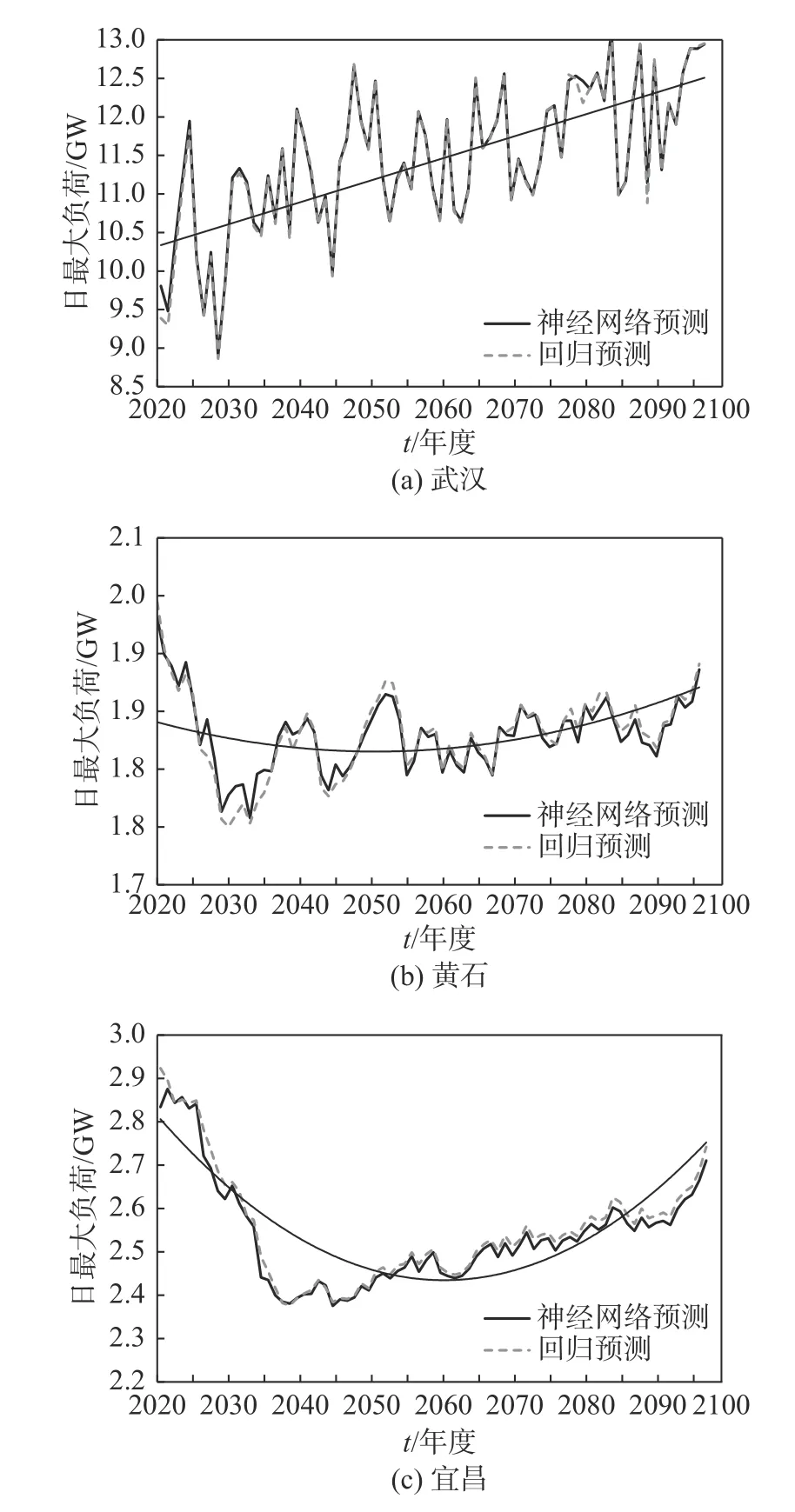
图4 2020～2096 年预测夏季日最大负荷（图中趋势线为神经网络预测）Fig.4 Forecast result of summer maximum load in 2020～2096(the trend line in the graph shows the neural network prediction)

图5 是武汉、黄石、宜昌3 个地区2020～2096 年回归预测、神经网络预测的日最大电力负荷距平变化。从图5(a)看出，近10 a 日最大电力负荷的最大值11.2 GW，武汉2020～2096 年日最大电力负荷两种预测值较近10 a 日最大电力负荷的最大值稳步增加，其中2080～2089 年日最大电力负荷增长率最高，超过17%，日最大电力负荷超过13.0 GW。武汉经济水平较其他两地区发达，日最大电力负荷已经达到较高水平，增长率比较稳定。从图5(b) 看出，较近10 a 日最大电力负荷的最大值2.1 GW，黄石2020～2096 年日最大电力负荷较其他两地区不同呈现下降趋势，2020～2029 年下降最少，其他年份日最大电力负荷在波动中下降，下降率在7%～11%之间。黄石经济水平不如武汉、宜昌两地，日最大电力负荷的预期值较其他两地呈现明显不同预测的结果。从图5(c)看出，较近10 a 日最大电力负荷的最大值2.0 GW，宜昌2020～2096 年最大电力负荷两种预测值都稳步增长，回归预测的增长率要略高于神经网络预测，其中2020～2029 年日最大电力负荷增长率最高，超过40%，接近3.0 GW。中间一段时间增长较平稳，从2070 年开始，日最大电力负荷增长率又逐渐变大，2090～2096 年日最大电力负荷增长率超过30%。

图5 2020～2096 年预测夏季日最大电力负荷距平Fig.5 Forecast result of summer maximum load anomaly in 2020～2096

4 结论

本文基于武汉、黄石、宜昌3 个地区2008～2019年逐日最大电力负荷数据及同期气象数据，以及RegCM4 区域气候模式预测数据，对以上3 个地区电力负荷特性进行分析，在此基础上利用粒子群优化BP 神经网络和逐步回归对几个地区未来(2019～2096 年)日最大电力负荷进行滚动预测，主要结论如下：

1)通过灰色关联度分析，在夏季，武汉市、黄石市、宜昌市3 个地区的平均气温与气象敏感负荷关联度均最大，即敏感负荷受到平均气温影响最大，其次是最高气温。

2)通过分时段检验模式预测气温数据，结果表明各项误差指标总体较为理想。基于PSO-BP 神经网络及回归法对3 个地区长期电力负荷预测结果，结果表明，武汉2020～2096 年两种预测值较近10 a的最大值稳步增加，日最大电力负荷超过13 GW。宜昌和武汉相似，两种预测值都稳步增长。黄石日最大电力负荷的预期值较其他两地呈现出明显不同结果。

本文在研究中，分离出的气象敏感负荷，很难完整地剔除城市基础负荷，此外气候模式预测数据精度与预测的负荷数据关系密切，气候模式精度限制了电力负荷预报的水平，这是本文的不足之处，也是以后研究的重点。与发达国家相比，国内需要将气候变化与国内的经济发展一并考虑。在这种情况下，有必要考虑气候变化作为电力消费的长期因素，以了解它对电力负荷增长的影响。考虑气温变化的条件下，研究更多不同地区电力负荷特征及预测来关注经济发展水平与气候变化的关系在以后的工作中需要进一步开展。

项目简介：

随着新能源的快速崛起，电网结构发生转变，且全球气候变暖带来的极端气候事件增加影响，不同区域电力需求变化及影响因子可能更加复杂。夏季连续高温天气，往往会使电力负荷达到最高值或突破历史极值，电网安全将受到严重影响。2017 年7 月下旬，武汉遭遇连续高温的侵袭，电网最大用电负荷急剧攀升，7 月23 日最大电力负荷超过10 GW，7 月28 日最大电力负荷达到最大值11 GW。2018 年夏季，受持续高温的影响，7 月16 至7 月27 日武汉日最大电力负荷连续超过10 GW，并于7 月26 日达到最大值11.3 GW，突破历史极值。基于气候模式和电网负荷-气象关系模型开展气候变化对电网负荷的影响评估是量化气候变化对行业影响的重要手段。本项目以长江经济带湖北段为研究对象，基于负荷分解算法，提取宜昌、武汉、黄石3 个城市气象敏感负荷；按相关标准给出的方法确定极端用电负荷日，分析负荷变化规律及极端用电负荷与气象要素的关系；基于分解的负荷数据和气象数据，建立电网极端负荷与气象因子的关系模型；选用RegCM4 动力将尺度预测数据，结合相关关系模型，预测不同排放情景下气候变化对极端用电负荷变化的可能影响；提出长江经济带湖北段电网极端负荷适应气候变化的对策建议。

项目名称极端事件对长江经济带湖北段电网负荷的影响

承担单位湖北省气象服务中心

项目概述主要研究内容包括：(1)得出长江经济带湖北段电网极端负荷与气象要素的关系及预测关系模型；(2)得出气候变化对极端用电负荷的影响；(3)提出研究区域极端用电负荷适应气候变化的对策建议。

主要创新点利用CMIP5 全球气候模式HadGEM2-ES 驱动RegCM4 区域气候模式进行动力降尺度，并经过分位数映射法订正后的预测数据结果，基于已建立电网负荷预测方程，开展了未来夏季日最大电力负荷的定量预测研究。