电力系统暂态稳定关键影响因素仿真研究

刘承峰，汤德威，康思扬，韦肖燕，唐勇奇

（湖南工程学院 电气与信息工程学院，湘潭 411104）

0 引言

随着经济的快速发展，我国电网规模迅速扩大，已形成了“西电东送”“北电南送”的电网大格局.尽管网架结构不断加强，但无法避免大扰动对电网的冲击和影响，三道防线建设对保证系统安全运行仍至关重要.针对三道防线中与暂态稳定密切相关的暂态电压稳定和暂态功角稳定问题，学者们进行了大量研究.文献［1］在单机无穷大的系统上探讨了感应电动机负荷参数对电力系统暂态电压稳定性的影响；文献［2］通过发电机与负荷之间的交互强度指标及暂态网络传输能力，分析了暂态功角和暂态电压的耦合强弱关系；文献［3］基于MATLAB 搭建的单机无穷大系统模型验证了系统故障切除时间及故障类型对系统稳定性的影响；文献［4］通过分析电压崩溃事故特征，明确功角失稳和电压失稳的区别和联系；文献［5］通过研究不同失稳模式与主导系统变量之间的关系，提出一种主导失稳模式识别方法.

综上，以往研究暂态稳定问题多以单机无穷大系统或单负荷无穷大系统作为分析对象，然而电网的复杂互联使得电力系统功角失稳和电压失稳时常相互耦合，此时相较单机无穷大或单负荷无穷大系统暂态过程更加复杂.本文以EPRI-36 节点的电力系统作为仿真研究对象，对不同感应电动机比例下暂态电压失稳及暂态功角失稳的耦合程度进行了计算和分析比较，并针对不同初始转差率和感应电动机比例对暂态稳定功角和电压主导失稳模式进行了仿真研究.

1 仿真模型及指标

1.1 仿真系统单线图

本文以EPRI-36 节点电力系统作为研究对象，在不同的感应电动机比例和不同转差率下，设置故障后系统失稳，通过该耦合强度和主导失稳模式相关指标的变化来进行深入分析.具体仿真设置为：负荷类型为感应电动机占比10%～90%，以20%步长改变的五种负荷类型；初始转差率分别设置为0.005、0.011 6、0.02、0.03 四种情况；故障时长为0.5 s；故障类型为三相短路接地.EPRI-36 节点电力系统单线图如图1 所示.

图1 EPRI-36节点电力系统单线图

1.2 负荷模型

采用经典三阶感应电动机模型，其微分方程如下：

式中，s0代表初始转差率、分别代表转子暂态电势d 轴和q 轴的分量；ω0是同步转速；Tj是转子惯性时间常数；是定子暂态开路时间常数；X和X'是定子漏抗和暂态电抗；id、iq是定子电流的d、q 轴分量；Te和Tm分别是电磁转矩和机械转矩.其中Tm可通过式（2）求出.

式中，KL代表感应电机的负荷率系数；α是机械负载转矩中与转速无关的部分所占比例；m是机械负载特性与转速有关的幂次.

1.3 暂态功角稳定性评估指标η

运用扩展等面积法中使用的失稳指标η［2］来评估功角稳定性.定义如下：

式中，Adec代表减速面积；Aacc代表加速面积；δmax代表随机两台发电机转子角度差值或发电机与母线节点的相角差值在发生故障后的最大偏离值.当最小减速面积小于加速面积时，则判断为系统功角不稳定，此时η＜0；当系统功角趋于稳定状态时，功角δ到达最大偏移位置后会发生回摆，此时减速面积等于加速面积，η=0.可以根据暂态稳定指标TSI判断发电机的稳定程度，取值范围为0～1，且越接近1 越稳定.

1.4 负荷稳定指标SL

感应电动机的初始转差率s0和端电压U决定着转子的运动状态，因此s0和U是判断电动机是否处于稳定状态的主要参考量.通常会从以下两个角度判断电动机的稳定性：

（1）当机端电压达到极大值或极小值时，转子最易发生加速或失稳.所以当机端电压处于最大值和最小值时刻，可通过转子运动趋势对感应电动机的稳定状态进行判断.

（2）初始转差率达到最大值或最小值时，此时转子最易发生加速或减速至堵转的现象.因此，在初始转差率处于极大值和极小值时，可通过转子运动趋势对感应电动机的稳定状态进行判断.

根据初始转差率和端电压的大小计算得到式（4）：

式中，t1表示故障切除时间，t2=max(tmax,tmin)；Te表示电动机的电磁转矩；Tm表示电动机的机械转矩；s0表示电动机的初始转差率；tmax表示故障切除后电动机端电压的极大值时刻；tmin表示故障切除后电动机端电压的极小值时刻.

式（4）中SL的分子与电动机单机势能函数相对应，也反映了发电机的动能.可以通过发电机转子运动方程得出

将式（5）两边同时乘以(1-s0)，得到方程两边的积分：

式中，SL的分母对指标进行了归一化，这使SL的范围在［-1，1］这个区间.当SL＞0 时，电动机的暂态稳定性处于稳定的状态，且稳定程度随着值越大越稳定；当SL＜0 时，电动机暂态稳定性处于失稳状态，且稳定程度随着值越小越不稳定.

在理解三种方法的意思时，部分学生出现困难：方法二和方法三，先求的是什么？后求的是什么？看着抽象的数量，学生眉头紧锁，睁着茫然的眼睛看着黑板。

1.5 耦合强度评估指标y1

上两个小节所采用的两个指标分别可以判断系统的暂态功角稳定性和暂态电压稳定性，接下来将采用文献［2］中发电机和负荷之间的交互强度指标y1判断两种暂态失稳状态的耦合强度.

将η在故障前动态负荷的灵敏度设为dη，SL在故障前发电机输出有功的灵敏度设为dSL.根据文献［2］中发电机与负荷强耦合的机理分析，将发电机和负荷之间的交互强度指标y1表示如下：

根据以往的经验，|y1|＜0.1 为极弱的耦合作用；|y1|∈[0.1,0.3]为较弱的耦合作用；|y1|∈(0.3,1]为较强的耦合作用；|y1|＞1 为很强的耦合作用.

2 动态负荷比例及初始转差率对暂态功角和暂态电压耦合程度的影响

2.1 动态负荷比例对暂态功角和暂态电压耦合程度的影响

将感应电动机占全网负荷的比例K分别设置为10%、30%、50%、70%、90%进行暂态稳定仿真，得到图2 关键发电机的暂态功角曲线和图3 的关键节点暂态电压曲线.以BUS1 和BUS8 的功角差和BUS16 的节点电压为例，由图2、图3 发现，当感应电动机占比为90%时，系统的功角在3 s 内会持续摆开将近9π（rad），电压跌落到0.2 p.u.～0.3 p.u.，此时系统出现功角和电压耦合失稳；将感应电机比例降到70%，功角在3 s 内会持续摆开将近8π（rad），电压跌落到0.5 p.u.～0.6 p.u.，发现功角摆开角度较感应电动机比例为90%时有所减小，此时系统失稳依然出现暂态功角和暂态电压的耦合；比例为50%时，功角在0～4/9 π（rad）之间波动，电压掉落到0.6 p.u.附近，此时系统的功角已较稳定，系统中主要出现的是电压失稳，暂态功角和暂态电压之间的耦合变弱；比例调至30%时，功角在0～1/3 π（rad）之间波动，电压跌落到0.9 p.u.；当比例为10%时，功角在0～1/3 π（rad）之间波动，电压基本恢复到故障前的状态，此时的系统处于一个较为稳定状态.表1列出了相应比例下暂态电压稳定极限切除时间tvc、暂态功角指标η、负荷稳定指标SL、耦合强度评估指标y1.当感应电动机比例为90%时，η最接近0，SL＜0，y1最接近1，此时系统同时存在功角和电压失稳，耦合程度最强，随着感应电机比例的减小，η逐渐接近1，说明功角越来越稳定，SL由负变正，且数值越来越大，说明电压越来越稳定，y1越来越小，说明两者之间的耦合程度越来越弱.

表1 感应电动机比例K对电压和功角耦合程度的影响

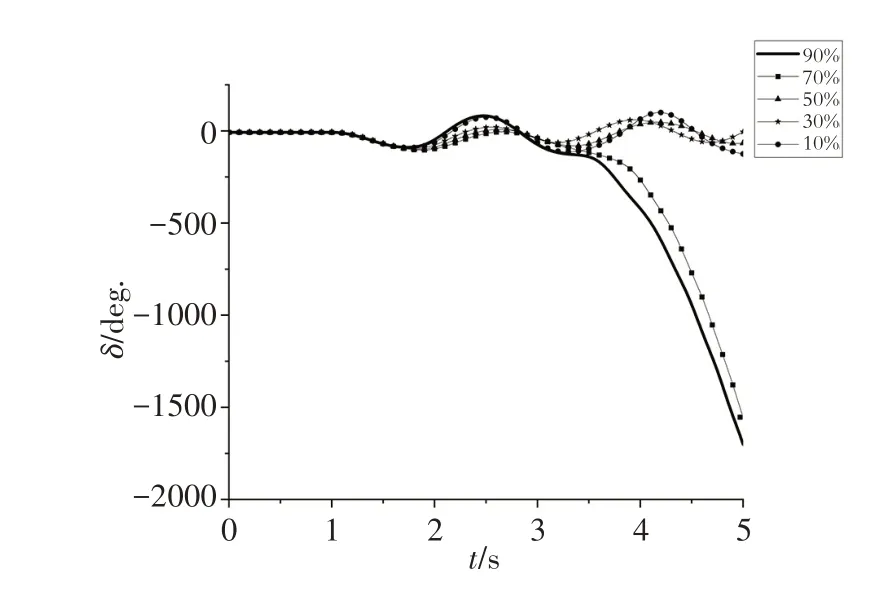
图2 不同感应电动机比例下的发电机功角曲线

2.2 初始转差率对暂态功角和暂态电压耦合程度的影响

调整系统感应电动机初始转差率进行暂态稳定仿真得到图4 关键发电机暂态功角曲线和图5 关键节点暂态电压曲线.选取BUS1 和BUS8 的功角差和BUS16 的节点电压为观察对象.如图4 和图5所示，当初始转差率为0.005 时，功角差持续增大到10 π（rad），BUS16 电压跌落到0.8 p.u.，此时系统同时出现暂态电压和暂态功角失稳；当初始转差率增大到0.011 6 时，功角差在0～2/3 π（rad）之间波动，电压跌落至0.7 p.u.，此时系统的功角已相对稳定，电压跌落更加严重；当初始转差率增大到0.020 时，功角差会在0～1/3 π（rad）之间波动，电压会跌落到0.6 p.u.，此时系统功角已经稳定，只出现电压失稳；当初始转差率增大到0.030 时，功角差会在0～1/3 π（rad）之间波动，电压跌落至0.3 p.u.，此时系统电压跌落严重，功角趋向稳定.

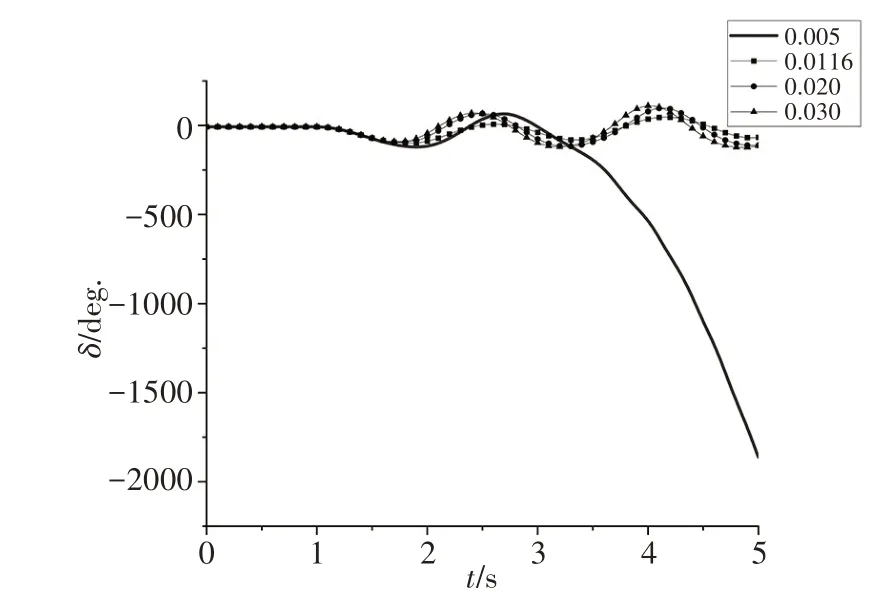
图4 不同初始转差率下的发电机暂态功角曲线

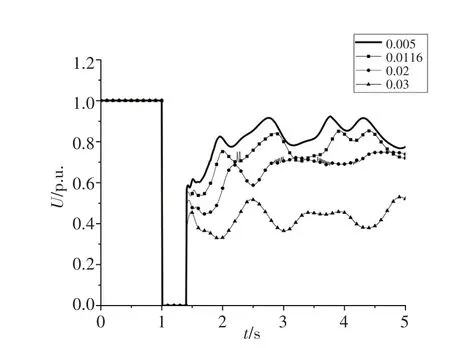
图5 不同初始转差率下的负荷电压曲线

表2 列出了四组初始转差率及相应的暂态功角指标η，负荷稳定指标SL，耦合强度评估指标y1.根据表2 的数据可知，当初始转差率增大时，η由负变正且越来越大，SL由正变负且越来越小，y1越来越小，说明随着初始转差率的增大，功角趋于稳定，而电压则更不稳定，此时电压和功角的失稳耦合程度逐渐减弱.

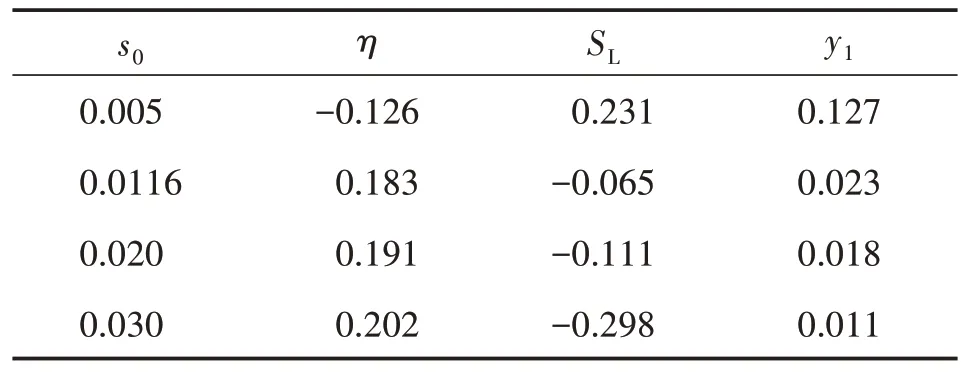
表2 发电机初始转差率s0对电压和功角耦合程度的影响

3 初始转差率和动态负荷比例对暂态主导失稳模式的影响

3.1 初始转差率对暂态主导失稳模式的影响

通过调整感应电动机初始转差率来观察在不同参数的数值下判断当前状态下的主导失稳模式.

由表3 可知，当初始转差率为0.005 时，主导失稳模式S小于0.5，此时的主导失稳模式为功角失稳；当初始转差率增大到0.011 6 时，主导失稳模式S大于0.5，此时的主导失稳模式为电压失稳，随着初始转差率继续增大到0.020 和0.030，S也始终大于0.5，主导失稳模式也为电压失稳，与2.2 节中的仿真结果相符.综上所述，随着初始转差率的增大，系统的主导失稳模式会从功角失稳转变为电压失稳.

表3 初始转差率s0对系统主导失稳模式的影响

3.2 动态负荷比例对暂态主导失稳模式的影响

从表4 中可以看到，随着感应电动机比例增大，主导失稳模式指标S始终大于0.5，可判断系统主导失稳模式为电压失稳.

表4 感应电动机比例K对系统主导失稳模式的影响

4 结论

在EPRI-36 节点电网仿真的基础上，通过调节感应电机的比例和初始转差率，分析了在暂态电压失稳和暂态功角失稳同时发生的情况下，其对电力系统的暂态电压和暂态功角稳定性耦合程度及主导失稳模式的影响.得出了以下结论：

（1）在电压和功角同时发生暂态失稳的情况下，感应电动机所占比例越大，暂态电压失稳和暂态功角失稳之间的耦合程度越强，初始转差率越大，则暂态电压稳定和功角稳定耦合程度越弱.

（2）在电压和功角同时失稳的情况下，主导失稳模式会随着初始转差率的增大，从功角失稳为主过渡到电压失稳为主.而随着感应电动机比例增大，主导失稳模式则一直以电压失稳为主.

研究的内容基于多机系统暂态稳定仿真，可对系统出现暂态电压和暂态功角同时失稳的情况下，感应电动机比例及初始转差率的影响提供一定的参考，并为暂态稳定紧急控制提供决策支撑.