基于EMD-AO-DELM 的光伏功率预测算法

曹 哲，赵葵银，王田宇，黄玮杰，司孟娇，林国汉

（湖南工程学院 电气与信息工程学院，湘潭 411104）

0 引言

光伏发电作为一种新能源发电，目前得到广泛应用.但受太阳辐射强度、温度、湿度和云量等因素的影响［1］，光伏发电波动性会影响光伏电力系统的安全性和稳定性，同时给光伏并网调度过程带来挑战.通过光伏发电历史数据对光伏发电功率进行预测，从而保证电网系统安全运行，这对完成电力系统调度十分重要［2］.

针对光伏发电功率的预测技术，主要分为直接预测方法和间接预测方法.前者是对光伏历史数据信息进行训练学习，通过预测算法进行未来功率预测.后者则采用分步预测的方式，可分为对未来日照辐射以及未来功率预测两个部分［3］.文献［4］提出一种基于经验模态分解（EMD）与极限学习机（ELM）组合功率预测方法，但未能充分考虑光伏电站输出功率受到的环境影响因素.文献［5］提出了一种基于烟花算法（FWA）的改进BP 神经网络光伏预测方法，该方法对于短期的光伏数据预测具有良好的精确度.但BP 神经网络存在收敛速度慢和易陷入局部极值的问题.文献［6］提出一种将卷积神经网络（CNN）和双向长短时记忆网络（BiLSTM）结合的预测算法，但该方法测试样本类型过于单一，未能测试不同季度及天气下的预测精度.

针对上述研究存在的问题，本文提出了一种基于经验模态分解（Empirical Mode Decomposition，EMD）—天鹰优化算法（Aquila Optimizer，AO）—深度极限学习机（Deep Extreme Learning Machine，DELM）的组合光伏功率预测模型.利用经验模态分解（EMD）将光伏初始功率数据分解为数量不同的本征模态函数（IMF），针对DELM 网络初始权重和阈值随机输入的特点，利用AO 优化算法对初始权重进行优化，利用优化的DELM 对每个模态分别建模预测，最后将各个模态分量的预测结果进行叠加求和，得到最终的预测结果.

1 理论基础

1.1 EMD（经验模态分解）

经验模态分解（EMD）［7-9］是一种基于信号局部特征的信号分解方法.其吸收了小波变换多分辨率的优点，克服了小波变换中选择小波基和确定分解尺度的困难，因此更适合于非线性非平稳信号的分析，是一种自适应的信号分解方法.EMD 假定任何复杂信号都是由简单的特征模态函数（IMF）组成的，并且每个IMF 之间是相互独立的.这种EMD可以将不同规模或趋势的时间序列数据逐步分解成其组成部分，并将一系列具有相同规模特征的数据序列产生一系列具有相同尺度特征的数据序列，通过这些数据序列，非平稳的非线性数据被转化为平稳的线性数据，与原始数据序列相比，分解后的序列具有更好的规律性.这对识别隐藏的关系有很大的帮助，可以提高预测的准确性［10-12］.

其具体分解步骤如下［13］：

（1）对于初始时间序列x(t)，取其所有极大值点与极小值点，所有极大值点相连作为上包络线，所有极小值点相连作为下包络线，记m(t)为上、下包络线的均值.令原始序列x(t)与均值m(t)相减，得到首个分量h1(t)=x(t)-m(t)；

（2）将h1(t)视作初始时间序列，记m1(t)为h1(t)的上、下包络线的均值，重复步骤（1），得到第二个分量h2(t)；

（3）将上述步骤不断重复n次，直到h(t)是一个本征模态函数或剩余分量rn(t)呈现单调性，终止分解过程.

至此，初始时间序列x(t)可通过n个本征模态分量hi(t)与一个剩余分量rn(t)之和来表示，如式（1）所示：

1.2 AO（天鹰优化算法）

Laith Abualigah 等人在2021 年提出的天鹰算法是一种新颖的元启发式优化算法，其灵感来自于北美洲的天鹰（Aquila）对不同种类猎物的四种狩猎行为.在攻击猎物之前，天鹰针对不同的猎物种类灵活地切换其狩猎策略.该数学模型简要描述如下［14］：

第1 步：扩大探索

天鹰在地面上高飞，广泛探索捕猎空间，一旦确定了猎物的区域，就会采取垂直俯冲的方式进行捕猎.这种行为的数学表示方法为

式中，Xbest(t)代表迄今为止获得的最佳位置；XM(t)表示当前迭代中所有天鹰的平均位置；t和T分别为当前迭代和最大迭代次数；N是种群大小；rand是0 到1 之间的随机数.

第2 步：缩小探索阶段

这是天鹰最常用的捕猎方法.它在选定的区域内下降并围绕猎物飞行后，采用短距离滑翔的方式来攻击猎物.位置更新公式表示为

式中，XR(t)代表天鹰的随机位置；D是维度大小；LF(D)代表Levy 飞行函数，其表示如下：

式中，Γ为伽马函数；s和β是分别取0.01 和1.5的常数；u和ν 是0 和1 之间的随机数；y和x用于呈现搜索中的螺旋形，其计算方法如下：

式中，r1是1 到20 之间的搜索周期数；D1由从1到维度大小D的整数组成；且ω=0.005.

第3 步：扩大开发阶段

在第三阶段中，当猎物的区域被大致确定后，天鹰垂直下降，进行初步攻击.天鹰利用选定的区域来接近和攻击猎物.这种行为的数字表示如下：

式中，α、δ是固定为0.1 的开发调整参数；UB、LB是上界和下界.

第4 步：缩小开发阶段

天鹰根据猎物逃跑的轨迹追逐猎物，然后攻击地面上的猎物.该行为的数学表示如下：

式中，X(t)是当前位置；QF(t)表示用于平衡搜索策略的质量函数值；G1表示天鹰在跟踪猎物过程中的运动参数，是［-1，1］之间的随机数；G2表示追逐猎物时的飞行斜率，从2 到0 线性递减.

1.3 ELM（极限学习机）

极限学习机（Extreme Learning Machine，ELM）的模型由输入层、隐含层和输出层三部分组成，是一个典型的单隐含层的前馈神经网络（Single-hidden Layer Feed-forward Neural Network，SLFN），其网络具有学习速度快、泛化能力强等优点［15］.

ELM 的模型结构如图1 所示，其中，输入层含q个节点，隐含层含n个节点，输出层含e个节点，隐含层激活函数为g(x)，常用的函数有sigmoid、hard-lim、sin 等［16］.

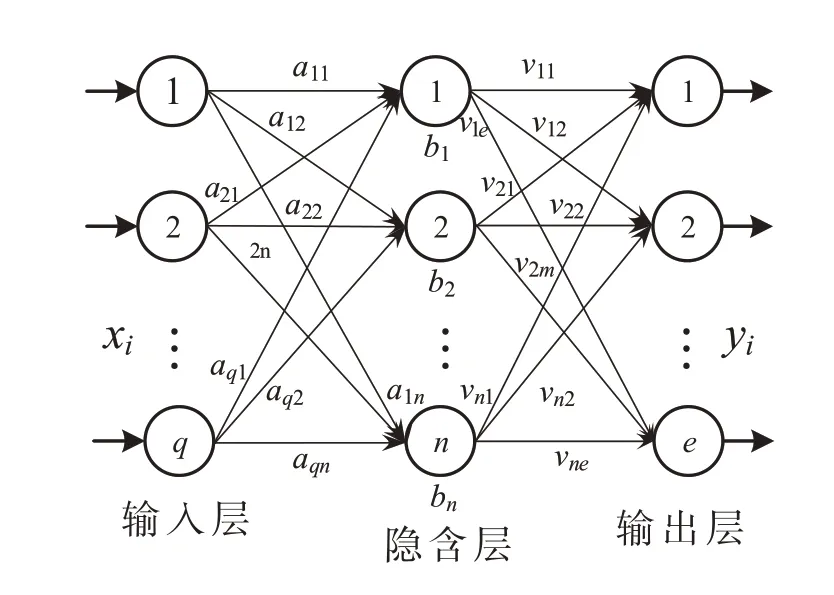
图1 ELM结构

假设样本为xi∈RN×Rq，yi∈RN×Re(i=1,2,…,N)，其中，隐含层的输出为式（9），隐含层输出矩阵和ELM 网络输出之间的关系可由式（10）表示.

根据式（9）和式（10），有

其中，ai=(ai1,ai2,…,ain)T是连接第i个输入节点和隐含层的权重；bi是第j个隐藏节点的阈值；νi=(νj1,νj2,…,νjn)T是连接第j个隐藏节点和输出层的权重；H是神经网络的隐含层输出矩阵.输入权重aij和隐含层的阈值bj随机选取；输出权重V可以通过解方程组的方式得到［17］.

使用ELM 获得输出权重可以分为三个步骤：

（1）随机选择0 和1 之间的数值来设置输入权重aij和隐含层的阈值bj；

（2）计算隐含层输出矩阵H；

（3）计算输出权重V：

其中，H+表示输出矩阵H的广义逆矩阵.

与传统的基于梯度的前馈神经网络算法不同，极限学习机网络隐含层在训练过程中随机产生输入权重和阈值.因此，计算输出权重只能采用广义逆矩阵理论.而ELM 是一种单隐层结构，在面对数据量大且维度较高的输入数据时，其捕捉数据的有效特征的能力不足.因此，更多学者采用DELM 算法，作为ELM 的一种衍生算法，DELM 解决了只有一个隐含层的极限学习机无法捕捉数据的有效特征的问题.

1.4 ELM—AE（极限学习机—自动编码器）

极限学习机自动编码器（ELM-AE）是一个人工的神经网络模块，在深度学习领域中得到广泛使用，是一种无监督方式学习样本的结构.其主要特点在于网络的输出和输入结果一致.ELM-AE 的模型如同ELM，同样由一个输入层、一个隐含层和一个输出层三部分组成［18］，其模型结构如图2 所示.构建的ELM-AE 在训练过程中隐含层节点的权重和阈值随机产生，并具有正交性，从而使得ELMAE 的泛化能力得到了一定程度的优化.为进一步提高模型的泛化能力和鲁棒性，在求解权重系数的过程中引入正则化参数，目标函数被设定为［19］

假设给定N个不同的样本，xi∈RN×Rq(i=1,2,…,N)，ELM-AE 隐含层的输出可以表示为式（15），那么隐含层的输出矩阵与输出层的输出之间的数学关系可以表示为

对于等维ELM-AE 表示，输出权重V的计算方法是：

其中，H是ELM-AE 隐含层输出矩阵；X是ELM-AE 的输入矩阵.

深度极限学习机（DELM）通过叠加极限学习机—自动编码器（ELM-AE）构建多层网络结构来提高网络的表达能力，是极限学习机和自动编码器结合的新结构.

DELM 应用ELM-AE 对模型进行逐层训练.i隐含层的输出与(i-1)隐含层的输出之间的数值关系可以表示为

1.5 DELM（深度极限学习机）

ELM-AE 用于构建深度极限学习机DELM 的基本单元，然后利用ELM-AE 的输出权值初始化整个DELM［20］.DELM 的理念是通过最小化重建误差使输出无限接近于原始输入，通过层层迭代训练，学习原始数据的高级特征.

ELM-AE 在编码器处将输入映射到隐含层特征向量，在解码器处从特征向量重建原始输入［20］.从结构的角度看，DELM 相当于连接多个ELM.与ELM 相比，DELM 能更全面地捕捉样本特征，提高处理高维输入的准确性.DELM 通过ELM-AE 逐层进行无监督训练和学习，最后连接到最后一层输出层进行有监督训练.该系统的参数不需要同时调整［21］.DELM 网络的结构如图3 所示，DELM 各隐含层的输入权重通过ELM-AE 初始化，并进行分层无监督训练.在这整个过程中，DELM 不需要反向微调.

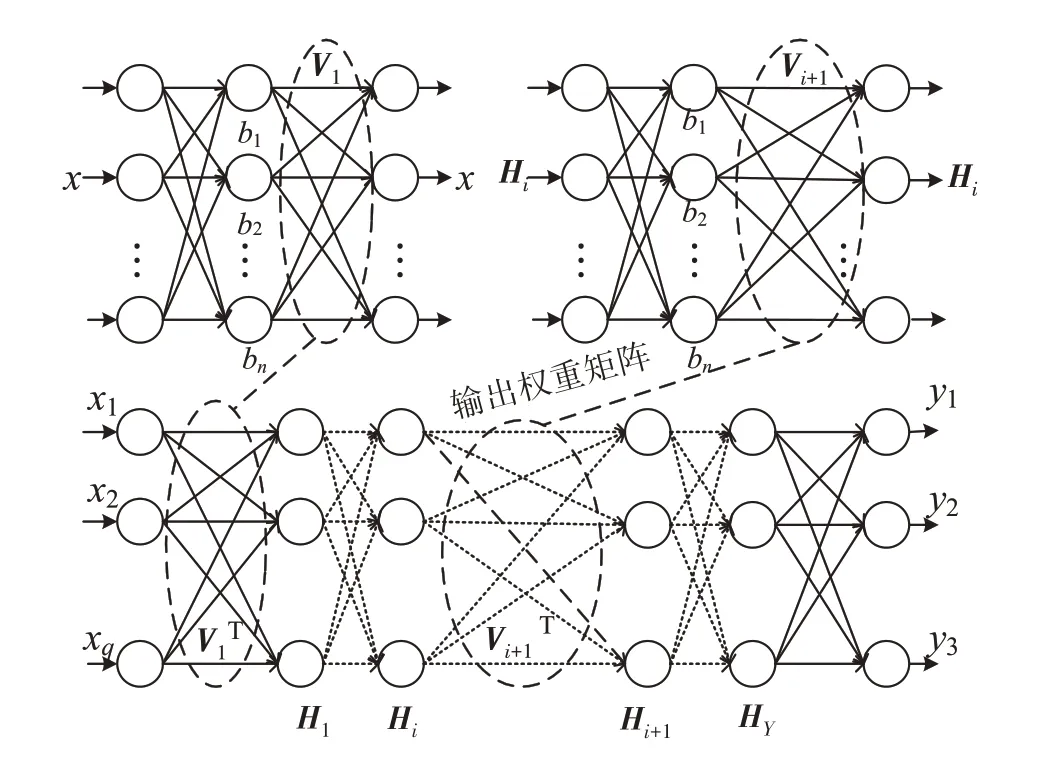
图3 DELM结构图

假设在模型有Y个隐含层的情况下，根据上文所述ELM-AE 理论，通过输入数据X可以得到权重矩阵V1与隐含层的输出矩阵H1.将H1作为下一个ELM-AE 的输入与目标输出.以此类推，逐层训练，可以得到Y层的输出权重矩阵VY和隐含层的输出矩阵HY.其中每个ELM-AE 的输出权重用来初始化整个DELM.在ELM-AE 训练过程中，输入层权重和阈值是随机生成的正交随机矩阵；同时，ELM-AE 无监督训练过程采用最小二乘法更新参数.在这个过程中，只有输出层权重参数被更新，而输入层权重和阈值保持不变，每个ELM-AE 的随机输入权重和随机阈值都会对DELM 的预测精度造成影响.由于初始权重对于整个模型的预测结果起到更关键的作用，因此，本文针对DELM 的输入权重利用AO 算法进行优化.

在本文中，利用天鹰优化算法的全局优化能力，可在训练误差较小时找到深度极限学习机的输入权重，从而提高深度极限学习机的泛化能力，提高DELM 的预测精度.

2 EMD-AO-DELM 预测模型的建立

2.1 光伏发电影响因素分析

光伏发电效率的影响因素众多，主要分为主观因素和客观因素.其中，主观因素包括气温、湿度、云量、降水量、光照辐射度等不可控的气象因素；客观因素包括光伏阵列安装地形条件、光伏板倾角与朝向等，往往起到决定性作用的是气象因素［22］.输入样本因素过多会降低预测精度并使预测模型变得复杂和冗余.为探究气象因素与光伏功率的相关性，以便选取最优因素作为输入，在此处引入Pearson 相关系数，用来衡量两个数据集合是否在一条线上，并衡量定距变量间的线性关系.

式中，r＞0 表示两者之间呈正相关，r＜0 表示两者之间呈负相关；xi与yi分别代表两个因素第i个的值；xˉ和yˉ分别表示两个因素的平均值.

根据Pearson 相关系数，整理出表1.

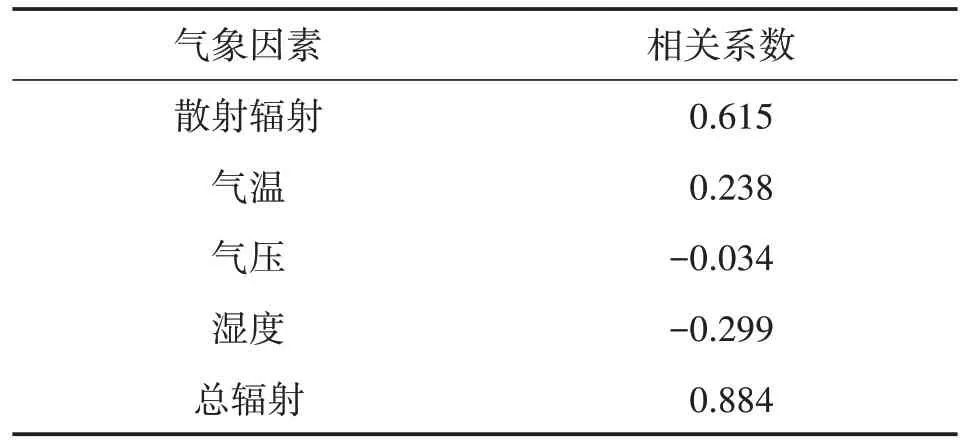
表1 各气象因素相关系数

由表1 可知，光照总辐射和散射辐射与光伏功率呈现高度正相关，相对湿度和大气压与光伏功率呈现负相关，因此，选取散射辐射和总辐射这两项作为DELM 初始输入数据.

2.2 AO-DELM模型的建立

AO-DELM 模型的主要思想是：将DELM 初始输入权重作为AO 算法的初始种群位置，并将适应度函数设置为训练集和测试集的均方误差之和，其表示如下：

AO-DELM 预测模型流程如下：

（1）进行数据清洗，将历史光伏功率数据中一些采样时发生错误导致的异常值剔除；

（2）对清洗后的样本数据进行归一化处理；

（3）初始化AO 算法参数，包括种群规模，最大迭代次数T，探索和开发参数α、δ；

（4）初始化种群位置X、初始的种群适应度、最佳个体；

（5）按序进行扩大探索阶段、缩小探索阶段、扩大开发阶段、缩小开发阶段，并不断更新种群位置；

（6）计算更新种群的适应度，得到当前最佳个体位置和适应度，并比较当前最佳个体与到第t代找到的最佳个体适应度，保留较优的个体位置；

（7）判断是否达到最大迭代次数或者求解条件，若是，则输出最优值，若否，则返回步骤（5）；

（8）将最后优化后的权重值结果输入到DELM模型中.

其结构流程图如图4 所示.

图4 AO-DELM结构流程图

2.3 EMD-AO-DELM 模型的建立

光伏功率数据是非线性非平稳的离散数据，传统线性时序模型方法存在较大的局限性，直接对其进行预测建模具有较大的误差.因此，采用EMD 对光伏发电功率曲线进行分解，从而将原始环境信号中存在的不同尺度波动或趋势逐级分解出来.对分解后的IMF 分量分别进行AO-DELM 建模分析，再将各IMF 分量预测结果进行叠加求和得到最终的预测值［22］.

具体步骤为：

（1）采用EMD 对光伏历史数据进行分解，得到一组IMF 分量；

（2）将各IMF 分量分别建立AO-DELM 模型，对各个分量进行预测；

（3）叠加各子序列的预测结果并验证模型预测的准确性.

采用EMD 方法将光伏历史数据分解为n个不同特征的IMF 分量以及一个余量Res，其中5 月份各IMF 序列如图5 所示.IMF 分量能够体现出原始数据的局部特征，更好地反映其周期项、随机项以及趋势项，准确反映出原始数据的特性.

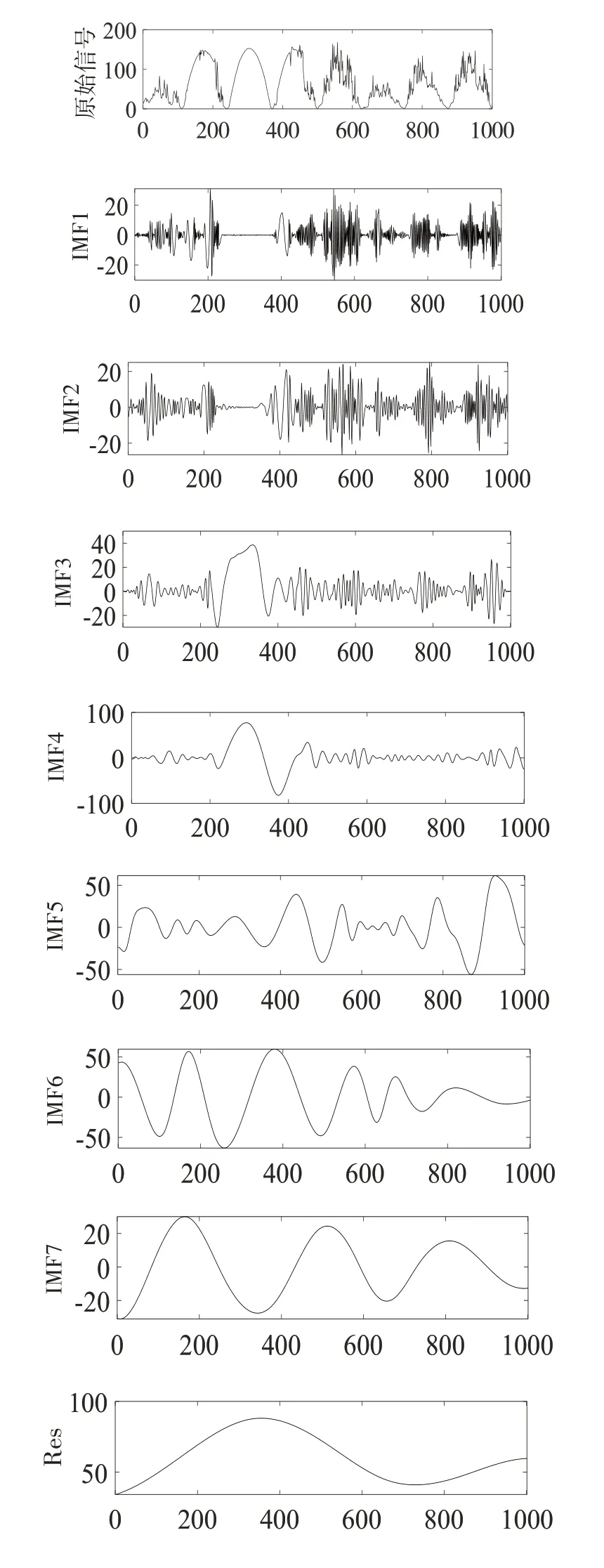
图5 EMD分解序列

其中，IMF1-IMF5 呈现不平稳、振荡的曲线，属于随机项；IMF6-IMF7 呈现平滑、频率降低、周期性的趋势，属于趋势项.因此，EMD 分解可凸显原始光伏发电功率序列局部特征.EMD-AODELM 预测模型流程图如图6 所示.

2.4 评价指标

为了验证本预测模型的有效性与准确性，采用MAPE与RMSE两者作为误差指标.

式中，yoi是样本中第i个真实值（observed）；ypi是样本中第i个预测值（predicted）.两者数值越小，精度越高.

3 实例分析

本文的样本数据均采集于青海某光伏电站，采集5月份共31天光伏输出功率数据，采集步长为5 min.

3.1 异常数据清洗

在光伏电站实际采样过程中，会产生一些异常数据.异常数据会导致预测模型拟合度变差、泛化能力减弱.因此，必须对其进行清洗.

对异常数据的检测采用3σ 准则原理：

式中，X表示光伏功率初始数据；表示光伏功率初始数据平均值.

在统计学上，3σ准则是在正态分布中距平均值小于一个标准差、二个标准差、三个标准差以内的百分比，更精确的数字是68.27%、95.45%及99.73%.

3.2 数据归一化

不同数据单位量程不一，这对模型的拟合速度造成影响，且不利于模型训练.为提升模型预测精度，对初始光伏功率数据进行归一化，将归一化后的功率值保持在［0，1］.其中，归一化公式如下：

式中，yi代表归一化后的数据；xi代表原始功率数据值.

3.3 仿真结果

本文采用MATLAB R2022a 对所提出控制策略进行仿真分析，在本文所建立的预测模型中，设置DELM 模型隐含层层数为2；隐含层节点数分别为5，5；AO 最大迭代次数为200；种群数量为20；正则化系数设置为无穷大.公平起见，作为对比的DELM 模型参数隐含层层数为2；隐含层节点数分别为5，5.

将5 月数据按19∶1 分别划分为训练集和测试集，并进行归一化处理.其中测试集取每日8 点至19 点，日出之后时间段晴天和复杂天气各一天，分别进行仿真验证，步长为5 min.

预测仿真结果如图7 所示.

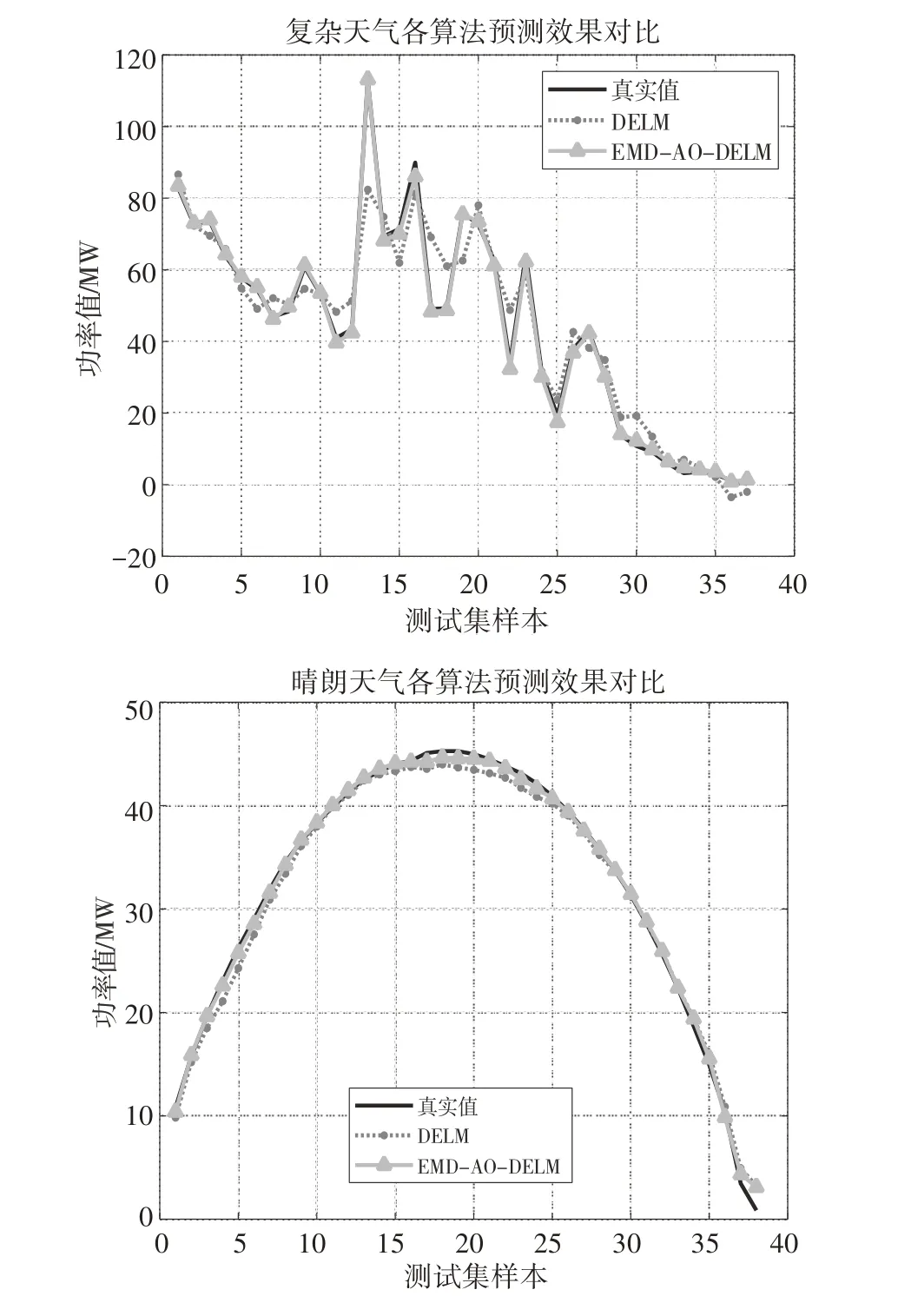
图7 预测仿真结果

综合图7 和表2 来看，晴天预测精度最高，主要是因为日照相对稳定，且光照呈现有规律的正态分布.复杂天气预测精度相对较差是因为日照不稳定且无规律，降水与云量较多，影响到光伏面板接收日照辐射.晴天数据呈现典型的正态分布，符合实际功率情况，预测模型准确无误.

表2 误差指标数据

综上所述，通过仿真图以及表2 误差分析，本文提到的EMD-AO-DELM 模型相较于初始DELM模型，预测精度得到显著提升，模型稳定性更好，各项指标明显优于其余两种算法,能够胜任实际光伏功率预测需求，更好地配合光伏并网调度工作.

4 结论

本文分析了5 月份的光伏发电预测情况，对光伏发电影响因素进行了相关性分析，并对光伏历史发电功率进行了EMD 分解，对每个IMF 分量分别输入AO-DELM 模型，最后将各分量结果进行求和以得到预测结果.进而提出了一种基于EMDAO-DELM 的光伏功率预测模型，通过仿真结果分析，得到如下结论：

（1）在光伏发电影响因素当中，光照总辐射和散射辐射与光伏功率呈现正相关，对最后的预测结果起到关键性作用；气压和湿度与光伏功率呈现负相关，在实际功率预测中，不宜作为输入数据.

（2）针对光伏功率具有波动性和随机性的特点，对历史光伏功率数据进行了EMD 分解，各分量之间相互独立，分别进行预测，最后进行叠加求和.仿真结果表明，采用EMD 分解方法后的预测效果更好.

（3）本文实验方法在晴天以及复杂天气的预测表现均优于DELM 模型.其中，晴天预测精度最高，这与日照辐射呈有规律的正态分布、日照辐射较为稳定有关.