电流迁移态序列特征模型与获取方法研究*
张慧,刘帅,杨泽丞,王萍,程红梅,张振亚†
(1.智能建筑与建筑节能安徽省重点实验室安徽建筑大学,安徽 合肥 230022;2.安徽建筑大学电子与信息工程学院,安徽 合肥 230022;3.安徽建筑大学经济与管理学院,安徽 合肥 230022)
0 引言
电是现代生产、生活不可替代的能源形式,用电过程的管控事关用电安全,一直为行业应用所关注.随着物联网技术的普及,精细的用电监测与管理日益为越来越多的研究者所关注[1-3].目前,对于用户需求侧的用电研究,主要是基于电力负载特征,如电压、电流、功率等,对电器进行稳态分析、暂态分析以及两者混合分析的方式进行[4].文献[5]从电器电流波形中提取了电流峰值、电流均值、电流均方值、高电平比、低电平比等10个时域和稳态特征,采用k-最近邻规则(k-NNR)和支持向量机进行负载识别,并将主成分分析与k-NNR和SVM相结合分别对10个特征进行检验,选择出最有效的特征.文献[6]使用智能插座采集电器用电数据,从负载功率序列样本中提取负载的功率特征和人的行为特征,提出了一种基于贝叶斯分类模型的家用电器识别算法.文献[7]基于V-I轨迹的信息,如面积、斜率、曲率、轨迹质心等构建稳态和暂态特征.文献[8]从用电数据中构建了时间和频谱负载特征,并提出了双流卷积神经网络(TSCNN)从两种类型的负载特征中提取特征并执行分类.相比稳态特征,暂态特征与设备本身的特性相关性更强[9-10],且用电设备之间的暂态特征重叠较少,有利于用电负荷的分解.对于暂态特征的提取,常使用信号分析方法将高频采集的用电数据转换为频域或小波域.短时傅里叶变换(STFT)和快速傅里叶变换(FFT)广泛用于提取电流谐波,有助于区分暂态负载特征[11-12].文献[13]和文献[14]基于小波变换进行特征的提取,可以在频域和时域上表示信号,从而允许访问有关信号的局部信息.文献[15]提出使用S变换来提取设备特征,然后将这些特征输入SVM分类器以识别每个电气设备,也取得了较高的分类准确度.但高采样频率对硬件设备以及计算能力均提出了更高的要求,增加了设备成本和计算成本.电流作为一种常见的用户用电态势数据,其实时变化能够及时地反映用电设备状态的变化,通过对电流迁移状态的研究,有助于了解设备运行状态的切换,为用户提供电力使用和管理方面的指导和决策支持.为了快速、有效地提取用电事件特征,本文提出了一种电流迁移态序列特征模型与获取方法,在使用与设备本身特性相关性更强的迁移态特征的基础上,相比信号分析方法计算量较小,能够以较低的成本满足快速、有效地提取电流迁移态序列特征的需求,保证电器工作模式在线辨识的及时性.
由于电器通过智能插座取电时,不仅可以使用户通过智能插座实现对电器的更多操作,也使得电器用电数据的获取更为及时、有效、简洁.本文在使用自主研发的智能插座高频次采集电器[16-17]用电数据的基础上,提出了一种基于微环境的分布式粒子群优化算法(MPSO)的电流迁移态特征提取方法.该方法在构造电流迁移态序列集的基础上,使用一元回归模型描述电流迁移态序列的特征,并使用MPSO算法对电流迁移态序列的特征进行了求解,快速、有效地实现了对电流迁移态序列特征的提取.本文主要贡献:1)根据电流迁移态的数据变化特性提出了一种电流迁移态序列的定位方法;2)设计了电流迁移态序列的一元回归模型特征;3)提出基于微环境的MPSO算法,优化电流迁移态序列特征.
1 电流迁移态特征提取方法
电器在使用时,其工作状态经常从一种状态变化到另外一种状态.通常,当电器稳定在某一工作状态时,电路上的用电态势数据相对稳定;而当电器的工作状态发生变化时,电路上的用电态势数据相应变化.简单的,称电器稳定工作的状态为稳态,相应的,对处于稳态的电器用电情况进行在线监测所获得的电器用电情况的状态序列称为稳态序列.对时间上邻近的两个稳态,电器的工作状态从前一个稳态迁移到后一个稳态时,一般不能够从一个稳态瞬时进入下一个稳态,而是需要一定的时间间隔,称这段时间间隔内对电器用电情况进行在线监测所获得的电器用电情况的状态序列为迁移态序列,相应的,称这段时间内电器所处的状态为迁移态.电器的工作/使用过程,是其在稳态与迁移态之间不断切换的过程.
电流值是一类基础的电态势数据,基于高频次采集的电流数据迁移态特征提取是用户侧用电研究中经常面对的问题.电流迁移态特征提取流程如图1所示.
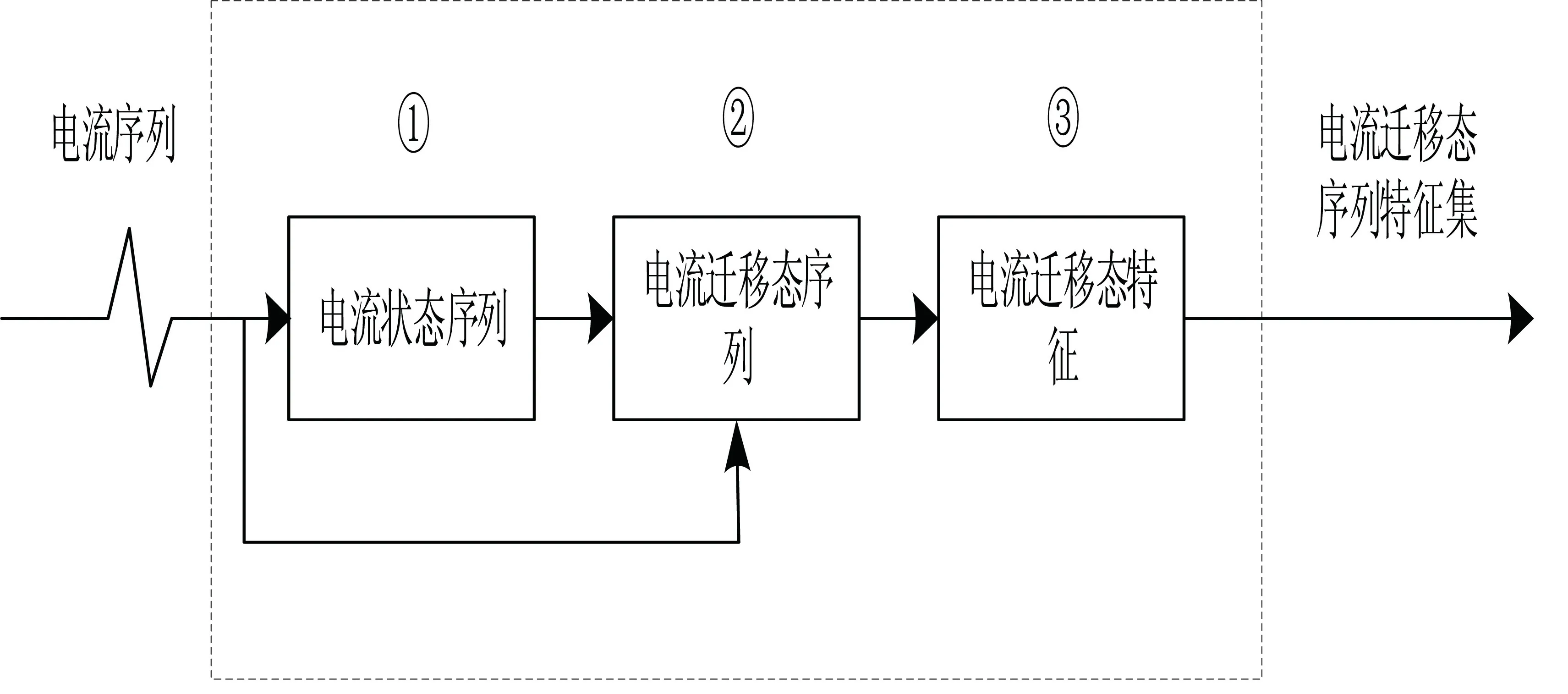
图1 电流迁移态特征提取
图1示意的流程主要包含三个部分:电流状态序列模块①、电流迁移态序列模块②、电流迁移态特征模块③.电流状态序列模块①对电流序列进行深度解析,析构出电流序列中的每一个稳态序列;电流迁移态序列模块②以电流状态序列模块①输出的稳态序列以及电流序列为输入,析构出蕴含于电流序列中的电流迁移态序列;电流迁移态特征模块③负责将电流迁移态序列模块②输出的电流迁移态序列转换为电流迁移态特征.
定义1用电电流序列与电流状态序列ε片段
设t0,tn∈R,t0>0,tn>0,t0<tn,T=(t0,tn]为观测时间段,对t0<t1<···<ti<···<tn,需要在(ti-1,ti]时间段内观测一次电路中的电流.又设si是(ti-1,ti]时间段内观测到的电流值,i=1,2,···,n,称S=<s1,s2,···,sn>为在T=(t0,tn]时间段内的用电电流序列.进一步,设es(ε)l=<sl,sl+1,···,sl+m>,es(ε)l⊆S,是Δml=(tl,tl+m]时间段内的用电电流序列,m是时间段内观测到的电流值个数,若不等式组(1)成立,称esl(ε)是一个电流状态序列ε片段,电器在时间段内电流状态处于ε稳态,esl(ε)是一个电流状态序列ε片段.
不等式组(1)设定的是一种基于均值的电流状态序列ε片段.实践中可以由类似不等式组(2)的其它约束条件规定电流状态序列ε片段,这里,不等式组(2)设定的是一种基于跃变检测的序列ε片段:在一个电流状态序列ε片段中,任意两个相邻观测到的数据,其差异值不大于ε.
定义2电流状态序列片段
对S中全部电流状态序列ε片段构成的电流状态序列ε片段集i1<i2<···<iu,对应的时间片段为τsij.令τsij=(τsij,begin,τsij,end],对τsi与τsi+1,若τsi,end=τsi+1,begin且≤Δ>0,需要将与合并为一个序列片段,称为电流状态序列片段;若不满足,则称es(ε)i与分别为一个电流状态序列片段.
对T时间段内的观测电流序列S=<s1,s2,···,sn>,ε>0,Δ>0,设S中蕴含了k个电流状态序列片段,esi是第i个电流状态序列片段,i=1,···,k,称ES={es1,es2,···,esk}是S中全部电流状态序列片段构成的电流状态序列片段集.
易证,任意两个电流状态序列片段,其对应发生时间段的交集为空.
定义3电流迁移态序列
设S=<s1,s2,···,sn>为T=(0,t]时间段内的观测电流序列,ES={es1,es2,···,esk}为S中全部电流状态序列片段构成的电流状态序列片段集,esi(1≤i≤k)是电流状态序列片段,esi对应的时间片段为τsi=(τsi,begin,τsi,end],τsi,begin≥0,τsi,end≥0,τsi,begin≤τsi,end.称esi为一个电流稳态序列,1≤i≤k,相应的,电器在(τsi,begin,τsi,end]时间段内的运行状态为电流稳态,简称稳态.进一步,令τs0,end=0,τsk+1,begin=t,movei为(τsi-1,end,τsi,begin]对应的电流序列,称movei为一个电流迁移态序列,相应的,电器在(τsi-1,end,τsi,begin]时间段内的工作状态为电流迁移态,简称迁移态.
电流迁移态序列的获取是电流迁移态特征提取的基础,图2给出了电流迁移态序列的生成框架,该框架是图1中的模块①和模块②的细化.图1示意的电流迁移态特征提取流程中,模块①和模块②用于电流迁移态序列的确定.

图2 电流迁移态序列生成框架
图2示意的电流迁移态序列生成框架中:首先,基于类似不等式组(1)的约束条件的电流稳态判别策略ε被用来从样本电流序列中解构出全部的电流状态序列ε片段;接着,全部的电流状态序列ε片段被片段合并策略Δ处理生成全部的电流状态序列片段集作为样本电流序列中全部的电流稳态序列;迁移态生成策略在接收到电流状态序列片段集后,将每个电流状态序列片段从样本电流序列中消除,获得全部的电流迁移态序列.关于一个刚刚获得的电流观测值是否属于当前电流状态序列ε片段的判别策略在算法1中给出.算法1依据不等式组(2)设计:若待判别的电流观测值与当前电流状态序列ε片段最后一个数据差异较大,待辨识的电流观测值不属于当前电流状态序列ε片段.

以算法1为辨识策略,电流序列S中的全部电流状态序列ε片段获取的流程由算法2给出.算法2通过从头到尾逐一对每个电流数据使用辨识策略stableJudge获取S中的每一个电流状态序列ε片段,并保存到全部电流状态序列ε片段集εES中.

图2中,电流状态序列ε片段集由片段合并策略Δ生成,算法3描述了合并策略Δ的流程.getFirstElement()用于获取电流状态序列ε片段集的首个元素,即第一个电流状态序列ε片段;isAdjacent()用于判别两个ε片段集在电流序列S中是否相邻,相邻时返回值为1,否则为0,且最后一个参数为空时,返回值亦为0;mean()返回电流状态序列ε片段的平均值;concat()用于将候选电流状态序列片段的前部和尾部拼接成新的候选电流状态序列片段的前部.

在使用算法3获得全部电流状态序列片段集后,依据定义3,将每个代表电器处于稳定工作状态时的电流状态序列片段从电流序列片段中剔除,即获得电流序列中全部电流迁移态序列片段,实现电流迁移态序列片段集的获取.电流迁移态序列片段集获取算法(生成策略)在算法4中给出.

为高效获得电流迁移态序列片段集,无论是电流状态序列ε片段集还是电流状态序列片段集,其中作为集合元素的每一个片段都按照其首个数据在电流序列集中的位置从前到后渐次存储.需要注意的是,由于用电设备的不稳定性,可能使得迁移态序列较为复杂,实际应用过程中,需要进一步排除不稳定状态对电器工作状态辨识的影响.
电器运行时从一个稳定状态迁移到另外一个稳定状态虽然一般不需要太多的时间,但也存在一定的波动,这意味着一个迁移态序列中数据的个数是变化的.为统一描述每一个迁移态,将每个迁移态序列进行了一元线性回归处理,一元线性回归方程的两个常系数作为该迁移态序列的特征表示.
设S=<s1,s2,···,sn>是一个电流迁移态序列片段,S′=<s′1,s′2,···,>是一元线性回归模型对序列S中每个值的估计,成立:
对每个电流迁移态序列片段,式(3)常系数(a,b)的最优值即是该序列的特征.规定E(S,S′)如式(4),则对电流迁移态序列片段S,其特征(a,b)是式(5)描述最优化问题的最优解,如式(3)中的常系数a和b.
2 基于MPSO算法的特征求解
用电数据采集过程中,出现了约11%的电流数据缺失,针对这种情形,使用粒子群优化算法(Particle Swarm Optimization,PSO)求解电流迁移态序列片段S一元线性回归模型常系数.
PSO算法中,设t时刻某粒子位置在x(t)、速度为v(t),则t+1时刻,其位置x(t+1)与速度v(t+1)一般按照式(6)、式(7)规定的策略更新.式(6)中,ω是惯性因子,c1、c2是学习因子,rand()是随机数,pBest是粒子的历史最优位置,而gBest是全部粒子的历史最优位置.相应的算法流程在算法5中给出.

由于PSO算法是一种基于种群的随机优化算法,所生成的解是最优解的逼近,对具体的最优化问题,一般需要使用PSO算法重复多次执行获得一组最优解的逼近后,从中选取最优的作为问题的最优解,这种方式将显著增加最优化问题求解的时间.
为加速使用PSO算法求解最优化问题,对粒子群优化算法,本文所有的粒子划分成若干个组,一个包含若干个粒子的组被视为一个微环境:1)微环境内,以微环境内的粒子为种群,可以独立执行适应微环境信息特性、类似算法5的PSO算法;2)一个微环境内全部粒子的历史最优位置保存在微环境内;3)一个微环境与若干个微环境可以进行信息交互,互相查询被查询微环境内的历史最优的粒子的位置信息;4)从信息交互的角度看,全部微环境形成了一个以微环境为节点的微环境网络;5)微环境网络中,邻接的微环境节点可以进行信息交互,不相邻的微环境节点不能够进行信息交互.图3示意了一个微环境网络拓扑结构.

图3 微环境网络拓扑结构
图3中,每个灰色圆点表示一个微环境节点,边表示了微环境节点的连接(信息交互)情况.逻辑上,全部微环境节点以5行4列形式排列,共20个微环境节点.每个微环境节点只能够向直接邻接的微环境节点发送查询请求,任意两个不直接连接的微环境节点不能直接交换数据.
相应的,对基于微环境的PSO算法,设:1)每个微环境中有若干个粒子;2)对任意微环境,记gBestL是该微环境中全部粒子的历史最优位置;3)对某个微环境,若其有m个邻居微环境,记gBestLi是其第i个邻居微环境中全部粒子的最优位置,规定gBestA如式(8).则对基于微环境的PSO算法,某个微环境中任意粒子,若t时刻其位置为x(t)、速度为v(t),则其在t+1时刻的速度v(t+1)与位置x(t+1)可以依据式(9)、式(7)确定.称式(8)是基于微环境的PSO算法的数据交换策略,而式(9)、式(7)是基于微环境的PSO算法中粒子位置的更新策略.相应的算法流程在算法6中给出.

算法6中,以粒子的适应度值评估每个粒子位置的优劣:适应度值越小,粒子位置越优越;粒子的适应度值用适应度函数fun计算,该函数以粒子的位置为自变量.
设gBest是k时刻微环境网络中全部微环境全部粒子的全局最优位置,则对微环境网络中任意微环境,成立:fun(gBestL)≥fun(gBestA)≥fun(gBest).因此,类似式(6)、式(7)规定的粒子群优化算法中粒子速度与位置更新,对任意一个微环境中的粒子群中的粒子使用式(9)、式(7)更新速度和位置,该微环境中的粒子群中粒子位置收敛.进一步,对全部微环境中的粒子群,虽然gBest可能不出现在每个微环境的粒子群中,但依据微环境网络中微环境的连接特性和式(8)可知,由于任意两个微环境在微环境网络中有限步可达,故全局最优位置gBest可以经过有限次迭代传递到微环境网络中每个微环境上的粒子群(极端情况:微环境网络中全部m个微环境线性排列,设第一个微环境是A,最后一个微环境是B.若最优位置gBest是A微环境粒子群中的局部最优位置,则至多经过m-1次迭代,B微环境上的局部最优位置优于m-1次迭代前A节点的粒子群的局部最优位置,即优于m-1次迭代前的全局最优位置).显然,式(8)规定的数据交换策略可以使全局最优位置gBest在微环境网络中每个微环境上传播,而全局最优位置gBest可以传递到微环境网络中每个微环境,意味着微环境网络中每个微环境上的粒子群本地局部历史位置gBestL距全局最优位置有限步可达,表现为当算法6运行结束时,每个微环境中粒子群的本地局部历史位置gBestL的适应度值差异较小.
使用PSO算法求解式(3)描述的电流迁移态序列片段S一元线性回归模型常系数a、b时,(a,b)是PSO算法中的一个粒子.使用MPSO算法求解电流迁移态序列片段S一元线性回归模型常系数的流程由算法7给出.

算法5、算法6和算法7使用适应度函数fun计算粒子的适应度值时,其输入为粒子的位置.算法7在计算粒子的适应度值时,还需要将电流迁移态序列片段S作为输入.使用算法7求解电流迁移态序列片段一元线性回归模型常系数的适应度函数依据式(4)设计,详细流程在算法8中给出.

3 实验结果与分析
实验使用的电流数据序列为智能建筑与建筑节能安徽省重点实验室自主研发的智能插座系统采集的微波炉工作时的电流观测数据,每2秒采集一次,共3 193个.使用算法1~算法4获取蕴含于电流数据序列中的电流迁移态序列,当ε=0.01、Δ=0.03时,有184个电流迁移态序列.图4(a)给出了全部3 193个电流数据的序列以及184个电流迁移态序列的形态,图4(b)给出了前250个电流数据组成的电流数据序列片段以及蕴含其中的电流迁移态序列的形态.图4(a)和图4(b)中,电流数据序列使用蓝色线段表示,电流迁移态序列使用红色线段表示.显然,由于每个电流迁移态序列都是电流数据序列的片段,图4(a)和图4(b)中,每个红色线段都覆盖了同样的蓝色线段.同时,从图4(a)和图4(b)可以直观地发现:每个电流迁移态序列对应的都是电流数据序列中上升或者下降比较快的片段.

图4 电流数据序列与迁移态序列
实验分别使用算法5描述的PSO算法、文献[18]提出的混沌自适应粒子群优化算法(CAPSO算法)和算法6描述的基于MPSO算法求解式(3)规定的电流迁移态特征.对PSO算法,设置粒子数为400,学习因子c1、c2为2,惯性因子ω为0.8.对CAPSO算法,设置粒子数为400,惯性权值wmax和wmin分别为0.9和0.4,自适应加速度系数cmax和cmin分别为2.5和0.5,混沌搜索参数ξ为0.2.对MPSO算法,设置网络拓扑结构为图3所示的5行4列网格,共20个微环境节点;对每个微环境,粒子数设置为20(这样,全部微环境中的粒子数总和为400,与PSO算法和CAPSO算法一致),学习因子c1、c2为2,惯性因子ω为0.8.
表1和表2分别给出了重复20次使用PSO算法和CAPSO算法求解全部184个电流迁移态序列特征时,每次求解获得全部184个电流迁移态序列特征性能的最小值、最大值、平均值、中位值、下四分位Q1、上四分位Q3、方差以及使用时间等信息;使用MPSO算法构造全部184个电流迁移态序列特征时,每个微环境内求解出的全部184个电流迁移态序列特征性能的最小值、最大值、平均值、中位值、下四分位Q1、上四分位Q3、方差以及使用时间等信息在表3中给出.其最小值、最大值、平均值、中位值、下四分位Q1、上四分位Q3、方差是全部184个电流迁移态序列特征依据式(4)规定性能的统计值.
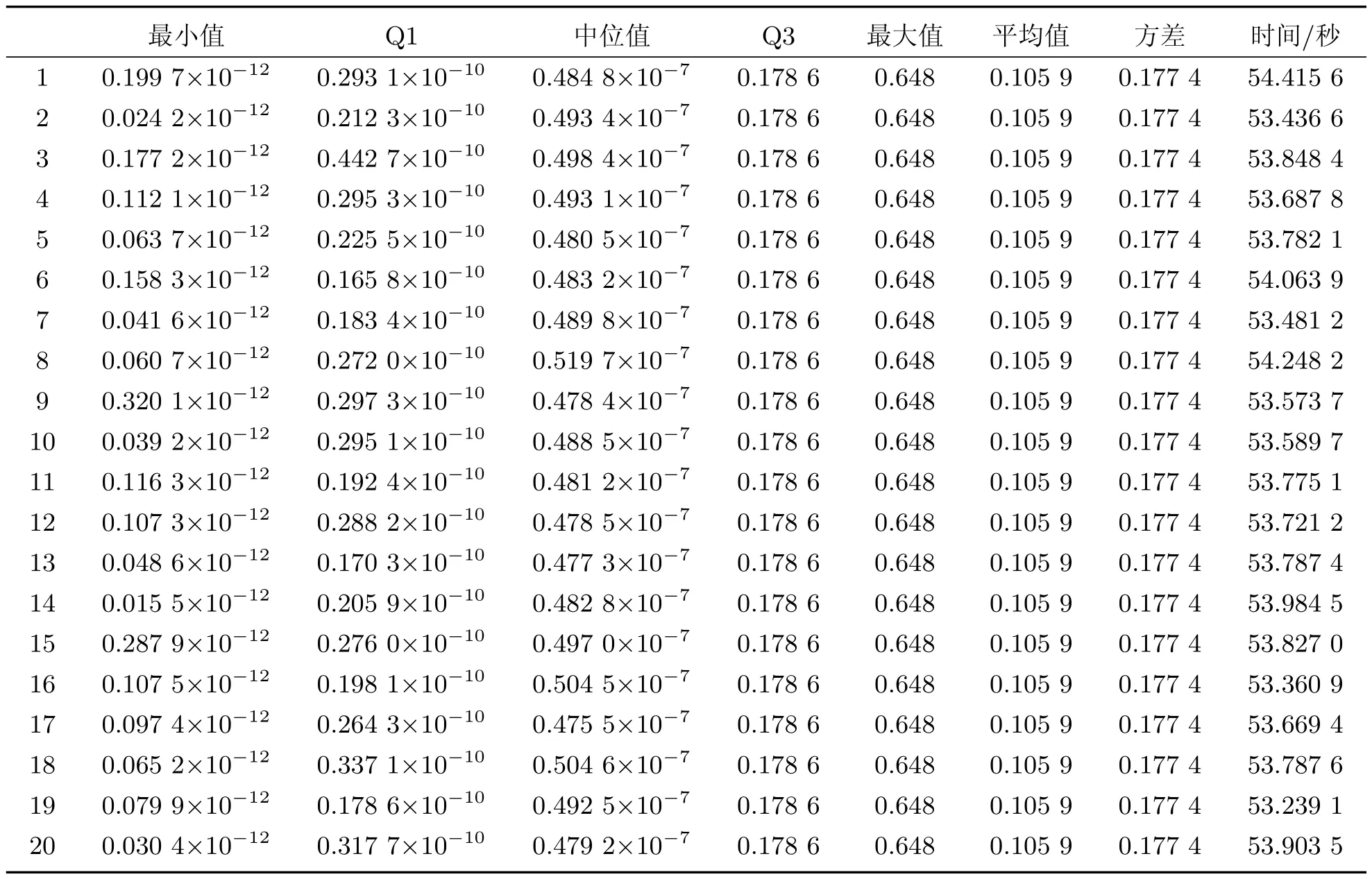
表1 PSO算法的性能(迭代次数:100)

表2 CAPSO算法的性能(迭代次数:100)
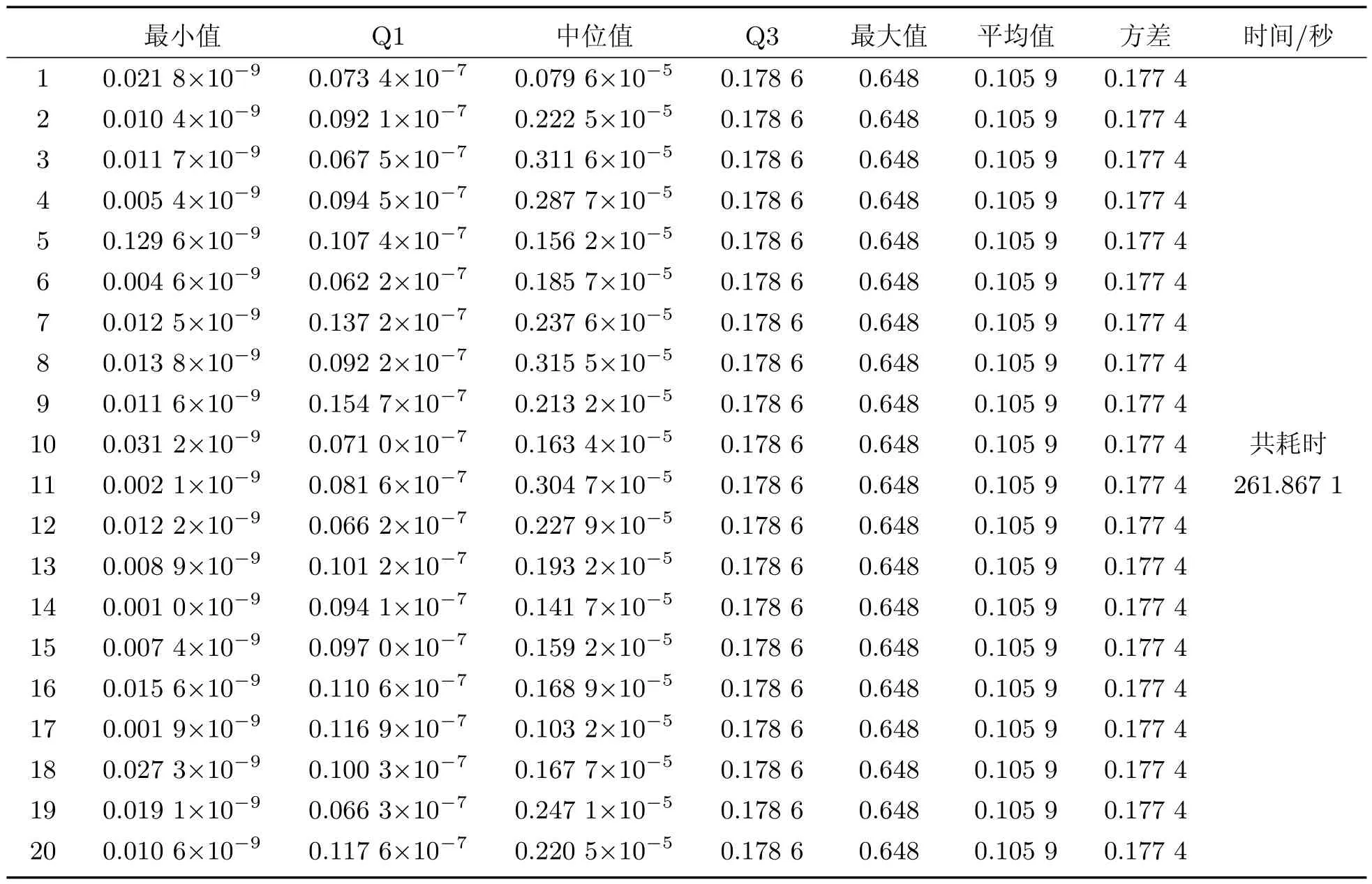
表3 MPSO算法的性能(迭代次数:100)
表1和表2中,时间栏记录的是PSO算法和CAPSO算法求解全部184个电流迁移态序列特征使用的时间,而表3中时间栏记录的为MPSO算法运行一次的时间.文献[19]对分布式平台的通信开销进行研究,发现基于局域网的分布式平台任意两个节点间的平均延迟不大于0.27毫秒,网络性能可满足对通信时间的要求.
对比表1、表2和表3中最小值、最大值、平均值、中位值、Q1、Q3、方差等数据,可以断言,无论是PSO算法、CAPSO算法还是MPSO算法都可以用于电流迁移态序列特征的有效求解.考虑到PSO算法和CAPSO算法求解最优化问题时一次执行获得的最优解只是近似最优解,为获得更接近最优解的近似最优解,一般需要重复多次执行算法,这使得PSO算法和CAPSO算法求解最优化问题时需要更多的时间.使用MPSO算法求解最优化问题时,算法的1次执行可同时获得与微环境个数相同数量的近似最优解,效率上要比使用PSO算法高许多.由表1和表2中时间数据可知,每次PSO算法求解全部184个电流迁移态序列的特征使用时间的最小值为53.239 1秒、最大值为54.415 6秒,平均值为53.759 2秒,方差为0.284 5秒,全部20次求解共耗时1 075.183 1秒;每次CAPSO算法求解全部184个电流迁移态序列特征使用时间的最小值为69.391 1秒、最大值为70.796 0秒,平均值为70.114 1秒,方差为0.440 7秒,全部20次求解共耗时1 402.281 8秒;而表3中时间数据显示,MPSO算法一次运行即可获得20组近似最优解,共耗时261.867 1秒,平均每个近似最优解的求解耗时13.093 4秒,远小于一次用PSO算法和CAPSO算法求解全部184个电流迁移态序列特征平均需要的时间,MPSO算法用时仅是PSO算法和CAPSO算法的24.355 6%和18.674 4%.
图5、图6分别给出了使用PSO算法和CAPSO算法一次求解全部184个电流迁移态序列特征时性能的最小值、最大值、平均值、中位值、Q1以及Q3随着迭代次数增加的变化情况.显然,随着迭代次数的增加,性能的最小值、最大值、平均值、中位值、Q1以及Q3快速下降后渐趋稳定.图7给出了使用MPSO算法求解全部184个电流迁移态序列特征时一个微环境内性能的最小值、最大值、平均值、中位值、Q1以及Q3随着迭代次数增加的变化情况.显然,与使用PSO算法一次求解全部184个电流迁移态序列特征时性能的变化一样,随着迭代次数的增加,MPSO算法性能的最小值、最大值、平均值、中位值、Q1以及Q3快速下降后渐趋稳定.对照图5、图6、图7,CAPSO算法在迭代50次后,性能的最小值、最大值、平均值、中位值、Q1以及Q3都渐趋稳定;而PSO算法和MPSO算法在迭代20次后,性能的最小值、最大值、平均值、中位值、Q1以及Q3就渐趋稳定.
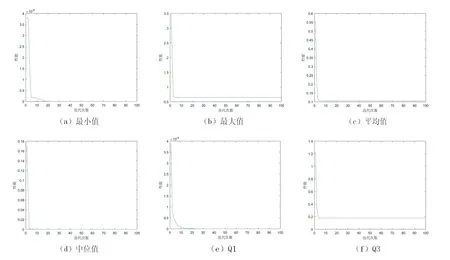
图5 PSO算法的性能(迭代次数:100)
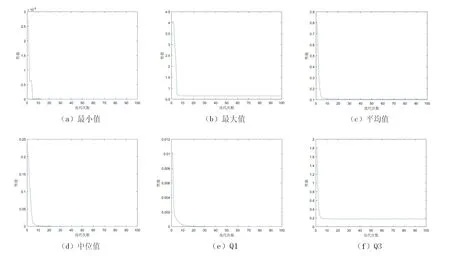
图7 MPSO算法的性能(迭代次数:100)
图8给出了迭代次数为20时,使用PSO算法一次求解全部184个电流迁移态序列特征性能的最小值、最大值、平均值、中位值、Q1以及Q3随着迭代次数增加的变化情况.显然,随着迭代次数的增加,性能的最小值、最大值、平均值、中位值、Q1以及Q3快速下降,在接近迭代后渐趋稳定,这意味着使用PSO算法求解电流迁移态序列特征时,迭代次数设置为20是合适的.重复20次使用PSO算法求解全部184个电流迁移态序列特征,使用时间的分布直方图如图9所示.PSO算法使用时间的最小值为11.265 1秒、最大值为11.821 6秒,平均值为11.405 6秒,方差为0.148 7秒,显然,使用PSO算法求解电流迁移态序列特征是稳定的.

图8 PSO算法的性能(迭代次数:20)

图9 PSO算法用时分布直方图(迭代次数:20)
图10给出了迭代次数为20时,使用MPSO算法求解全部184个电流迁移态序列特征时,一个微环境中算法性能的最小值、最大值、平均值、中位值、Q1以及Q3随着迭代次数增加的变化情况.显然,随着迭代次数的增加,性能的最小值、最大值、平均值、中位值、Q1以及Q3快速下降,在接近迭代后渐趋稳定,这意味着使用MPSO算法求解电流迁移态序列特征时,迭代次数设置为20是合适的.实验中,迭代次数设置为20时,20个微种群完成184个电流迁移态序列特征的求解用时56.323 9秒,每个微环境平均用时2.816 2秒,是使用PSO算法用时的24.691 4%,这再次印证了使用MPSO算法可以快速地完成电流迁移态序列特征的求解.

图10 MPSO算法的性能(迭代次数:20)
使用BP神经网络对提取出的电流迁移态特征进行电器状态的辨识,重复进行实验100次,图11给出了100次实验电器状态辨识准确率(Accuracy)的分布情况:最大值为1,最小值为0.781 8,平均值为0.979 3,中位值为0.981 8.可知使用本文所提电流迁移态序列特征模型提取出的特征能够以较高的稳定性和准确率实现对电器状态的辨识.
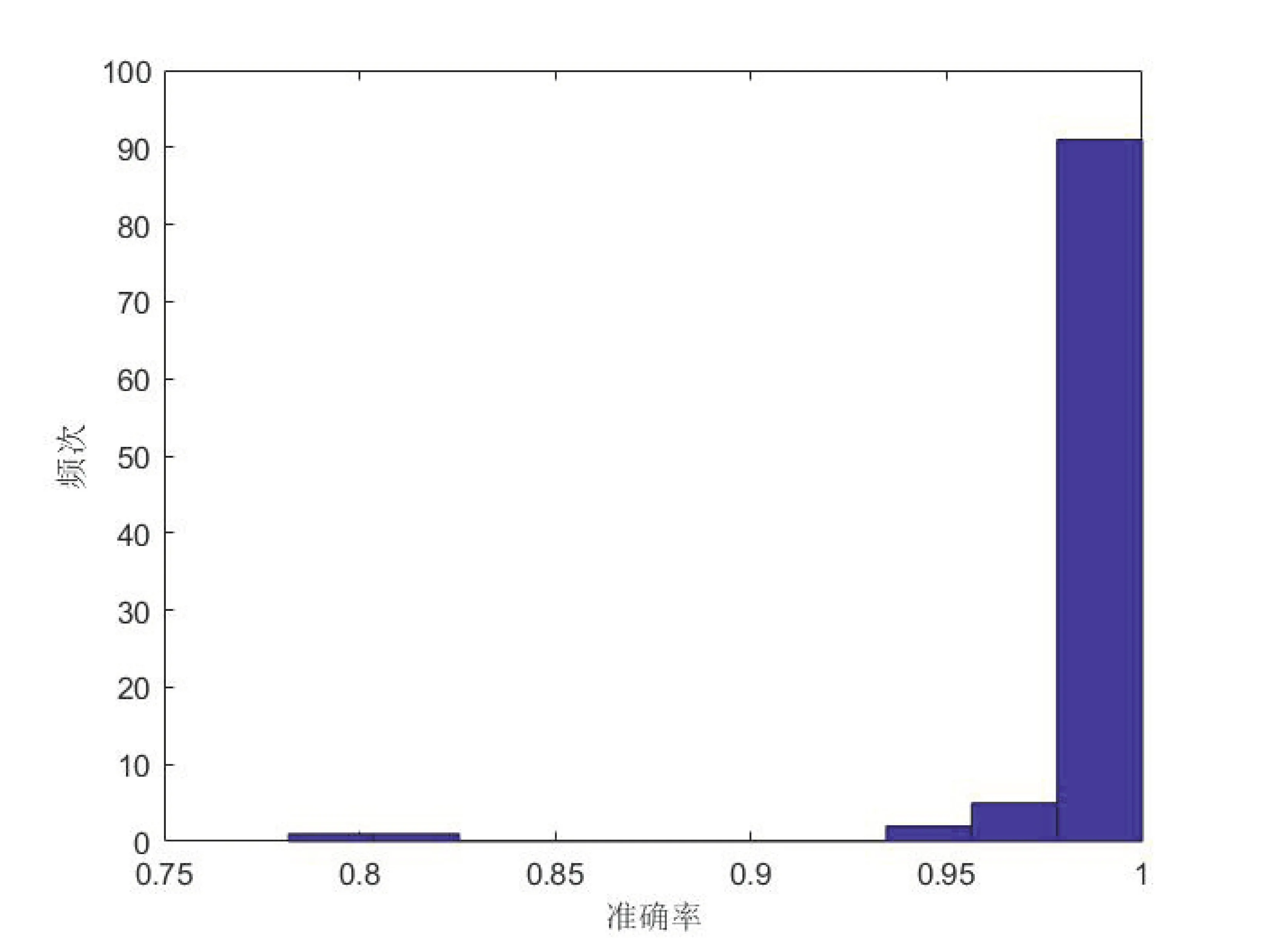
图11 电器状态辨识准确率分布直方图
实验使用曙光W760-g20服务器完成,该服务器的CPU为2个Intel(R) Xeon(R) CPU E5-2637 v3,192 GB ECC内存,操作系统为Windows 10,Matlab使用R2017a版本.
4 结论与展望
物联网技术的进步与普及丰富了用户用电态势在线监测的手段,促进了需求侧用电过程的监测与管理.特别是针对诸如安全用电、智慧园区、智慧社区、智慧建筑等场景的应用需求,其中电器及其工作模式的在线辨识为越来越多的研究者所关注.为快速辨识电器的工作状态,本文使用一元回归模型描述电流迁移态序列的特征,通过电器工作状态切换的辨识进行电器工作模式的在线辨识.电流迁移态序列的一元回归特征计算量小的优势,保证了电器工作模式在线辨识的及时性.同时,为提升电器工作模式在线辨识的准确性,面向电流迁移态序列特征的优化,本文还提出了基于微环境的粒子群优化算法(MPSO算法).与使用PSO算法和CAPSO算法优化电流迁移态序列特征相比,MPSO算法通过多个微环境的协作,使用相比PSO算法和CAPSO算法更少的粒子数进行计算,在取得与PSO算法和CAPSO算法一致性能的同时,执行速度显著提升.
微环境网络是MPSO算法的计算架构,本文使用了只有邻居微环境才能够交换信息的5×4网格实现了MPSO算法,并高效地优化了电流迁移态序列的一元回归特征.网络拓扑对MPSO算法性能的影响值得进一步研究.
本文所提MPSO算法本质上是该算法在Matlab环境中的串行实现.诸如边缘计算、群智能建筑平台等真实的分布式信息处理环境中,MPSO算法计算过程的优化以及网络通信开销,对算法性能的影响是需要关注的.进一步,不同微环境信息处理的同步与异步对算法性能的影响、深度算力以及异构算力下的MPSO算法及其应用都是值得深入开展的工作.

