基于改进的径向基神经网络模型的水库异重流泥沙淤积量模拟

韩 睿

(辽宁省铁岭水文局，辽宁 铁岭 112000)

水库库容调节受水库异重流泥沙淤积影响较为明显，水库异重流泥沙淤积量预测精度影响因素较多，使得其一直是水库泥沙淤积的难点问题[1]。水库异重流泥沙淤积量呈现明显的非线性变化特征，传统线性预测模型很难对其进行相对准确的预测[2]。当前，国内对于水库异重流泥沙淤积量预测主要采用径向基神经网络模型，该方法可通过降到水库异重流泥沙预测变化的差异性，通过标准化处理降低水库泥沙淤积数据系列变化的不稳定性，从而可提高其预测的精度，在国内一些大型水库异重流泥沙淤积中得到不同程度的影响[3-8]，但传统径向基神经网络模型由于对变量设置较为主观，使得其模型收敛速率较慢，往往很难取得有效求解[9]。针对传统径向基神经网络模型收敛速率慢的问题，有学者通过引入梯度优化函数对其进行变量进行优化计算，通过实例应用[10-15]，明显可提高传统径向基神经网络模型收敛速率，从而提升其在非线性变化数据系列中预测的精度，但改进模型在大型水库异重流泥沙淤积量预测中还未得到具体应用，为此本文引入改进的径向基神经网络模型，以铁岭地区石佛寺水库为具体实例，对该水库异重流泥沙淤积量进行预测，并结合测定的泥沙淤积量进行模型检验。研究成果对于水库泥沙淤积的趋势预测方法具有参考价值。

1 改进模型原理

改进的径向基神经网络模型通过对多个变量节点进行映射方程的计算来构建其计算序列样本：

(1)

式中，X=[x1，x2，…xH]T—模型计算变量组合序列；YP—模型求解目标函数值；Wj—模型变量求解权重值；D(XP，tj)—模型变量核函数；tj=[tj1，tj2，…tjm]为核函数计算目标值。

改进模型采用高斯函数来构建变量的核函数，计算方程为：

(2)

式中，σj—模型计算误差。

结合目标函数对各变量计算误差进行评估：

(3)

(4)

式中，W0—最小权重变量；O(I1)—变量数据系列矩阵；f—输出变量序列矩阵。

变量序列矩阵计算方程为：

(5)

改进模型在寻求最优求解的过程中采用梯度下降方法对其优化计算：

Δσ=(δMSE2-δMSE1)/α

(6)

[σ0]2=[σ0]1-ηΔσ

(7)

式中，η—训练样本计算次数；[σ0]1和[σ0]2—模型调整后优化计算值。

在模型优化后对其求解精度进行综合评估：

ρ=cov(β，P)/(σβσP)

(8)

式中，cov(βP)—模型协方差；σβ和σp—模型核函数方差计算值。

2 水库异重流泥沙淤积预测

2.1 石佛寺水库概况

石佛寺水库为辽河干流唯一控制型水利工程，坐落于沈阳市法库县，水库总库容为1.85亿m3。水库建库以来，由于上游来水来沙量较大，使得水库多年淤积量较高，结合石佛寺水库建库以来至2020年水库泥沙淤积测定数据，整个泥沙淤积序列资料15年，分别应用改进前后的径向基神经网络模型对水泥异重流泥沙淤积量进行预测，结合水库实际测量的泥沙淤积资料对其预测的精度进行对比分析。

2.2 模型参数检验

分别采用T检验和F检验方法对改进的径向基神经网络模型训练样本数据序列进行参数检验，检验结果见表1—2。

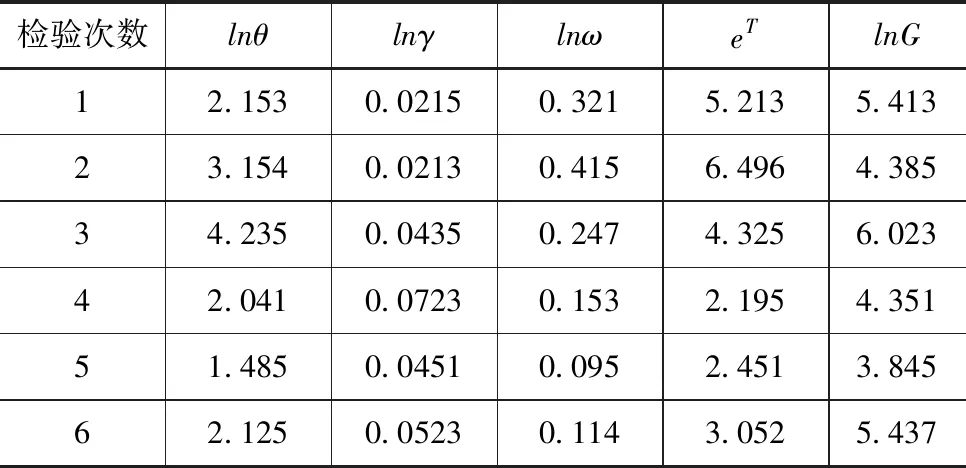
表2 T检验方法模型参数检验结果

从F检验方法模型参数检验结果可看出，在0.05假设检验水平下改进模型各类检验值均高于1.5，模型参数在0.05假设检验水平具有显著性。水库异重流泥沙淤积模拟在改进的径向基神经网络模型下其参数具有相同的误差分布，从T检验方法模型参数检验结果可看出，改进的径向基神经网络模型在T检验方法下其模型参数分布差异性较大，表明相比于传统径向基神经网络模型，改进模型的参数非线性变化具有显著性，适合于水库异重流泥沙淤积量的非线性模拟。

2.3 改进模型收敛率对比

从计算方差、协方差、计算时间、收敛率对改进前后模型在样本数据下的收敛率进行综合对比，综合对比结果见表3。

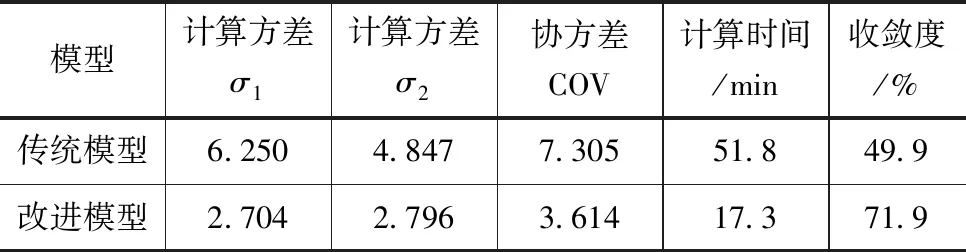
表3 改进前后模型下收敛率综合对比结果

从改进前后模型下收敛率综合对比结果可看出，计算方差和协方差指标在改进模型下相比于传统模型均有所减小，相比于传统模型，改进模型优化求解值相关度增加，从计算时间和收敛度对比结果可看出，相比于传统模型，改进模型计算时间缩短34.5min，收敛度提高22%，相比于传统模型，在相同样本数据系列下，改进模型的综合收敛度得到明显改善。

2.4 改进模型年尺度预测精度对比

结合石佛寺2011—2020年泥沙淤积测定数据，利用石佛寺水库库容曲线变化对其历史泥沙年淤积量进行估算，作为改进前后模型的训练样本数据系列，对改进前后径向基神经网络模型对石佛寺水库年尺度异重流泥沙淤积量进行模拟精度的对比，年尺度对比结果见表4，并对模拟值和实测值的相关性进行分析，相关性分析结果如图1所示。

图1 改进前后年尺度下模拟值和计算值相关性分析结果

图2 改进前后汛期尺度下模拟值和计算值相关性分析结果

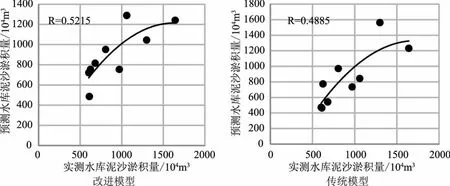
图3 改进前后非汛期尺度下模拟值和计算值相关性分析结果

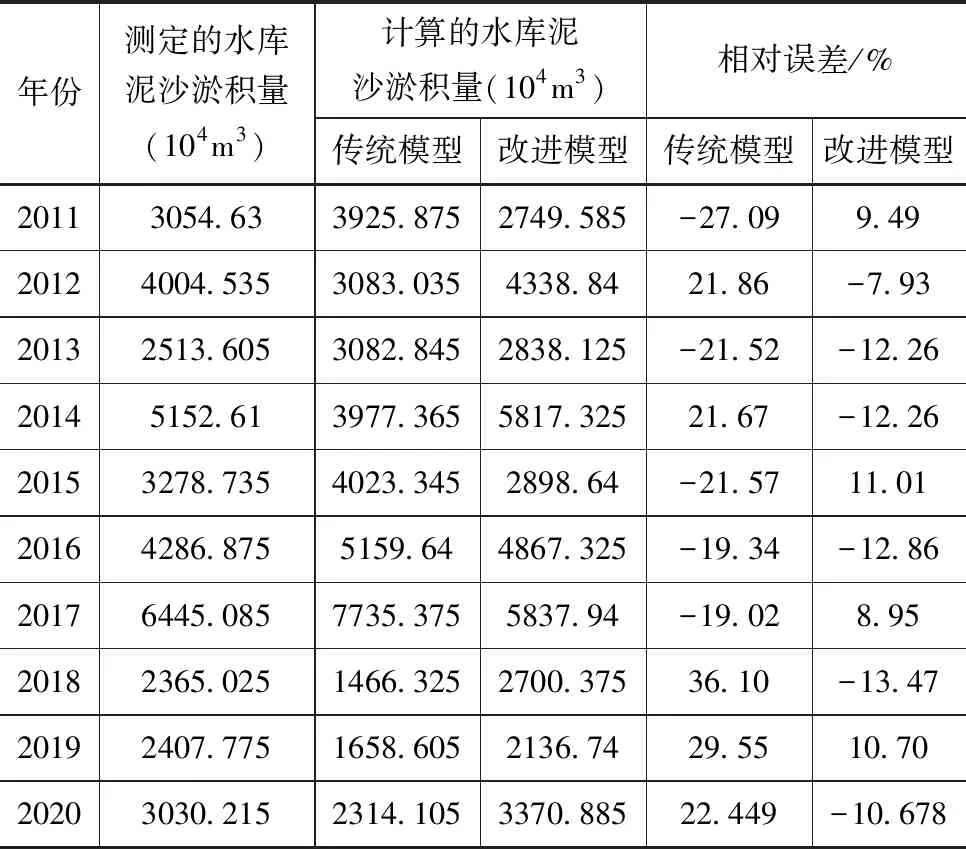
表4 石佛寺水库年尺度异重流泥沙淤积量模拟精度对比

从石佛寺水库年尺度异重流泥沙淤积量模拟精度对比结果可看出，采用改进的径向基神经网络模型由于采用梯度下降方法对其模型变量权重进行优化计算，提高了模型变量权重设置的客观性，相比于传统模型，其收敛度和目标优化求解精度均得到明显改善。相比于改进前，改进后模型各年份泥沙异重流淤积量相对误差平均降低13.1%。从改进前后年尺度下模拟值和计算值相关性分析结果，整个过程下改进模型下石佛寺水库异重流泥沙淤积量模拟值和实测值的相关性均高于0.7，而传统模型下其相关值均低于0.5，改进模型相比于传统模型其相关系数提高约0.2。

2.5 季节尺度水库异重流泥沙淤积模拟精度对比

考虑到石佛寺水库异重流泥沙淤积季节差异性较大，在年尺度泥沙淤积量预测对比分析的基础上，对汛期和非汛期石佛寺水库异重流泥沙淤积预测精度进行对比，分析结果见表5—6。

表5 汛期石佛寺水库传统模型和改进模型下泥沙淤积量预测精度对比

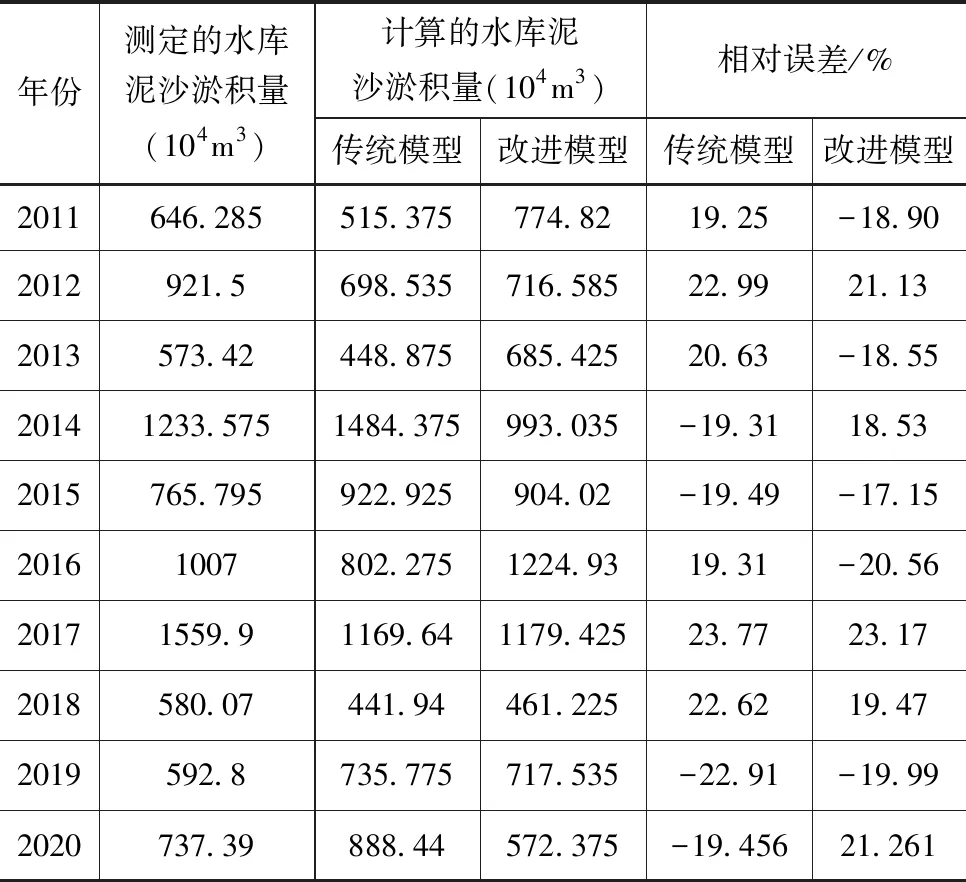
表6 非汛期石佛寺水库传统模型和改进模型下泥沙淤积量预测精度对比

从汛期和非汛期石佛寺水库传统模型和改进模型下泥沙淤积量预测精度对比可看出，两个时间尺度下石佛寺水库异重流泥沙淤积量预测精度相比于改进前都有较为明显的改善，其中汛期尺度下泥沙淤积量预测相对误差相比于改进前平均降低11.2%，非汛期尺度下相对误差均值平均降低1.10%。非汛期尺度下改进前后模型石佛寺水库异重流泥沙淤积预测精度差异性较小，这主要是因为在非汛期水库来水量较少，使得水库异重流泥沙淤积量呈现较为明显的非线性变化，从而降低了改进前后径向基神经网络模型对石佛寺水库泥沙预测的精度。从改进前后汛期和非汛期尺度下水库异重流泥沙淤积模拟值和计算值相关性分析结果可看出，相比于改进前模型，改进后模型水库异重流泥沙淤积预测值和测定值之间的相关系数提高0.2344，而进入非汛期其相关系数有所降低，相比于改进前，其相关系数增加0.033。

3 结语

(1)在采用改进后的径向基神经网络模型对水库泥沙异重流泥沙进行预测中，其样本训练次数对于其目标求解精度影响较大，通过数据试验分析，其样本训练次数建议选为2000次，可进一步模型收敛度。

(2)改进的径向基神经网络模型在T检验方法下其模型参数分布差异性较大，相比于传统径向基神经网络模型，改进模型具有显著的参数非线性变化，适合于非线性变量的预测。

(3)本文分析的石佛寺水库泥沙淤积量相对较小，对于水库异重流泥沙淤积量较大的适用性还需要进一步探讨。