基于自适应横程走廊的再入滑翔飞行器改进预测校正算法
贺杨超, 李 炯, 邵 雷,*, 周池军, 雷虎民
(1. 空军工程大学研究生院, 陕西 西安 710051; 2. 空军工程大学防空反导学院, 陕西 西安 710051)
0 引 言
再入滑翔飞行器(reentry gliding vehicle, RGV)在临近空间的超声速飞行[1],受到气动热、动压和过载等约束[2],大气模型参数的不确定性和气动力的扰动对飞行器的飞行也会造成制约,因而飞行器的再入制导方式成为了各国航空航天领域研究的重点和难点问题[3-4]。通常条件下,RGV的制导方式主要分为标称弹道制导[5-7]和预测校正制导[8-9]两种。
其中标称弹道制导通常利用飞行器实际飞行轨迹参数和弹载计算机预先装订参数的偏差,基于预先设计的制导方法,获得相应的制导律,且经过寻优后,可以在满足约束的条件下达到较高的制导精度,但是该类方法轨迹求解实时性差,且因依赖于参考轨迹,对突发情况的适应性低。与标称弹道制导不同,预测校正制导方法通过不断对飞行终点进行预测,调整控制量来消除预测航程差,实现飞行器的再入制导。凭借更高的制导精度和更强的飞行环境适应性,预测校正方法在RGV的制导律设计中得到了越来越多的应用[10-12]。根据预测校正算法的机理不同,预测校正算法可以分为解析预测校正和数值预测校正两大类。其中,解析预测-校正方法通过设置具有解析形式的方程[13-15],表示再入飞行器的制导过程,得到制导周期内运动方程的近似解,但是该方法要求提前设计特定的解析形式,对飞行环境适应性差,且容易收到参数扰动的影响。
随着现代计算能力的增强,数值预测校正算法在RGV的制导中得到了更多的应用[16-17]。该算法通过设定横纵向的制导逻辑和不断迭代飞行器的运动方程组,得到预测航程,利用预测航程与剩余航程差来修正控制参数,并配合相应的横向制导逻辑实现制导。从流程上而言,数值预测校正算法分为纵向制导与横向制导两个阶段。其中纵向制导阶段需要确定攻角剖面与倾侧角幅值。通常条件下,为更好满足各类约束,攻角剖面会提前设定,将倾侧角作为主要控制量[18]。通过将各类约束转化至倾侧角走廊[19],保证倾侧角幅值始终在走廊内,实现过程约束。利用相邻两次预测航程的差值,使用割线法得到倾侧角幅值[20-21]。横向制导通常会采用航迹偏差角走廊[22]或者横程走廊[23],其中横程因其与剩余航程近似成线性关系,在侧向制导中,往往会达到更高的制导精度和更好的制导效果。其中,Shen等[24]给出了横程参数的定义,提出了一种根据飞行状态实时确定倾侧角反转位置的侧向制导律;李惠峰等[25]用横程和横程微分项相加作为反转控制量,约束横程变化始终在走廊边界内;张科等[26]通过分析横程和剩余航程之间的关系,提出一种边界约束动态变化的横程走廊,提高了飞行器的横向制导精度。而飞行器在横向制导的过程中,通常还会存在不可经过的禁飞区,因此需要设置合理的禁飞区规避逻辑。其中,Zhu等[27]通过利用视距角描述了飞行器飞行路径与禁飞区的相对位置关系,提出每个禁飞区的边界选择算法,实现了最小能量避让;Liang等[28]在侧向制导中考虑禁飞区的航向限制,设置了动态航向走廊,针对禁飞区位置相近的情况,设置了包含飞行轨迹位置和方向约束的航路点进行制导;赵江等[29]通过根据飞行器对禁飞区航向角的导向区域,设置规避逻辑,实现对禁飞区的规避制导。以上方法,均针对禁飞区设计了相应的规避逻辑,但是与横向的制导逻辑存在一定分离,需要通过判断条件,进行逻辑转换,可能会导致飞行器制导失败或者飞行器倾侧角反复偏转。
针对数值预测校正算法的侧向制导中规避逻辑与制导逻辑相分离的问题,本文将飞行器瞬时转弯半径构成的侧向运动轨迹圆与禁飞区是否相交,作为横向制导加入规避逻辑的判断条件;根据禁飞区对飞行轨迹的影响、与飞行器和预定目标点的相对位置关系,提出禁飞区有效映射横程;通过设计自适应横程走廊,将规避逻辑和横向制导逻辑进行融合,使飞行器倾侧角在自适应横程走廊边界的约束下,通过较少次数的翻转,实现对禁飞区的规避和横向有效制导。
1 飞行器模型及约束
不考虑地球自转情况下,RGV无量纲化运动模型如下所示:
(1)

(2)
(3)
飞行器飞行存在过程约束、禁飞区约束和终端约束。其中终端约束表示为
(4)
式中:rf,Vf,φf,φf表示给定的飞行器终端高度、终端速度及终端的经纬度。
过程约束考虑飞行器的热流密度约束、动压约束和过载约束。
(5)

本文将禁飞区设定为一种无限高的圆柱体,飞行器不得从禁飞区中穿过。其函数表达式为
(6)
式中:φb,φb表示禁飞区的中心经纬度;rb表示禁飞区的经纬度半径。
2 预测校正算法
在RGV再入飞行的一个制导周期内,本文用到的预测校正算法的制导过程为:纵向制导通过攻角剖面确定控制变量攻角的值,然后利用割线法求解RGV当前位置到预定目标点的预测剩余航程和实际剩余航程的差值为0时的倾侧角幅值;侧向制导根据是否存在影响飞行轨迹的禁飞区,选择不同的横程走廊约束,控制倾侧角的符号翻转,之后根据RGV当前飞行状态和再入运动方程组式(1)仿真计算本制导周期内的再入轨迹。预测校正算法的制导过程如图1所示。

图1 RGV预测校正算法制导逻辑图Fig.1 RGV predictor-corrector algorithm guidance logic diagram
2.1 纵向制导律设计
2.1.1 攻角设置
为满足飞行器的热防护要求,参考文献[30]中航天飞机式的纵向攻角剖面进行设计,分段函数具体形式如下:
(7)
式中:α表示飞行器的攻角,αmax表示飞行中的最大攻角,αK表示最大升阻比攻角。
本文中给定V1=5 000 m/s,V2=3 000 m/s。
2.1.2 倾侧角走廊
在过程约束下,建立高度-速度(H-V)走廊,如图2所示。首先,将热流密度约束、动压约束及过载约束转化至H-V平面:
(8)
(9)
(10)

(11)

图2 H-V走廊Fig.2 H-V corridor
同时,利用平衡滑翔条件计算航迹倾侧角走廊下边界|σ|cmin如下:
(12)
根据式(11)、式(12),即可建立满足过程约束的倾侧角走廊,|σ|cmin≤|σ|≤|σ|cmax。
2.1.3 倾侧角大小计算
本文使用常值倾侧角剖面,倾侧角幅值通过飞行器的预测航程与剩余航程差f求得
f=Sp(ef)-Stogo_f
(13)
通常条件下的预测校正制导方法使用迭代积分方式获取预测剩余航程,其计算式为
(14)
利用割线法计算σ0,使得f(σ0)=0,具体迭代过程如下:
(15)
式中:ai表示割线法第i次迭代的调节系数;fi表示第i次迭代航程预测差值。
2.2 侧向制导律设计
侧向制导主要是设计一个漏斗式的偏差走廊,常见的有横程走廊和航迹偏角走廊。横程走廊相比较航迹偏角走廊,倾侧角的反转次数更少,具备更好的侧向制导效果。而常见的横程走廊设计中,禁飞区的规避逻辑与横程走廊逻辑是分开设计的,无法保证规避禁飞区后的飞行器横程收敛,即侧向制导很可能会失败,导致飞行器无法到达预定目标点。针对这个问题,本文根据RGV瞬时转弯半径的大小与其瞬时侧向运动轨迹圆的圆心到禁飞区之间的距离进行比较,判断RGV是否需要进行规避禁飞区;当RGV不需要规避禁飞区时,基础横程走廊约束RGV横程,控制倾侧角符号翻转;当RGV需要规避禁飞区时,利用禁飞区有效映射横程,动态调整基础横程走廊边界,控制飞行器的倾侧角翻转,实现禁飞区规避逻辑和侧向制导逻辑的融合,保证在规避禁飞区的同时,飞行器的横程最终依然收敛。
2.2.1 RGV横程走廊
通常条件下,飞行器横程表示为飞行器与目标位置在飞行器速度方向上的投影,其表达式如下:

(16)
飞行器与目标位置剩余航程及视线角定义如下:
Stogo_f=arccos[cosφfcosφcos(φf-φ)+sinφfsinφ]
(17)

(18)
飞行器的航迹偏差角为

(19)
本文设计的基础横程走廊为
(20)
(21)
式中:Stogo_f0为RGV与目标位置的初始剩余航程。在制导过程中,随着Stogo_f逐步接近Stogo_f0,横程走廊也趋近于收敛。
2.2.2 飞行器瞬时转弯半径
通过分析,飞行器气动力的水平分量提供飞行器转弯时的向心力,即
(22)

(23)
为与上述无量纲化运动模型保持一致,无量纲化后的瞬时转弯半径为
(24)
2.2.3 禁飞区有效映射横程

(25)
飞行器的侧向运动轨迹若与禁飞区相交,根据相交情况和几何关系,可以推导出其最先与禁飞区相交的位置的坐标,推导过程如下。
当瞬时侧向运动轨迹圆与禁飞区相交情况如图3所示时,禁飞区和飞行器瞬时侧向运动轨迹圆的圆心距为
(26)
禁飞区圆心到相交弦的距离为
(27)
两个圆心之间连线与纵轴的夹角为
(28)
飞行交点与两个圆心之间连线的夹角为
(29)
即所求交点的坐标公式为
(30)
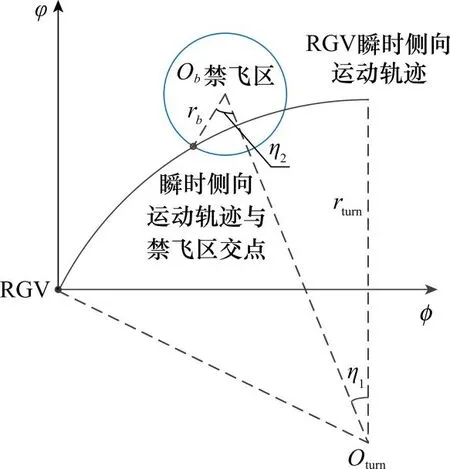
图3 飞行器瞬时侧向运动轨迹示意图1Fig.3 Schematic diagram 1 of transient lateral motion trajectory of aircraft
当飞行器侧向运动轨迹与禁飞区相交情况如图4所示时,交点坐标推导过程中不同的公式如下所示:
(31)
(32)
(33)
飞行器当前位置与禁飞区交点和禁飞区两边界对应的航迹偏角为
(34)
(35)
(36)
式中:
Sb=arccos(cosφcosφbcos(φ-φb)+sinφsinφb)
Spoint=arccos(cosφcosφpointcos(φ-φpoint)+sinφsinφpoint)

(37)

(38)
(39)
(40)
(41)
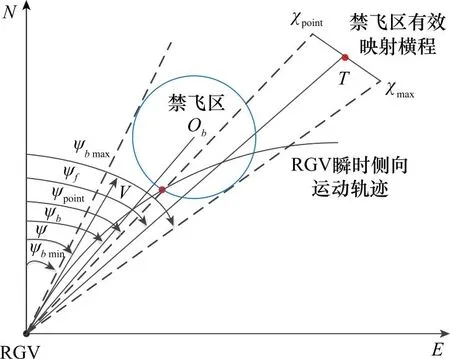
图5 禁飞区有效映射横程示意图Fig.5 Schematic diagram of effective mapping cross range of no-fly zone

2.2.4 自适应横程走廊
在RGV与禁飞区的位置关系满足式(42)时,侧向制导采用自适应横程走廊,否则采用基础横程走廊。
(42)
式中:下标i表示第几个影响RGV飞行轨迹的禁飞区。
侧向制导采用自适应横程走廊时,将禁飞区有效映射横程和基础横程走廊的值进行叠加,得到自适应横程走廊理论值。当横程走廊收敛时,横程便收敛[31],RGV可以飞到预定目标点。即自适应横程走廊的变化率要小于等于飞行器横程的变化率[26],保证RGV横程始终在自适应横程走廊内部。

(43)
(44)
t时刻的自适应横程走廊值为χt max,χt min,表示为

(45)

(46)
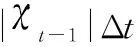
倾侧角的翻转逻辑如下
(47)
3 仿真结果
3.1 仿真条件与对象
仿真计算以CAV-H为对象,其质量为m=987 kg,受力面积为S=0.489 7 m2,升、阻力系数参照文献[32]。制导周期步长形式,制导间隔为0.1 s。运行环境为CPUi5,内存16 G。
3.2 仿真结果分析
(1) 算法有效性分析

算例1制导结果如图6所示,可以看出在无禁飞区约束时,飞行器的横程走廊边界上下对称,变化平缓,横程始终处于走廊中,控制倾侧角在相应时刻进行翻转,有效实现了制导。

图6 算例1仿真结果图Fig.6 Simulation results diagram of Example 1
算例2、算例3的二维制导结果如图7~图10所示,从图7中可以看出,算例2和算例3通过本文的自适应横程走廊,飞行器可以实现对禁飞区的有效规避。其倾侧角变化结果如图8所示,禁飞区有效映射横程及基础横程走廊变化如图9所示,横程及走廊变化如图10所示。

图7 算例2维轨迹图Fig.7 Two dimensional trajectory diagram of Example 2

图8 算例倾侧角变化图Fig.8 Variation diagram of bank angle of examples

图9 算例禁飞区有效映射横程变化图Fig.9 Cross range change diagram of effective mapping of no-fly zones of examples

图10 算例横程走廊变化图Fig.10 Cross range corridor change diagram of examples
从图9中可以看出,飞行器再入滑翔阶段一开始,其瞬时侧向运动轨迹圆便与禁飞区相交,而禁飞区有效映射横程值也比较大,证明其对飞行器未来飞行存在较大影响;通过算例2、算例3的比较,可以看出禁飞区的位置不同,映射横程的叠加结果不同。其叠加结果的值一方面取决于禁飞区与飞行器瞬时侧向运动轨迹圆的相交区域,相交区域越大,禁飞区有效映射横程的值越大,另一方面取决于禁飞区与飞行器、预定目标点的相对位置关系决定的有效映射横程的符号,禁飞区有效映射横程符号相同的,二者相加,且最大值约束在飞行器基础横程走廊最大值,从而影响横程走廊边界值的变化,符号不同的,相加出的结果的正负表示在满足飞行器对不同禁飞区的规避要求和最终制导精度的前提下,自适应横程走廊改变的方向。观察图8和图10可以看出,尽管存在禁飞区,但是通过自适应横程走廊逻辑,飞行器的翻转次数并未增加,并且成功规避禁飞区;飞行器的横程始终位于横程走廊内,走廊边界与横程最终收敛,验证了本文方法的有效性。综上所述,通过本文自适应横程走廊的设计,飞行器横程始终位于走廊内部,可以有效保证横程的收敛。其终端条件及仿真误差如表1所示。表1中飞行器的制导误差用E表示,其计算公式为
(48)
式中:Δφf,Δφf,Δhf分别代表制导经纬度及高度误差。从表1中可以看出,使用本文方法在有禁飞区条件下制导精度均在6 km以内,在自适应横程走廊条件下,横向制导也可实现准确效果。

表1 算例结果
(2) 再入过程扰动仿真
进一步考虑飞行器再入过程受到的大气参数及自身参数变化带来的扰动,验证所提算法对再入过程扰动的鲁棒性,本文考虑大气常数误差(±20%),飞行器质量偏差、受力面积偏差及升阻力系数偏差(±5%)的均匀分布条件下,进行了300次蒙特卡罗仿真。仿真结果如图11所示,大部分结果高度误差小于2 km,平面误差5 km左右,最大不超过10 km。说明在本文制导方法下,其制导精度依然能够满足要求。


图11 飞行器目标位置二维落点图Fig.11 Two-dimensional landing point diagram of aircraft target position
(3) 横向制导及规避方法效果对比
在存在禁飞区情况下,RGV选择的规避距离和侧向制导走廊不同,会产生不同的规避和制导效果。为了体现本文动态引入规避逻辑及自适应横程走廊的优越性,借鉴文献[18]中的禁飞区规避方法,设定飞行器在与禁飞区中心不同距离的情况下,普通的横程走廊制导方式及航迹偏差角走廊制导方式与规避逻辑进行结合,在算例3的初始条件下进行制导,其制导结果如图12和图13所示(注:d为飞行器与禁飞区中心的距离,r为禁飞区半径,其中文献[18]中设定的规避距离为d=2.0r。)。
从图12(a)和图13(a)中可以看出,在与禁飞区中心不同距离加入规避逻辑,规避和制导的效果不同。其中在横程走廊制导下,飞行器都完成了对禁飞区的规避,但在航迹偏差角走廊制导下,当d=1.6r、d=1.7r时加入规避逻辑,飞行器会存在穿越禁飞区,从而规避失败的情况,结果证明横程走廊制导方式对存在禁飞区的规避情况,制导效果更好;从图12(b)和图13(b)中可以看出,在与禁飞区中心不同距离加入规避逻辑,倾侧角的翻转情况不同,因为飞行器的横向制导逻辑与规避逻辑分离,所以当进入禁飞区与制导逻辑的临界状态时,此种规避逻辑容易导致倾侧角反复翻转,使得翻转次数增多。两种横向制导方法与设定的不同规避逻辑相结合的制导误差如表2所示,其中F表示飞行器倾侧角反转次数。

图12 横程走廊加规避逻辑制导方式仿真效果图Fig.12 Simulation effect diagram of lateral corridor with evasion logic guidance mode

图13 航迹偏差角走廊加规避逻辑制导方式仿真效果图Fig.13 Simulation effect diagram of track deviation angle corridor with evasion logic guidance mod

表2 不同制导与规避方式下飞行器制导误差
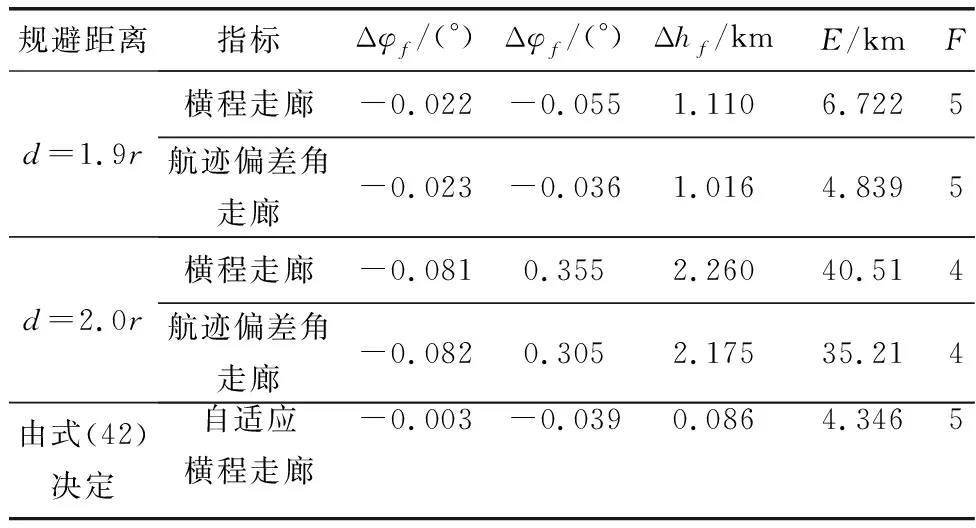
续表2
从图12、图13以及表2中可以看出,在距离禁飞区越近的距离进行规避,其最终制导精度越高,但倾侧角的翻转次数也在增加,同时会存在无法规避禁飞区的情况;在距离禁飞区越远的距离进行规避,其倾侧角的翻转次数明显减少,同时可以成功规避禁飞区,但其制导精度也在急剧下降,很可能会使飞行器无法到达预定目标点,最终导致制导失败;与本文所提的动态引入规避逻辑和自适应横程走廊制导方式对比,因用飞行器的瞬时转弯半径,通过实时判断其瞬时侧向运动轨迹是否与禁飞区相交,来加入规避逻辑,解决了飞行器规避禁飞区的距离选取与最终制导精度之间的矛盾。表2中结果显示,飞行器侧向制导采用本文所提方法,在规避禁飞区后最终制导精度满足要求,并且自适应横程走廊通过将规避逻辑和侧向制导逻辑融合,在保持一定的走廊宽度的情况下,减少了倾侧角的翻转次数。
4 结 论
本文针对RGV预测校正算法中,通常存在禁飞区情况下飞行器横向制导逻辑与禁飞区规避逻辑相分离的情况,通过飞行器瞬时转弯半径,求出瞬时侧向运动轨迹圆,利用该圆与禁飞区相交情况,动态引入规避逻辑,并且把禁飞区对飞行轨迹的影响投影到飞行横程上,提出禁飞区有效映射横程,建立了飞行器的自适应横程走廊。最后仿真结果表明,本文方法不仅针对不同禁飞区情况可以实现有效制导,对再入过程扰动具有一定的鲁棒性,并且与其他制导逻辑相比,在满足制导精度的同时,具有更少的倾侧角翻转次数。

