基于Stacking策略的集成BN网络目标威胁评估
王紫东, 高晓光, 刘晓寒
(西北工业大学电子信息学院, 陕西 西安 710129)
0 引 言
威胁评估属于数据融合模型中的第三级,指的是基于战场实时态势评估作战目标的威胁程度[1]。根据美国空军OODA(observation, orientation, decision, action)环路理论,威胁评估属于决策模块,也是形成体系作战能力的关键一环[2]。针对空海作战任务,必须对威胁评估进行精细化设计,合理地提取威胁要素,动态估算每个打击目标的威胁程度,建立目标的动态威胁队列,为指控人员提供火控打击的决策依据。
目前,针对威胁评估的理论可以大致分为两类,即线性加权法以及非线性推理法[3]。作为一种传统的代数模型,前者主要针对无缺值足量数据,核心思想是由人工确定各个威胁要素在评估过程中的权重,然后通过不同的线性模型进行融合决策。常见算法包括层次分析法[4-5]、粗糙集法[6]、灰关联分析法[7]等。这些方法效率高,但是相应地,其过度依赖专家经验而且无法处理一些离散数据以及缺失数据。后者是近些年伴随着人工智能发展而新兴凸现的理论,核心思想是通过复杂的非线性模型对输入威胁数据进行建模,应用数据挖掘和回归拟合等相关原理,产生威胁评估输出。常见算法包括模糊集[8]、逼近理想解排序法[9]、多准则决策[10-11]等。这些方法具有可扩展性好、能够适应各种类型数据的特点,但是大部分模型都是黑箱模型,可解释性差。
贝叶斯网络作为非线性推理法中的代表算法,是一个白箱模型,不仅可以清晰地表示各威胁因素间的复杂关系,还可以融合专家经验处理不充分数据,使得评估结果更接近于人对威胁评估的认知过程,从而为决策人员提供更多、更合理的备选方案[12-13]。上述优点使得贝叶斯网络方法成为威胁评估中进展最多、发展最快的方法之一:文献[14]提出了一种分层朴素贝叶斯网络进行舰艇对水下不明目标的威胁分析;文献[15]提出一种在数据不充分条件下使用约束最大后验概率进行参数学习的威胁贝叶斯网络模型;文献[16]探索了如何使用动态贝叶斯网络来处理连续不确定性的威胁数据输入;文献[17]则考虑了云模型和贝叶斯网络的融合,解决连续数据下的威胁评估任务;类似地,文献[18]考虑了连续和离散混合数据的贝叶斯网络建模与威胁评估。
可以发现,在威胁评估应用中,贝叶斯网络结构基本都是通过专家手动建立单层或者多层朴素模型,然后通过威胁数据进行参数学习以及推理,鲜有论文尝试探索网络结构本身对于威胁评估结果的影响。然而,单纯依赖专家经验确定的网络结构可能会违背威胁数据背后的客观规律,造成一些不忠实、不准确的条件概率分布表,从而影响推理与威胁评估的精度。
因此,本文旨在探寻一种全新的威胁评估贝叶斯网络建模方法,该方法以基于评分的组合优化结构学习算法为基础,通过威胁数据建立威胁评估网络,同时融合领域专家对于某一想定下的威胁关系先验知识,使得最终模型更加合理。本文称这种模型为集成贝叶斯网络(ensemble Bayesian network, EBN)。本文的主要创新点如下:
(1) 引入基于Stacking的集成学习策略,避免对于特定结构的过度拟合,选取不同搜索空间,包括有向无环图空间、节点序空间以及等价类空间内的评分优化算法,以构建数据观测模型集;
(2) 为了平衡数据学习和专家经验之间的模型差异,采用多数投票机制对于数据观测模型集进行模型平均,采用朴素贝叶斯网络依据不成环规则进行模型微调;
(3) 为了使得最终结构在符合规则的情况下尽可能达到最优,将融合数据观测与专家经验的图模型作为边约束,指导节点序图扩展,通过动态规划算法求取约束下的全局最优网络。
本文还将EBN模型与其他威胁评估模型进行了性能比较。由于引入基于评分最优化的数据观测结构作为约束,因此预期EBN模型评分将会更高;由于融合了专家经验作为结构先验约束,故敏感性分析中EBN也会更加符合常规认知;考虑指定想定下的舰艇编队对于空中目标的威胁评估,由于采用了约束动态规划求取全局最优网络,针对单目标的威胁概率推理,EBN精度预期会高于其他模型,针对多目标的威胁排序,EBN的Spearman系数也会更加稳定且接近真实排序。
1 背 景
1.1 贝叶斯网络基础
贝叶斯网络可以表示为二元组(G,P),其中G代表了网络结构且G=(V,E),G体现为一个有向无环图,V={X1,X2,…,Xn} 代表了网络中的变量集合,E={Xi→Xj|Xi,Xj∈V} 代表了网络中的有向边的集合,形如Xi→Xj的边称Xi是Xj的父节点,记作Xi∈PaG(Xj)。类似地,可以定义子节点Xj∈ChG(Xi)以及祖先节点Xi∈AnsG(Xj)。贝叶斯网络结构学习任务的核心就是在给定数据输入D∈Rm×n的情况下,寻找到一个合适的网络结构G来尽可能地拟合数据中的因果关系。类似地,该问题可以建模为一个约束优化问题[19]:
s.t.Xi∉Ans(Xi), ∀Xi∈V
(1)
式中:F(·) 代表了评估函数,用以描述观测到的结构G与数据D的似然度;而G代表了候选网络空间。基于评分优化的方法,将F(·)具象化为一系列的评分函数score(G|D),例如似然度罚项评分、狄利克雷先验评分等等。这些评分都具有可分解性:
F(G,D)=score(G|D)=
(2)
即整个图的评分是各个节点所在子图的评分之和。在实际计算中,通常会预先把每个节点的父节点集合及其评分计算并存储在评分缓存中,之后在不同的搜索空间中使用启发式搜索算法进行式(1)的求解。常见的搜索空间包括节点序空间[20-21]、有向无环图空间[22-23]以及等价类空间[24]。
1.2 集成学习策略
集成学习是机器学习中常见的模型融合方法,单个学习器易出现对数据的过拟合或者欠拟合,综合多学习器则可解决这一问题。集成学习策略包括Boosting、Bagging以及Stacking[25-26]。本文使用Stacking策略,该策略基于异质基学习器,分批次学习到不同模型并最终使用元学习器进行模型融合,如图1所示。该策略实现过程如下。
步骤 1针对输入数据D∈Rm×n,其中n代表了数据输入维度,m代表了数据条目数,依据基学习器个数生成p份数据:
(3)
式中:[·]i代表矩阵第i列所有数据。根据p折交叉检验原理,则输入到第q个基学习器的数据集Dq为
(4)
步骤 2设不同基学习器的框架为G=fk(·),则经过初次学习获得的模型可以表示为
(5)
步骤 3设元学习器框架为G=F(·),则最终的输出模型可以表示为Go=F(G)。

图1 基于Stacking策略的集成学习Fig.1 Ensemble learning based on Stacking strategy
2 基于Stacking的EBN建模
基于Stacking的EBN构建以3个数据观测模型作为基学习器,如图2所示,以专家经验的模型融合与模型求解作为元学习器,具体包含以下3个步骤。
步骤 1数据观测模型构建:选取3个不同搜索空间(序空间、有向无环图空间以及等价类空间)内的评分优化算法来提取威胁数据中的网络结构;
步骤 2模型融合:包含模型平均与模型微调两部分,前者对于数据观测模型集通过多数投票与阈值化操作获得平均网络,后者通过专家经验朴素模型进行平均网络的边删除与增加;
步骤 3约束动态规划求解器:以获得的平均网络作为威胁约束集合,通过各威胁要素之间的父子关系指导节点序图的扩展,删除非法节点,以动态规划算法求取约束下的最优威胁评估网络。
2.1 数据观测模型建立
(1) 有向无环图空间搜索
有向无环图空间即为贝叶斯网络的原始空间,在该空间中的组合优化算法需要针对每一个节点Xi,寻找最优的父集合Pa(Xi)且满足组成的贝叶斯网络G是有向无环图。这是一个非确定性多项式(non-deterministic polynomia, NP)难问题,因此本文使用启发式算法近似求解其最优解。
步骤 1确定初始解,一般为空图G;
步骤 2使用启发式算子进行图搜索,常用算子包括增边、删边以及转边,如图3所示。
对于步骤1中确定的网络结构G,随机使用上述3种操作算子得到新图G′,如果满足score(G|D) 步骤 3针对步骤2中获取的局部最优解,使用迭代重启获取新的搜索图,重复进行步骤2,直至满足迭代停止条件。 (2) 节点序空间搜索 节点序空间由一系列的节点序p构成,节点序p={X1,X2,…,Xn}中的变量Xi满足PaGXi⊆{Y∈V|IY (6) 因此,根据式(6)寻找评分最高的结构,可等价为寻找评分最高的节点序。其具体步骤如下。 步骤 1获取随机的初始节点序p; 步骤 2使用搜索算子如insertion, windows, swap[19]等对当前节点序p进行操作以获得其邻居节点序p′,本文默认使用insertion算子。 步骤 3重复步骤2至score(p′|D)≤score(p|D)成立,则认为达到了局部最优结构,需要进行迭代重启来获得新的节点序。 步骤 4反复进行步骤3直至达到规定的终止条件,使用式(6)来获取当前p′所对应的最优网络结构G。 (3) 等价类空间搜索 等价类空间是有向无环图空间的精简,对于一系列有向无环图G1,G2,…满足拥有相同的骨架和v-结构,则称其为一个等价类P,同一个等价类内的所有结构拥有相同的评分,在该空间内的启发式搜索步骤如下。 步骤 1初始化获得一个空的图Pold; 步骤 2执行前向等价搜索(forward equivalence search, FES),该过程中,遵循不成环规则确定可增边的集合,然后针对集合内变量使用操作算子Insert(Xi,Xj,T)增加Xi与Xj之间的边,并且对T内的变量进行定向操作以确保Pnew仍然为一个部分有向无环图; 步骤 3执行后向等价搜索(backward equivalence search, BES),该过程与步骤2类似,不同的是使用了Delete(Xi,Xj,T)算子来对步骤2中的局部最优结果进行删边操作; 步骤 4交替执行步骤2与步骤3直至score(Pnew|D)≤score(Pold|D)。 上述3个模型均为基于评分学习贝叶斯网络结构的组合优化算法,构成了集成学习的基学习器,而本文也设计了一种模型融合方法来进行元学习器的学习,具体包括模型平均与模型微调。 图2 基于Stacking策略的集成贝叶斯网络构建框架Fig.2 Ensemble Bayesian network construction framework based on Stacking strategy 图3 图操作算子Fig.3 Operators for graph search (1) 模型平均 针对数据观测模型集,计算平均网络结构Wf: (7) 式中:Wi代表第i个基学习器贝叶斯网络模型对应的权重矩阵,[Wi]jk=1代表了模型Gi内存在边Xj→Xk。模型平均时的核心决策遵循为:如果超过半数的模型中均存在Xj→Xk,则默认最终模型Wf中也存在该边。 为了将权重矩阵二值化,需要引入阈值函数Thres (·),如果Wf中Xj→Xk的权重不小于1,即满足上述规则,则认为最终模型中存在该边,反之如果该边权重小于1,则需要将该边从最终模型中删除。最后将Wf投影到有向无环图空间,得到模型平均贝叶斯网络结构Gf。 (2) 模型微调 在获得观测数据平均模型Gf后,考虑与专家经验模型的融合,对于任意的朴素多层贝叶斯模型Gn,如图4所示。 图4 多层朴素贝叶斯网络Fig.4 Mult-layer naive Bayesian network 遵循有向无环约束,则Gf与Gn融合生成的网络Ginc中的边需要满足以下微调规则: ① 如果Xj→Xk∈Gn且Xj→Xk∈Gf,则Ginc保留该边; (8) 式中:{Xj,Xj+1,…,Xk}代表了Gf与Gn中由于成环而冲突的变量集合。若式(8)成立,则认为Gf中的结构更加合理,Ginc选择该子结构;反之若式(8)不成立,则选择Gn中对应的子结构。 动态规划将贝叶斯网络的结构学习问题转化为一系列子问题,针对任意的节点Xi,有 Score(V)=Score(VXi)+BestScore(Xi,VXi) (9) 式(9)成立。其中: BestScore(Xi,VXi)= (10) 若Xi固定为叶节点(即Xi无后代节点),剩余的变量VXi会形成一个最优的子网络,且Xi的最优父集合PaG(Xi)可从该子网络中发现。因此,最优的贝叶斯网络结构G可以通过比较每个Xi∈V,i=1,2,…,n成为叶节点而实现,即 BestScore(Xi,VXi)} (11) 式(11)表明了动态规划学习贝叶斯网络的基本原理,通过式(11)可以把学习分解为多个独立的阶段,每一个阶段的实现需要如下过程。 (1) 从任意一个图Gold开始,随机地将一个节点Xi当做叶节点加入图中形成Gnew; (2)Xi的最优父节点集合PaG(Xi)从Gold所有的变量Uold中获取,并将PaG(Xi)→Xi加入到Gnew中,将Gnew视为Gold; 从一个空图开始,反复进行上述步骤直至所有的节点被遍历完毕(Uold=V),即可完成搜索。但是,单次遍历只会得到一个解。因此,需要对于所有的子集执行上述过程,由此形成的搜索图称为节点序图,在节点序图中进行搜索将得到全局最优解。图5展示了一个4节点的节点序图。 图5 4节点的节点序图Fig.5 Order graph of four nodes 然而,计算该搜索图的复杂度为O(2n),仅适用于小规模网络,为了能够达到威胁评估所需要的网络规模,本文提出了融合专家经验和数据观测的网络Ginc,形成约束集,化简节点序图的搜索过程: 考虑Ginc中某条约束边X1→X2,节点序图中{X2}由于违反了约束而成为一个非法节点,则包含该子结构的后续节点均是非法的。但是非法节点的后代也可能是合法的,因为其可能是通过其他合法节点遵循着约束扩展而来的。鉴于这种复杂的情况,本文提出了如下的删减节点序图的方法: 算法 1 定理 1算法1生成的节点序图中,所有存在的节点都满足约束Ginc,而所有被删除的节点都违反了约束Ginc。 证明可以使用数学归纳法来证明。 步骤 1如果考虑节点为空集,必然是满足约束集Ginc的,因为初始阶段未删除变量。 步骤 2当节点Uold被扩展时,假定此时节点序图中所有存在的节点都满足约束集Ginc而所有被删除节点都违背约束集。现证明通过算法1扩展的节点仍然满足约束集Ginc,新删除的节点则不满足约束集。 证毕 待所有节点扩展完成后,得到最终的威胁评估EBN,后续进行网络的参数学习和推理,即可实现威胁评估的闭环应用。 想定以红方舰艇编队针对蓝方组织的反舰攻击展开防空作战为背景。红方编队由5艘水面舰艇组成,蓝方作战力量由4组飞行编队组成。在整个作战过程中,红方保持编队阵型不变,以旗舰为编队中心;蓝方飞行编队将从距红方编队中心约200 km的不同方向发动进攻。蓝方编队包括2组舰载攻击机、1组电子战攻击机以及1组无人侦查机(攻击机用于对海作战,电子攻击机用于电子压制作战,无人侦察机用于电子侦查作战)。每次推演中,蓝方发动进攻的方向均会发生改变。 由于蓝方电子压制的原因,红方对蓝方的探测受到干扰,无法获取蓝方准确信息。为了反映探测的不确定性,同时为了满足真实威胁程度的计算,每一条数据由两部分组成,分别是探测数据、真实数据。探测字段代表了红方传感器对目标的探测结果,由于蓝方的干扰,存在数据项的缺失以及探测结果的不准确;真实字段代表了从上帝视角看到的蓝方单位精确信息。各字段的说明如表1所示。 表1 威胁数据字段说明 对于威胁数据进行清洗,剔除掉无效数据、缺失数据等。将探测字段的11个属性作为目标的探测属性,对于真实字段,选取了目标类型以及目标状态属性作为中间变量,最后将威胁等级和到达时间作为最终的观测变量,构建贝叶斯网络。其中,威胁等级和到达时间的确定方式如下。 威胁等级是由目标状态和目标类型直接决定的,具体规则为:电子侦查机恒定为低危目标,战斗机恒定为中危目标,电子攻击机以及所有反舰导弹恒定为高危目标。当飞行编队执行任务结束时,战斗机降为低危目标,电子攻击机降为中危目标。到达时间的计算方法为g([f(Tlon,Tlat,Talt)]-[f(Slon,Slat,0)])/Tsp。其中,Tlon,Tlat,Talt代表了目标的经度、纬度以及高度;Slon,Slat代表了红方旗舰经度与纬度位置;f(·)为经纬高与局部地理坐标系转换函数;g(·)为距离计算函数;Tsp为进行换算后的目标速度。以上变量均采用真实字段的数据。类似地,在后续表示过程中也使用了经度差、纬度差以及高度差的概念来代替初始目标的经纬高,以期望更好地表达仿真数据中红蓝双方位置相对关系这一概念。 因此,基于探测字段与真实字段,获得了共计15个节点用于威胁评估与威胁推理,其中连续变量共计9个,而为了后续运用于贝叶斯网络结构构建,需要对其进行离散化。对于到达时间、经纬高差、速度以及距离,采用了等频率的离散化方法,针对某一变量X的实例取值x落入到分类区间[bi,bi+1]的条件为 (12) 式中:DX为按增序排列后的关于X的数据集;m为初始数据集的数目;q为对于X的离散化区间数,此处统一设置为5。对于进入角、探测时间以及探测间隔则采用了等分点划分方式。类似地,针对某一变量X的实例取值x落入到分类区间[bi,bi+1]的条件为 (13) 表2 威胁数据状态以及离散化结果 通过数据学习贝叶斯网络进行威胁评估的过程如图6所示。 图6 基于贝叶斯网络的威胁评估流程Fig.6 Threat assessment process based on Bayesian network 基于贝叶斯网络进行威胁评估的主要流程包括4部分,即数据获取与离散化、结构学习、参数学习以及威胁推理。第1部分在第3.1节已经实现,第2部分则为本文第2节所关注的重点问题,使用了基于Stacking的EBN构建方法,将3种不同空间的结构学习算法作为基学习器(第2.1节),融合专家经验确定朴素网络(第2.2节),生成一些约束并以此指导元学习器(动态规划算法,第2.3节)来构筑最终的威胁评估网络,最终的学习结果如图7所示。 图7 EBN学习到的威胁评估网络Fig.7 Threat assessment network learned by EBN 图7表示了根据威胁数据学习到的EBN结构。对于数据分布中体现的目标类型与威胁等级、目标状态与威胁等级等的因果关系,EBN均能够观测到对应边。到达时间是由多个因素共同决定的,诸如速度、经纬高差、距离等,EBN亦可发掘这些关系。由于有向无环的约束,多条边(到达时间与距离等)都出现了反向,这种情况在其他模型中也很常见。此外,为了追求网络性能以及推理效果,部分观测节点之间出现了复杂的相关关联。 本节也对EBN进行了敏感性分析。敏感性分析表示威胁评估模型中各威胁要素对于最终威胁等级与到达时间的影响程度。选取了预期方差的减少比例VR、互信息的减少比例MI作为评价指标,该数数值越大,说明威胁因素的影响力越强。此外,将目标节点自身的初始值设置为标准值,可求取其他威胁要素的百分比数值。在EBN中,对威胁等级与到达时间节点的敏感性分析结果如表3和表4所示。 表4 EBN模型针对到达时间的敏感性分析 从表3中可以发现,目标类型和目标状态都会对威胁等级产生较大的影响,这与专家经验相吻合。对应地,EBN则将其设置为威胁等级的父节点。进入角的观测可能会造成较大的方差偏移(73%)和较小的互信息偏移(25.9%)。其他节点对威胁等级的影响大致可以划分为两类:一是间接影响威胁等级的节点,按影响等级从大到小排序为距离、到达时间、经纬高差等,这些节点对威胁等级的影响介于20%~50%之间;二是一些几乎没有影响的节点,诸如传感器、探测间隔、辐射源、探测时间以及电磁辐射等,这些节点的VR与MI普遍低于20%。 正如专家经验所期望,表4中影响到达时间最甚的两个节点为速度和距离。由于不同飞行器速度不同,目标类型会极大地影响到达时间,而传感器的探测结果也属于目标类型的间接体现。由于威胁等级与目标类型密切联系,分析结果表明其与到达时间亦相关,经纬高差则是距离的另外一种表现方式。上述这些节点都可间接影响到达时间的状态,MI与VR较高。剩余的一些节点则对于到达时间的影响程度较小,如进入角、目标状态等。 本文的对比模型选取了朴素贝叶斯网络模型、因果模型、连续优化模型以及组合优化模型,后三者分别使用了PC (Peter and Clark)算法[27]、有向循环图图形神经网络(directed acyclic graph graphical neural network, DAG-GNN)[28-29]算法、HC(Hill Climbing)算法[30]来构建。比较标准为不同模型的似然度罚项评分[19],该评分越高,代表模型与数据的拟合程度越好。其中,表5与表6分别展示了这些模型在标准数据集[31](数据量为1 000)以及本次仿真的威胁评估数据集上的评分结果。 表5 标准数据集评分比较 表6 威胁评估数据集评分比较 N代表了不同数据集的变量数,由于标准数据集没有朴素网络结构,故此处不列出其对比结果。从表5可以发现,EBN在4/5组实验中取得最好的评分结果,而HC评分次之,在两组中表现最好,且在其他组中与EBN相差不大。反观DAG-GNN与PC模型的评分比前二者差一些。由此说明了EBN模型从离散数据中学习网络结构的优越性。 从表6可以发现,EBN仍然取得了最好的效果,PC由于只学习到了少量的边,因此其评分是最低的,朴素贝叶斯网络模型则因为人工定边违背数据分布规律,故其评分效果也较差。DAG-GNN在处理连续数据时有着出色的效果,但是针对离散数据,其表现略有下降。组合优化模型HC则获得了较高的评分,而EBN模型由于引入动态规划与模型平均,可精确地拟合数据,寻找到全局最优解,因此其评分最高。 所有模型均使用最大似然估计[30]算法进行参数学习,后续依据红方传感器获取到的探测数据,使用联接树算法[19]推理获取威胁等级与到达时间。由于推理结果为概率分布,为了方便比较,本节实验使用单个目标真实状态的推理概率与全概率(即1)之间的差异作为指标,该概率差异越小,说明推理结果越接近真实状态。此外,本文还模拟了真实战场环境中可能出现的证据获取不足的情况,使用了1、5、11个观测节点进行威胁推理。每组实验均重复20次,每次随机选取证据的取值状态,以概率差异的平均值来衡量模型的威胁评估性能。 在获取单个观测节点时,不同模型的到达时间和威胁等级的推理概率差异如表7所示,其中每组的最小值被加粗。针对威胁等级,朴素贝叶斯模型与HC模型均在4/11组实验中得到最小的推理差异,EBN在7/11组实验中推理差异表现最好,而DAG-GNN模型以及PC模型在所有证据下均与真实的威胁等级差异较大。此外,由于HC模型使用了基于评分的策略,其推理精度与EBN相差甚小,二者均保持在0.3左右(此时推理的威胁等级正确率为70%,可以帮助指控人员做出正确的决策)。针对到达时间,朴素贝叶斯模型、EBN模型以HC模型均取得了较好的结果,分别在3组、5组以及6组实验中达到了最小概率差异,PC与DAG-GNN表现仍然很差。所有模型概率差异整体基数较大,即使是表现最好的HC模型与EBN模型,也仅在查询到速度时才会达到0.56左右的正确率,在其他情况下正确率均低于0.5,因此在获悉单证据时对于到达时间的推理,所有模型表现可信度较差。 表7 单组证据下不同模型对于威胁等级与到达时间的推理概率差异 随机选取11组证据时,不同模型对威胁等级以及到达时间的推理结果如表8所示,每组证据均随机设置5个观测节点,6个缺值状态,每组实验中的最小值被加粗。针对威胁等级,在所有的11组实验中,EBN均获得最小的推理概率差异,按照推理差异的均值排序,不同模型性能为:EBN>HC>朴素贝叶斯网络>DAG-GNN>PC, 对应值分别为0.142、0.160、0.254、0.255以及0.370。针对到达时间,EBN在9/11组实验中取得最低的推理差异,其次为HC模型,其在2组实验中表现最好,且在其他组实验中与EBN差距很小。横向对比单观测节点推理的情况,多观测节点推理的精度有了很大程度的提升。由于获悉更多证据,EBN在所有情况下推理真实状态的概率均超过50%,但是朴素贝叶斯模型只在6组实验中推理真实状态的概率超过50%,其威胁评估结果不一定可信。在获得更多证据时,连续优化模型的评估效果有一些精进,而因果模型结构过于简单,此时的推理结果仍然不尽人意。 在已知所有11个节点取值的情况下,不同模型的威胁评估结果如表9所示。此时,EBN仍然有着最好的推理效果,针对威胁等级,其精度高达97.4%,高于常用的朴素贝叶斯模型(87.9%)。针对到达时间,EBN的精度达到了81.9%,亦高于朴素贝叶斯模型(74.3%)。因此可以断定,在全证据时,EBN模型相较于其他模型在单目标威胁决策中有着更好的表现。 表9 全证据下不同模型对于威胁等级与到达时间的推理概率差 本节考虑不同模型在红方飞行编队的威胁评估与威胁排序中的表现。编队内部不同飞行器(共计q架)的威胁指数计算方法如下: (14) (15) 该系数越大,说明两个排序越接近。类似于第3.4节实验,本节仍然考虑探测数据获取不全面的情况(对应已知1、5、11个观测节点),设置蓝方飞行编队内飞行器个数为20,且每次排序实验都会随机采样20组数据获取Spearman系数分布。 图8展示了获取单观测节点时,不同模型计算的威胁排序与真实威胁排序之间的Spearman系数分布。由于因果模型表现太差,Spearman系数稳定在0左右,因此并未被列入图中的比较。可以发现,除了获取距离之外,其他单组证据下所有模型的威胁排序结果并不理想,中位数均分布在0.8以下,在最差的情况下,诸如获得辐射源信息之后,最高Spearman系数只有0.55。针对不同模型之间,EBN在获得纬度差、距离、传感器信息以及辐射源信息作为证据时,其分布中位数高于其他模型,HC模型则在5组实验中获得了最好的Spearman分布。朴素贝叶斯网络模型的优势在于其鲁棒性好,分布稳定,但是其总体的数值偏小,不如前二者。最后,DAG-GNN模型的结果浮动较大,比如在已知速度或者纬度差的情况下,该模型与其他模型的结果严重偏离,但在剩余情况中,则与其他模型结果相近。 图8 不同模型在单观测节点下的20组目标威胁排序Spearman系数分布Fig.8 Spearman coefficient distribution of 20 sets of target threat ranking for different models under a single observation node 图9展示了在已知5个观测节点的情况下,不同模型在随机11组证据中的威胁排序Spearman系数分布。随着获得的证据增多,EBN的优势开始凸显,在11组实验中,EBN均取得最高的分布中位线,而且除证据组10以外,其他结果箱体普遍很窄,表现稳定。其他3个模型之间的威胁排序效果较难区分,如DAG-GNN在证据组7、3中比HC好,但是在其他证据组中比HC差。而朴素贝叶斯网络模型的排序结果在证据组7、3、4、6中均为最差,但在其他证据组中比DAG-GNN表现更好。 图9 不同模型在5组观测节点下的20组目标威胁排序Spearman系数分布Fig.9 Spearman coefficient distribution of 20 sets of target threat ranking under five sets of test nodes from different models 图10展示了全证据情况下,不同模型的威胁排序结果,箱线图内部的点表示了20组随机样本的具体Spearman数值。由图10可以发现,EBN的威胁排序分布最为优秀,大部分结果落在0.975,其Spearman最大值亦高于其他模型,最小值为0.962 5左右,与HC模型的平均值以及朴素贝叶斯网络模型的最大值水平相当。因此,在实际多目标威胁排序任务中,如果数据量充足,EBN模型效果要比专家经验模型效果更好。 图10 不同模型在11组观测节点下的20组目标威胁 排序Spearman系数分布Fig.10 Spearman coefficient distribution of 20 sets of target threat ranking under eleven sets of test nodes from different models 此外,本节还探究了编队目标数目变化的情况下不同模型威胁排序性能,具体结果如图11所示。由图11可以发现,在目标数目较少(<50)时,朴素贝叶斯网络与HC模型都可精准预测正确的威胁排序,但是随着目标的增多,Spearman系数略有下降(从0.98到0.95)。而EBN模型无论针对少量目标,还是大量目标,其Spearman系数始终维持在0.975之上。综合威胁排序性能如下:EBN>HC>朴素贝叶斯网络>DAG-GNN>PC。 图11 编队目标数目变化时不同模型威胁排序Spearman系数Fig.11 Spearman coefficient of threat ranking in different models with the variation of number of targets 本文提出基于Stacking的集成学习策略构建EBN模型,同时考虑数据观测模型和专家经验模型,通过模型平均和模型微调获得边约束集合,指导动态规划获取约束下的全局最优网络,将其运用到舰艇防空威胁评估任务中,可以发现: (1) EBN结构的BDeu评分与BIC评分较其他模型更高; (2) 对EBN敏感性分析的结果显示,网络结构涵盖了专家对于特定想定下的一些威胁要素关系的认知; (3) 在单目标威胁概率推理任务中,针对观测节点缺失与完整的情况,EBN正确推理威胁等级与到达时间的状态概率均高于朴素贝叶斯模型10%。 (4) 在多目标威胁排序任务中,针对观测节点缺失与完整的情况,EBN展示的排序Spearman系数分布均优于传统的朴素贝叶斯模型。 然而,本文的模型仍然存在着不足之处,其精确求解全局最优结构的效率可能不及朴素贝叶斯模型与其他结构学习模型。未来的研究方向主要集中在如何进一步提高EBN建模效率,使之可以适应真实战场环境下的威胁评估。2.2 模型融合






2.3 约束动态规划求解器





3 仿真实验
3.1 仿真数据

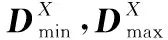

3.2 网络学习结果



3.3 网络性能比较


3.4 单目标威胁评估
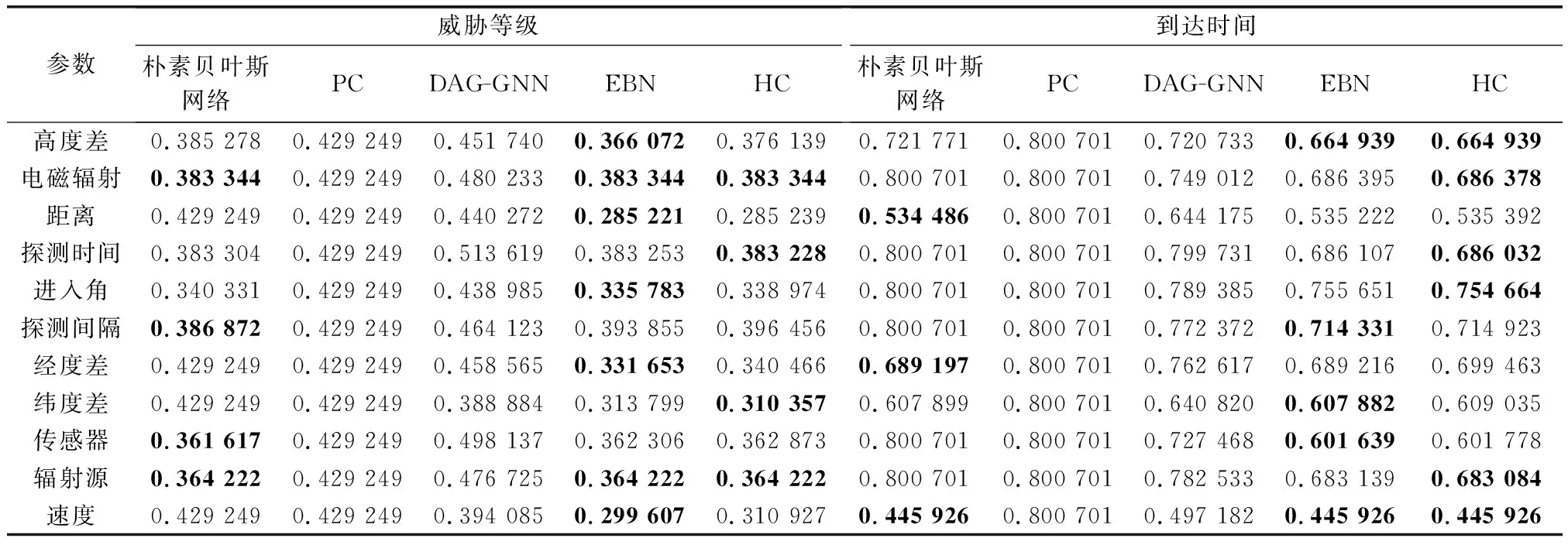

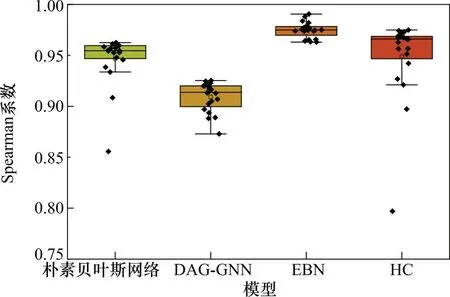
3.5 多目标威胁评估


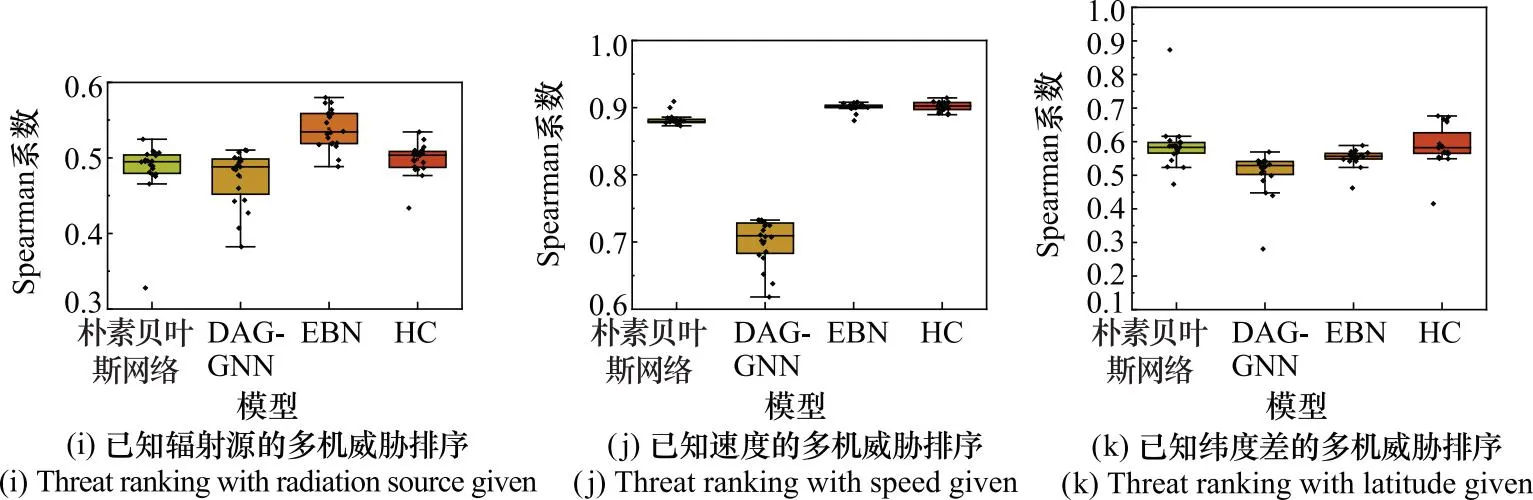
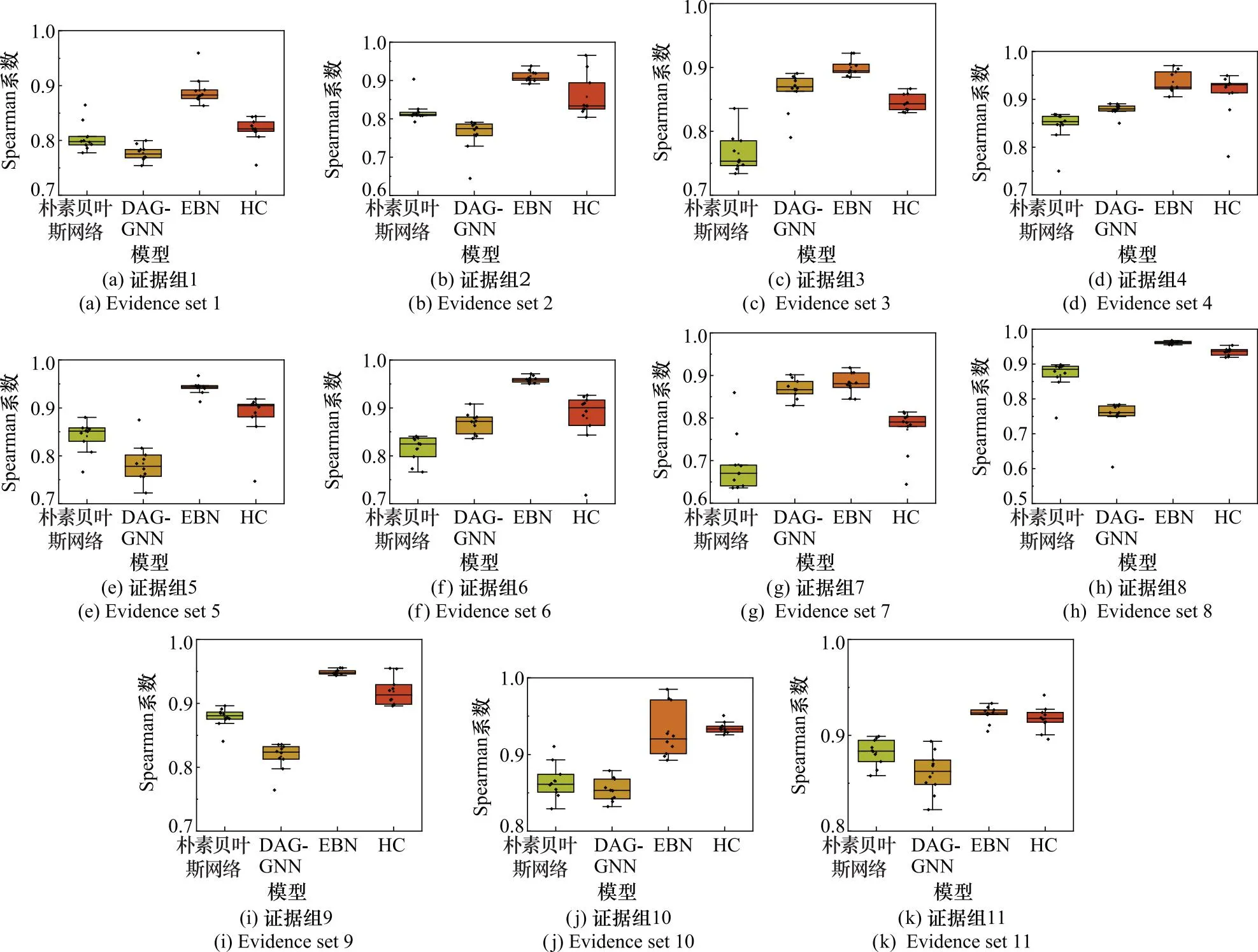

4 结束语

